隧道爆破振动影响因素模拟分析

陈清松 崔 硕 李小青

(广东省南粤交通揭惠高速公路管理中心1) 揭阳 515325) (中交第二公路勘察设计研究院有限公司2) 武汉 430000) (华中科技大学土木工程与力学学院3) 武汉 430074)

0 引 言

小北山1号隧道分左线、右线布置，左线隧道里程ZK14+390～ZK17+386，长2 996 m，最大埋深286.66 m；右线隧道里程K14+380～K17+384，长3 004 m，最大理深268.6 m.

本文结合小北山1号隧道工程爆破施工，进行爆破振动测试试验研究.使用爆轰波的C-J理论和应力波衰减规律进行小北山1号隧道爆破荷载的计算.分析影响爆破振动的相关因素，在此基础上重点分析段间隔时间对减振爆破的影响；对不同间距的先后行隧道的振速特征进行分析研究.

1 小北山1号隧道爆破振动简化爆破荷载的确定

1.1 爆炸荷载

Lu等[1-2]通过理论分析和数值模拟，依据凝聚炸药爆轰波的Chapman-Jouguet理论，绘制出图1的爆炸荷载时程曲线，将其简化为三角形荷载.图1中：Pb0为爆炸荷载峰值；tr为上升时间；tb为正压作用时间.

图1 爆炸荷载时间历程图

耦合装药条件下的炮孔爆炸荷载峰值Pb0为

(1)

式中：ρ0为炸药密度；D为炸药爆速；γ为炸药的等熵系数，一般取3.0.

对于径向和轴向都是不耦合装药的掘进眼和周边眼，炮孔壁的初始冲击波荷载峰值为

(2)

式中：dc为装药直径；db为炮孔直径；lc为药卷直径；lb为炮孔直径；γ为炸药的等熵系数，一般取3.0.

1.2 等效边界

依据岩体的破坏程度，炮孔周围岩体可划分为粉碎区、破碎区和弹性振动区.将非弹性区(粉碎区和破碎区)等效为爆炸源以便于使用弹性本构关系，并将爆炸荷载作用在此等效弹性边界上.

王明洋等[3]对爆炸近区速度场的分析得出，球形装药条件下非弹性区半径γd为

(3)

式中：ρr为岩体的密度；cp为纵波波速；σc为岩石单轴抗压强度.

在掏槽眼爆破时其临空面较少，受到的夹制作用相对较强，而除掏槽眼外其他各段炮孔起爆时临空面条件都较好，从而在确定等效作用边界时需分掏槽眼和非掏槽眼两种情况进行.若将各炮孔间的互相作用忽视不计，那么每一个掏槽眼爆炸都可类比于柱状炸药在半无限介质中的爆炸.

掏槽段各炮孔爆炸时所造成的破碎区的包络线即可视为等效弹性边界，见图2.在柱状装药条件下装药半径的3～5倍范围可视为粉碎区，装药半径的10～15倍范围可视为破碎区半径.

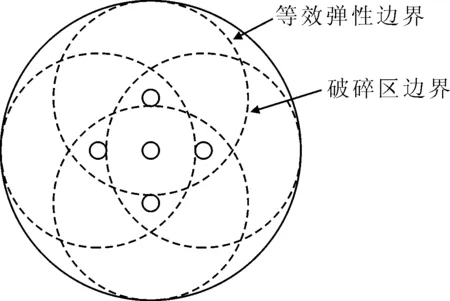
图2 掏槽眼等效荷载作用边界图

掏槽眼起爆给随后起爆的掘进眼创造了临空面条件，各圈掘进眼、周边眼都是在临空面条件较好的情况下，依靠各圈炮眼爆炸产生裂缝及相邻炮眼产生的裂缝互相连通来完成对拟爆破岩体的崩落和抛掷的，从而掘进眼和周边眼爆破时的等效弹性边界可以近似看做是新产生的自由面.

1.3 等效边界上的荷载

单一炮孔爆炸时爆炸应力波在爆源近区依距爆源远近按幂函数的规律进行减弱[4].设任一时刻炮孔壁上的爆炸荷载为Pb(t)，那么多个同时起爆的掏槽眼等效到其弹性边界上的爆炸荷载Pbe(t)为

(4)

式中：k为多个掏槽眼起爆时的荷载影响系数；r0为炮孔半径；r1为粉碎区半径；r2为破碎区半径；μ为岩石泊松比.

按照多炮孔同时爆破时应力波叠加的概念，k值的主要用途是将应力波叠加效应考虑进来，这样便可以将多个掏槽眼的应力波进行一定程度的叠加作用后施加在等效弹性边界上[5].所以，k值为

(5)

式中：n为掏槽眼的个数；re为掏槽眼等效弹性边界的半径.

式(5)为掏槽眼群孔起爆时所各自形成的破碎区面积之和与整体等效弹性边界面积的比，也可以表示为图2中所有虚线圆面积之和与实线大圆面积的比.

在圆形隧道条件下，非掏槽眼起爆时将炮孔壁上的爆炸荷载作用在同段位各炮孔中心连线与炮孔轴线所定的平面上：

(6)

式中：S为两临近炮孔间的距离.

因为非圆形隧道的各炮孔之间的距离S是有所变化的，也即S不是常量，所以在对非掏槽眼的Pbe(t)进行计算时不能按照上式(6)进行.基于静力平衡和圣维南原理，利用周长等效的方式将Pbe(t)作用在相同段位各个非掏槽眼连心线所形成的等效弹性边界上，以此来去除S值的影响，见图3.非掏槽眼等效弹性边界处爆破峰值荷载Pb0为

(7)

式中：n为非掏槽眼的个数；r0为非掏槽眼的半径；为非掏槽眼连心线围成的等效弹性边界长度.

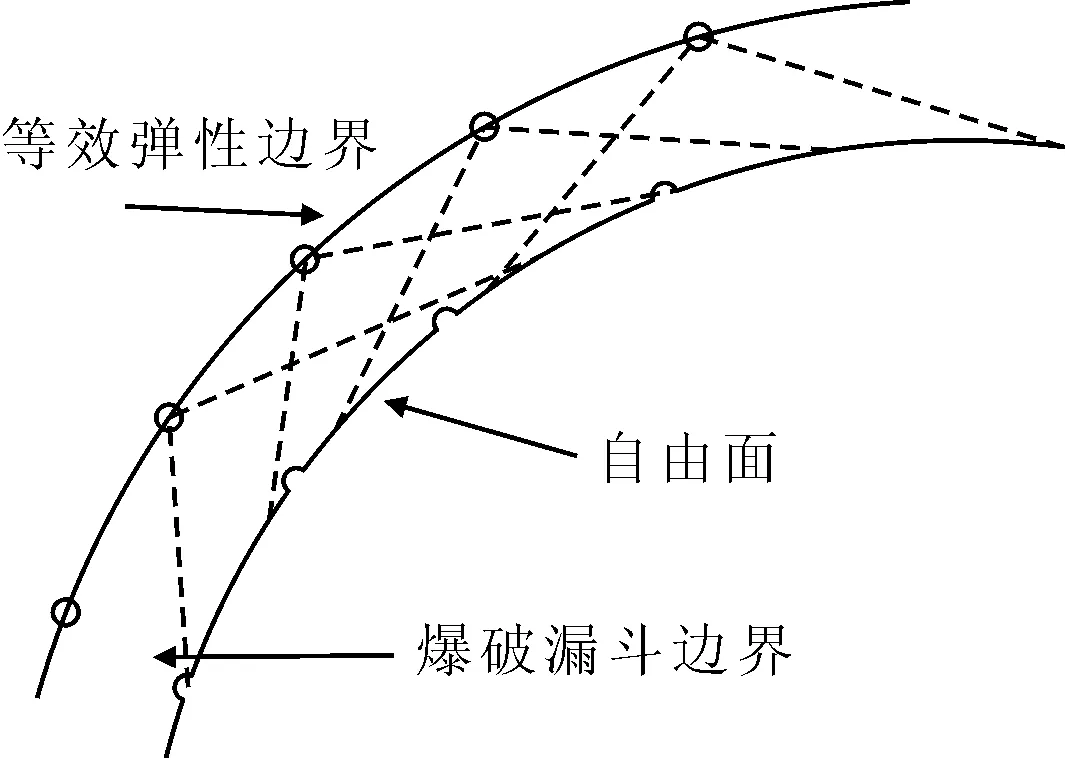
图3 非掏槽眼等效荷载作用边界图

在式(7)中仅计算了非掏槽眼炮孔的半个周长，这是因为可以大致认为对炮孔周围围岩以及支护结构造成危害的只是残余的炮痕部分传递过来的爆破荷载，另外一半的爆破荷载是作用在破碎及抛掷掌子面岩石上，并没有对围岩和支护结构造成危害.

1.4 隧道开挖轮廓面上的荷载

依据应力波的衰减规律，将等效边界上的荷载逐渐衰减后施加在开挖轮廓面上,从而得出开挖轮廓面上的等效荷载和对比距离计算式

(8)

(9)

式中：rb为开挖轮廓的半径；re为等效边界的半径；α为应力衰减指数.

岩石泊松比与应力衰减指数之间的经验关系为

(10)

式中：μ为泊松比.

对式(9)中的r进行计算时，将等效弹性边界或开挖轮廓边界大致看作圆形，圆心选做上述边界所围成面积的质心，则此圆形的半径为

(11)

式中：rε为等效边界半径；A为等效边界或开挖轮廓所围成的面积.

1.5 爆破荷载作用时间

较常使用的三角形爆炸荷载加载和卸载时间的计算公式为

(12)

(13)

式中：K为围岩的体积压缩模量，MPa；Q为炮眼装药量，kg；r为对比距离，m；u为岩石泊松比.

1.6 小北山1号隧道上台阶开挖爆破荷载计算

采用上述爆破荷载简化计算方法并根据小北山1号隧道爆破参数，对小北山1号隧道上台阶开挖爆破不同段位的等效爆破荷载进行计算，见表1.

表1 小北山1号隧道上台阶爆破荷载计算表

将上述表格计算所得的峰值荷载、加载时间等结合毫秒雷管段位绘制出爆破荷载曲线图，见图4.

图4 小北山1号隧道上台阶爆破荷载时程曲线

2 隧道爆破振动不同影响因素模拟分析

2.1 爆破荷载不同段间隔时间对振速的影响

在选用的炸药确定的情况下，单段炸药量大小、微差间隔时间对振动速度有较大的影响.随着单段炸药量的增大，振动速度是随之增大的，而间隔时间的影响却无法简单地表现出来.

选用图4小北山1号隧道上下台阶法爆破荷载时程曲线的第九段和第十一段荷载，依次改变其间隔时间为15，25，50，100和200 ms，分析对比在不同的微差时间下，隧道的振动速度特征的变化.

2.1.1沿隧道轴向振速分布分析

在隧道轴向掌子面前方每3 m选取一个截面，在各个截面选择4个关键点，依次位于拱顶、两侧拱腰和拱底.提取各关键点的横向(Vxmax)、纵向(Vymax)和竖向(Vzmax)的振动速度峰值，绘制成折线图.

图5为拱顶位置沿隧道轴向振速分布图.左拱腰、右拱腰、拱底位置沿隧道轴向振速分布图同理可知，限于篇幅，此处略.

图5 拱顶位置沿隧道轴向振速分布图

由图5可知，①随着延时的增加，在15 m范围内，拱顶位置的横向振速峰值逐渐降低.延时15 ms爆破荷载产生的横向振速最大峰值是数值最小的延时200 ms的154.0%.随着距离的增加，不同延时之间的振速峰值差距逐渐减小.②在30 m距离范围内，延时15和25 ms的同一观测点的纵向振速峰值交替领先，并与其他组数据有较大的差距.延时15 ms的纵向振速最大峰值是数值最小的延时50 ms的131.2%.③竖向振速峰值在10 m之后差距就比较小，在10 m范围内延时25 ms的振速峰值最大，是数值最小的延时200 ms振速峰值的158.6%.④综合对比三向振速特征，在拱顶位置延时15和25 ms产生的振速峰值较大，一般是其他延时产生的振速峰值的120%以上.

2.1.2截面峰值振速分布规律分析

取爆心距R=4.0、10.0、19.0 m处的截面峰值振速，作隧道截面上横向(x方向)、纵向(y方向)、竖向(z方向)的峰值振速分布图，见图6～8(图中均使用极坐标系，坐标原点为隧道轮廓的中心).

图6 R=4.0 m截面峰值振速分布图

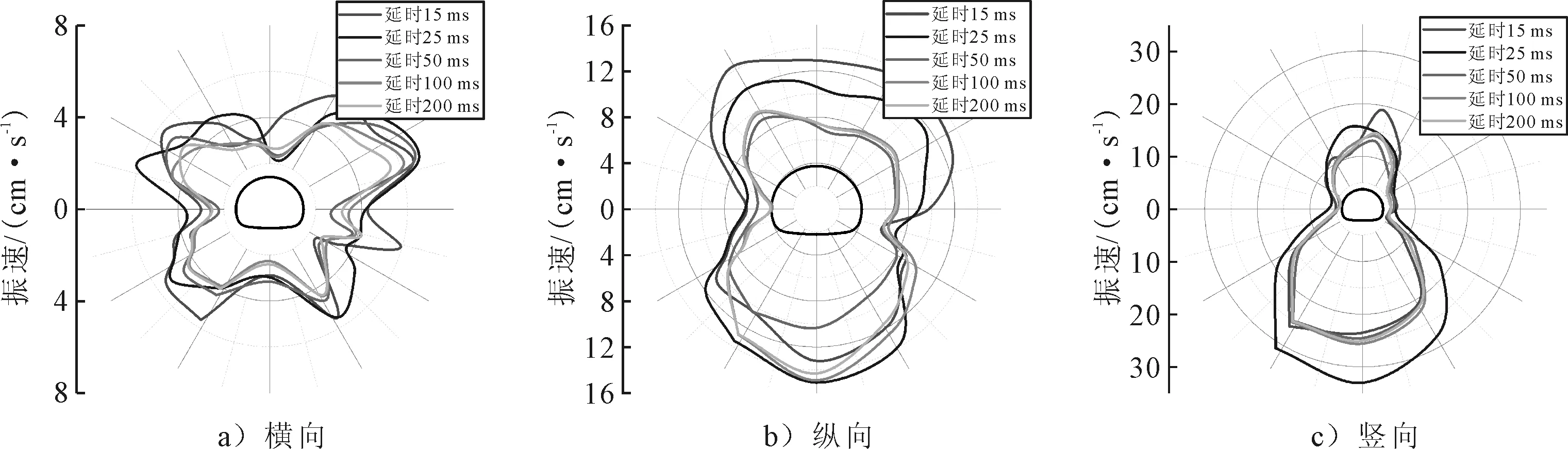
图7 R=10.0 m截面峰值振速分布图

图8 R=19.0 m截面峰值振速分布图

由图6～8可知，①延时15和25 ms产生的振速峰值相对较大.两种延时时间产生的振速峰值互有领先的情况，说明在0～50 ms范围内并不是延时越大对振速的降低效果越好，反而可能因为两个不同周期序列的波相互叠加而增大振幅.②延时50 ms相较15 ms和25 ms产生的振速峰值已经有较大程度的减小，有效地避免了两段荷载的互相影响.③延时100 ms以上时对降低振速产生的增益效果已经不太明显.延时100和200 ms的振速峰值曲线基本重合.过大的延时间隔已起不到更好地减振效果.④为避免两段爆炸荷载的相互影响、叠加，延时间隔在50 ms时已经具有较好地效果，同时结合毫秒雷管的段数，延时在50 ms至150 ms时即可满足常规隧道爆破的需要.

2.2 隧道爆破振动影响因素

炸药类型、最大段装药量、高程差、爆破参数等因素都会对最终产生的爆破振动效应造成相应的影响.

如果选用的微差间隔时间比较合适，便能试爆破振动大幅度地相互抵消.Langefors等[6]研究发现，在爆破振动周期T及波形保持不变时，如果选用Δt=T/2的微差时间间隔，能够最大幅度地使振动相互抵消.但是现实中的微差爆破振动的相互干扰是十分复杂的，需要对地质地貌和爆破参数等众多条件进行综合的分析考量[7].

掏槽眼爆破时仅有掌子面一个临空面，其受到的限制效果较大，因而比较多的爆破能量传导到了围岩内部，使得围岩产生的振动速度比较大.伴随着爆破临空面的增加，相同的炸药量情况下围岩产生的振动速度会逐渐减小[8].

3 不同间距爆破对邻近隧道衬砌的影响

3.1 沿隧道轴向振速分布分析

沿隧道轴向在爆破掌子面前后方每3 m选取一个截面，距离正值为掌子面前方，距离负值为掌子面后方.每个截面取四个关键点，分别为拱顶、两侧拱腰和拱底.将各关键点的横向(Vxmax)、纵向(Vymax)和竖向(Vzmax)三个方向的振动速度峰值调取出来，见图9(D为隧道净宽).左右拱腰和拱底沿隧道轴向振速分布同理可得，限于篇幅，此处略.

图9 拱顶沿隧道轴向振速分布图

由图9可知，①拱顶、两侧拱腰和拱底在不同间距的条件下三向振速分布规律基本相同，数值有所差异.②拱顶、两侧拱腰和拱底的横向和竖向振速基本与后行隧道爆破掌子面平行的截面对称分布，间距0.5D时最大，间距1.0D次之，间距2.0D最小.③拱顶、两侧拱腰和拱底的纵向振速在与后行隧道爆破掌子面平行的截面处均出现一个波谷，然后沿隧道轴向前后方先增大后减小.④先行隧道中与后行隧道爆破掌子面平行截面前方衬砌的振速相较后方相同距离处的振速较大，这是因为后行隧道的开挖，使得两隧道间中夹岩更易受到扰动而产生振动.

3.2 截面峰值振速分布规律分析

取爆心距R=0.0 m(即与后行隧道爆破掌子面平行的截面)处和R=+6.0 m(即距与后行隧道爆破掌子面平行截面前方6.0 m)处的截面峰值振速，作隧道截面上横向(x方向)、纵向(y方向)、竖向(z方向)的峰值振速分布图，见图10～11(图中均使用极坐标系，坐标原点为隧道轮廓的中心).

图10 R=0.0 m截面峰值振速分布图

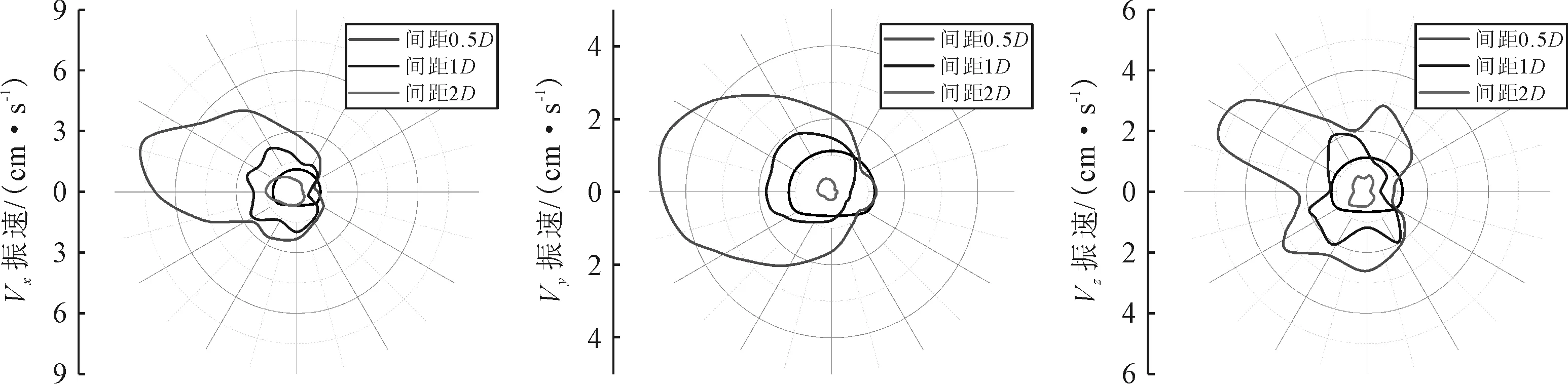
图11 R=+6.0 m截面峰值振速分布图

由图10～11可知，①在三向振速中，横向振速相较其他两个方向的振速数值上较大，如间距0.5D时R=0.0 m截面处横向振速最大值为28.08 cm/s，纵向和竖向的最大值为3.09和8.11 cm/s.②在间距0.5D时，能明显看出左侧拱腰位置三向振速相较其他位置都较大，右侧拱腰处振速较小.在R=+6.0 m截面处左拱腰处纵向振速为4.80 cm/s，右拱腰纵向振速为1.14 cm/s.整体振速分布都呈现出左侧拱腰较大的特点.③在间距1.0D时，仍能发现左侧拱腰振速较大，但在纵向振速和竖向振速中与其他部位的差距已经很小，拱顶和拱底位置已经反超左拱腰位置的振速，其规律与单洞爆破时类似.④在间距2.0D时，整体三向振速已经较低，说明后行隧道的爆破地震波在经过较长厚度的围岩传播衰减后，对先行隧道的衬砌造成的影响已经较小.

4 结 论

1) 在改变两段荷载间隔时间分别为15，25，50，100 和200 ms的条件下，分析对比了围岩的振动速度特征的变化.综合对比三向振速特征，延时15和25 ms产生的振速峰值较大，延时50 ms相较15和25 ms产生的振速峰值已经有较大程度的改善，有效地避免了两段荷载的互相影响，延时100和200 ms的振速峰值基本重合.延时在50 ～150 ms时即可以满足常规隧道减振爆破的需要.

2) 先后行隧道在间距0.5，1.0和2.0D的情况下，后行隧道爆破时，先行隧道衬砌横向振速相较其他两个方向的振速数值上较大，整体振速分布都呈现出左侧拱腰较大的特点.

3) 在间距2.0D时，整体振速已经较低，对先行隧道的衬砌造成的影响已经较小.应尽量满足先后行隧道间距2.0D，并应对迎爆侧拱腰加强监测，适时调整爆破参数.

[1] LU W, YANG J, YAN P, et al. Dynamic response of rock mass induced by the transient release of in-situ stress[J]. International Journal of Rock Mechanics & Mining Sciences,2012,53(9):129-141.

[2] LU W, YANG J, CHEN M, et al. An equivalent method for blasting vibration simulation[J]. Simulation Modelling Practice & Theory,2011,19(9):2050-2062.

[3] 王明洋,邓宏见,钱七虎.岩石中侵彻与爆炸作用的近区问题研究[J].岩石力学与工程学报,2005,24(16):2859-2863.

[4] 陈士海,王明洋,赵跃堂,等.岩石爆破破坏界面上的应力时程研究[J].岩石力学与工程学报,2003,22(11): 1784-1788.

[5] 刘京.小净距隧道爆破振动影响分析及工程应用研究[D].西安:西安建筑科技大学,2014.

[6] LANGEFORS U, KIHLSTRÖM B. The modern technique of rock blasting[M].Stockholm: Almquist and Wiksell,1963.

[7] 郭学彬,张继春,刘泉,等.微差爆破的波形叠加作用分析[J].爆破,2006,23(2):4-8.

[8] 张秀良.临空面理论在兰渝铁路LYS-2标隧道中的应用[J].兰州交通大学学报,2014(1):55-58.