基于蠕变模型的沥青混合料车辙有限元分析*

Barugahare Javilla 方 昊 磨炼同

(武汉理工大学硅酸盐建筑材料国家重点实验室 武汉 430070)

0 引 言

车辙预测作为沥青混合料设计的一个重要组成部分，已经有许多工具被用于预测车辙，包括多层弹性理论、NCHRP 1-37车辙模型和有限元分析(FEM)[1-2].在众多方法中，有限元被认为是功能最多的分析方法，在不进行实际试验测试的情况下，能够评价沥青路面内部应力和应变发展、路面结构、材料的线性及非线性行为、多轴荷载以及轮胎接触应力分布不均等对车辙发展的影响.FEM的准确性主要依赖于所用的材料本构模型，本文利用了Abaqus有限元模拟软件中的应变硬化蠕变模型来预测沥青混合料的车辙发展，该模型通常应用于偏应力加载状态或短时加载情况下.与时间硬化蠕变模型相比，该模型更准确，尤其是获得数值解；而与弹性和粘弹性材料本构模型相比，该模型也能更好的预测材料性能.该应变硬化模型为

(1)

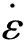
在Abaqus软件中，应变硬化蠕变模型由材料参数A，n，m，弹性模量(E)和泊松比(ν)表示.前期有限元分析研究表明，弹性材料参数E和ν只影响材料的弹性恢复，这与前人研究中的观察结果一致，因此，只有A，n和m被认为是影响沥青混合料车辙发展的参数.研究表明，当参数n保持不变时，车辙性能对参数A和m都敏感，但参数A最为显着.此外，当m保持不变时，车辙性能对A和n都敏感，但A仍然是最重要的参数.在其他关于高模量沥青混合料的相关研究中，没有参数值保持不变，随着车辙增加参数A降低、参数n增加，但参数m变化不明显.另有研究表明，参数n与接触压力相关，参数A和参数m分别为双对数坐标图中车辙和时间曲线与y轴截距值和斜率相关，参数A和n的值应该是正的，而m的值应该是负的，并且在0和-1之间.

蠕变模型参数可以从不同的测试方法确定.Uzarowski[3]基于50 ℃下三轴重复载荷蠕变试验，表明沥青混合料的参数A值的范围为1.4×10-7～1.13×10-6,n值为1.0～ 1.5,m为-0.7～-0.6.使用FEA进行的车辙模拟与实际车辙相比偏低，参数A需要增加一个2.6～4.6的校正因子来提高拟合精度.Fang等[4]基于在25 ℃温度及69～800 kPa的应力范围下对细骨料沥青混合物进行的单轴重复蠕变恢复试验和多应力加载试验的研究，提出参数A值的范围为4.7×10-6～1.03×10-5，n为0.82～0.85，m为-0.78～-0.75.

Arabani等[5]研究表明，在40℃温度和0.1和0.2 MPa应力水平下对玻璃沥青和传统沥青混合料进行单轴重复载荷试验，得到的蠕变参数A值分别为8.5×10-6和3.13×10-5；n分别为1.55和1.72，m值分别为-0.75和-0.619；当参数A的校正因子为1.3时可以准确拟合车辙试验和FEA模拟结果.Imaninasab等[6]在相同的测试方法下，对含有不用掺量橡胶的多孔沥青混合料进行了试验，得到了类似的蠕变模型参数；值得注意的是，只有n随橡胶掺量的变化而变化，参数A和n与橡胶掺量无关.

Wang等[7-8]对AC-20高模量沥青混合料在15～60 ℃的温度和应力水平0.1～0.5 MPa的条件下进行了单轴压缩蠕变试验，得到的蠕变模型参数A值范围为1.26×10-6～1.41×10-13，n为0.378～0.97，m值从-0.720～-0.914；在没有高模量添加剂的情况下，A增加到2.98×10-15～5.39×10-22，n值也增加到1.808～3.980，而m变化不大.Ebrahimi[9]在50 ℃和320 kPa应力条件下对典型的新西兰沥青混合料进行了单轴蠕变试验得到的蠕变模型参数A值范围为1.99×10-3～8.04×10-4，n值为0.319～0.347，m值为-0.697～-0.845. Sivasubramaniam等[10]对APT混合料在35～50 ℃温度和40 kN的双轮荷载下进行了试验，研究表明A值范围为1.6×10-4～3.5×10-4，m值为-0.84～-0.86，而n值保持恒定在0.8，对相同的混合料进行了的PURWheel车辙试验得到了类似的蠕变参数值范围.Mwanza[11]使用加速加载测试在35 ℃温度和轮胎接触压力为560～800 kPa条件下进行了车辙测试，将蠕变参数m值设置在常数-0.5的情况下，得到的参数A值范围为1×10-9～8×10-9，n为0.5～0.9，为了提高FEA车辙预测的准确性，参数A的校正因子为1.4.

综上所述，蠕变模型参数值并不完全依赖于材料，而是受到测试方法的显著影响.此外，在回归分析中，假定为常数的参数会对其他参数产生强烈影响，需进行深入研究以分析测试方法对参数的影响，同时更好的拟合确定的蠕变模型参数值.目前，蠕变模型参数值多采用多元回归拟合求解.根据文献[12]中的车辙测试方法，通过拟合确定了AC-13，AC-20和AC-25三种沥青混合料的蠕变模型参数值.上述三种沥青混合料广泛应用于国内高速公路沥青面层的铺筑，其结果具有一定的代表性，此外车辙试验方法应用广泛，可很好模拟实际路面的应力状态，能较好地评价混合料车辙性能[13-15].

本文通过开展室内不同温度和轮压下车辙试验拟合分析确定AC-13，AC-20和AC-25三种沥青混合料的蠕变模型参数值，再将确定的蠕变模型参数值输入以应变硬化蠕变模型为基础的有限元分析方法模拟多重应力条件下车辙发展，并与实际试验结果相比较，开展沥青面层三层组合结构的加速加载试验验证蠕变模型的可靠性.

1 原材料和试验方法

采用AC-13, AC-20, AC-25三种常见的沥青混合料级配，其中AC-13使用的是玄武岩集料，AC-20和AC-25为石灰岩集料.其中石灰岩集料的基本指标如下：表观密度2.703 g/cm3，洛杉矶磨耗22.1%，压碎值21.5%，棱角性17%；玄武岩集料的基本指标如下：表观密度2.961 g/cm3，洛杉矶磨耗7.8%，压碎值12%，棱角性12.5%.级配AC-13和AC-20所用沥青为SBS改性沥青，AC-25级配所用沥青为基质90#；SBS和90#沥青的基本指标分别为：针入度(25 ℃)72.6和84 0.1 mm，延度50 cm(SBS，5 ℃)和>100 cm(90#，15 ℃)，软化点76 ℃和46.5 ℃，通过马歇尔设计方法确定了AC-13, AC-20和AC-25三种级配的最佳油石比分别为：4.7%，4.3%和3.9%.

蠕变模型中有三个参数，理论上在同一材料和试验温度至少需要三个试验方能拟合求解，因此试验设计应结合沥青路面各层温度分布和交通受力特点，开展沥青路面上、中和下面层不同温度和不同轮压下的车辙试验，因此本文设计了三种沥青混合料在温度30～70 ℃、应力0.5～0.9 MPa之间进行了一系列单应力室内车辙试验.其中选用的轮压应力0.5, 0.7和0.9 MPa分别表示路面轻、中和重载情况，而温度范围则依据中国部分地区夏天沥青路面的典型温度进行选择.车辙试样根据文献[12]的规定，尺寸为300 mm×300 mm×50 mm；每个条件下都进行了至少三次重复试验.

为了验证模型可靠性，对AC-20混合料进行了多重应力车辙试验，三种加载顺序分别为0.5，0.7，0.9 MPa、0.7，0.9，0.5 MPa和0.9，0.7，0.5 MPa，试验温度选在30，40和50 ℃，其与高温季节时沥青路面中面层的实际温度接近.多重应力车辙试验总共加载2万次，其中第一个应力荷载施加次数为1万次，而后面二个荷载施加次数都为5 000次.通过多重应力加载模式能够研究不同轻载、正常荷载和超载组合对沥青混合料车辙发展的影响，并检验单应力车辙试验条件下确定的蠕变模型参数是否可用于解释复杂条件下沥青混合料车辙的发展.此外开展了沥青路面三层足尺加速加载试验，试件尺寸为1 000 mm×500 mm×180 mm，其中上面层AC-13厚40 mm，中面层AC-20厚60 mm，下面层AC-25厚80 mm，试验温度选在30，40和50 ℃，荷载施加次数为10万次，以验证模型对实际沥青路面结构车辙发展的预测能力.

为了比较车辙试验，采用ABAQUS有限元软件对车辙试验和沥青面层三层足尺加速加载试验进行了模拟.为了简化计算，采用二维平面应变模型，其中车辙模型长300 mm，高50 mm；沥青路面三层足尺加速加载试验模型长1 000 mm，高180 mm.模拟底部为全约束，侧面则只约束水平位移，轮压按轮宽50 mm以压力形式作用于模型表面中间位置.文献[9]在相同加载时间下对比了动荷载和静荷载区别，发现最终的沥青混合料永久应变非常接近.轮压单次作用时间等于橡胶轮接触试件长度除以橡胶轮行走速度，经过验算和实测单次碾压时应力加载时间为0.135 s，因此，为了减小模型计算时间，本文选用了二维平面模型和静荷载来分析沥青混合料车辙发展，例如，车辙试验动态加载可用静态加载进行简化模拟，动态碾压60 min对应的等效静态加载时间计算如下：60 min×42 次/min×0.135 s/次=340 s.

2 结果与分析

2.1 蠕变模型参数的获取

表1为AC-13、AC-20和AC-25沥青混合料的蠕变模型参数值，通过对10 000次循环后单应力车辙试验结果进行多变量线性回归分析得到.需指出的是蠕变应变由车辙试验深度除以试件厚度进行简化计算得到的平均值，实际上试件在轮压正下方受到的蠕变应变随厚度变化较大.由表1可知，只有参数A随着温度的升高呈现出增长的趋势，n和m对温度的依赖性并不明显.在低于50 ℃的温度下，AC-13、AC-20和AC-25三种混合料的蠕变模型参数A，n和m值的范围分别为1.4×10-3～3.7×10-3，0.5～1.3和-0.8～-0.6.当温度超过50 ℃后，只有A值受到了较大影响，范围增加到了5×10-3～7.5×10-3之间.

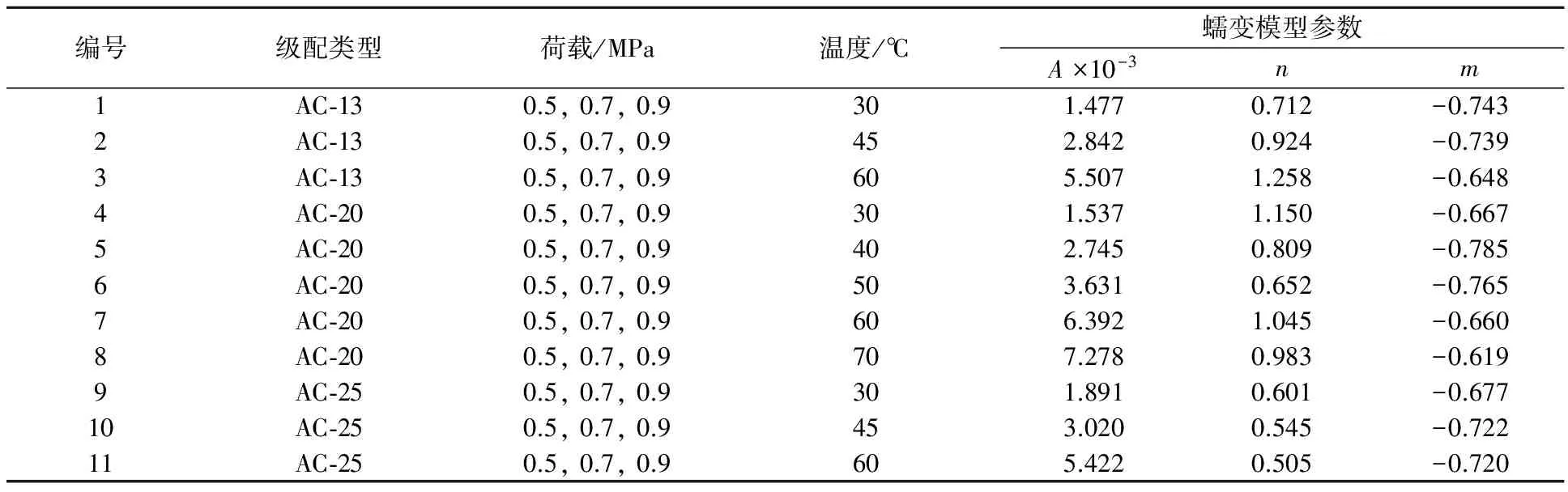
表1 不同温度和单应力水平车辙试验蠕变模型参数汇总

2.2 单应力车辙试验的有限元模拟研究

图1为在0.7 MPa和50 ℃下AC-20沥青混合料的车辙试件典型的竖向受力和变形图.由图1可知，车辙变形主要发生在轮压正下方，其中网格的变形主要发生在模型的顶部和中间部分.在模型的中间部分存在较大的推力，可能是由于轮载和模具的底部的垂直反作用力.此外，网格元素的最小变形发生在模型的底部.前面拟合采用了蠕变应变由车辙试验深度除以试件厚度进行简化计算得到的平均值，由此确定的A，n和m输入有限元FEA得到的结果会偏低，因此应进行修正.

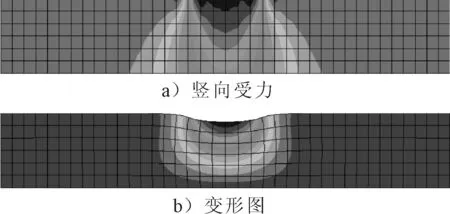
图1 0.7 MPa和50 ℃条件下AC-20混合料的FEM模拟图

图2为不同温度和轮压下AC-13、AC-20和AC-25混合料的单应力车辙试验结果和FEA模拟结果的对比.三层所选取代表性温度主要反映夏季高温条件下典型三层沥青面层结构的温度分布.FEA模拟时采用了表1所列蠕变模型参数值，其因拟合求解时采用了平均简化蠕变应变而与实际试件内部受到的蠕变应变存在差异，为了更准确的拟合FEM模拟结果和实际测试结果，对蠕变模型参数A进行了校正，表2为不同级配不同温度下A的校正因子，其范围为1.2～1.5，校正后所有数据拟合的相关系数R2均大于98.5%.从表2中可以看到AC-13和AC-20沥青混合料车辙试验温度低于50℃时，A的校正因子在1.2～1.3，而在当当试验温度高于60℃时达到了1.4～1.5；相对而言， AC-25沥青混合料的A的校正因子对温度不敏感，一直保持在1.2.采用了表2的校正因子后，FEM模拟曲线基本与车辙试验结果具有很高的重合度，可很好的预测车辙的发展.

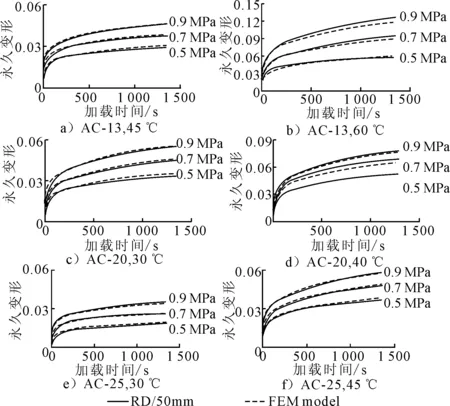
图2 不同温度和单应力作用下车辙试验和FEM模拟结果对比

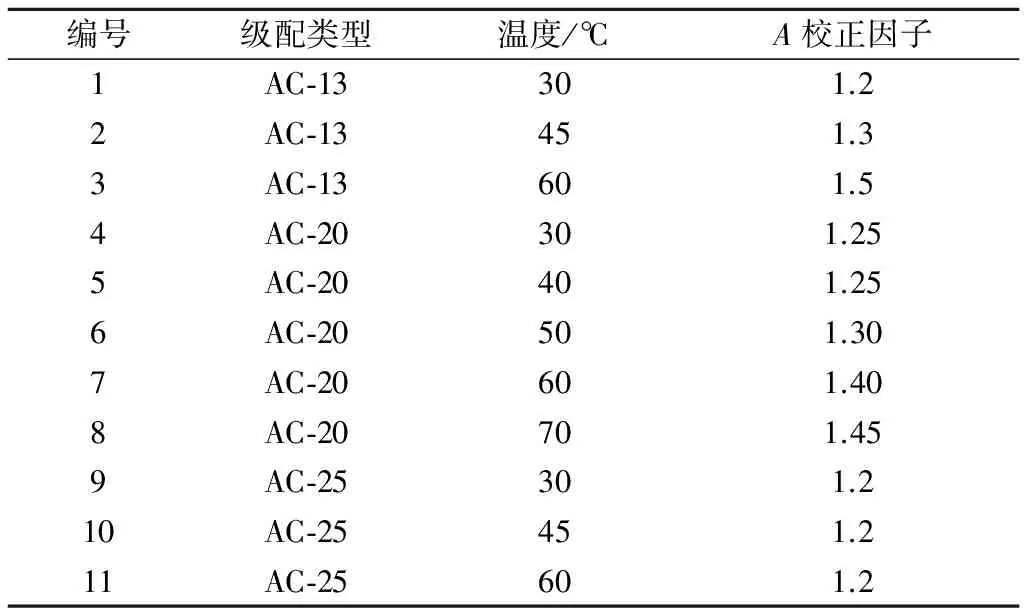
编号级配类型温度/℃A校正因子1AC⁃13301．22AC⁃13451．33AC⁃13601．54AC⁃20301．255AC⁃20401．256AC⁃20501．307AC⁃20601．408AC⁃20701．459AC⁃25301．210AC⁃25451．211AC⁃25601．2

2.3 多应力室内车辙试验的有限元分析研究

图3为AC-20混合料的多应力车辙试验结果和基于应变蠕变模型的FEA模拟结果的对比.FEM模拟所使用的蠕变模型参数来源于表1中单应力车辙试验结果.表3为蠕变模型参数A的校正因子，其范围在1.05～1.2，与表2中的范围相同；应用校正后的参数，可以得到更准确FEM模拟结果(R2大于98.5%).根据实际测试和FEM模拟结果，可以看到，首先施加重载导致了最大的车辙损伤，并且在重载之后施加较轻荷载车辙破坏将变得不明显.此外，车辙变形速率随着荷载的增加而增加.一般的，单应力车辙试验不足以准确模拟实际路面多重应力荷载下的车辙，由图3可知，通过这种简单试验确定的蠕变参数可用于基于应变硬化蠕变模型的FEA分析研究，并且能够准确模拟多重荷载条件的影响.

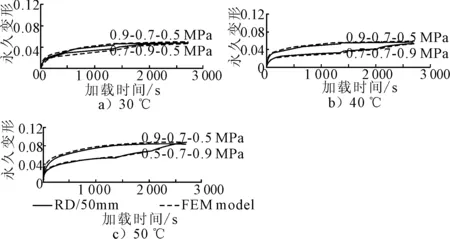
图3 同条件下多应力车辙试验结果和FEM模拟结果对比

编号级配类型温度/℃A校正因子1AC⁃20301．092AC⁃20401．053AC⁃20501．2

2.4 沥青面层三层足尺加速加载试验和验证

图4为0.7 MPa和40 ℃条件下沥青面层三层结构层足尺加速加载试验的有限元FEM模拟竖向受力和变形状况.由图4可知，沥青面层三层结构层由上面层AC-13受力最大，中面层次之，而下面层AC-25受力最小，因此，整个沥青结构层的蠕变变形由上述三层叠加而成，其中主要上面层贡献最大.

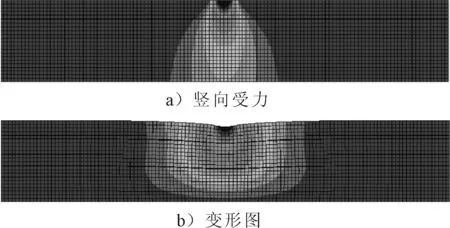
图4 0.7 MPa和50 ℃条件下沥青三层结构层足尺加速加载试验的FEM模拟图

图5为沥青三层结构层足尺加速加载试验与FEM模拟对比分析图，由图5可知，蠕变模型在试验温度为30 ℃和40 ℃时具有很好的一致性.当温度增高到50 ℃时，模拟结果略低于试验值.整体而言，有限元模拟很好的反映了温度对沥青面层车辙的影响，可用于实际路面车辙的预测.

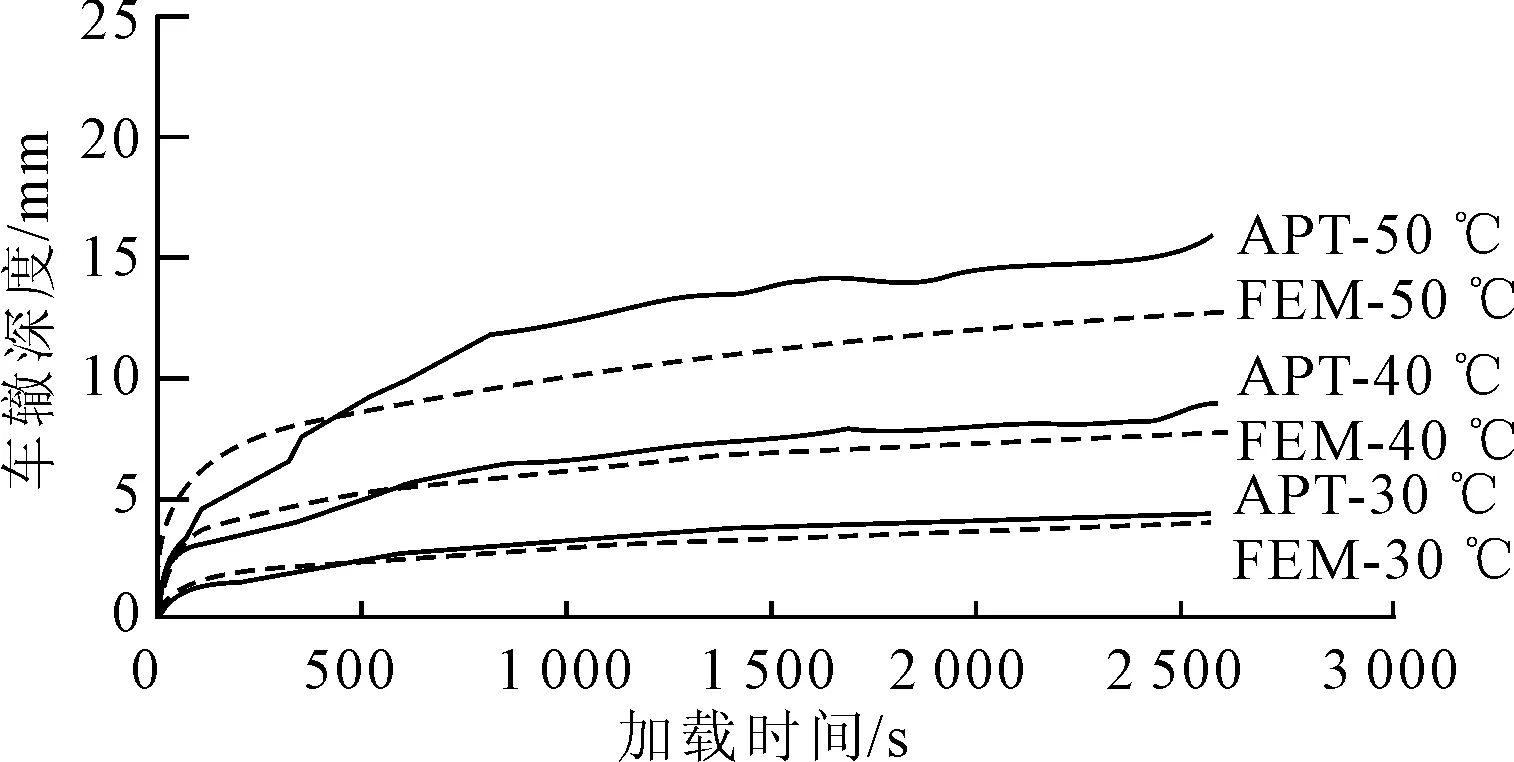
图5 沥青三层结构层足尺加速加载试验与FEM模拟对比分析

3 结 束 语

本文利用基于应变硬化蠕变模型的有限元分析对AC-13、AC-20和AC-25三种沥青混合料在单应力和多重应力加载下的车辙发展进行了模拟分析，并开展了沥青三层结构层足尺加速加载试验进行模型验证.试验和模拟结果证实AC-13，AC-20，AC-25沥青混合料的蠕变模型参数(A，n和m)可以基于简单的单应力车辙试验来确定，其中A，n和m的取值范围分别为1.4×10-3～7.5×10-3，0.5～1.3和-0.6～-0.8.在实际模拟路面车辙时，系数A应施加一个范围为1.2～1.5的校正因子，以提高模拟的可靠度.整体而言，基于应变硬化蠕变模型的有限元分析可较好的模拟沥青混合料在多重荷载下的车辙性能，可用于复杂交通条件下沥青路面车辙的预测.

[1] 朱乔.基于ANSYS 有限元分析的沥青路面车辙研究[D].武汉：湖北工业大学,2015.

[2] 王甲勇.基于车辙试验的有限元车辙预估及影响因素分析[D].西安:长安大学,2009.

[3] UZAROWSKI L. The development of asphalt mix creep parameters and finite element modeling of asphalt rutting[D].Waterloo: University of Waterloo,2007.

[4] FANG H B, HADDOCK J E, WHITE T D, et al. On the characterization of flexible pavement rutting using creep model-based finite element analysis[J]. Finite Elements in Analysis and Design,2004,41(1):49-73.

[5] ARABANI M, JAMSHIDI R, SADEGHNEJAD M. Using of 2D finite element modeling to predict the glasphalt mixture rutting behavior[J]. Construction and Building Materials, 2014,68:183-191.

[6] IMANINASAB R, BAKHSHI B, SHIRINI B. Rutting performance of rubberized porous asphalt using Finite Element Method (FEM)[J]. Construction and Building Materials, 2016,106:382-391.

[7] WANG X, FAN T, KITMENG L. Finite element analysis on the creep constitutive equation of high modulus asphalt concrete[J]. Advances in Materials Science and Engineering, 2015(1):58-62.

[8] ZHENG M, HAN L, QIU Z, et al. Simulation of permanent deformation in high-modulus asphalt pavement using the Bailey-Norton creep law[J]. Journal of Materials in Civil Engineering,2016,28(7):578-582.

[9] EBRAHIMI M. Modelling for New Zealand hot mix asphalts[D]. Christchurch :University of Canterbury, 2015.

[10] SIVASUBRAMANIAM S, HADDOCK J E. Validation of superpave mixture design and analysis procedures using the NCAT test track[J]. Joint Transportation Research Program, 2006(2):252-258.

[11] MWANZA A D. Modeling of rutting prediction for flexible pavements in Zambia[D]. Xi’an :Chang’an University, 2013.

[12] 交通部公路科学研究所.公路工程沥青及沥青混合料试验规程：JTG E20—2011 [S].北京：人民交通出版社,2011.

[13] HU X, FARUK A N M, ZHANG J, et al. Effects of tire inclination (turning traffic) and dynamic loading on the pavement stress-strain responses using 3-D finite element modeling[J]. International Journal of Pavement Research and Technology, 2017(1):55-58.

[14] JAVILLA B, MO L, HAO F, et al. Systematic comparison of two-stage analytical rutting models of asphalt mixtures[J]. Construction and Building Materials, 2017,153:716-727.

[15] JAVILLA B, MO L, HAO F, et al. Multi-stress loading effect on rutting performance of asphalt mixtures based on wheel tracking testing[J]. Construction and Building Materials, 2017,148:1-9.