汽车空气弹簧特性分析

陈平亮 ， 李殿起 ， 刘光辉， 魏爽

（沈阳工业大学机械工程学院，沈阳 110870）

0 引言

拥有空气弹簧的车辆在曲折路面行驶时由于空气弹簧具有刚度特性、振动频率，可以使车具有较好的行驶平顺性和行驶稳定性，并可有效地保证了轮胎与路面的优良附着力，还可以有效地减少车辆对路面的破坏能力，进而提高车辆在高速行驶时的操纵稳定性和行驶安全性[1]。如图1是金龙某款客车的空气弹簧的实物装配图，对空气弹簧动力学特性的研究可以更好地完善空气悬架的动力学体系，并用CATIA绘制的空气弹簧模型来进一步完善研究内容,如图2所示。膜式空气弹簧在底部设计有橡胶气囊，可以通过改变气囊挠曲变形来完成空气弹簧的伸缩变化，这种设计的弹性效果比囊式空气弹簧更为合理，膜式空气弹簧在良好工况下运动时，还可以通过改变底座形状大小的方式来控制空气弹簧有效面积的变化率，由于独特的设计理念膜式空气弹簧的自振频率一般在最合适范围内变化，以此可得到相对理想的特性效果。

1 垂向刚度特性

空气弹簧主要承受垂向载荷和横向载荷,由于横向载荷对汽车影响较小,故主要分析垂向载荷对汽车行驶性能的影响，汽车的垂向载荷的变化特点可以用刚度特性来展现，因此创建空气弹簧的简化力学模型[2-3]，如图3所示。

图3中所示参数含义:F表示空气弹簧的垂直方向的载荷；K1表示刚度与有效面积容积的压力变化率；K2表示有效面积变化率；K3表示附加气室容积变化率；C表示空气弹簧阻尼变化率。

图1 金龙客车某款客车空气弹簧

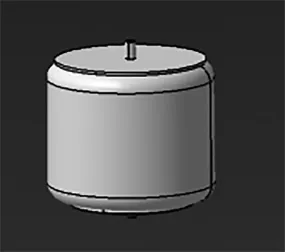
图2 空气弹簧模型

图3 空气弹簧力学模型

空气弹簧力学平衡方程式:

式中：P1为内部气体的绝对压强；Pa为橡胶容积外部的大气压；Sa为作用力所承载的有效面积。

经过试验验证得，汽车在外力力作用下空气弹簧上接触面的有效承载面积是不断发生变化的。空气弹簧在正常工况下运行时，空气弹簧的高度会随着载荷的变化而发生一定的变化，变化过程主要是改变气囊的容积来实现的，气囊容积是由气压来决定的。

假设空气弹簧内所用的气体处于理想状态下，那么得到气体状态方程为

式中：P为设计状态的气体绝对压强；V0为设计正常高度时的气体容积；m为多变指数，等温过程m=1.0；绝热过程m=1.4；一般状态过程m=1.3～1.38[4]。

将式（2）代入式（1）得到

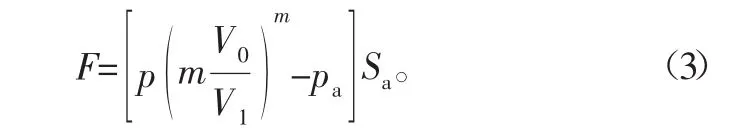
对式（3）进行纵向位移Z的求导计算，可运算得到气囊的垂向刚度[5]表达式为

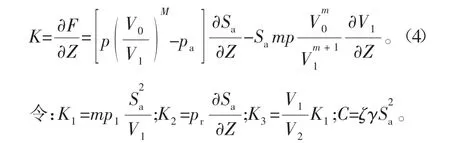
式中：ζ为气体流动中产生的阻尼系数；γ为初始设计时的囊内气体比重。

假设汽车在正常行驶过程中对空气弹簧影响较小时，由于气囊变化较小故可以忽略腔内体积的变化[6]，此时可以进一步假设阻尼变化为0，那么式子（4）可以进一步化简为

运动过程中空气弹簧有效承载面积的变化较小，可以忽略其他因素的影响，公式（5）还可以化简为

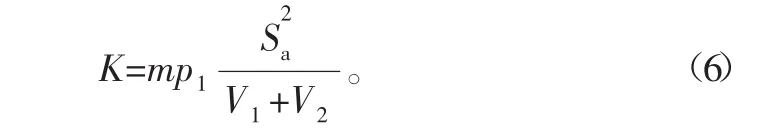
由公式（6）可知，当m、p1、Sa一定时，K与V1+V2的关系是成反比例函数变化，变化形式如图4所示,V1+V2的变化越大，其K值的变化越小，故在设计时一般按照腔内容积比变化较大而刚度比变化较小来设计[7]。

图4 刚度K和容积V1+V2的关系

如果在汽车运动过程中，由于振动较小，故气囊变形也较小，在较小变形下腔内容积的变化可以忽略不计，而设此时的阻尼值为无穷大，则增加的附加气室就不会影响空气弹簧的垂向刚度，可将式（4）化简为

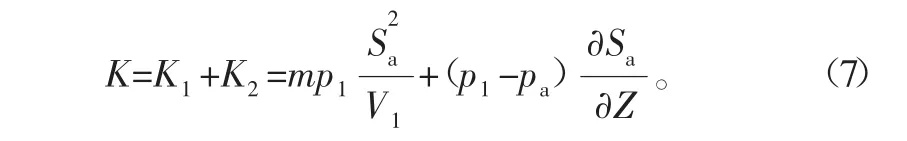
由式（5）和式（7）式可知，空气弹簧的K值变化既与初始设计高度下的内部气体压强和容积有关[8]，还与运动过程中上接触面所受作用力而产生的有效面积变化率有关。对于空气弹簧的气囊外形设计完成的情况下，还可以通过改变底座垫片的外形来获得在不同初始容积下的工作环境，通过对垫片的改变可以使汽车悬架承受不同的有效承载面积。另外还可以通过改变垫片的形状特征（常见形状有圆柱和圆锥等）来得到所需的刚度特性。

2 空气弹簧的频率特性

2.1 固有频率

根据公式f=（1/2π）（k/m）-2可得其固有频率的计算表达式为

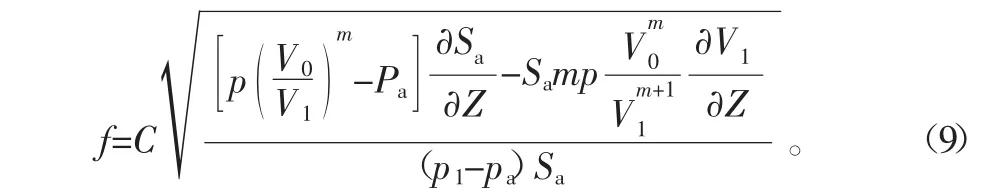
若设dv/ds=-Ae，式（9）可看出，空气弹簧f值与其有效面积变化率dAe/ds有关，dAe/ds变大，则f值也随之变大[9]，假设通过改变dAe/ds来降低f值，将dAe/ds的比值设计成负值即可。由于式（9）计算过程比较复杂，实际计算中可以进行适当简化，通过实验验证后可得到简化后的固有频率f与压力P之间的关系（在假设对约束膜式空气弹簧时可令Ae=cons t），简化后计算公式为

式中：P为此时此刻气囊内部的绝对气压值。

对式（8）、式（9）、式（10）的计算结果进行综合分析比较可得，空气弹簧系统的f值与气囊内部气体压力成正相关，由于空气弹簧内部气体压力时刻改变，故f值也会时刻在变化，但变化幅度不大，设计时满足可控范围即可。

2.2 自振频率

由于有些空气弹簧上表面在设计时上表面使用钢板固定，上表面的有效面积几乎保持不变，即可得承载能力和其簧上质量成一次函数变化关系，并假设不存在预应力和动力传递[10]，可得其自振频率f0为

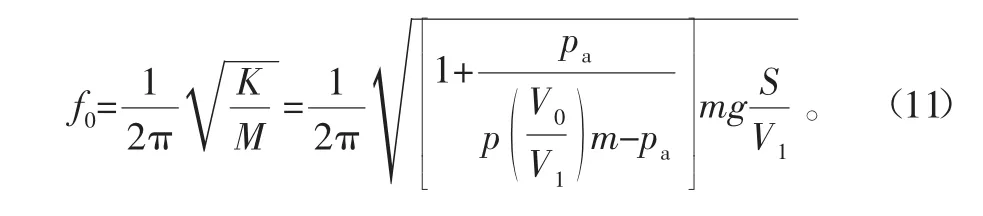
若气囊内部容积计算公式为V1=hs，可将式（11）进一步简化为

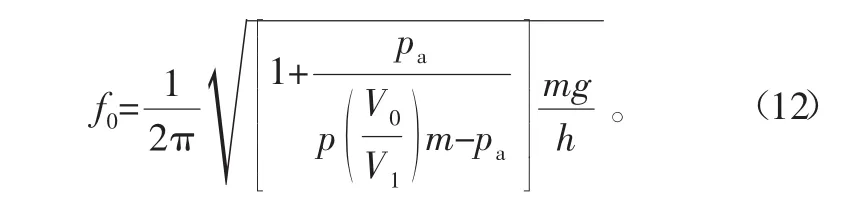
式中，h为设计时的内部气囊高度。

由式（12）可知，f0的变化只和V0/V1的变化值和空气弹簧设计时的内部气囊高度h有关，与簧载质量变化无关。

3 结 语

本文主要对空气弹簧的刚度特性和频率特性进行研究，研究得空气弹簧的K值变化不仅与初始状态的压力和容积有关，还与dAe/ds的变化和体积变化率有关。f值和f0值的变化主要受气囊高度h的影响大，在设计时应选择合适高度来匹配频率的变化。

[1] WOODROOFFE J.Heavy Truck Suspension Dynamics:Methods for Evaluating Suspension Road Friendliness and Ride Quality[C]//SAE International Truck and Bus Meeting and Exposition.1996.

[2] 张士义,张先彤,陈时锦.空气弹簧隔振技术[J].航空精密制造技术,1995(2):6-8.

[3] 李芾,付茂海,黄运华.空气弹簧动力学特性参数分析[J].西南交通大学学报,2003,38(3):276-281.

[4] 何锋,徐军,杨洪江.商用车空气悬架的关键技术分析[J].农机化研究,2005(2):236-240.

[5] 王家胜.带附加空气室空气弹簧动力学特性研究[D].南京:南京农业大学,2009.

[6] 张宝红.空气弹簧特性分析及参数化设计[D].石家庄:石家庄铁道大学,2013.

[7] 陈龙,赵华伟,江浩斌,等.空气弹簧刚度特性模型及气体非理想化修正方法研究[J].汽车技术,2010(4):29-33.

[8] CROCE P,ORSINI P,SALVATORE W.Vibration isolation and design of automotive test benches[J].Engineering Structures,2001,23(8):945-956.

[9] TOYOFUKU K,YAMADA C,KAGAWA T,et al.Study on dynamic characteristic analysis of air spring with auxiliary chamber[J].Jsae Review,1999,20(3):349-355.

[10]BOUAZARA M,RICHARD M J,BOUAZARA M,et al.An optimization method designed to improve 3-D vehicle comfort and road holding capability through the use of active and semiactive suspensions[J].European Journal of Mechanics,2001,20(3):509-520.