ARIMA模型在医院流产数时间趋势分析中的应用*

昆山市第一人民医院妇产科(215300) 毛圆圆 周丽红 刘 丽 刘 琴

人工流产率在发达国家已经出现下降趋势，但是发展中国家依旧呈现上升趋势[1]。具有医学终止妊娠(人工流产)的经历，在中国育龄妇女中是比较普遍的现象，基于人群的调查显示育龄妇女中具有人工流产史者占22.0%～50%[2-3]，其原因主要是无保护措施的性交和避孕失败[4]。合理的人工流产可减小不必要的妊娠结局，频繁的人工流产可增加后来习惯性流产风险[5]，乃至女性恶性肿瘤患病风险[6]。本研究基于医院人工流产登记来探究2013-2016年人工流产病例数，为临床决策及指导计划生育工作实践提供依据。

对象与方法

1.对象来源

医院人工流产(简称“流产”)病例来源于2013年1月至2016年12月份昆山市第一人民医院计划生育门诊登记。

2.X-12过程

X-12过程是由美国国情调查局于1965年编制的时间序列季节调整方案[7]。其基本思想是时间序列的确定性因素分解法。基于这样的假设：任何时间序列Xt都可以拆分为长期趋势Tt、季节波动St、不规则波动It的影响。经济学家也发现经济时间序列中周期波动Dt也是一个很重要的影响因素，因此任何一个时间序列可以分解为：

乘法模型：Xt=Tt×St×Dt×It

加法模型：Xt=Tt+St+Dt+It

X-12模型见文献[8-9]。SAS统计学软件中，X-12过程可自动选择最优ARIMA模型[7,10]。

3.ARIMA模型

ARIMA模型全称为差分自回归移动平均模型(autoregressive integrated moving average model,ARIMA)，其中ARIMA(p,d,q)可拆分自回归平均移动模型，AR是自回归，p是自回归阶数；MA是移动平均，q是移动平均阶数，d为时间序列成为平稳所作出的差分阶数。标准具有季节性的ARIMA模型为ARIMA(p,d,q)×(P,D,Q)S，其中p、d、q分别表示非季节性自回归阶数、差分阶数和移动平均阶数，P、D、Q分别表示季节性自回归阶数、差分阶数和移动平均阶数，S表示季节性周期。

ARIMA建模包括：①序列的平稳化处理；②模型的识别：通过差分确定d和D的阶数，再依据差分后的自相关函数(ACF)和偏自相关函数(PACF)的图形来初步确定模型中的p、q、P、Q的阶数；③模型参数估计和检验；④模型诊断检验；⑤模型拟合效果验证和预测[11]。

4.数据分析

(1)平均绝对误差(MAE)

(2)平均绝对百分比误差(MAPE)

(3)决定系数(R2)

最后用建立的模型对2017年1月至2017年12月医院流产数进行预测。

结 果

1.原始序列趋势成分分解与季节性分析

2013年1月至2016年12月流产病例数X-12过程分析显示(图1)，4年期间分月份流产病例随时间变化趋势每年大致相同，不同年份之间均存在高峰和低谷现象。季节指数图提示每年3月份和5月份是流产高峰，而9月份是低谷，10～12月份呈现回升现象。在假定稳定性的前提下确定是否存在季节性，检验结果提示在0.01水平上具有季节性(F=9.58，P<0.01)，可见医院流产数具有周期性和季节性。

从趋势拟合来看，2013年1月至2015年7月份，流产数呈现上升趋势，但是2015年8月至2016年12月份，流产数呈现明显下降趋势。见图1。

图1 2013-2016年流产数时间序列

2.序列平稳化及适应性检验

由图1中原始序列可以看出，2013年1月至2016年12月医院月度流产例数波动较大，说明该序列是具有周期性的不平稳序列，不适合建模和预测。为了使序列平稳化，对人流例数进行一阶差分来消除趋势性，12步差分来消除季节性因素，差分后的序列图见图2。

图2 医院人流数时间序列诊断图

模型的适应性检验中，检验统计量LB(6)、LB(12)、LB(18)、LB(24)对应的P值均大于0.05，拒绝了残差序列为白噪声的假设，时间序列为非白噪声平稳序列。结合差分后的序列图和模型适应性检验，可以认为现有序列符合ARIMA乘积季节模型对平稳性的要求。

3.X-12过程自动选择最优ARIMA模型

在X-12模型中，按照BIC最小原则、拟合效果及残差分析等进行综合判断，筛选出备选模型，共进行16次试验，经过初步筛选优选出5个最佳模型，分别为(0,1,1)×(1,0,1)12、(1,1,1)×(1,0,1)12、(0,1,2)×(1,0,1)12、(1,1,0)×(1,0,1)12和(0,1,1)×(1,0,0)12，其BIC值分别为564.07、564.08、565.01、565.27和566.48。以BIC值最小为原则，发现ARIMA (0,1,1)×(1,0,1)12最优模型，季节性自回归参数、非季节性移动平均参数及季节性移动平均参数均有统计学意义(P<0.0001)。见表1。

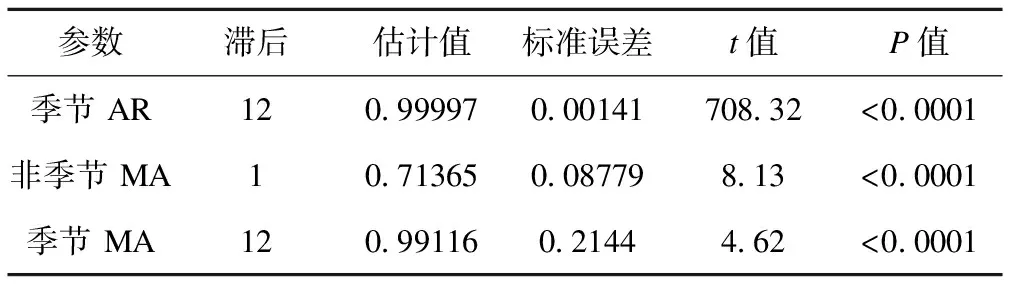
表1 ARIMA(0,1,1)×(1,0,1)12模型参数估计

4.精度评价及预测

用X-12选择的ARIMA (0,1,1)×(1,0,1)12模型中2014年2月至2016年12月实际值与预测值进行模型精度评价。结果显示月度流产数平均绝对误差为36.7例，平均绝对百分比误差为3.60%，决定系数为0.751。提示预测模型精度较高，模型较为稳健。其他候选模型精度评价见表2。

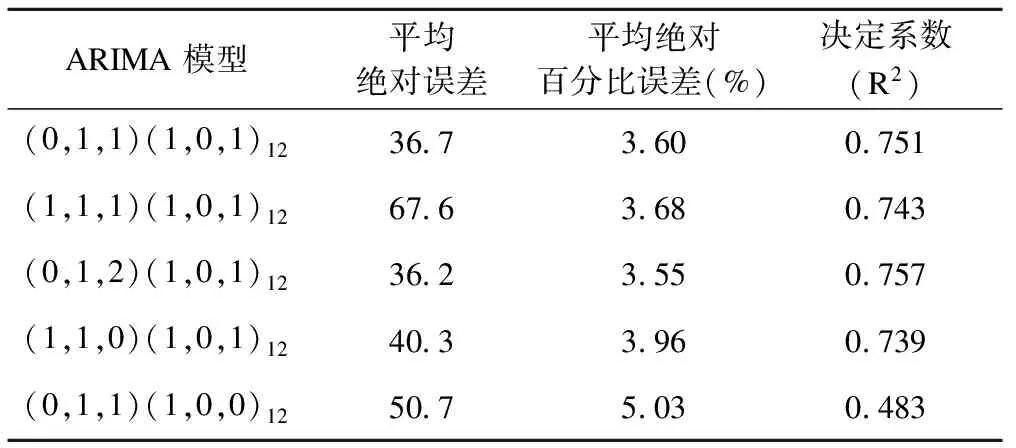
表2 X-12自动选择的5个最佳模型及其对应的精度估计值

进一步外推预测2017年1月至12月流产数。图3显示了模型对2017年1月至2017年12月流产数的预测值及其95%CI，可见模型对实际值进行了较好的拟合，预测数与实际值的动态趋势基本吻合，2017年1月至12月的预测流产数总体上保持了历史月份的波动特征。

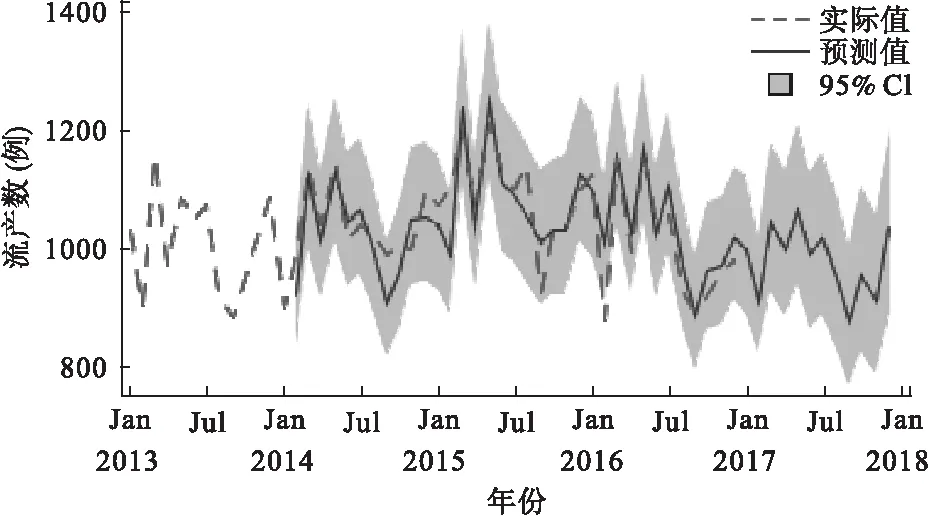
图3 X-12-ARIMA模型预测流产数时间趋势

讨 论

本研究采用X-12过程进行时间序列成分分解，以2013-2016年四年分月份流产数建模并预测2017年1至12月份流产数，结果提示ARIMA (0,1,1)×(1,0,1)12模型具有较好的拟合优度，预测精度较高，可用于流产数时间序列预测。

本研究中采用X-12-ARIMA模型，对原始数据进行了成分分解，以准确判断流产数时间序列特征。在剔除季节波动和不规则项等因素之后，流产数长期趋势曲线显得更为平滑，且明确呈现了观察时间内的变化趋势。总体上看，2013年1月至2015年7月流产数呈现平稳上升趋势，但是2015年8月至2016年12月份呈现平稳下降趋势。

本研究显示ARIMA (0,1,1)×(1,0,1)12模型对基层医院流产数建模具有较好的拟合优度，可以用于基层医院流产数预测及相关干预效果的评价。但是我们也注意到，2016年2月份具有较高的绝对误差(129例)，明显与春节相关。本次ARIMA时间序列模型构建和预测中，2016年以及2017年流产数下降的原因，一方面与国家宏观计划生育政策息息相关。党的十八届五中全会明确提出“坚持计划生育的基本国策，完善人口发展战略，全面实施一对夫妇可生育两个孩子的政策”。但是有研究显示，有关人口政策对流产的影响有限[1,12]。另一方面也与昆山市人口流动密切相关。研究显示流动人口中流产率高于其他群体[13]。昆山作为外向型经济的长三角样本，随着国家产业转移与经济结构优化升级，劳动力密集型企业逐渐淡出昆山，流动人口数量逐渐减少，可能是流产数下降的原因之一，但尚缺乏确切的权威数据。

我们采用X-12-ARIMA季节调整方法呈现了流产数时间序列特点[9,14-15]，特别是经过季节调整后，更加直观的看到基层医院分月份的流产数发展趋势。X-12-ARIMA季节调整方法也存在不足，一是经过调整的分析数据相比原始数据更难理解；目前相关的分析方法源自于美国，调整方法也根据国外的假日规则来计算，而我国的春节、国庆长假等假期因素并未进行调整。因此，该方法分析国内数据尚显不足，需要结合我国社会数据特点进行调整，更好的为相关序列分析服务。

总之，本研究采用的ARIMA (0,1,1)×(1,0,1)12模型在前瞻性预测昆山市第一人民医院流产数中具有一定的把握度，可评价已经采取的计划生育措施的效果，同时也为计划生育相关部门前瞻性决策提供依据。但是我们也看到，虽然2016年流产数呈现下降趋势，但是实施流产的例数依旧很大，进一步加强计划生育相关措施来促进这种下降趋势依旧必要。

[1] Sedgh G,Bearak J,Singh S,et al.Abortion incidence between 1990 and 2014:global,regional,and subregional levels and trends.Lancet,2016,388(10041):258-267.

[2] Gao GP,Zhang RJ,Zhang XJ,et al.Prevalence and associated factors of induced abortion among rural married women:a cross-sectional survey in Anhui,China.J Obstet Gynaecol Res,2015,41(3):383-391.

[3] 郭沛沛,刘玉玲,汤福想,等.2956例人工流产女性现状分析及人工流产后关爱服务在生殖健康中的作用评价.中国全科医学,2016,19(24):2982-2985.

[4] Wu S,Tian L,Xu F.Induced abortion and relevant factors among women seeking abortion in Nanjing,China.Gynecol Obstet Invest,2011,71(2):87-92.

[5] Sun Y,Che Y,Gao E,et al.Induced abortion and risk of subsequent miscarriage.Int J Epidemiol,2003,32(3):449-454.

[6] Huang Y,Zhang X,Li W,et al.A meta-analysis of the association between induced abortion and breast cancer risk among Chinese females.Cancer Causes Control,2014,25(2):227-236.

[7] US Bureau of the Census (2010).X-12-ARIMA Seasonal Adjustment Program,Version 0.3//US BUREAU OF THE CENSUS.Washington,DC.http://www.census.gov/srd/www/x12a/.2010.

[8] 俞艳,胡兴帮,任苏蕊,等.基于X-12-ARIMA方法的武汉市空气污染指数波动分析.环境污染与防治,2016,38(2):19-22+28.

[9] 申铜倩,刘文东,胡建利,等.x-11-ARIMA过程在痢疾疫情预测中的应用研究.中国卫生统计,2014,31(3):395-398.

[10] 孙玉环.X-12-ARIMA方法的SAS程序实现及应用.统计与决策,2006,(4):139-141.

[11] 黎健,吴寰宇,李燕婷,等.上海市痢疾发病率预测自回归求和移动平均模型的构建与应用.中华预防医学杂志,2010,44(1):48-53.

[12] Sedgh G,Singh S,Shah IH,et al.Induced abortion:incidence and trends worldwide from 1995 to 2008.Lancet,2012,379(9816):625-632.

[13] 郭超,刘鸿雁,裴晓东,等.中国五城市流动育龄妇女人工流产风险因素研究.中华流行病学杂志,2012,33(12):1238-1242.

[14] 高明,唐顺,徐福文.医院数据挖掘平台中X-11-ARIMA预测模型的应用研究.中国卫生统计,2016,33(1):139-141.

[15] 郭志武,蒲继红,滕国召.基于ARIMA模型的春节因素调整方法研究.中国卫生统计,2009,26(6):573-579.