基于超混沌的伪随机数发生器的FPGA设计
2018-03-05齐国元胡玉庆万彰凯
齐国元,胡玉庆,万彰凯
(天津工业大学 电气工程与自动化学院,天津 300387)
混沌系统是一种复杂的非线性运动,它对初始条件具有高度的敏感性,运动轨道长期不可预测,因此混沌系统表现出非常好的密码学特性[1].近年来人们致力于基于混沌的伪随机数发生器(CPRNG)的研究与设计[2-4].随着数字化技术的发展,可编程逻辑门阵列(FPGA)具有速度快、并行处理、成本低等特性,因此越来越多的借助FPGA技术设计和实现伪随机数发生器[5-8].超混沌系统一般具有多个正的Lyapunov指数,这意味着系统的运动向多个方向扩展,因此超混沌系统较一般的混沌系统具有更强的随机性和不可预测性[9-10].但目前基于超混的伪随机数发生器设计大多存在资源占用较高以及混沌迭代次数多等问题[11-13].本文根据IEEE-754浮点数标准,设计并实现32位单精度浮点数伪随机数发生器.基于Qi超混沌系统,采用Verilog硬件描述语言构建了超混沌系统模块、数据发送模块、数据缓存模块等.采用分时复用的方法仅构建一个方程计算模型,通过状态机控制四维超混沌的迭代计算,可以很好地节省硬件资源的占用.根据计算机浮点数格式的特点,选取某一取浮点数状态变量为基准,取其尾数部分一定位数与其他状态变量相异或输出,可以得到任意长度的伪随机序列,大大减少系统迭代次数,提高伪随机序列产生的效率.
1 伪随机数发生器的FPGA设计
1.1 系统整体结构
基于FPGA硬件系统设计伪随机数发生器,并要求能与计算机进行数据通信.伪随机数发生器的系统结构图如图1所示.
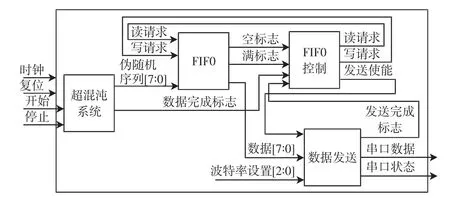
图1 系统结构图Fig.1 System structure diagram
由图1可见,该系统主要包括超混沌系统模块、先入先出存储器模块(FIFO)、FIFO控制模块及数据发送模块.超混沌系统模块是核心算法模块,主要实现混沌系统迭代计算及伪随机序列的生成.FIFO模块调用自IP核,用于数据缓存,可实现高速的超混沌系统模块数据与发送模块的数据交互.FIFO控制模块用于控制FIFO的数据读写以及发送模块的使能.数据发送模块根据一定的波特率对由超混沌系统模块生成的伪随机序列通过串口发送到计算机.
1.2 各功能模块的设计
1.2.1 超混沌系统模块
Qi等提出的超混沌系统是一个四维连续非线性系统,其2个正Lyapunov指数最大分别为13和3;并且具有较宽的频谱,其带宽是一般混沌系统甚至有些超混沌系统的20~30倍[14-15].Qi超混沌系统表达式为:
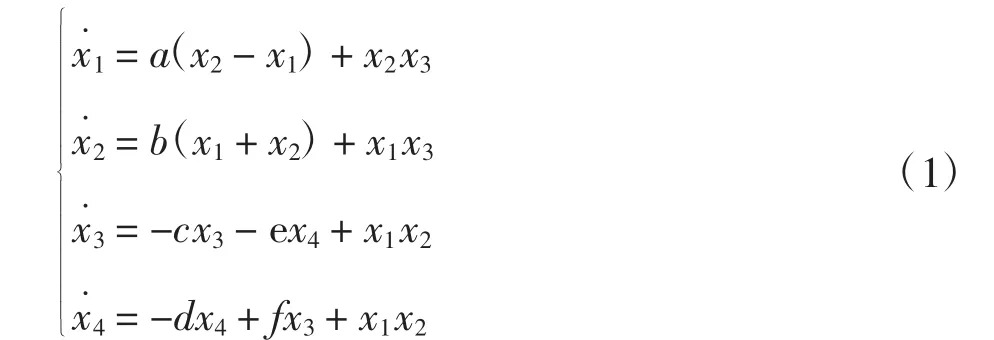
当取 a=50,c=13,d=8,e=33,f=30,b∈[15.425,27]时,系统是超混沌的,其最大的2个正的Lyapunov指数大约为13和3左右.
为了数字实现Qi超混沌系统,下面对连续的微分方程离散化.Qi超混沌系统混乱度高,要求采样时间为τ=0.000 01,因而其占用空间比普通混沌和一些超混沌系统的大得多.考虑到离散化精度,资源消耗和生成混沌序列速度等问题,Euler法相对较简单,比较易于实现,且占用资源少[16],因此这里选用Euler法.
对于一阶微分方程Euler法可表示为:
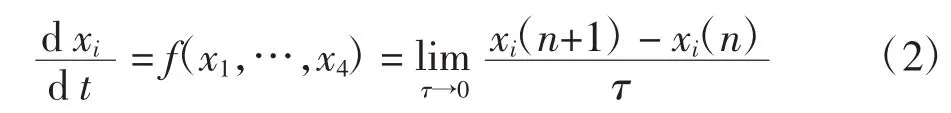
式中:τ为采样时间.对(2)式离散化后的方程为
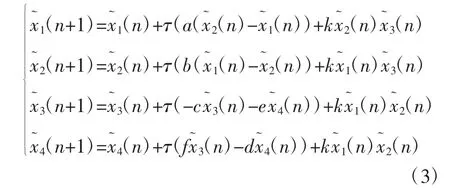
对于(3)式,用Verilog HDL设计Qi超混沌系统,将整个系统划分为若干基本功能模块,主要包括状态机模块、数值计算模块、数值计算控制模块、数据缓存模块、伪随机序列生成模块.超混沌系统的结构框图如图2所示.
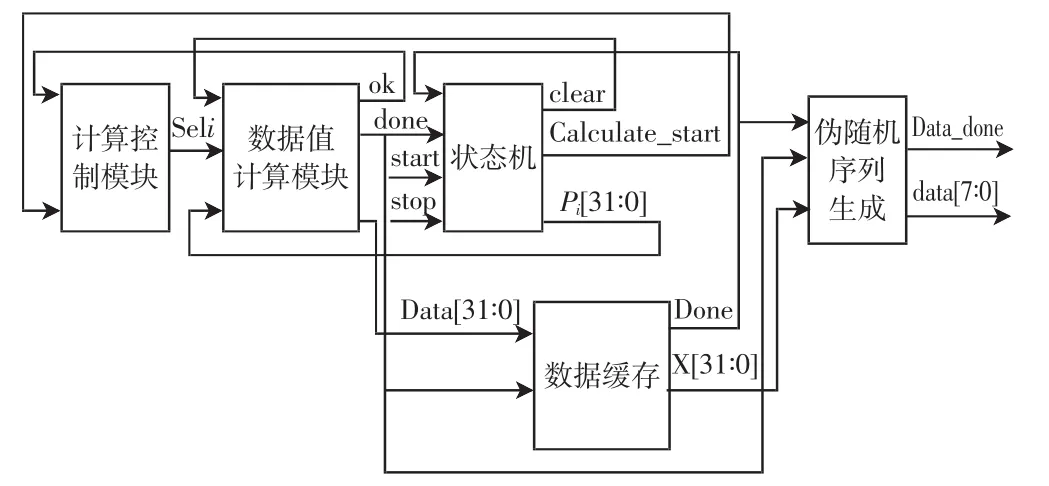
图2 超混沌系统模块结构图Fig.2 Hyperchaos system structure diagram
图2中给出了系统中主要的控制信号及数据流关系.为减少硬件资源的占用,设计中采用了分时复用的思想.数值计算模块例化少量的单精度浮点数乘法器和加法器构造一个方程计算模型,状态机模块在不同的状态向数值计算模块赋予不用的系数和状态变量值,从而完成4个方程的顺序计算.
为了简化系统结构图,对部分信号进行了整合,现作解释说明.Seli代表sel1,sel2,sel3,输出到数值计算模块控制浮点数乘法器、加法器有序执行.done:数值计算完成标志;start,stop:开始和停止控制,由外部按键控制;Data:数值计算结果;Pi代表信号 p1,p2,p3,i1,i2,i3,i4,是系统方程的系数及状态变量,它们的位宽度均为32位.Calculate_start:计算开始控制信号;clear:清零;X 代表 x1,x2,x3,x4,4 个状态变量的迭代结果,数据位宽度为32位;Done:数据缓存完成标识;data:伪随机序列.
(1)状态机模块.时序控制模块为数值计算模块、数据缓存等模块提供时序控制信号,以协调各模块有序工作,同时为数值计算模块提供初始值和每次迭代的结果.本文根据(3)式设计状态机实现时序控制.状态机流程如下:
S0:将 x1,x2,x3,x4的初始值写入状态寄存器.
S1:将赋予 p1,p2,p3及状态变量 x1,x2,x2,x3赋予i1,i2,i3,i4输出到计算模块,计算模块开始执行 done 信号有效时进入下一个状态.
S2:将赋予 p1,p2,p3及状态变量 x1,x2,x1,x3赋予i1,i2,i3,i4输出到计算模块,计算模块开始执行 done 信号有效时进入下一个状态.
S3:将赋予 p1,p2,p3及状态变量 x3,x4,x1,x2赋予i1,i2,i3,i4输出到计算模块,计算模块开始执行 done 信号有效时进入下一个状态.
S4:将赋予 p1,p2,p3及状态变量 x3,x4,x1,x2赋予i1,i2,i3,i4输出到计算模块,计算模块开始执行 done 信号有效时进入下一个状态.
S5:当Done有效时,从数据缓存模块中读取4次的计算结果并写入状态寄存器中,并进入状态S1.
(2)数据缓存模块.该模块存储数值计算模块的计算结果,done有效时将计算结果寄存,在完成4次结果的寄存后即完成了离散化的超混沌系统的一次迭代,将本次迭代的结果由Done信号控制返回状态机模块.
(3)数值计算模块.数值计算模块的结构图如图3所示.

图3 数值计算模块结构图Fig.3 Calculation structure
该模块调用了IP核中32位的单精度浮点数乘法器和加法器,共例化了4个乘法器和2个加法器来构建一个方程模型.模块中的sel1,sel2,sel3信号来自计算控制模块,控制各乘法器和加法器有序执行.参数输入信号:p1,p2,p3分别代表方程中的系数输入端口;i1,i2,i3,i4分别代表状态变量输入端口,它们由状态机模块在不同的状态给出每个方程的系数和状态变量值.
(4)伪随机序列生成模块.该模块首先舍去超混沌系统前50次迭代的值,以消除初值影响.IEEE-754单精度浮点数格式为32位,如图4所示.

图4 单精度浮点数格式Fig.4 Single precision floating-point format
其中第 31 位(S)为符号位,1:负;0:正.30-23 位(E)为阶码位.22-0位(F)为尾数位.根据单精度浮点数的特点,取尾数部分位相异或即可得到一定长度的伪随机序列.设混沌系统第k次迭代的结果为x1(k),x2(k),x3(k),x4(k),x5(k),其宽度均为32位.截取变量x1(k),x2(k),x3(k),x4(k),x5(k)的尾数部分数据,分别记为 m1,m2,m3,m4.设置起始位为第 i位,终止位为第 j位,那么截取数据位长度为j-j+1.根据以下规则输出伪随机序列.

则可得伪随机序列{…,s1(k),s2(k),s3(k),…}.尾数部分抽取的位数可以任意设定,本伪随机序列生成模块抽取尾数部分八位则超混沌系统迭代一次可以产生24位伪随机序列,从而利用了高维混沌的特点可有效地减少混沌系统的迭代次数,提高了伪随机序列产生的效率.
1.2.2 FIFO寄存器模块
先入先出寄存器调用自IP核,可实现数据的缓存或高速异步数据的交互.对于数据计算模块高速产生的数据可以存入先入先出寄存器中,再由数据发送模块以一定的波特率读出并发送.本设计中例化了一个深度为2 048,宽度为8位的FIFO.空标志位有效时,向FIFO中写数据,满标志位有效时,系统停止写数据,并开始读出由数据发送模块发送.该FIFO可缓存16 384位的二进制伪随机序列.
1.2.3 FIFO控制模块
FIFO控制模块用于控制FIFO的读写数据及串口发送模块使能.当FIFO寄存器为空时,FIFO控制模块发出写请求,将超混沌模块的计算结果写入FIFO中.写满时其状态标志位变高,接着发送读请求,同时使串口发送模块的发送使能有效,开始读取并发送数据,由发送完成标志信号控制下一个要发送数据的读取.当空标志位重新为高时,停止读数据和,发送使能拉低.并发出写请求,重新向FIFO中写数据.
1.2.4 数据发送模块
数据发送模块负责FPGA硬件系统与PC机的数据通信,由硬件描述语言编程实现串口数据发送.数据发送模块的结构图如图5所示.发送数据的波特率设置为115 200 bps,发送一次数据包含1位起始位,8位数据位,1位停止位.串口发送模块包含2个主要部分波特率生成模块及数据发送模块.波特率生成模块基于查找表和分频计数器实现.

图5 数据发送模块结构图Fig.5 Data sent module structure
2 系统仿真及硬件实现结果
经QuartusII编译后得到的该伪随机数发生器资源消耗情况如表1所示.

表1 系统资源消耗Tab.1 System resource consumption
由表1可以看出,由于采用了分时复用的思想,系统占用资源相对较少,并且有较高的工作时钟频率,系统在140 MHz下可稳定工作.
利用Modelsim对工程进行仿真,得到的时序仿真结果如图6所示.

图6 时序仿真结果Fig.6 Timing simulation results
由图6仿真结果可以看出,本系统可以实现将超混沌系统产生的伪随机序列通过串口发送模块将数据发出.将仿真所得超混沌系统迭代的数据导出到Matlab可得混沌吸引子的相位图如图7、图8所示.
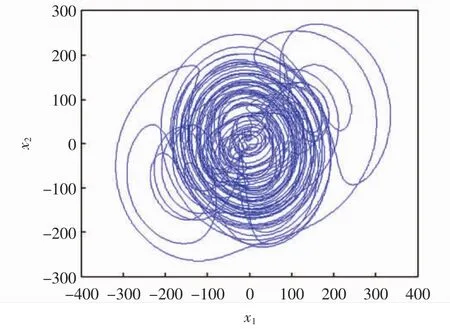
图7 x1-x2相位图Fig.7 x1-x2phase diagram

图8 x1-x3相位图Fig.8 x1-x3phase diagram
由图7和图8可以看出,该基于FPGA设计的超混沌系统可以正确地实现离散化混沌系统的迭代计算,所得相位图与Matlab仿真结果一致.
在确定时序仿真结果无误后,将程序下载到EP4CE15F17C8型FPGA开发板.将FPGA通过串口与计算机相连.计算机端接收到的伪随机序列如图9所示.
从图9实验结果可以看出,基于FPGA硬件平台设计的伪随机数发生器能够产生伪随机序列,并能实现与计算机进行数据通信.
3 伪随机序列的分析与测试
3.1 速度分析
经过modelsim仿真可知,在取尾数部分8位的情况下,系统每隔47个时钟周期产生1个8位比特数据,当工作频率为50 MHz时,该系统产生伪随机序列的速率为8×50/47=8.5 Mbps;当工作频率为140 MHz时,系统产生伪随机序列的速率为8×140/47=23.8 Mbps,可以满足大多数场合的加密需求.
3.2 统计测试
美国国家标准技术局(NIST)设定了15个测试以检验一个随机或伪随机发生序列的统计特性[17].根据SP800-22标准,每项测试结果都用P值表示,如果测试结果的P值大于之前设定的阈值则可认为该项测试通过,反之则不通过.现对计算机端接收到的伪随机序列进行测试,测试的伪随机序列位长度为1.6×107bits,默认设置α=0.01.测试结果如表2所示.
从表2测试结果看出,15项测试的P值均大于设定的阈值,表明本文设计的伪随机数发生器能够产生性能良好的伪随机序列.

表2 NIST测试结果Tab.2 NIST test results
4 结 语
本文针对基于超混沌的伪随机数发生器占用资源高,迭代次数多等问题,基于Qi超混沌系统设计了一种32位单精度浮点数伪随机数发生器.采用分时复用的思想以节省系统资源占用,并且利用高维混沌及计算机浮点数格式的特点,可以有效地减少迭代次数.并采用Verilog HDL在FPGA硬件平台构建了超混沌系统模块、FIFO模块以及数据发送模块,实现了伪随机数发生器的设计.从仿真结果可以看出,该伪随机数发生器占用资源少,产生伪随机序列的速率最高为23.8 Mbps.并且对FPGA硬件平台产生的伪随机序列进行了NIST测试,结果表明该伪随机数发生器产生的二进制序列具有很好的伪随机特性,具有一定的实际应用价值.
[1]禹思敏.混沌系统与混沌电路:原理、设计及其在通信中的应用[M].西安:西安电子科技大学出版社,2011:10-11.YU S M.Chaotic System and Chaotic Circuit:Principle,Design and Its Application in Communication[M].Xi′an:Xi′an University of Electronic Science and Technology Press,2011:10-11(in Chinese).
[2]刘玉民,张雨虹,姚明林.基于FPGA的混沌信号发生器的设计与实现 [J].计算机工程与设计,2010,31(18):3972-3974.LIU Y M,ZHANG Y H,YAO M L.Design and implementation of chaotic signal generator based on FPGA[J].Computer Engineering and Design,2010,31(18):3972-3974(in Chinese).
[3]张丽姣,闵乐泉,韩双霜.二维新混沌系统和伪随机数生成器的设计[J].计算机工程与设计,2014,35(4):1178-1182.ZHANG L J,MIN Y Q,HAN S S.Design of two-dimensional new chaotic system and pseudo-random number generator[J].Computer Engineering and Design,2014,35(4):1178-1182(in Chinese).
[4]刘沛华,鲁华祥,龚国良,等.基于FPGA的高速任意分布伪随机数发生器[J].应用科学学报,2012,30(3):306-310.LIU P H,LU H X,GONG G L,et al.High-speed arbitrary distributed pseudo-random number generator based on FPGA[J].Journal of Applied Sciences,2012,30(3):306-310(in Chinese).
[5]孙克辉,叶正伟,贺少波.混沌伪随机序列发生器的FPGA设计与实现[J].计算机应用与软件,2014,31(12):7-11.SUN K H,YE Z W,HE S B.Design and implementation of chaotic pseudo-random sequence generator based on FPGA[J].Computer Applications and Software,2014,31(12):7-11(in Chinese).
[6]SHAH Divya K,CHAURASIYA Rohit B.FPGA implementation of fractional-order chaotic systems[J].International Journal of Electronics and Communications,2017,78:1-13.
[7]黄沄,张鹏,赵卫峰.一个新的四翼超混沌系统及其FPGA实现 [J].西南大学学报:自然科学版,2013,35(6):127-130.HUANG Y,ZHANG P,ZHAO W F.A new four-wing hyperchaotic system and its FPGA implementation[J].Journal of Southwest University:Natural Science Edition,2013,35(6):127-130(in Chinese).
[8]刘强,方锦清.基于FPGA技术的混沌加密系统研究[J].物理学报,2012,61(13):78-83.LIU Q,FANG J Q.Research on chaotic encryption system based on FPGA technology[J].Journal of Physics,2012,61(13):78-83(in Chinese).
[9]CHEN Zengqiang,YANG Yong,QI Guoyuan,et al.A novel hyperchaos system only with one equilibrium[J].Physics Letters A,2007,360(6):696-701.
[10]QI Guoyuan,WANG Zhonglin,GUO Yanling.Generation of an eight-wing chaotic attractor from QI 3-D four-wing chaotic system[J].International Journal ofBifurcationandChaos,2012,22(12):1250287-1250295.
[11]涂光友,何波.基于时空混沌的伪随机数发生器设计[J].计算机应用,2013,33(12):3499-3502.TU G Y,HE B.Design of pseudo-random number generator based on spatiotemporal chaos[J].Computer Application,2013,33(12):3499-3502(in Chinese).
[12]盛利元,刘念,曹莉凌.一种混沌伪随机序列发生器的FPGA 实现[J].郑州大学学报:工学版,2008,29(1):44-47.SHENG L Y,LIU N,CAO L L.Realization of a chaotic pseudo-random sequence generator based on FPGA[J].Journal of Zhengzhou University:Engineering Science Edition,2008,29(1):44-47(in Chinese).
[13]曹骝,茅耀斌,刘文波,等.时空混沌伪随机比特发生器及其 FPGA 实现[J].系统工程与电子技术,2008,30(9):1606-1610.CAO L,MAO Y B,LIU W B,et al.Time-space chaotic pseudo-random bit generator and its FPGA implementation[J].Systems Engineering and Electronics,2008,30(9):1606-1610(in Chinese).
[14]QI Guoyuan,WYK M A V,WYK B J V,et al.On a new hyperchaotic system[J].Physics Letters A,2008,372(2):124-136.
[15]QI Guoyuan,WYK Michael Antonie van.A new hyperchaotic system and its circuit implementation[J].Chaos Solitons and Fractals,2009,40(5):2544-2549.
[16]周武杰,禹思敏.基于IEEE-754标准和现场可编程门阵列技术的混沌产生器设计与实现[J].物理学报,2008,157(8):4738-4746.ZHOU W J,YU S M.Design and implementation of chaotic generator based on IEEE-754 standard and field programmable gate array technology[J].Journal of Physics,2008,157(8):4738-4746(in Chinese).
[17]RUKHIN Andrew,SOTO Juan,NECHVATAL James,et al.A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications,SP800-22rev1a[S].Gaithersburg:National Institute of Standards and Technology,2010.
