陶瓷3D打印机结构设计与运动学分析

丁承君，吴 畏，朱智辉

（河北工业大学 机械工程学院，天津 300401）

目前，市面上陶瓷3D打印机的喷头结构基本上采用活塞式挤出结构.周婧等[1-2]对活塞式挤出系统进行仿真分析与研究，利用流体分析软件对挤出头出口截面的流速和内部压力场进行数值模拟，对挤出头内部流道的几何形状进行设计，找出了4种不同内部流道的压力场和出口流速分布规律，但是该结构形式不能够满足打印过程持续进料的刚性需求.张利敏[3]在并联机构刚体动力学模型基础上，提出一种基于支链的动力学性能评价指标，该指标可以完整揭示机构产生奇异位型的条件.梁香宁等[4]对Delta机构进行分析，建立了基于动静平台之间的约束方程，分析了Delta机器人的工作空间，利用VC++和OPenGL开发了基于Windows平台的机器人运动学可视化仿真软件.赵杰等[5]运用空间几何学及矢量代数的方法建立了三自由度并联机器人的简化运动学模型，求解运动学正解，回避了运动学多解取舍的问题，可直接获得工作空间内满足运动学连续性的合理解.石志新等[6]应用方位特征集方法，综合了一批满足功能要求的并联机构，从中选取一种具有开发潜力的并联机构，结合实例给出了优选机构的位置正逆解方程.为实现较高速、较平稳的打印，本文设计一款采用并联结构、可持续进料的打印机，对整机机体进行位置正逆解、速度及加速度分析，利用ADAMS软件进行算例仿真分析，验证数学模型的正确性，保证打印喷头运动过程的平稳.

1 陶瓷3D打印机结构总述

本陶瓷3D打印机机体采用Delta结构，如图1所示.主动臂的驱动部分采用柔性带和带轮组成的两级带传动，省去了传动的减速器结构，减轻了整机重量，而且价格便宜，传动平稳，有效减小了驱动过程中的振动.浆料由进料口通过气压压入料筒，通过安装在静平台上方的电机旋转伸缩杆和与伸缩杆连接的螺杆的旋转作用，将持续进入料筒的浆料不间断地从喷头内挤出，从而实现持续供料、不间断打印的目的[7].

图1 打印机整机结构Fig.1 Printer machine structure

2 打印机体位置反解

2.1 位置反解

由于中间伸缩杆不会影响喷头的打印精度，在运动学分析时将其省去.打印机的3个主动臂与3个从动臂够成3个支链，为方便研究，将其中1条主动臂和1条从动臂构成的单支链结构拆离出来分析，其示意图如图2所示[8-13].

图2 单支链结构Fig.2 Single branched chain structure

在静平台中心处建立静坐标系O-XYZ，在动平台中心处建立动坐标系O′-X′Y′Z′，一条主动臂与静坐标系O-XYZ的X轴重合，Z轴垂直于静平台向上.其中：主动臂|AiBi|=L1；从动臂|BiCi|=L2；主动臂在静坐标系中与 X 轴的夹角 αi（i=1，2，3）分别为 0°、120°、240°；主动臂的摆角为 θi（i=1，2，3）；静平台外接圆的半径为R；动平台外接圆的半径为r.

在静坐标系O-XYZ中有如下关系[14-16]：

式中：Ai=Rcos αi+L1cos θicos αi（i=1，2，3）；Bi=Rsin αi+L1cos θisinαi（i=1，2，3）；Ci=-L1sin θi（i=1，2，3）.

OCi（i=1，2，3）在动坐标系O′-X′Y′Z′中可表示为：

Ci（i=1，2，3）在静坐标系O-XYZ中的坐标向量为：

则从动臂BiCi（i=1，2，3）在静坐标系O-XYZ中的坐标为：

式中：Di=x+rcosαi-（Rcosαi+L1cos θicos αi）（i=1，2，3）；Ei=y+r sin αi-（R sin αi+L1cos θisin αi）（i=1，2，3）；Fi=z+L1sinθi（i=1，2，3）.

式中：Gi=x+rcosαi-（Rcosαi+L1cosθicosαi）（i=1，2，3）；Hi=y+r sin αi-（Rsinαi+L1cosθisinαi）（i=1，2，3）；Si=z+L1sinθi（i=1，2，3）.

将式（7）进行化简得到：Iicos θi-Jisin θi-Ki=0

式中：Ii=2L1[（x+rcosαi-R cos αi）cos αi+（y+rcosαi-R sinαi）sinαi]；Ji=2L1z；Ki=（x+rcosαi-Rcosαi）2+（y+

根据倍角公式和打印机的装配关系，位置反解为：

2.2 位置反解验证

本文选取的机体尺寸参数为：R=205 mm，r=40 mm，L1=140 mm，L2=510 mm.位置反解就是给定动平台1个位置，求得3个驱动转角的大小.现对动平台中心施加螺旋曲线的驱动：

将式（9）带入反解方程（8），可求得 3个转角角度（rad）与时间（s）的关系，仿真时间设置为20 s，其3个转角随时间变化的关系曲线如图3所示.

图3 驱动角变化曲线Fig.3 Changing curve of driven angle

由图3可知，在运动过程中3个转角曲线平顺光滑，没有突兀点，故位置逆解方程正确.3个驱动转角能够顺畅地控制末端的轨迹，实现良好的打印效果，在打印过程中不会出现奇点，保证打印的精确性.

3 打印机体位置正解

3.1 位置正解方程

位置正解就是已知输入的3个驱动转角的大小，求得动平台中心的位置.该陶瓷打印机为典型的并联机构，相对于串联机构而言，并联机构的位置逆解较容易而正解较难.目前，通常有2种方法求得并联机构的正解：一种是数值法，另一种是几何法.几何法需复杂的几何数学推导，正解不易求出，故采用数值法求解[17-18].

式中：

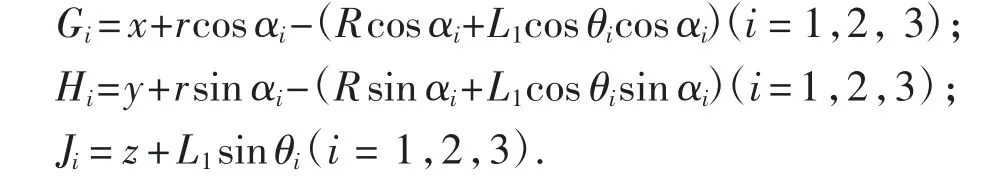
式（10）为1个含有3个未知数、3个方程的非线性方程组，使用Matlab采用最小二乘法，输入3个主动臂的转角值，即可求得动平台中心的位置.

3.2 位置正解验证

首先，设定末端的运动轨迹为如式（9）所示的螺旋曲线，按照已经验证的位置逆解方程求得3个驱动转角θi（i=1，2，3）与t时间的关系，将该关系式带入正解方程（10），仿真时间设置为20 s，求得在位置正解方程下的末端位置x、y、z与时间t的曲线.若同样为该螺旋线的话，位置正解即验证正确.利用ADAMS软件的ADAMS/Processor中的曲线处理工具得到末端位置位移（mm）与时间（s）的曲线，如图4所示.

图4 末端运动状态Fig.4 State of terminal motion

由图4可知，动平台中心处X、Y、Z 3个方向的位移曲线均光顺没有突兀点，Z轴方向为竖直，其轨迹线为螺旋曲线，符合方程（9），故位置正解得到验证.

4 速度、加速度分析

4.1 速度求解

对于 n 自由度机器人，关节变量 q=[q1，q2，…，qn]T，当关节变量为转动关节时，qi=θi；当关节变量为移动关节时，qi=di；由Xn=Xn（q）可得：

式中：J（q）为（6× n）的偏导数矩阵，称为 n自由度机器人速度雅克比矩阵.

在该打印机结构中，关节变量为转动关节，将式（11）对时间求导得：

同样，取打印机3条支链中的1条进行分析，如图 1（a）所示.

令 Si=BiCi，则 Si=OO′-（OAi+AiBi+CO′），在每条主动臂与静平台连接点Ai处建立坐标系{Ti}，{Ti}的X、Y、Z 3坐标轴的方向与固定坐标系X、Y、Z 3坐标轴的方向相同，则

故输入3个驱动角速度θ˙i（i=1，2，3），通过式（17）即可求得动平台末端的速度.

4.2 加速度求解

速度求解完后，加速度求解就变得十分简单，对速度方程求导即可.

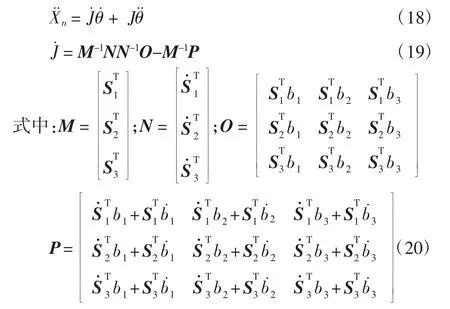
则输入3个驱动角加速度θ¨i（i=1，2，3），通过式（20）即可求得动平台末端的加速度.

4.3 速度、加速度算例验证

在ADAMS中，对3个驱动角的旋转运动副添加的速度驱动分别为加速度驱动为仿真时间设置为20s，速度与加速度驱动曲线如图5所示.利用ADAMS/Processor中的曲线处理工具箱，求得末端的速度与加速度曲线，如图6所示.由图6可知，末端在X、Y、Z 3个方向上的最大速度分别为31、18、38 mm/s，最大加速度分别为30、45、45 mm/s2，其曲线均光顺无突兀点，可见打印机喷头末端的运动较为平稳，能够实现较精确的打印效果.

图5 速度、加速度驱动曲线Fig.5 Speed and acceleration curves of driven angle

图6 末端速度、加速度曲线Fig.6 Speed and acceleration curves of terminal

5 结 语

本文基于Delta结构设计了一款可实现持续进料、连续打印的陶瓷3D打印机，对陶瓷打印机的机体进行了运动学、速度和加速度分析，建立位置正逆解和速度、加速度方程，并结合具体参数进行算例仿真分析，验证了运动学、速度和加速度数学模型的正确性.在本文设定的仿真条件下，打印终端在X、Y、Z 3个方向上的最大速度分别为 31、18、38 mm/s，在 X、Y、Z 3 个方向的最大加速度分别为30、45、45 mm/s2，并且在运动过程中速度、加速度没有突变，实现了平稳打印.

[1]周婧，段国林，卢林.陶瓷浆料微流挤压成型关键问题研究[J].中国机械工程，2015，26（22）：3097-3101.ZHOU J，DUAN G L，LU L.The key problem research of ceramic slurry microflow extrusion[J].The Chinese Mechanical Engineering，2015，26（22）：3097-3101（in Chinese）.

[2]周婧，段国林，金星.义齿陶瓷浆料微流挤压成型头研究[J].机械设计，2016，33（2）：61-67.ZHOU J，DUAN G L，JIN X.The research of ceramic slurry microflow extrusion head[J].The Mechanical Design，2016，33（2）：61-67（in Chinese）.

[3]张利敏.基于动力学指标的Delta高速并联机械手集成优化设计方法研究[D].天津：天津大学，2011.ZHANG L M.Integrated optimization based on dynamic index of the Delta high-speed parallel manipulator design method research[D].Tianjin：Tianjin Universcity，2011（in Chinese）.

[4]梁香宁，牛志刚.三自由度Delta并联机器人运动学分析及工作空间求解[J].太原理工大学学报，2008，39（1）：93-96.LIANG X N，NIU Z G.3-D of Delta parallel robot kinematics analysis and working space to solve[J].Journal of Taiyuan University of Technology，2008，39（1）：93-96（in Chinese）.

[5]赵杰，朱延河.Delta型并联机器人运动学正解几何法[J].哈尔滨工业大学学报，2003，35（1）：25-27.ZHAO J，ZHU Y H.Delta type parallel robot kinematics solution is geometric method[J].Journal of Harbin Institute of Technology University，2003，35（1）：25-27（in Chinese）.

[6]石志新，叶梅燕，毛志伟.5-5型并联机器人位置正解的简单算法[J].农业机械学报，2016，47（3）：395-404.SHI Z X，YE M Y，MAO Z W.Simple algorithm of parallel robot position positive solutions[J].Journal of Agricultural Machinery，2016，47（3）：395-404（in Chinese）.

[7]丁承君，吴畏，朱智辉.陶瓷3D打印机喷头结构设计与仿真分析[J].天津工业大学学报，2017，36（4）：84-88.DING C J，WU W，ZHU Z H.Structure design and simulation analysis of ceramic 3D printer nozzle[J].Journal of Tianjin Polytechnic University，2017，36（4）：84-88（in Chinese）.

[8]WANG J S，LIU X J.Analysis of a novel cylindrical 3-DOF parallel robot[J].Robotics and Autonomous System，2003，42：31-46.

[9]杨延力，刘安心，罗玉峰.机器人机构拓扑结构设计[M].北京：科学出版社，2012.YANG Y L，LIU A X，LUO Y F.Robot Mechanism Topological Structure Design[M].Beijing：Science Press，2012（in Chinese）.

[10]李秦川.对称少自由度并联机器人型综合理论及新机型综合[D].秦皇岛：燕山大学，2003.LI Q C.Symmetrical type less degrees of freedom parallel robot integrated theory and new models[D].Qinhuangdao：Yanshan University，2003（in Chinese）.

[11]赵铁石，高英杰，杨铁林.混合型四自由度并联平台机构及其位置分析[J].光学精密工程，2009，8（1）：42-45.ZHAO T S，GAO Y J，YANG T L.Hybrid four DOF parallel platform mechanism and its location analysis [J].Optical Precision Engineering，2009，8（1）：42-45（in Chinese）.

[12]金琼，杨延力，刘安心.基于单开链单元的三平移一转动并联机器人机构型综合及机构分类[J].中国机械工程，2009，12（9）：1038-1043.JIN Q，YANG Y L，LIU A X.Based on single open chain unit of three translational one rotation parallel robot mechanism type comprehensive and classification[J].The Chinese Mechanical Engineering，2009，12（9）：1038-1043（in Chinese）.

[13]黄真，孔令福，方跃法.并联机器人机构学理论及控制[M].北京：机械工业出版社，2007.HUANG Z，KONG L F，FANG Y F.Parallel Robot Mechanism Theory and Control[M].Beijing：Mechanical Industry Press，2007（in Chinese）.

[14]FENG G.Physical model of the solution space for 3-DOF parallel planar manipulations[J].Mechanisms and Machine Theory，2006，31（2）：161-171.

[15]CONTE J，SANTOLARIA J.Identification and kinematic calculation of laser tracker errors[J].Procedia Engineering，2013，63：379-387.

[16]LI J F，CHEN W H，LIU D Z.Inverse kinematic and dynamic analysis of a 3-DOF parallel mechanism[J].Chinese Journal of Mechanical Engineering，2003（1）：54-58.

[17]MERLET J P.Parallel Robot[M].Netherlands：Springer，2006.

[18]HUANG T，LI M，ZHAO X M.Conceptual design and dimensional synthesis for a 3-DOF module of trivariant：A novel 5-DOF reconfigurable hybrid[J].IEEE Transactions on Robotics，2005，21（3）：449-456.