基于CFD灌溉机井管道液相流场的数值模拟
2018-03-05王萍,杨超
王 萍 ,杨 超
(1.天津工业大学电气工程与自动化学院,天津 300387;2.天津工业大学电工电能新技术天津市重点实验室,天津 300387)
随着仪表技术的发展,超声波流量计开始广泛应用于农用灌溉领域,其优点在于运行稳定,计量精确度高,无压力损失,并且能够进行非接触测量[1].当前,超声波流量计研究领域的重点方向为传感器探头制作工艺、信号提取与处理的准确性以及低功耗.邱立存等[2]提出数字平均技术可使测量回波信号得到加强,提高测量精度;贺胜等[3]则对超声波流量计的最优声道位置选取进行研究.但对于流体流场的变化与分布对流量计测量精度的影响研究较少.实际生产中,灌溉机井出水管道属于非充分发展流场,这对时差法超声波流量计的测量精度产生很大干扰.本文从理论上分析机井管道非充分发展管流情况下的流体速度分布特性,采用计算流体力学数值模拟与实流测试相结合的方法,确定三维流场的数学模型,探究流场分布规律,进而提出平均流速修正公式,通过实验验证,提高流量计的测量精确度.
1 时差法流量测量原理
时差法测量的原理是利用超声波脉冲在流体中顺流和逆流传播过程中的时间差来计算流体流速,再将流速进一步换算成流量,如图1所示.
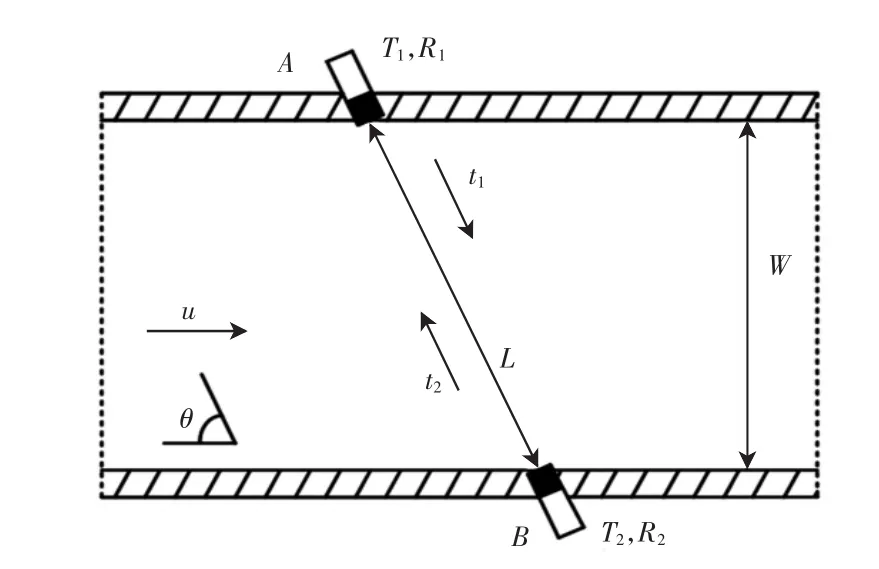
图1 超声波流量检测原理图Fig.1 Ultrasonic flow detection schematics
2个超声波换能器被斜向对称安装在被测量管道两侧,换能器 A、B 同时作为发生器(T1,T2)和接收器(R1,R2)交替工作,超声波声速为C,水流速度为u.设超声波顺流传播时间为t1,逆流传播时间为t2,流体流速的超声波束传播方向分量为ucos θ,W为截面宽度,在本例中即为圆管直径D.由此导出t1与t2的表达式为:

进而推导出流体流速表达式为:

管道内流量等于流体平均流速乘以管道截面积,计算表达式为:

由于W等于直径D,所以流量进一步表示为:
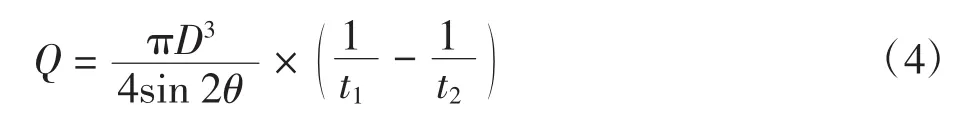
在天津工业大学工程实训中心流量测量实验室采用既有时差法流量计进行实际流速测量,通过调节变频电机的转速将水流初始速度设置为2.5 m/s,选取测量管道为90°弯管的机井出水管道模型.表1所示为出水管位置6D处测量速度的3次典型值.

表1 位置6D处水平轴截面的速度数据Tab.1 Velocity data of 6D horizontal axis section
由表1可以看出,在实际工况环境中,稳定状态下的流体流经90°弯管后,在流量计传感器安装位置处测得流体流动速度变小.为提高时差法流量计的测量精度,本文建立管道内三维流场的数学模型,对机井管道非充分发展管流情况下的流体速度分布特性进行分析.
2 流体力学求解
2.1 几何模型的建立
本文选取某水泵公司某型号潜水泵为标准建立模型,其流量为70 m3/h,扬程22 m,输水管径为100 mm,经计算流速约为2.5 m/s.利用Gambit软件建立带90°弯管的机井出水管道模型,模型取竖直方向长度为20倍管径,水平方向长度为10倍管径,弯径曲率为1.5,所建模型如图2所示.为了得到更好的收敛性与精确度,面网格采用钱币画法,在弯道处加密网格,网格总数量为9.63×105个.
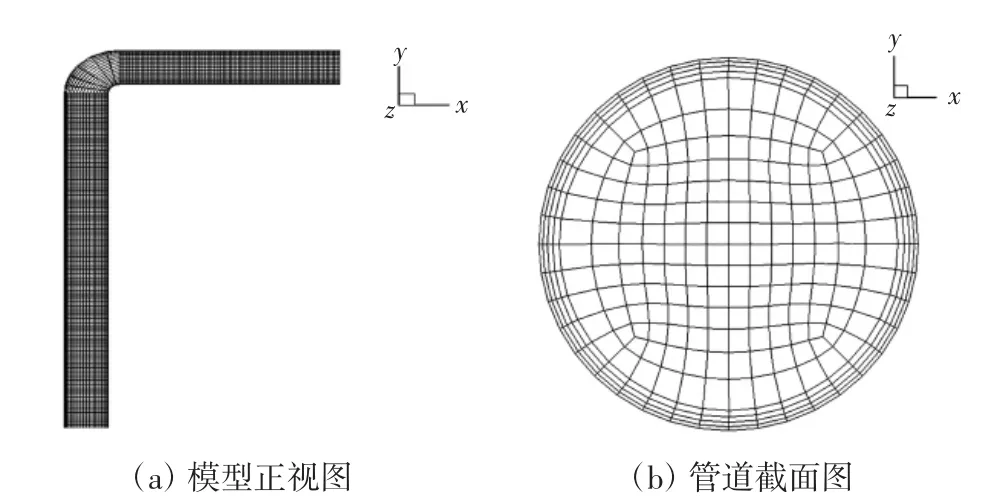
图2 网格划分图Fig.2 Diagram of meshing
2.2 设定边界条件和流动区域
选择入口类型为VELOCITY_INLET,出口设置为OUT_FLOW,其余管道壁面默认为固壁WALL.设定流动区域为机井出水管道的整个几何实体,类型为“FLUID”.最后,将网格文件保存输出.
2.3 利用Fluent求解器求解
将网格文件读取到Fluent软件中进行三维求解计算.由于流体为不可压缩粘性流体,故求解器选择非耦合隐式算法.通过对连续方程和N-S方程进行时均化处理,得到在笛卡尔坐标下的定常、绝热、粘性、不可压缩流体流动的控制方程[4].
连续性方程:

运动方程:
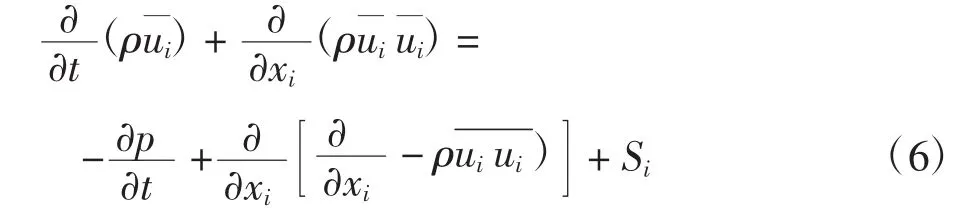
湍流数值模拟采用标准k-ε湍流模型来描述流体流动,该模型的湍动能k和耗散率ε的运输方程为:

式中:Gk为由于平均速度梯度引起的湍动能产生项;Gb为由浮力引起的湍动能产生项;YM为可压速湍流脉动膨胀对总的耗散率的影响.湍流黏性系数μt=ρCμk2/ε,模型常数 C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0,σε=1.3[5-6].
本次试验所选流体为液体,给定初始速度为2.5 m/s,温度设定为20℃,密度为998.2 kg/m3,运动黏度为1.003 g/(m·s).经计算,管道雷诺数大于临界值2 000,流体流动属于湍流,由经验公式计算出湍流强度为0.033 8%,圆柱管道水力直径即为管径DH=0.1 m.考虑到潜水泵电机在持续做功克服重力,所以无需考虑重力作用.
2.4 残差图分析
初始化流场后,对流场模型进行迭代计算,图3所示为模拟系统残差图.

图3 系统残差图Fig.3 System residual plots
由图3可以看出,迭代次数达到195次时模型基本收敛,说明在高雷诺数条件下网格的收敛速度比较快,计算所需的时间较少,基本达到设定条件.
2.5 图形仿真结果
在模型求解过程中,离散方程组采用SIMPLE算法,选择二阶迎风格式进行求解.由于三维的模拟结果不便于观察,所以创建内部XY截面图来查看计算结果,选择三点创建等值面的方式来构建观察面.设定入口水流速度为2.5 m/s时,管道竖直轴截面的模拟云图如图4所示.
由图4可知:

图4 竖直轴截面的流体运动模拟云图Fig.4 Fluid motion simulation nephogram of vertical cross-section
(1)在弯管竖直方向流体入口处,由于流体还未受到弯曲段的影响,图 4(a)所示压力始终平稳,图 4(d)流线排列整齐,流体速度均匀,由于边界层摩擦力的存在,图4(b)靠近管壁处颜色变暗流体速度降低.当流体继续向上运动到弯管附近时,管道外侧的流速开始显著降低,并且越靠近外侧下降幅度越大;在管道内壁速度逐渐增加,在弯管最内侧最大速度达到4.08 m/s,是初始速度的1.63倍.观察弯管附近的压力云图,弯管外侧压力明显大于内侧,这是由于流体进入弯管的离心力所致.由于离心力的作用,在弯管横向段出现二次流,二次流的扰动作用使流体速度提高[7].
(2)观察弯管出口处的速度云图和压力云图可知,流体速度出现分层现象并由内侧到外侧逐渐升高,紧靠管壁内侧最低速度降至1.41 m/s,是初始速度的0.56倍.这种现象是由弯管的特殊结构导致的,流动方向的骤变使管壁内侧流体动能损耗,速度降低,随着相近流体的带动速度逐渐增加.由图4(b)、(c)、(d)可以看出,内侧流速始终小于外侧,呈现出不同流速流体共流的现象[8-9].
由于实际生产中流量计的安装位置位于弯管末端横向管道上,所以取横向管道上弯管90°截面以及2D、4D、6D、8D 4个位置的轴向截面作为观察对象,为了便于观察直接采用isometric视角截取上述5个截面的速度云图进行对比,如图5所示.
由图5可知,随着流体向前流动,二次流现象逐渐减弱,上层速度较高的区域面积逐渐减小,当流体运动到4D长度时中心显示速度最接近初始速度2.5 m/s,但是速度分布仍然不均匀,云图存在较为明显的漩涡,只是强度减弱.对比后4个截面的速度矢量图,如图6所示.

图5 典型位置截面速度云图(m/s)Fig.5 Velocity nephogram of section at typical positions(m/s)

图6 截面速度矢量图(m/s)Fig.6 Velocity vector of different section(m/s)
由图6可知,2种不同流速的区域在相互融合,上层速度逐渐降低,下层速度逐渐升高,并同时向中心区域的初始速度靠拢.
为了更直观对比,分别取横向出水管道竖直轴截面1/4、1/2、3/4处由上及下3条直线上的点绘制出坐标图显示速度的变化,如图7所示.

图7 竖直截面速度曲线Fig.7 Velocity curves of vertical cross-section
由图7可以看出:在横向管道中轴线上,流体在经过弯管达到最大速度峰值后呈下降趋势,在0.4 m附近处达到最小值并逐步上升至初始值2.5 m/s附近.在竖直轴截面上机井出水管道的不同层面以及不同位置的流速差别很大,流体速度分层明显,数值紊乱,对实际的流量计测量造成误差.因此,考虑在机井出水管道的水平轴截面安装流量计,下面采用isometric视角简要分析水平轴截面的流体运动状况,如图8所示.
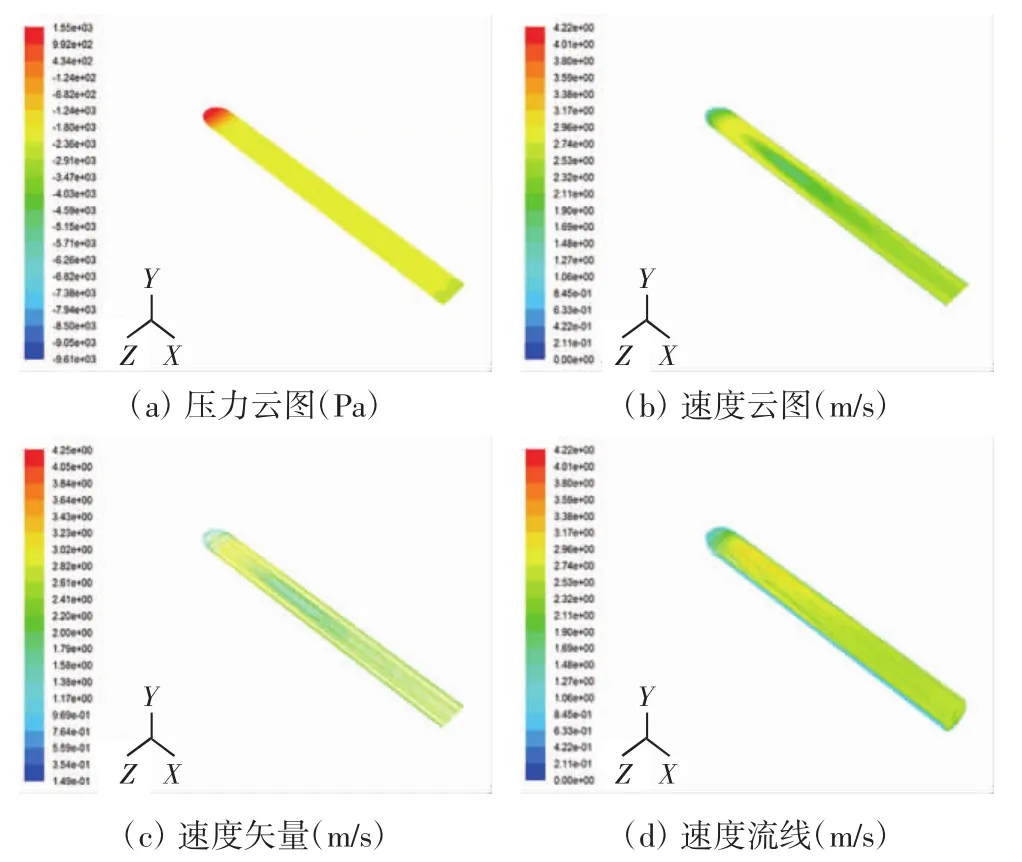
图8 水平轴截面的流体运动模拟云图Fig.8 Fluid motion simulation nephogram of horizontal cross-section
由图8可知,流体流经弯管,在水平轴截面中心区域的流速低于两侧流速,在速度云图上呈现低速漩涡;随着流体继续向前运动,中心区域流速逐渐升高,并与两侧融合接近.分别取水平轴截面由前向后1/4、1/2、3/4处的3条直线描绘速度变化,如图9所示.

图9 水平截面速度曲线Fig.9 Velocity curves of horizontal cross-section
由图9可知,在水平轴截面管道两侧的流体速度变化趋势基本重合.中间区域的流体速度与前文竖直截面分析结果相同,流体速度在流经弯管获得最大值后下降至最小值继而逐渐上升与两侧速度融合,显然这是受到二次流的影响[8-9].
2.6 数值模拟计算流速
通过上述分析,相对于竖直轴截面的流体速度分层且速度不对称分布的情况,水平轴截面的速度分布更适合作为流量计探头安装位置进行流量检测.选取入口速度为2.5 m/s时,在流速相对稳定的6D位置处对水平轴截面进行3点数据统计.在该截面上取一条与管道夹角成60°的切线,将该切线四等分,测量每一段上的3点速度值.V1方向为水流流动方向,将速度矢量投影到水平和垂直2个方向上,如图10所示.
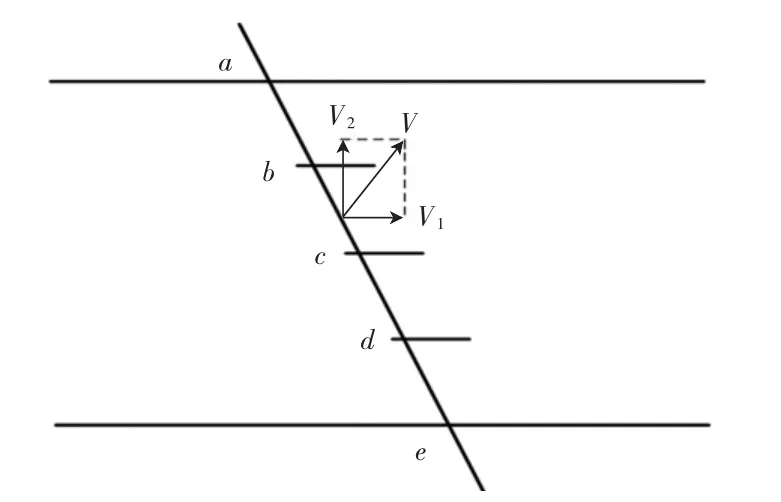
图10 水平轴截面速度矢量俯视图Fig.10 Velocity vector planform of horizontal cross section
在Fluent软件中输入几何模型6D位置处的切线上各数值求解点的X轴、Y轴和Z轴的坐标值,模拟出的流速数据如表2所示.

表2 水平轴截面的速度数据Tab.2 Velocity data of horizontal axis section
表2中的数据为经Fluent软件后处理后得出的数据,如图10所示将声波传播路径等分成4段,分别为 ab、bc、cd、de 段,其后再将每一段分别取其 1/4、1/2、3/4点位置计算出其速度值v以及水平方向速度值v1,这12个点的数据将作为数值模拟数据,与实验室实际测量流速值进行比较,并完成流速数值的校正补偿.
3 流量补偿计算
在实际测量时,超声波接收装置安装在机井出水管水平轴截面的前后两侧,通过对不同层面的流量补偿系数的确定计算出最终的补偿系数[10-15].
超声波顺流与逆流传播时间不同,二者之差Δt为:

由于u cos θ< 表2统计了Fluent模拟条件下来流速度为2.5 m/s时,出水管道水平轴截面上位置6D处测量切线各点水平方向的速度数据.为了提高测量精度,结合既有时差法流量计实验室实流测试数据,分别对该切线4段的中点、1/4点以及3/4点处的速度值进行补偿计算,进而求得最终管道流量补偿值[14].4段中点处的时差之和以及实流测试时传感器接收脉冲所需时差表达式为: 推导出中点处的补偿系数与速度补偿值: 同理,得到表1中每段1/4点处和3/4点处的补偿系数: 由上述3组运算结果可计算得到平均补偿系数与速度补偿值: 经过校正补偿后管道内流体流量为: 通过上述计算可知,当入水速度为2.5 m/s时,实验室传感器所测得的流体速度为2.35 m/s,平均流量为66.4 m3/h,约为CFD模拟所得速度的0.951倍,补偿速度大约为0.12 m/s,即真实流速需要在传感器实测值的基础上增加0.12 m/s.补偿后平均流量为69.8 m3/h,经修正补偿公式计算,测量精确度提升了4.9%. 本文通过建立农用灌溉机井出水管道流体模型,完成了流场分布计算的理论推导,分析得出流体经90°弯管产生的二次流使出水管流场分布急剧紊乱,经对比,选择具有分布对称性的水平横截面作为超声波探头安装位置.为降低非均匀发展的弯管二次流流场对时差法超声波流量计测量精确度的影响,基于本文提出的某型号水泵,结合CFD仿真数据与实验室实际测量数据,提出平均流速修正公式,求解具体情况下的流速与流量补偿系数.结果表明,经补偿后流量计测量精确度提升4.9%.本研究在一定程度上降低了流场分布不均对流量计测量精确度的影响,对现有各种应用在非充分发展流场的时差法超声波流量计的程序编程及流量修正具有参考价值. [1]陈震,范永申,周庆峰,等.常用农业灌溉水表精确性及耐砂耐冻测试评价[J].灌溉排水学报,2015,34(10):19-24.CHEN Z,FAN Y S,ZHOU Q F,et al.Evaluating accuracy and duration sediment of wear test and frozen treatment of agriculture common watermeters[J].Journal of Irrigation and Drainage,2015,34(10):19-24(in Chinese). [2]邱立存,王汝琳.超声波气体流量测量系统的实现[J].传感器与微系统,2006,25(1):47-49.QIU L C,WANG R L.Realization of ultrasonic gas flow measurement system[J].Transducer and Microsystem Technologies,2006,25(1):47-49(in Chinese). [3]贺胜,彭黎辉,仲里敏.基于CFD的超声波流量计最优声道位置研究[J].仪器仪表学报,2009,30(4):852-856.HE S,PENG L H,ZHONG L M.Computational fluid dynamics based sound path optimization for ultrasonic flow meter[J].Chinese Journal of Scientific Instrument,2009,30(4):852-856(in Chinese). [4]NORLI P,LUNDE P,VESTRHEIM M.Investigation of precision sound velocity measurement methods as reference for ultrasonic gas flow meters[J].Rotterdam,Netherlands:IEEE Ultrasonics Symposium,2005,3(2):1443-1447. [5]王萍,万凯.大口径矩形弯管气体流场建模与仿真[J].天津工业大学学报,2013,32(3):82-84.WANG P,WAN K.Modeling and simulation of rectangular pipe with large diameter gas flow[J].Journal of Tianjin Polytechnic University,2013,32(3):82-84(in Chinese). [6]王福军.计算流体动力学分析[M].北京:清华大学出版社,2004:121-125.WANG F J.Computational Fluid Dynamics Analysis[M].Beijing:TsinghuaUniversityPress,2004:121-125(inChinese). [7]饶永超,常凯,王树立,等.90°弯管内流体流动特点数值模拟[J].常州大学学报:自然科学版,2016,28(3):65-69.RAOYC,CHANK,WANGSL,etal.Numericalsimulationof fluidflowcharacteristicin90°bendpipe[J].JournalofChangzhou University:Natural Science Edition,2016,28(3):65-69(in Chinese). [8]ZHAO Z H,FERNANDO H J S.Numerical simulation of scour around pipelines using an Euler-Euler coupled two-phase model[J].Environmental Fluid Mechanics,2007,7:121-142. [9]江山,张京伟,吴崇健,等.基于FLUNET的90°圆形弯管内部流场分析[J].中国舰船研究,2008,3(1):37-41.JIANG S,ZHANG J W,WU C J,et al.Numerical simulation of inner flow in 90°bending duct of circular section based on fluent[J].Chinese Journal of Ship Research,2008,3(1):37-41(in Chinese). [10]吴春华,鲍敏.超声波流量计的弯管误差分析及修正研究[J].机电工程,2015,32(2):175-179.WU C H,BAO M.Bending pipe error analysis and correction of ultrasonic flowmeter[J].Journal of Mechanical&Electrical Engineering,2015,32(2):175-179(in Chinese). [11]BRASSIER P,HOSTEN B,VULOVIC F.High-frequency transducers and correlation method to enhance ultrasonic gas flow metering[J].Flow Measurement&Instrumentation,2001,12(1):201-211. [12]方翔.超声波气体流量计的研制[D].武汉:华中科技大学,2004.FANG X.A thesis submitted in partial fulfillment of the requirements for the degreeofmaster of engineering[D].Wuhan:Huazhong University of Science and Technology,2004(in Chinese). [13]TABIB M V,ROY S A,JOSHI J B.CFD simulation of bubble column:An analysis of interphase forces and turbulence models[J].Chemical Engineering Journal,2008,139(3):589-614. [14]荣双.大口径烟道气体流量测量方法的研究[D].天津:天津工业大学,2016.RONG S.Research on large diameter flue gas flow measurement method[D].Tianjin:Tianjin Polytechnic University,2016(in Chinese). [15]MERIBOUT M,RAWAHI N Z,NAAMANY A M,et al.A multisensor intelligent device for real-time multiphase flow metering in oil fields[J].IEEE Transactions on Instrumentation&Measurement,2010,59(6):1507-1519.


4 结 语
