基于灰色关联-组合赋权的建筑工程项目评标模型研究*

2018-03-03吴夏萍张建坤

项目管理技术 2018年2期

吴夏萍张建坤

(东南大学土木工程学院，江苏南京 210096)

0 引言

随着我国市场经济的不断发展，建筑工程项目的规模越来越庞大，投资额不断增加、建设周期变长、施工条件愈来愈复杂。面对越来越具挑战性的局面，为了使项目达到预期的效果，满足投资各方的利益诉求，招标人需要从众多投标人中挑选出一位最佳的承包人，从而保证工程项目的成本、质量、工期在限定的投资额度和规定的时间期限内达到理想的效果。评标是招投标活动中一个十分关键而又细微的环节，其目的就是从所有投标方案中选择出一位报价合理、质量优良、工期较短、具有良好业绩和管理水平的满意承包人。评标方法作为整个评标过程的核心，选择哪种评标方法直接关系招标人能否成功选出最佳的中标单位，所以要使招投标活动规范化的核心就是要规范和完善评标方法。

我国现阶段采用的评标方法主要有综合评估法、经评审的最低投标价法或法律法规允许的其他评标方法[1]。但这些评标方法主要通过专家的主观评价来确定中标候选人或第一中标人，很难避免主观因素所带来的偏差，易造成评标结果不够公正合理；此外，这些评标方法都没有构建严谨的数学模型，也没有将评标过程中可能存在的模糊性考虑进去[2]。有不少学者通过引入单个数学方法来构建评标模型，如模糊综合评价模型[3]、层次分析法(AHP)评价模型[4]等，虽然这些模型对提高评标方法的科学性起到了一定作用，但是在这些模型中，模糊综合评价模型在确定指标隶属函数的时候，通常把很多本来已经是“白化”的信息进行了模糊化处理，从而导致评标误差；层次分析法评价模型主要是通过专家的经验判断来确定主观偏好系数[5]；这些方法均存在主观因素重、对定量指标缺乏分析等缺点。还有一些学者通过引入两种数学方法构建评标模型，如基于熵权法-灰色关联的评标模型[6]、基于灰色关联-DEA交叉效率模型[7]、基于熵权-TOPSIS的评标模型[8]、基于信息熵和价值工程的评标模型[9]等，虽然这些评标模型的提出都极大地改进了传统评标方法存在的缺陷，但均存在客观性强、无法体现业主的主观偏好等缺陷。为了克服现有评标方法的不足，不少学者开始尝试构建基于三种数学方法的评标模型，将组合赋权的方法引入到评标领域中，如基于模糊物元-综合集成赋权的评标模型[10]、基于组合赋权-TOPSIS的评标模型[5，11]，这些模型的提出大大改进了原有评标方法的不足，提高了评标模型的科学性和准确性。

目前，关于基于灰色关联与层次分析法[12]以及基于灰色关联与熵权法[13-14]来构建评标模型的研究成果有不少，但将这三种数学方法组合起来构建评标模型的研究成果几乎没有。因此本文提出了一种基于灰色关联-组合赋权的评标模型，即通过运用层次分析法确定主观偏好系数，与熵权法所确定的客观权重线性加权得到组合权重，并以此为基准，与灰色关联系数结合起来共同确定灰色关联综合度，通过比较其大小对投标单位进行综合评价。该评标模型结合了灰色关联分析和组合赋权的优点，不仅注重基于专家经验判断的主观权重，而且还重视反映评标指标信息量大小的客观权重，增加了评标的客观性与科学性；而灰色关联系数揭示了各指标之间存在的复杂的隐性关系，提高了评标的准确性和可靠性。最后通过案例分析，对该评标模型的可操作性和实用性进行了验证。

1 建立基于灰色关联-组合赋权评标模型

本文首先参考大量文献建立了建筑工程项目的评价指标体系；其次，提出构建基于灰色关联-组合赋权的评标模型，通过灰色关联系数分析各指标间存在的复杂的隐性关系；再次，利用层次分析法确定指标的主观权重，熵权法确定指标的客观权重，再通过线性加权法确定指标的组合权重；最后，将灰色关联系数与组合权重复合，通过定量的数值来评判投标方案的优劣，从而确定最佳的中标单位。

1.1 建立评价指标体系

本文参考了大量文献[15-18]并结合建筑工程项目的特点，将评价指标体系分为3项一级指标和8项二级指标，见表1。

表1 评标指标体系

(续)

1.2 灰色关联系数分析

评标过程涉及的评价指标很多，但各指标间并不是互相独立的，它们之间相互关联、相互影响，存在关系不明确的问题，本质上是一种灰色关系[19]。因此，本文将灰色关联理论应用到中标单位的选择中，将选择承包商的过程看作一个涉及评价指标很多、评标过程复杂且各指标之间的关系存在不明确的灰色系统，对所有投标方案的信息进行量化处理，得到各个指标的灰色关联系数，并与组合权重复合得到各单位的灰色综合关联度，利用定量的数值来评判各个投标方案的优劣，提高评标结果的准确性和可靠性。具体计算步骤如下。

1.2.1 确定指标的初始决策矩阵

设某房屋住宅项目招标，经过资格审查后，有m家单位的投标方案进入最后评标阶段，招标单位考虑了n项指标(包含定性指标和定量指标)组成评标体系，得到第i家单位的灰色特征指标数列为

Xi=[xi(1)+xi(2)+…+xi(n)]

i=1,2,…,m

式中，xi(k)为第i个样本的第k项指标值，则m家单位和n项评标指标将构成一个mn阶的初始决策矩阵Xijm×n，其中Xij表示第i家投标单位的第j项指标得分。初始决策矩阵为

1.2.2 确定相对理想方案

相对理想方案指的是在客观上可能出现的最优秀的投标方案[20]。设相对理想方案的数据序列为X0=(x01,x02,…,xon)，将X0作为参考序列，其指标因素为x0j，其中j=1,2,…,n，代表从m个投标方案中选出的每项指标的最优值。在评价因素中，有的属于取值越小越好的成本型指标，如投标报价、工期，而像质量、施工组织设计等6项指标则属于取值越大越好的效益型指标[16]。所以有

X0j=min(x0j,x1j,…,xnj) (成本型指标)

X0j=max(x0j,x1j,…,xnj) (效益型指标)

可得最佳指标集X0与初始决策矩阵X构成的(m+1)n阶指标特征量矩阵H

(1)

1.2.3 指标规范化处理

由于评价指标之间具有不同的量纲和单位，不能进行直接比较。为了消除他们对中标单位选择的影响，保证结果的可靠性，需要对矩阵H进行无量纲化处理，转化为规范化的矩阵Y[21]。

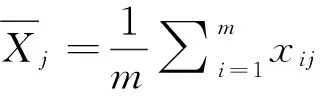
1.2.4 计算关联系数

根据灰色关联分析方法，设第i家单位的第j个评价指标在标准化的矩阵Y中的值与理想方案Y0相应指标的最佳值的关联系数为rij

1.3 层次分析法与熵权法的组合赋权

对评价指标赋权是多指标综合评价中常用的量化方法，指标权重的精确性将会影响整个评标结果的准确性。关于指标权重的计算方法一般分为两种：一种为主观赋权法，如层次分析法，德尔菲法等；另一种为客观赋权法，如离差最大化法，熵权法等，两种方法均有一定的片面性。很多学者在基于灰色关联理论对指标进行赋权时，一般单独使用主观赋权法，或者单独使用客观赋权法，只有少数学者[22]将两种方法有机地结合起来使用。但是，在对评价指标赋权时，除了要注重基于评审专家经验估计的主观权重外，还应重视反映评标指标信息量大小的客观权重[23]，使对指标的赋权同时兼顾到主客观因素，从而使评标结果更具合理性和科学性。

鉴于此，本文给出了一种组合赋权方法，利用层次分析法确定主观权重αj，熵权法确定客观权重βj，再将两者的权重通过线性加权法进行组合，可得组合赋权权重θj=ωαj+(1-ω)βj，其中j=1,2,…,n；ω为主客观权重的偏好系数，ω∈[0，1]，在求解指标综合权重时，应以主观权重为基础，根据本文的评价指标体系，取ω=0.6[18]。

1.3.1 基于AHP法的主观权重确定

(1)构建层次模型结构。根据表1，将评标过程划分为三个层次，层次模型结构见图1。

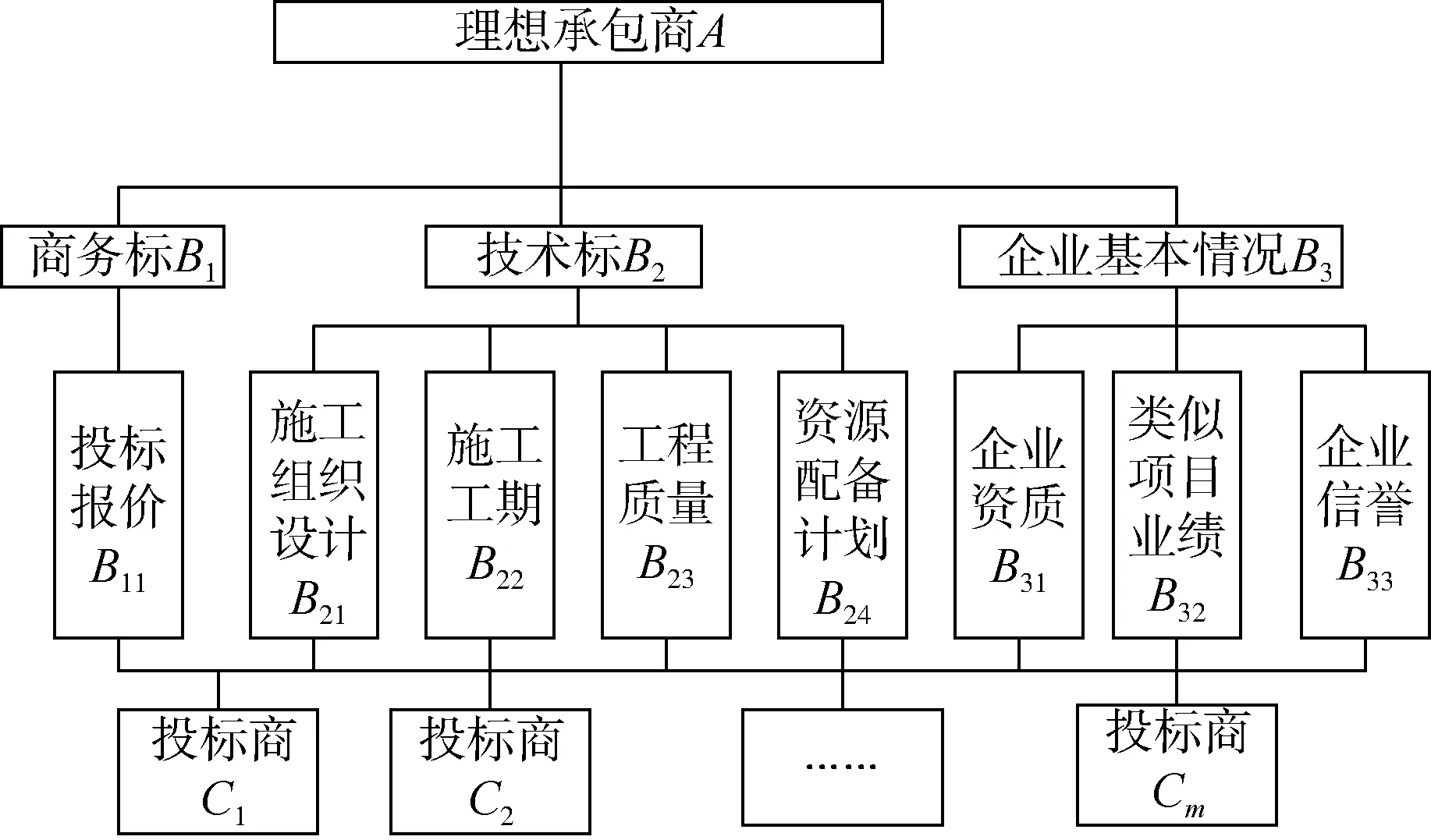
图1 建筑工程项目评标指标

(2)构造判断矩阵来判断和量化同一层次的各个指标对于上一层指标影响程度的大小，具体做法如下：

1)对于同一层的指标，每次取两个元素，通过两两比较其对上一层指标的影响程度并进行评分，全部比较的结果构成判断矩阵，见表2。

表2 判断矩阵

2)评分采用1～9比例标度法，分数越高，代表其越重要。1，3，5，7，9分别表示两个元素相比，具有相同的重要性，前者比后者稍重要，比较重要，非常重要，极端重要；2,4,6,8表示上述相邻判断的中间值。

(3)层次单排序。采用方根法求解层次单排序，计算步骤如下：

1)计算矩阵A中的每行因子之积Mi

(3)

2)对Mi进行n次开方根求

(4)

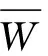
(5)

得判断矩阵A的特征向量

W=(w1，w2，…，wn)T

4)求矩阵A的主特征值

(6)

(4)检验一致性。为检验矩阵A的特征向量合理性，应对层次单排序进行一致性检验，步骤如下：

1)计算一致性指标CI

(7)

式中，n为比较因素的数量。

2)计算平均随机一致性指标RI。

根据文献[24]可得1～5阶的RI值，见表3。

表3 1～5阶平均随机一致性指标

3)计算一致性比率CR

若CR<0.1，表明判断矩阵A具有满意一致性；反之，则需重新设置判断矩阵。

(5)层次总排序。层次总排序就是利用某一层次中所有层次单排序的计算结果，综合计算出本层次所有指标相对于总目标权重的优化次序[25]。最后得到所有评价指标的权重αj，可得主观权重向量α=(α1,α2，…，αn)T。

1.3.2 基于熵权法的客观权重确定

熵用来衡量系统的无序程度，如果评价指标的熵权值越小，说明该指标包含的信息量越大，表明其在评价体系中所起的作用应该越大，赋予的权重理应越高。熵代表的是客观的结果，主要由客观的数据决定，无主观因素影响，保证评价结果的客观公正性[10]。熵权法的计算步骤如下：

(1)对指标进行规范化处理得到矩阵Z

当为效益型指标时，得

(8)

当为成本型指标时，得

(9)

(2)求出第j个评价指标的指标差异度Gj

(10)

(3)计算指标熵权βj

(11)

由此可得指标的客观权重向量

β=(β1,β2,…,βn)T

1.3.3 组合权重计算

由主观权重向量α=(α1,α2,…αn)T与客观权重向量β=(β1,β2,…βn)T可得综合集成的权重向量θ

θj=ωαj+(1-ω)βj

(12)

由此可求得组合权重向量θ=(θ1,θ2,…,θn)T，其中ω=0.6。

1.4 计算灰色综合关联度与投标单位选择

由灰色关联系数rij与指标组合权重向量θj可得各投标单位的灰色综合关联度Di

(θ1,θ2,…,θn)T

=(d1,d2,…,dm)(i=1，2，…，m)

(13)

其中，di为第i家单位的灰色综合关联度，di越大，说明该单位的灰色综合评价值越高，表明其综合实力越强，与相对理想方案的关联程度越大[26]，由此可得各方案的灰色综合关联度及优劣排序，综合关联度最高的将成为理想承包商。

2 案例分析

2.1 工程概况

南京万科置业有限公司对其G83地块项目一期进行总包招标，经过批准立项后，采用公开招标的方式招标，最后有4家投标企业通过资格审查后入围，4家单位分别记作C1，C2，C3，C4。现在南京万科要从这4家单位中选取一个最佳的中标单位，评标体系由图1中的8项指标组成。并邀请了8位专家组成评标委员会参与评标，所有选定的专家主要来自大学、房地产开发企业和政府，同时对建筑工程项目的评标制度非常熟悉。各投标单位评分情况见表4。

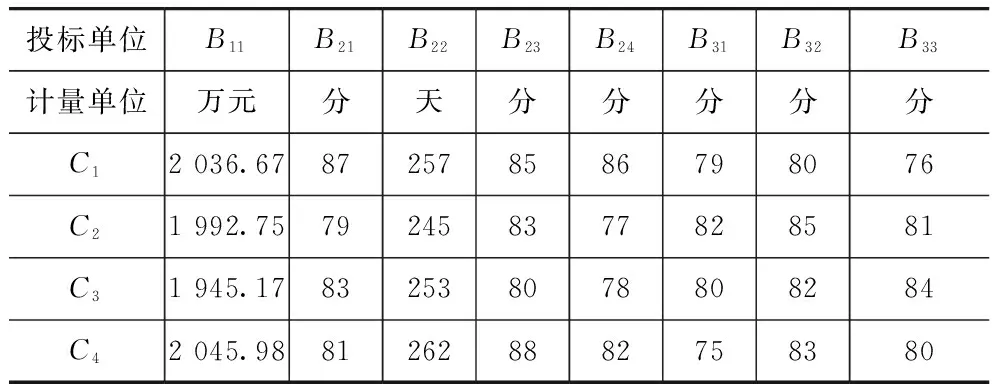
表4 投标单位评分情况

2.2 灰色关联系数的分析

2.2.1 确定相对理想方案指标集

根据表4和式(1)可得到相对理想方案的指标集X0。即

X0=(1 945.17，87，245，88，86，82，85，84)

X0与初始决策矩阵X组成指标特征向量矩阵H=(hij)5×8。即

2.2.2 指标规范化处理

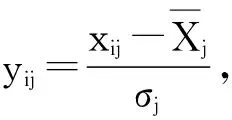
2.2.3 计算关联系数

由式(2)可求出矩阵Y中的指标值与理想方案Y0相应指标的关联系数为rij。即

2.3 确定组合权重

2.3.1 层次分析法确定主观权重

根据图1的所有评价指标，利用1～9比例标度法，两两比较可分别构造A-Bi,B2-B2i，B3-B3i，判断矩阵，再根据式(3)～式(7)求取判断矩阵的特征向量和最大特征根λmax，并进行一致性检验。层次单排序结果见表5～表7，总排序结果见表8。

表5 判断矩阵A-Bi

表6 判断矩阵B2-B2i

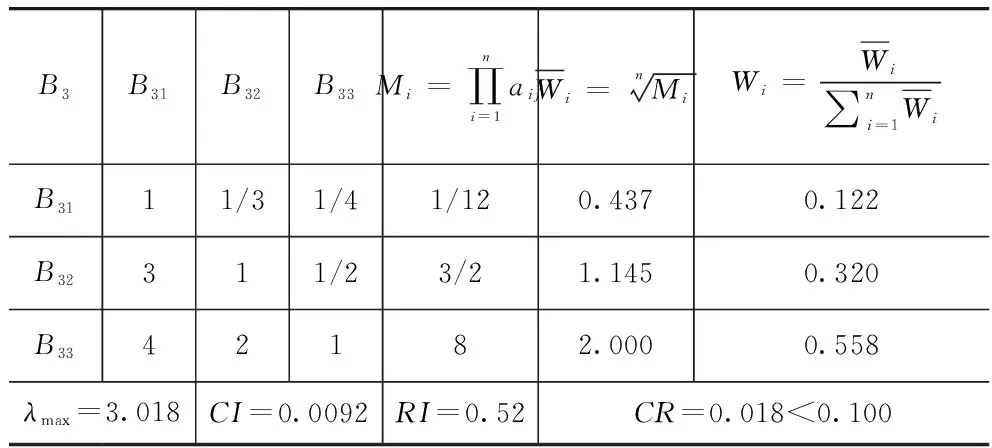
表7 判断矩阵B3-B3i

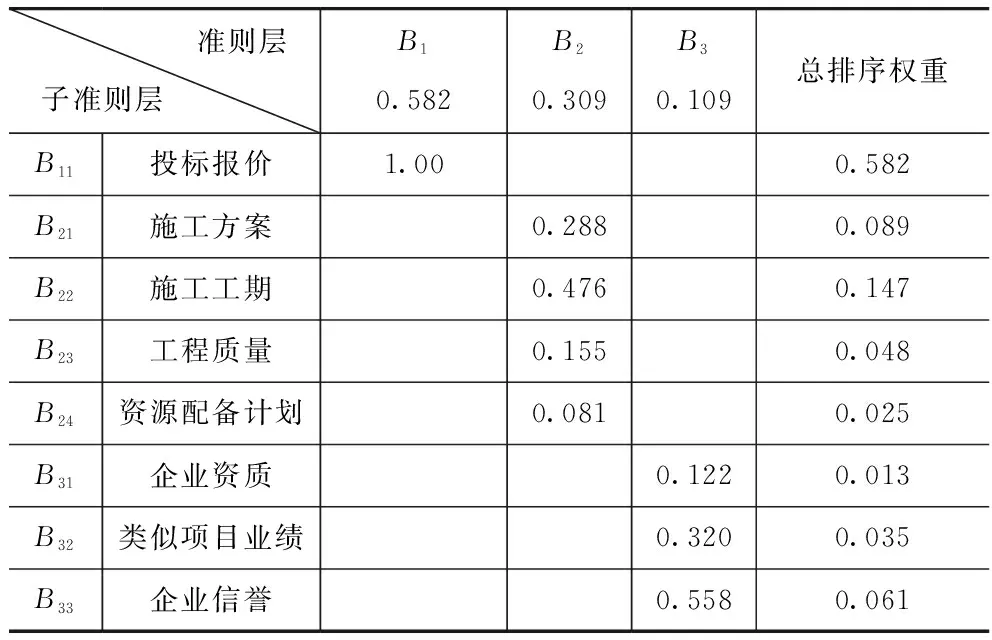
表8 评价指标总排序权重

由此可得投标单位的8个评价指标的主观权重向量为

α=(0.582，0.089，0.147，0.048，0.025，0.013，

0.035，0.061)

2.3.2 熵权法确定客观权重

根据式(8)～式(11)，可得8个评价指标客观权重的向量

β=(0.049，0.155，0.155，0.146，0.235，0.127，

0.058，0.155)T

2.3.3 确定组合权重

已知主观权重向量α与客观权重向量β，根据式(12)可求得组合权重向量

θ=(0.369，0.116，0.118，0.087，0.109，0.059，

0.044，0.09)T

2.4 确定灰色综合关联度及选择理想承包商

由式(13)，根据矩阵R和组合权重可得各单位的灰色综合关联度。

由此得到四家投标单位的灰色综合关联度比较结果为d3>d2>d1>d4，说明投标单位C3最接近理想承包商，因此选择综合评价值最高的单位C3中标。

3 结语

本文提出了一种基于灰色关联-组合赋权评标方法的模型构建方法。通过将层次分析法和熵权法线性加权来确定组合权重，不仅注重基于评审专家经验估计的主观权重，而且还重视反映评标指标信息量大小的客观权重，增加了评标的客观性与科学性。此外，通过灰色关联系数分析各指标间存在的复杂的隐性关系，并与组合权重复合得到所有投标单位的灰色综合关联度大小；据此选择理想承包商，提高了评标结果的准确性和可靠性，为评标方法向科学化与规范化发展提供了一定的参考。

[1] 卢建昌,裴乐萍.基于ISM与G-ANP的建设项目评标方法研究[J].科技研究,2014(2):31-35.

[2] 张熠,王先甲. 基于G1-法和改进DEA的工程项目评标方法[J]. 科研管理,2012(3):136-141.

[3] Yin X H, Song Y F. Research on the evaluation model of bidding risk of international engineering contractors[J]. Construction Management Modernization,2008(5):52-56.

[4] Cheng M. Evaluation model for construction projects based on AHP[J]. Journal of Huangshi Institute of Technology, 2011(2)：38-43.

[5] 杨宝臣, 陈跃. 基于组合赋权TOPSIS模型的项目评标方法研究[J]. 电子科技大学学报：社会科学版, 2011, 13(1):50-54.

[6] He X U, Shu H, Business S O, et al. Application of entropy based grey relational model in project bid evaluation[J]. Hebei Journal of Industrial Science & Technology, 2015(1)：16-20.

[7] Markabi M S，M S Sarbijan、 A hybrid model of grey relational analysis and dea cross-efficiency for the evaluation of decision making units[J]. International Journal of Economy, Management and Social Sciences，2015，4(3)：317-322.

[8] 许远明, 陶书金, 曾令德. 基于熵权-TOPSIS方法的施工评标模型应用研究[J]. 工程管理学报, 2012(5):62-65.

[9] 鲍学英,王起才. 基于信息熵和价值工程的工程评标方法研究[J]. 兰州交通大学学报,2015(4):62-65.

[10] 张攀攀.基于熵权灰色关联分析的绿色发展评价指标体系研究：以武汉市为例[J].特区经济,2015(12):90-92.

[11] 舒欢, 宁敬博. 基于组合赋权与TOPSIS法的政府工程采购评标研究[J]. 河北工业科技, 2015, 32(3):214-218.

[12] 高云莉. 基于AHP-GRAP模型的建设项目评标方法[J]. 大连民族大学学报, 2007, 9(3):54-56.

[13] 王飞, 陈鲜阁. 基于熵的灰关联模型在工程评标中的应用[J]. 河北建筑科技学院学报：自然科学版, 2013, 30(1):103-106.

[14] 陈鲜阁. EPC总承包模式下公路工程的评标模型研究[D].邯郸：河北工程大学, 2013.

[15] 曹智界.基于物元模型的建筑工程评标方法[J].低温建筑技术,2012(2):114-116.

[16] 张熠,王先甲.一种基于灰色关联和模糊理论的工程项目评标方法[J].技术经济,2009(12):43-46，57.

[17] 卢小广，刘元欣，潘海英.统计学[M].北京：机械工业出版社，2013.

[18] 刘文娜,舒欢.基于模糊物元-综合集成赋权的工程评标模型[J].土木工程与管理学报,2013(4):77-80.

[19] 黄海龙,王恩茂.基于组合权的建筑工程绿色施工水平的灰色综合评价[J].工程管理学报,2014(1):103-107.