基于子域分解的全六面体网格生成方法
2018-03-03张见明鞠传明
汪 攀 张见明 韩 磊 鞠传明
池宝涛湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
0 引言
网格生成是数值模拟的主要性能瓶颈,其自动生成算法的研究一直被广泛关注。有限元方法的成功应用在很大程度上取决于对分析对象进行有限元网格划分的合理性。相对于四面体网格,六面体网格在计算精度、划分数量、抗畸变程度以及重划分次数等方面均具有优势[1],因此六面体网格也称为黄金网格。但是,由于六面体网格复杂的拓扑关系以及较差的几何自适应能力,故针对复杂三维实体的全六面体单元网格全自动生成方法,目前仍处于探索阶段。目前有代表性的全六面体网格自动生成方法有:超限映射法[2]、扫描法[3-4]、基于栅格法[5-7]、前沿推进法[8-9]和多子区域法[10]。其中超限映射法的优点是算法简单、速度快、单元质量好、密度可控制,并且可与形状优化算法集成,因此,映射法在众多的商业有限元分析软件中占有重要的地位。但是,映射法一般只能直接处理简单的单连通域问题,并且对于带有倒圆角、小孔等小特征的三维实体,其生成的六面体网格质量不好;对于复杂的多连通域问题,通常需要首先手工将待剖分域分解成几何形状规则的可映射子区域,然后在每个子区域上应用超限映射法,这一缺陷不利于大规模全自动网格划分的实现。为了解决这一问题,PRICE等[11]提出用中面法将三维待剖分域分解成简单子区域,但是现有中面算法一般需要进行大量几何与代数计算,自动化程度和几何适应能力也有待于提高,且对于存在多凹面的几何体来说中轴面生成存在困难。
针对上述问题,本文提出了一种基于子域分解的全六面体网格自动生成方法,该方法首先提取实体模型的分解特征,然后通过分解特征形成分解面,最后利用分解面将复杂实体分解为多个可映射的简单子域,并在各子域上用超限映射法生成六面体网格。
1 算法原理
1.1 相关定义
1.1.1 与边相关的定义
(1)二面角:与边相连的两个面的夹角,设为α。
(2)凸边:当π/2-ε<α<π/2+ε时,则该边为凸边,其中ε取π/6,下同。
(3)自然边:当π-ε<α<π+ε时,则该边为自然边。
(4)凹边:当3π/2-ε<α<3π/2+ε时,则该边为凹边。
(5)反转边:当3π/2+ε<α时,则该边为反转边。
(6)特征边:凹边和反转边统称为特征边。
(7)虚边:用于形成封闭的分解环时构成出来的边。
1.1.2 与环相关的定义
(1)特征环:由相连的特征边构成的环。特征环有可能是开环,也有可能是封闭的环。
(2)分解环:由特征环和虚边组成的连续封闭的环。用于形成分割面,对三维实体进行分割。
1.1.3 与面相关的定义
分解面:由分解环得到的虚拟面,用于分割三维实体。
1.2 算法流程
本文所提出算法的主要步骤如下。
(1)识别实体的小特征,如圆倒角、同心圆、圆孔等,得到其等效的几何模型。
(2)从三维实体的等效模型中提取实体的特征边(凹边和反转边),并将其加入特征边链表。
(3)遍历特征边链表,找到相互连接的特征边,构成一个特征环,并将其加入特征环链表。注意:特征环有可能包含多连边,也有可能只有一条边,有可能是连续封闭的环,也有可能不是封闭的环。
(4)遍历特征环链表。若取到的特征环是连续封闭的环,则直接通过该特征环及其支撑面构造出分解面;若取到的特征环不是封闭的,则需要构造合适的虚边,将特征环补成连续封闭的环,然后再构造分解面。
(5)通过分解面将三维实体分割为两个部分,为了保证最终生成的体网格连续一致,需要建立这两部分实体与分解面之间的拓扑关系。
(6)对分割后的实体进行网格划分时,为了保证空间网格的一致性,要先在分解面上生成面网格,再映射到被其分割的实体表面,之后用超限映射生成六面体网格。
(7)最后将各子体的六面体网格数据合并,即得到整个三维实体的网格数据。
2 实现过程
2.1 处理小特征
2.1.1 识别小特征
对于很多机械产品,为了避免应力集中,都会引入倒圆角设计,这会导致捕获实体模型的特征边失败。如图1a所示的边a、b,其二面角α=π,此时会将a、b两条边鉴别为自然边,但是,很明显图1a所示的模型和图1b是等效的,此时体分解失败,所以需对倒圆角作特殊处理。要处理倒圆角,首先要识别倒圆角面,下面给出倒圆角面的三个条件:①面包含四条边;②有两条圆弧边、两条直线边;③两条圆弧边是对边,且其对应的圆心角相同。若给定的实体表面满足以上三个条件,则可以判定为倒圆角面。
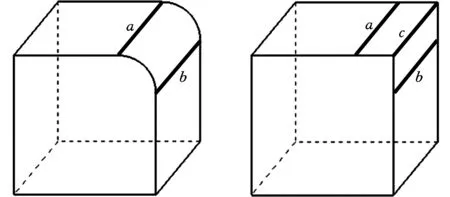
(a)原始模型 (b)等效模型 图1 倒圆角的处理Fig.1 The treatment of fillet
2.1.2 模板
机械产品中,经常会遇见带圆倒角、同心圆柱面、圆孔等小特征的实体,这些小特征的存在阻碍了六面体网格的生成,或使得生成的六面体网格质量不好,为了解决此问题,本文给出了如图2~图4所示的模板,图中所标识的点在三维空间是一条直线,引入模板以后,可以准确地识别边的类型,从而可以有效合理地进行体分解流程。其中,图2所示的模板可以准确地提取三维实体模型的特征边,从而对三维实体进行有效体分隔,图3所示的同心圆模板和图4所示的圆孔模板,可以显著地提高生成六面体网格的质量。
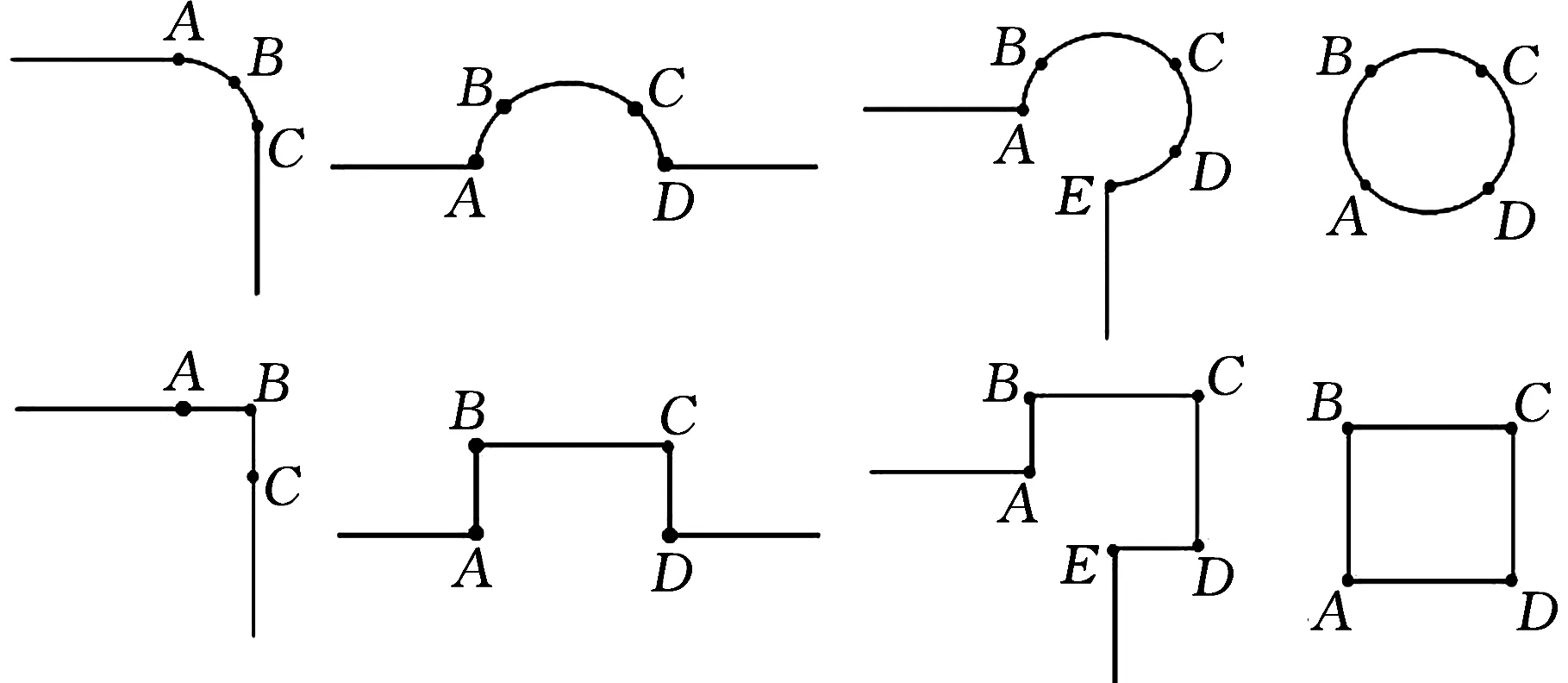
图2 倒圆角的模板Fig.2 The templates of fillet

图3 同心圆的模板Fig.3 The templates of concentric circles
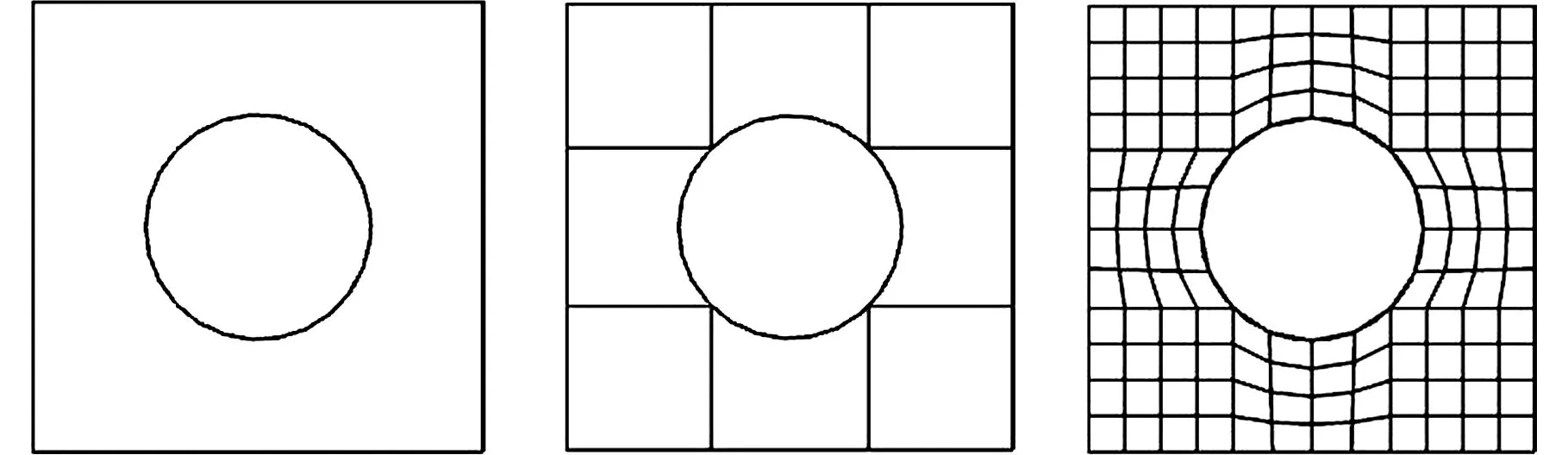
(a)几何模型 (b)分解模型 (c)网格划分图4 圆孔的模板Fig.4 The templates of hole
2.2 形成合理的分解面
2.2.1 提取特征边
特征边是三维实体上形成分解环的边,本文方法中所指的分解边是指凹边和反转边。凹边和反转边是形成分解环,最终形成分解面的基础,准确获取实体模型的分解边是进行体分解的关键步骤。获取三维实体的分解边主要包括以下两个步骤:
(1)识别三维实体的小特征,根据图2~图4所示的模板,得到其等效模型。
(2)遍历等效模型的边界边,计算其对应的二面角,并标记其类型,将凹边和反转边存在链表中,如图5所示的粗线边。
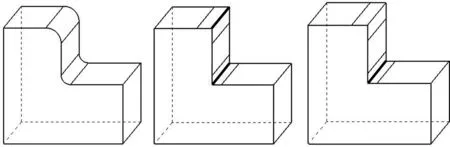
图5 圆倒角的特征边提取示意图Fig.5 The feature abstraction of fillet
2.2.2 形成分解环
获取了三维实体的特征边以后,遍历得到的特征边,相互连接的特征边组成一个分解环。当分解环是闭环时,可直接由分解环形成分解面,然后对三维实体进行有效分割;当分解环是开环时,需通过搜索形成合适的“虚拟边”,将开环补成连续封闭的分解环。封闭的分解环才能有效地对三维实体进行分割。如图6a所示的实体模型,根据上述边的定义提取到四条特征边(凹边),如图6b所示的粗线段。这4条特征边首尾相连,构成一个封闭的分解环,可直接形成分解面对三维实体进行分割。
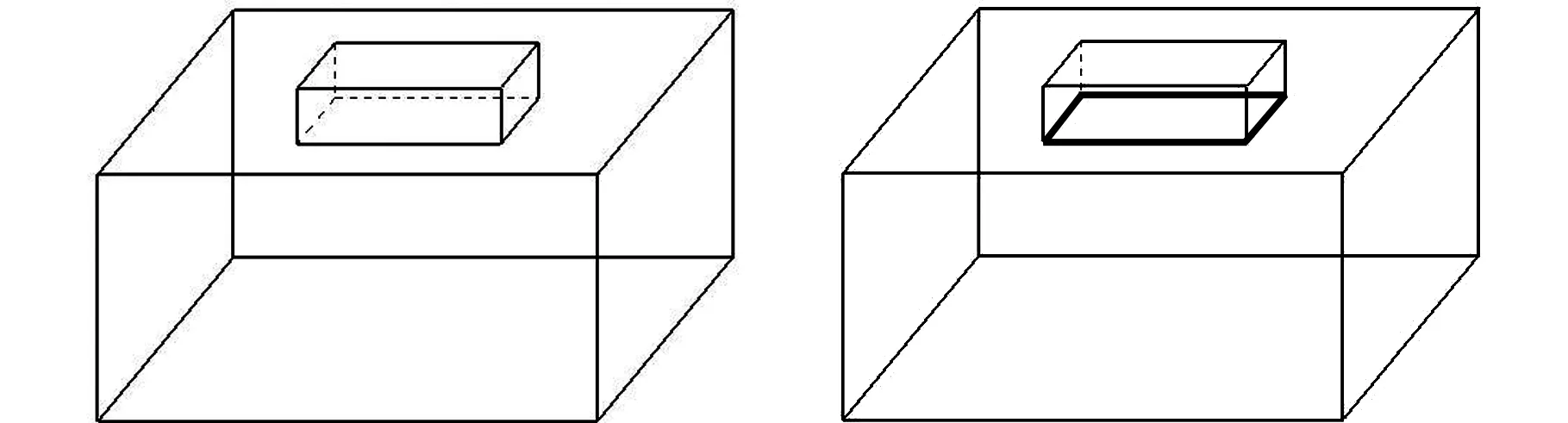
(a) (b) 图6 分解环形成示意图(一)Fig.6 The generation of parting loop
从图5所示模型的等效模型中获取的特征边如图7a所示的粗线段AB,通过该分解边形成特征环时,没有搜索到与其相连的分解边,此时该特征边形成的特征环即为一条孤立的线段,此时需要构造虚边。具体方法如下:在特征边的端点处,作与其相连的两条边的延长线,并与面上另一条边相交,该端点与交点即为一条虚边,如7b所示的粗线段AC和AD,重复上述过程,直到构建的虚边可以和分解边构成一个封闭的环。特征边沿着两个方向构造虚边,可以得到两个分解环,如图7c所示的ADEB和图7d所示的ACFB,此时需要选择一个相对合适的分解环。选取的准则如下:设分解环上最短边长度为Lmin,最长边长度为Lmax,比例β=Lmin/Lmax,取β较大的分解环,β越大,分解环的形状越趋向正方形(当分解环是四条边的时候),合理地选择分解环可以有效地避免分割后的实体出现狭长的片体,从而不利于生成高质量的六面体网格。
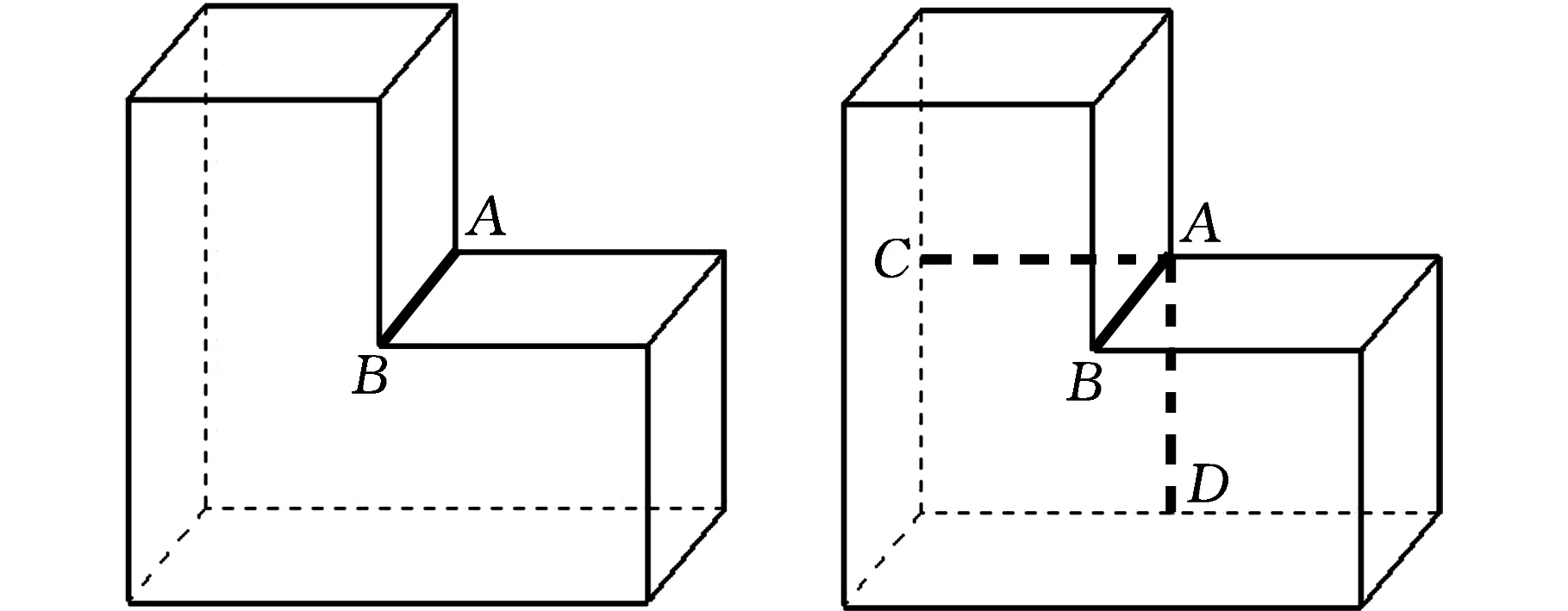
(a) (b)
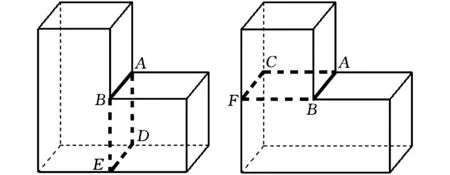
(c) (d)图7 分解环形成示意图(二)Fig.7 The generation of parting loop
2.2.3 形成分解面
三维实体之间是通过面连接的,所以需要由面来对实体进行分割。形成分解环以后,如果分解环中存在虚边,则根据分解环构建一个虚平面;如果分割环中不存在虚边,则先获取分割环在三维实体上的支撑表面(该支撑表面不一定是平面),得到支撑表面以后,根据支撑表面和分解环构造出虚面,此时的构造并不是真的生成一个面,而是在支撑面的基础上加了一个约束边界,这个虚面的几何是基于支撑面,拓扑是基于分解环。分解面形成如图8所示。

图8 分解面形成示意图Fig.8 The generation of parting plane
2.3 体分解
对于复杂实体,可能会形成多个分解面,如何利用这些分解面对三维实体进行全自动分割是本文算法的关键。为了简化程序实现过程,本文将所有分解面存储在链表中,然后遍历该链表。对于某一分解面,将目标域分解为两个子域,若这两个子域中,至少有一个可以利用超限映射法进行六面体网格划分(子域包含6个实体面或为图3、图4所示的模板),则该分解过程合法,即可以利用该分解面对目标域进行分解,否则将该分解过程延后至下一次循环。上述操作可以形象地描述为,从复杂的目标域上,逐步分割出一个可用映射法进行网格划分的子域。利用上述方法进行有序的分解,可以避免递归算法,从而节省了内存开销,且方便程序的调试与维护。分解面将目标域分解为两个子域以后,需要建立两个子域与分解面的拓扑关系。目前,大多数CAD软件采用基于边界表征[12]的数据结构(B-rep)。在边界表征的数据结构中,实体(body)是由面(face)表示的,面(face)是由环(loop)表示的,环(loop)是由边(edge)表示的。本文依据边界表征的数据结构构造分解面与两个子域的拓扑关系,首先由分解边构造分解面,然后将分解面存储于子域中用于存储几何面数组FaceArray。
2.4 子域网格划分
2.4.1 子域边界离散
用超限映射法生成六面体时,要求三维实体的几何边界离散线段数相等,因此对于每个分割后的块体,在每个面上其对应的离散线段数要相等。这实际上就是一个带约束的线性规划问题,通过求解下列方程,即可得到所有边界的离散线段数。
目标函数为
约束条件为
式中,k为进行体分解以后,三维实体包含的边;Li为第i条边的实际长度;Ls为自适应的网格尺寸值;iFX+为面上方向与X轴正向保持一致的所有边界的集合;iFX-为面上方向与X轴负向保持一致的所有边界的集合;iFY+为方向与Y轴正向保持一致的所有边界的集合;iFY-为方向与Y轴负向保持一致的所有边界的集合。
上述问题可以采用整数规划方法来求解[13]。
2.4.2 超限映射法
对三维实体进行分割以后得到的可映射子体,可以用超限映射法[13]生成六面体网格。对于任意的包含6个实体表面,且是单连通域的三维实体,其对应的参数空间为[0,1]×[0,1]×[0,1],设(ξ,η,γ)为参数空间[0,1]×[0,1]×[0,1]中任意的一点,则其对应在物理空间的坐标是由(ξ,η,γ)在6个表面上对应的坐标和8个顶点决定的[14]。对于任意的包含4条边界,且是单连通域的面,其对应的参数空间为[0,1]×[0,1],设(u,v)为参数空间[0,1]×[0,1]中任意的一点,则其对应在物理空间的坐标是由(u,v)在4条边界上对应的坐标和“四边形”面的4个顶点决定的[13],现以面的超限映射法加以说明。设“四边形”面的参数域如图9a所示,则(u,v)对应的物理域坐标可由下式得到:
式中,f1、f2、f3、f4为实体表面上四条边界,如图9b所示。

(a)参数域

(b)物理域图9 “四边形”面的物理域及参数域Fig.9 The physical domain and parameter domain of four sides face
2.5 子域网格合并
在各子域上使用超限映射法进行网格划分以后,需要将子域网格合并,从而得到整个目标域的网格。本文首先对分解面进行网格划分,并将其作为包含该分解面的两个子域在该表面上的网格数据;其次,对子域上其他表面进行网格划分,并将生成的表面网格数据加入存储目标域网格数据的容器中;然后,依次在各子域上采用超限映射法生成域内的网格数据,并将生成的域内网格数据加入目标域网格数据容器中。按照上述方式得到的网格数据在分解面上是连续一致的,且界面处的网格数据只存储一遍。界面上的网格生成示意图见图10。
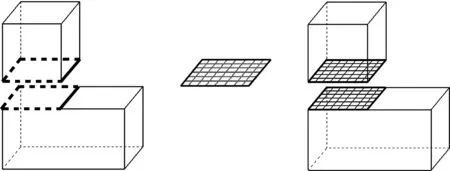
图10 界面上的面网格生成Fig.10 The mesh generation of interface
3 数值算例
下面给出三个机械零部件的六面体网格划分实例,如图11~图13所示。三个实体模型不能直接利用商业软件对其进行六面体划分,必须要进行人工分割,分解为简单子域才能有效生成六面体网格。本文利用特征识别技术可以全自动地进行体分解,得到一系列简单规则可映射的子域,然后利用超限映射法生成质量较好的结构化六面体网格,实现自动划分。
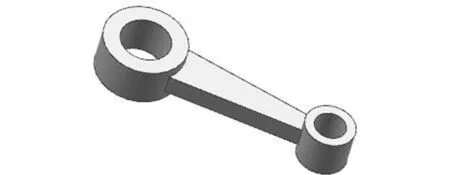
(a)原始模型
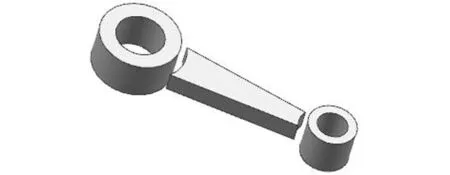
(b)分解模型
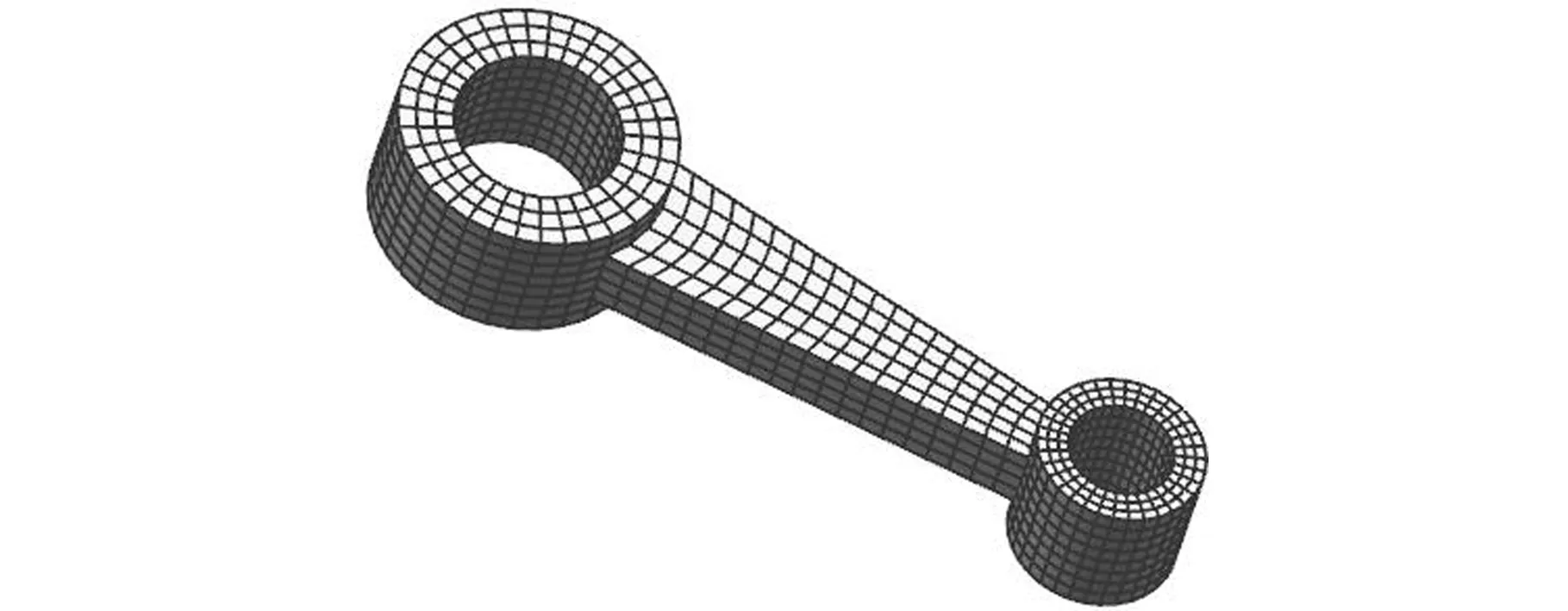
(c)生成的六面体网格图11 六面体网格生成算例一Fig.11 The first example of hexahedral mesh generation
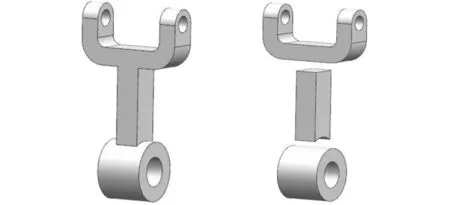
(a)原始模型 (b)分解体
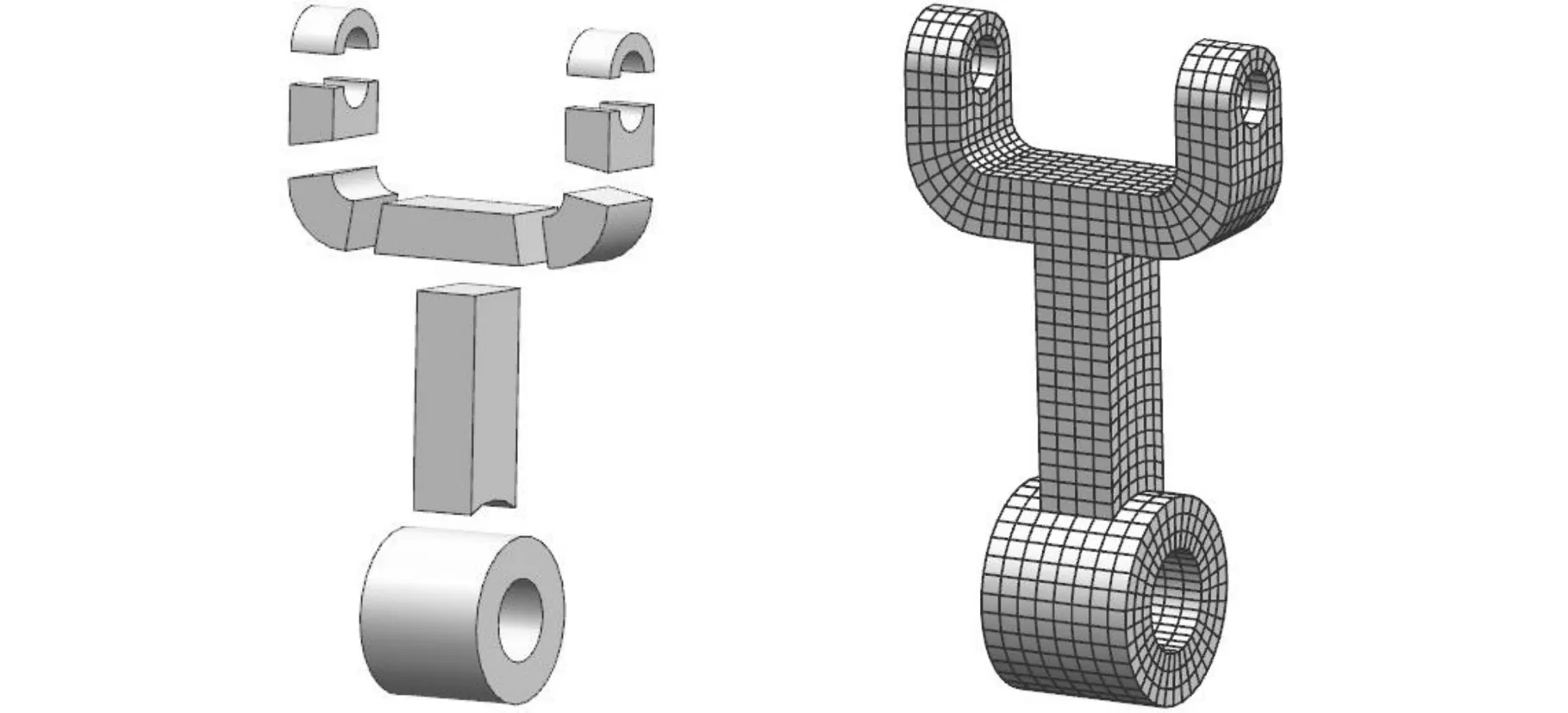
(c)进一步分解体 (d)生成的六面体网格图12 六面体网格生成算例二Fig.12 The second example of hexahedral mesh generation

图13 六面体网格生成算例三Fig.13 The third example of hexahedral mesh generation
4 总结
(1)由于子域网格是由超限映射法生成的,因此本文提出的方法能够生成质量较好的结构化六面体网格,且算法效率较高。
(2)对于含有倒角、同心圆、小孔等小特征的三维实体,本文引入的模板能够生成质量较好的六面体网格。
(3)相对于传统的商业软件,本文的算法能够全自动地生成六面体网格,避免了大量人机交互操作,提高了网格生成的效率。
(4)数值实验表明,对于无法用商业软件直接进六面体划分的复杂实体,本文提出的方法能够全自动地进行六面体网格划分。
[1] SCHONNING A, OOMMEN B, IONESCU I, et al. Hexahedral Mesh Development of Free-formed Geometry: the Human Femur Exemplified[J]. Computer-aided Design,2009,41(8):566-572.
[2] GORDON W J, THIEL L C. Transfinite Mappings and Their Application to Grid Generation[J]. Applied Mathematics & Computation,1982,10/11(4):171-233.
[3] MUKHERJEE N, PEDDI B, CABELLO J, et al. Automatic Hexahedral Sweep Mesh Generation of Open Volumes[C]//International Meshing Roundtable. Orlando,2013:333-347.
[4] 陈建军, 肖周芳, 曹建,等. 多源扫掠体全六面体网格自动生成算法[J].浙江大学学报工学版,2012,46(2):274-279. CHEN Jianjun, XIAO Fangzhou, CAO Jian, et al. Automatic Hexahedral Mesh Generation for Many-to-one Sweep Volume[J]. Journal of Zhejiang University,2012,46(2):274-279.
[5] ZHANG H, ZHAO G. Adaptive Hexahedral Mesh Generation Based on Local Domain Curvature and Thickness Using a Modified Grid-based Method[J]. Finite Elements in Analysis & Design,2007,43(9):691-704.
[6] 黄丽丽,赵国群. 基于栅格法的三维六面体网格质量优化[J]. 中国机械工程,2009,20(21):2603-2608. HUANG Lili, ZHAO Guoqun. Optimization of Grid-based Three-dimensional Hexahedral Meshes[J]. China Mechanical Engineering,2009,20(21):2603-2608.
[7] SUN L, ZHAO G. Adaptive Hexahedral Mesh Generation and Quality Optimization for Solid Models with Thin Features Using a Grid-based Method[J]. Engineering with Computers,2016,32(1):61-84.
[8] KREMER M, BOMMES D, LIM I, et al. Advanced Automatic Hexahedral Mesh Generation from Surface Quad Meshes[C]// Proceedings of International Meshing Roundtable.Orlando,2013:147-164.
[9] KAWAMURA Y, ISLAM M S, SUMI Y. A Strategy of Automatic Hexahedral Mesh Generation by Using an Improved Whisker-weaving Method with a Surface Mesh Modification Procedure[J]. Engineering with Computers,2008,24(3):215-229.
[10] TAM T K H, ARMSTRONG C G. Finite Element Meshcontrol by Integer Programming[J]. International Journal for Numerical Methods in Engineering,1993,36(15):2581-2605.
[11] PRICE M A, ARMSTRONG C G, SABIN M A. Hexahedral Mesh Generation by Medial Surface Subdivision: Part I. Solids with Convex Edges[J]. International Journal for Numerical Methods in Engineering,1995,38(19):3335-3359.
[12] 孙家广. 计算机图形学[M]. 3版.北京: 清华大学出版社, 1998. SUN Jiaguang. Computer Graphics[M]. 3rd ed. Beijing: Tsinghua University Press,1998.
[13] WHITELEY M, WHITE D, BENZLEY S, et al. Two and Three-quarter Dimensional Meshing Facilitators[J]. Engineering with Computers,1996,12(3):144-154.
[14] LI T S, ARMSTRONG C G, MCKEAG R M. Quad Mesh Generation fork-sided Faces and Hex Mesh Generation for Trivalent Polyhedral[J]. Finite Elements in Analysis & Design,1997,26(4):279-301.
