钻井工况下单金属密封接触分析及实验研究

张 毅 常学平 付玉坤 吴 倩

1.西南石油大学机电工程学院,成都,6105002.中国石油西南油气田分公司工程技术研究院,成都,610017

0 引言

单金属密封具有抗振动、耐高温高压和耐磨损的特点，被广泛应用于石油钻采领域[1]，该类密封可以有效地延长轴承的寿命，降低钻井成本。Hughes公司针对钻头工作的特殊环境，充分考虑了井底的振动、高温高压对钻头动密封的影响，开发出了具有优良性能的单金属密封，使得钻头动密封面的受力情况更加合理，牙轮钻头的寿命也得到了进一步延长[2]。

该单金属密封不仅要承受钻井过程中的冲击，而且还要承受井下接近160 ℃的高温和20 MPa左右的接触压力，工作条件较为恶劣，目前国内外学者对单金属密封的研究相对较少，且大多处于起步阶段。国外XIONG等[3-4]结合牙轮钻头的静态工况对单金属密封的接触压力和泄漏率进行了研究。国内学者的研究主要集中在单金属密封的结构优化上，罗纬等[5]对单金属密封进行了实验研究；张宝生等[6]对单金属密封进行了有限元分析，但其研究中没有考虑井下高压环境对密封的影响；孙健等[7]对单金属密封的装配和在不同环境压力下的应力变化进行了研究；张晓东等[8]结合涡轮钻具的实际工况，对单金属密封进行了结构安装设计和轴向力的理论推导。

可以看出，目前国内学者主要是对单金属密封装配过程中的接触压力进行优化，未结合实际钻井工况，且对动密封的泄漏率也没有展开相关研究。本文在高压工况下动密封面接触压力分析的基础上，采用逆解法对动密封面的油膜厚度进行近似求解，求得在最小油膜厚度处密封面间的泄漏率，并通过实验对分析结果进行了验证。

1 单金属密封有限元分析

牙轮钻头上单金属密封结构如图1所示。图中，随主轴转动的动环和静止的静环形成动密封面，橡胶支撑环和O形圈提供密封所需要的轴向力。

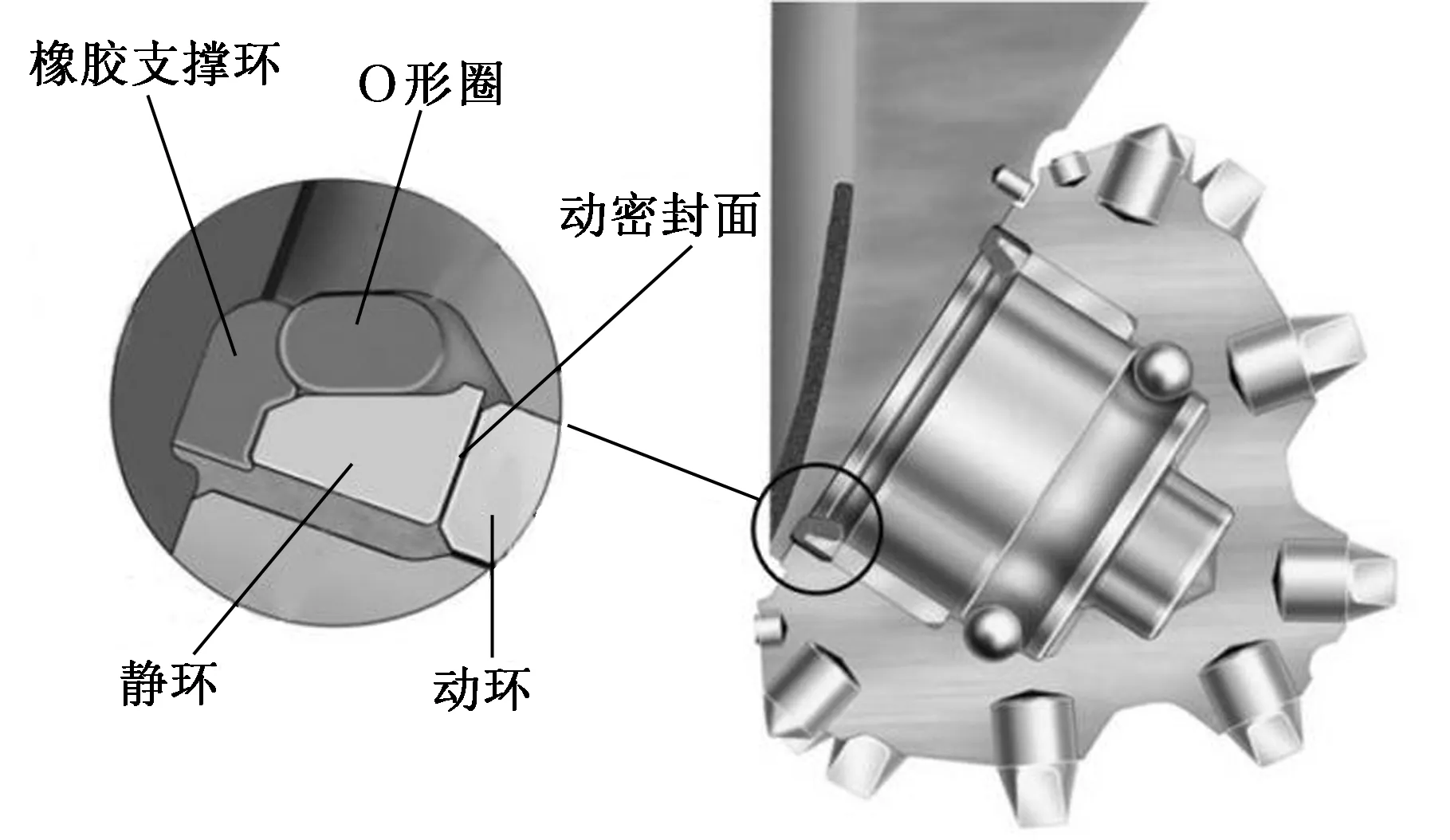
图1 单金属密封结构图Fig.1 Structure of single metal seal

井下高温高压环境对单金属密封的动密封面的接触压力有较大影响，本文仅考虑在环境压力作用下的接触面的受力情况，暂不考虑热力耦合对密封的综合效应。

1.1 有限元模型的建立

单金属密封的外侧为钻井液，内侧为润滑油，通过压力平衡系统使润滑油压力稍高于钻井液压力，从而保证钻井液不会进入密封腔内，润滑油和钻井液的压差Δp为0.3～0.7 MPa[4]，本文分析选取的压差为0.5 MPa。首先，进行单金属密封的装配过程，在装配过程分析完成后，橡胶元件会发生较大的变形，因此需要导出变形的有限元网格，然后在O形橡胶圈和静环的内表面上施加润滑油压力，在橡胶支撑环和静环的外表面上施加钻井液压力。本文根据钻井的实际工况，选取3种钻井液压力和对应的润滑油压力，同时对动环的上表面和密封座的下表面施加固定约束，润滑油压力和钻井液压力(即环境压力)载荷施加的有限单元模型如图2所示。

(a)载荷步1 (b)载荷步2 图2 环境压力下有限元加载模型Fig.2 Finite model under the environmental pressure

1.2 有限元分析结果

图3所示为单金属密封的动密封面接触压力分布情况。随着环境压力的增大，动密封面的接触压力峰值由密封的外侧逐渐向内侧转移，当钻井液压力为3 MPa时，动密封面的接触压力呈现外侧高、内侧低的状态，动密封面呈内楔形收敛，有利于润滑油膜的形成；而当钻井液压力增大到30 MPa时，动密封面的接触压力则呈现外侧低、内侧高，与钻开液压力为3 MPa的情况相反。同时在高压工况下，动密封面间不易形成润滑油膜，且外部磨砺性颗粒易于进入外侧的动密封面。

(a)p1=3 MPa (b)p1=15 MPa (c)p1=30 MPa图3 不同环境压力下动密封面接触压力分布情况Fig.3 Contact pressure under different environment pressure

2 单金属密封泄漏率计算

2.1 混合摩擦动密封计算模型

单金属密封动密封面处于流体动压润滑的情况时，动密封面间的油膜厚度分布均由Reynolds方程求出。假设动静环的轴线始终重合，同一半径r处的油膜厚度和油膜压力沿周向保持不变，不考虑温度对油膜的影响，则液膜压力计算模型可以表示为[10]

(1)

式中，h为油膜厚度；η为流体的动力黏度；p为密封面的压力分布；φγ为压力流量因子。

(2)

式中，σ为两表面综合粗糙度；γ为动静环表面微凸体的长宽之比；c为与σ和γ相关的系数。

此处c=0.9，σ=0.56，γ=0.1。

由式(1)和式(2)确定动密封面的油膜厚度和压力分布后，可计算出动密封面的泄漏率Q为

(3)

由于不考虑温度对油膜的影响，因此本文将采用逆解法，根据ANSYS有限元仿真求出动密封面的接触压力，通过MATLAB数据拟合得到密封面的压力梯度分布，再结合式(1)求得密封面的油膜分布。当接触压力梯度为最大值时，润滑油膜厚度取最小值；通过式(3)即可求得在最小油膜厚度处密封面间的泄漏率[11]。

2.2 钻井压力作用下的泄漏率

由于在高压下的动密封泄漏率的变化情况难以通过实验获得，本文将根据泄漏率的计算模型，计算钻井液压力对泄漏率的影响。忽略钻井过程中地层温度变化对润滑脂粘度的影响，假设钻井环境为θ=50 ℃，对应的润滑脂动力黏度为1.562 Pa/s，动密封的转速为n=200 r/min，润滑油和钻井液的压差为0.5 MPa。计算的泄漏率随钻井液压力的变化情况如图4所示。由图4可以看出，随着钻井液压力的增大，初期阶段的泄漏率增大较快，但在钻井液压力为10 MPa以后，动密封泄漏率增大的幅度开始降低。

图4 钻井液压力对泄漏率的影响Fig.4 Effect of drilling fluid pressure on leakage rate

3 实验研究

3.1 实验装置

图5所示为根据钻井工况搭建的双侧充压动密封实验台。密封腔体分为钻井液腔和润滑油腔，与平衡缸活塞两侧的钻井液和润滑油分别连通，通过平衡缸活塞可以保证密封两侧的压差为一稳定的压力，同时避免了高压工况对动密封面的挤压变形。扭矩传感器和位移传感器可分别测得密封的摩擦扭矩和泄漏率。实验模拟钻井液压力为3.0 MPa、1.0 MPa和0.5 MPa，对应的润滑油压力为3.5 MPa、1.5 MPa和1.0 MPa。钻井液介质为清水加适量废弃泥浆，同时由于动密封泄漏率与润滑油黏度有较大的关系，故本文选择钻头用润滑脂。实验台密封腔内的加热器可将润滑脂和模拟钻井液加热到50 ℃，从而能更好地模拟实际工况。

图5 密封实验台方案图Fig.5 Scheme of seal experimental bed

3.2 实验过程

密封工作过程中的接触面压力是不能够直接得到的，可通过测量接触面的温度来反映密封径向的受压情况，密封环背面安装的三个铠装式热电偶可测得对应位置的温度，单金属密封试件如图6所示。

图6 单金属密封试件Fig.6 Single metalseal specimen

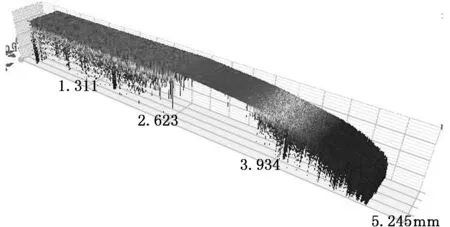
图7 动环密封面磨损深度Fig.7 Wear depth of the rotor sealing surface

有限元分析结果表明:在低压工况下密封的外侧接触压力要高于内侧，进而造成外侧磨损严重。图7所示为钻井液压力在3 MPa下的动环密封面磨损形貌。由图7可以看出，密封环的外侧磨损比较严重，表明在低压工况下密封面外侧的接触压力较大，故实验结果和仿真分析结果基本一致。

3.3 实验和仿真计算结果对比3.3.1 不同环境压力下测试温度和接触压力对比

动密封面的接触压力的仿真结果和温度测试对比如图8所示。由图8可以看出，随着密封环半径的增大，动密封面的接触压力逐渐增大，对应的测试温度也是逐渐升高。

(a)接触压力 (b)测试温度

图8 钻井液压力对接触压力和测试温度的影响
Fig.8 Effect of environmental pressure on the contact pressure and temperature

同时随着钻井液压力的增大，动密封面内侧的接触压力增幅远大于外侧的接触压力增幅，所以当实验钻井液压力增大到实际钻井的高压工况时，动密封面内侧接触压力就会大于外侧接触压力，这与测试得到的动密封面温度分布变化趋势也是一致的。

3.3.2 不同压差下测试温度和接触压力对比

在钻井过程中地层温度的升高会导致密封腔内的润滑油压力升高，密封内外的压差也会随之改变，该压差直接影响动密封面的接触压力分布情况。图9所示为不同压差作用下测试温度和接触压力的对比情况。由图9可以看出,随着压差的增大，动密封面内侧接触压力逐渐减小，外侧接触压力逐渐增大。

(a)接触压力 (b)测试温度

图9 压差对测试温度和接触压力的影响
Fig.9 Effect of environmental pressure difference on the contact pressure and temperature

3.3.3 不同转速下泄漏率计算和实验对比

图10所示为不同转速对动密封面泄漏量的影响，此时的钻井液压力为3.0 MPa。由图10可以看出，随着转速的升高，泄漏率逐渐增加，尤其在200～400 r/min之间，泄漏率增大的幅度比较大。实际钻井过程中，为了延长密封的寿命，应尽可能避开这一转速区间。

图10 转速对泄漏率的影响Fig.10 Effect of the speed on leakage rate

3.3.4 不同轴向位移下泄漏率计算和实验对比

单金属密封装配过程中，动环的轴向位移直接影响到橡胶的变形情况，进而导致动密封面上的接触压力梯度分布有较大的变化。图11所示为不同轴向位移影响下泄漏率的数值计算和实验对比情况。由图11可以看出，随着动环轴向位移的增大，动密封泄漏率逐渐降低，当动环轴向位移达到3.5 mm且继续增大时，泄漏率的降低趋势逐渐缓慢。

图11 轴向位移对泄漏率的影响Fig.11 Effect of the compressive displacement on leakage rate

由于数值计算未考虑温度对密封面受力的耦合作用，同时动密封运转过程中振动也会增加动密封的泄漏量，因此数值计算和实验结果有一定的偏差，但变化趋势基本一致。

4 结论

(1)对高压钻井液和润滑油综合作用下的单金属动密封进行有限元分析，动密封面处的接触压力最大值处于静环内侧附近，且应力分布呈发散状态，不利于形成润滑油膜。

(2)依据有限元仿真分析结果，结合MATLAB求得在最小油膜厚度处密封面间的泄漏率，提出一种计算动密封泄漏率的新方法。

(3)随着润滑油和钻井液压差的增大，动密封面内侧的接触压力逐渐减小，而外侧逐渐增大。

(4)泄漏率随着密封转速的升高而增加，初始阶段，泄漏率增加较快，当转速超过400 r/min时，泄漏率增大的幅度开始减小，实际应用中应避开200～400 r/min这一转速范围。

(5)随着动密封轴向位移的增加，泄漏率逐渐降低，当轴向位移超过3.5mm时，泄漏率降低的幅度开始减小。

[1] 张宝生，陈家庆.单金属浮动密封技术研究[J].润滑与密封，2008，33(3)：99-102. ZHANG Baosheng, CHEN Jiaqing. Research on the Technology of Single Metal Floating Seal[J]. Lubrication Engineering, 2008,33(3):99-102.

[2] Al-WAHEDI T, HAY M, WAHEED T, et al. New Slim Hole Technology Maximizes Productivity in Middle East Horizontal Drilling Programs[C]// SPE Drilling Conference. Amsterdam, Netherlands,2005,23-25.

[3] XIONG Shunhe, SALANT R F. A Dynamic Model of a Contacting Mechanical Seal for Down-Hole Tools[J]. Journal of Tribology,2003,125:391-402.

[4] XIONG Shunhe, SALANT R F. A Numerical Model of a Rock Bit Bearing Seal[J]. Tribology Transactions, 2000,43(3):542-548.

[5] 罗纬，何其翔，刘剑. 牙轮钻头金属浮动密封研究及设计[J]. 石油机械，1994, 22(12):16-19. LUO Wei, HE Qixiang, LIU Jian. Research on Metal Floating Seal for Roller Bits[J].Petroleum Machinery, 1994, 22(12):16-19.

[6] 张宝生，陈家庆，蒋立培.牙轮钻头单金属浮动密封结构的密封机理[J]. 石油机械,2003,31(3):1-3. ZHANG Baosheng, CHEN Jiaqing, JIANG Lipei. Floating Single Sealing Mechanism of the Metallic Sealing Structure of Rotary Drill Bit[J]. Petroleum Machinery,2003,31(3):1-3.

[7] 孙健， 迟可伟, 冯茂林，等. 浮动端面结构的性能分析[J]. 石油矿场机械，2006,35(1):14-18. SUN Jian. CHI Kewei, FENG Maolin, et al. Performance Analysis of Floating end Face Structure[J]. Oil Field Equipment,2006,35(1):14-18.

[8] 张晓东，张毅，李一岚，等. 单金属密封总装设计和润滑理论分析[J]. 机械设计与研究，2013,29(6):132-137. ZHANG Xiaodong, ZHANG Yi, LI Yilan, et al. Container Design and Contact Research of Single Metal Seal[J]. Machine Design and Research,2013,29(6):132-137.

[9] 刘健，仇性启，薄万顺，等. 橡胶O形密封圈最大接触压力数值分析[J]. 润滑与密封,2010,35(1):41-44. LIU Jian, QIU Xingqi, BO Wanshun, et al. Numerical Analysis of Maximum Contact Pressure of Rubber O-shaped Sealing Ring[J]. Lubrication Engineering,2010,35(1):41-44.

[10] 温诗铸，杨沛然. 弹性流体动力润滑[M]. 北京：清华大学出版社,1992:54-60. WEN Shizhu, YANG Peiran. Elastic Hydrodynamic Lubrication[M]. Beijing: Tsinghua University Press,1992:54-60.

[11] 崔晓，董彦良，赵克定. 基于ADINA的组合式动密封泄漏率与摩擦力计算[J]. 华南理工大学学报(自然科学版),2010，38(2)：95-100. CUI Xiao, DONG Yanliang, ZHAO Keding. Calculation of Leakage and Friction of Combined Dynamic Seal Based on ADINA [J]. Journal of South China University of Technology(Natural Science Edition),2010,38(2):95-100.