一种适用于MIMO多路中继信道的Lattice编码方案
2018-03-02魏天伟
赵 翔,魏天伟
(1.中国科学院上海微系统与信息技术研究所,上海 200050;2.中国科学院大学,北京100049; 3.上海科技大学,上海 201210)
0 概述
物理层网络编码(Physical-layer Network Coding,PNC)在过去数十年里取得了非常大的成功[1]。 在文献[2]中,PNC和嵌套Lattice编码在双向中继信道(Two Way Relay Channel,TWRC)中的应用使得系统可达速率已经到了距离信道容量只差1/2 bit。之后,多输入多输出(Multiple-Input Multiple-Output,MIMO)系统在TWRC中的引入又进一步增加了系统的性能。文献[3-6]描述了一些非常有效的编码方案,如线性预编码、嵌套Lattice编码、串行干扰消除等。这些技术运用又使得通信系统的性能得到了很大的提高。
近年来,对多路中继信道(Multi-way Relay Channel,MRC)的研究也越来越多。在多路中继信道中,各个用户通过中继的帮助来互相共享信息[7-9]。特别地,文献[8-9]的模型假设各个用户都工作在互相配对的模式下。最近,文献[10-11]的工作又设想了一种叫做全速率交换的系统模式,在这个模型中,每个用户都需要知道所有其他用户的信息。其实这个系统模型在很多场合都是适用的。比如自组织网络,假设在这个网络里面所有的节点都需要和其他节点共享某一个文件,但是每个节点都只拥有这份文件的某一些不同的部分,这就是一个典型的全速率交换模型。文献[10-12]也对MIMO多路中继模型的自由度(Degree of Freedom,DoF)进行了分析。然而,实现系统最优的自由度未必可以实现最好的系统性能和系统信道容量。文献[3]提出的基于Lattice编码和广义奇异值分解(Generalized Singular Value Decomposition,GSVD)的方法在用户数是2的时候(即系统模型退化成双向中继信道)能够实现较好的性能,但是该方案对于用户数大于等于3的情况下就不适用了。因此,在现有的技术基础上,提出一种可以在有限信噪比下更加高效的逼近系统信道容量的普遍适用方案就变得很有意义。
本文针对全速率交换模型,提出一种新的编码方案。为了达到最佳的系统性能,此方案结合了上述的Lattice编码以及MIMO技术,并且也运用到了线性预编码等传统操作。
1 理论基础
1.1 系统模型
如图1所示,考虑一种MIMO MRC模型,中继有N天线,每个用户有M天线,每个用户之间无法直接通信,各用户必须通过中继的帮助来获取其他K-1个用户的信息。假设信道是实信道,并且系统工作在全双工的情况下。本文的方法可以直接拓展到半双工的情况下。
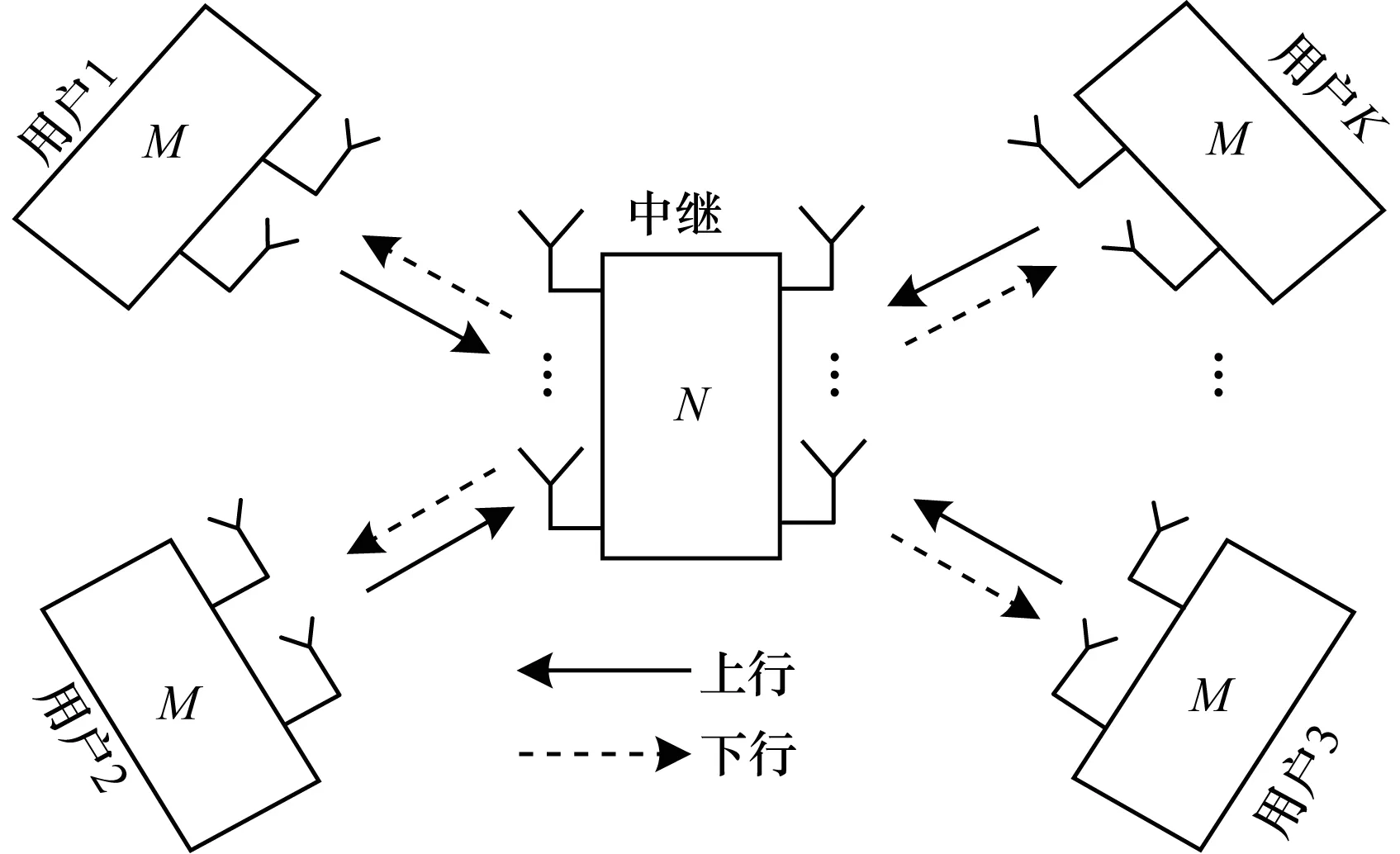
图1 K用户的多路中继信道模型
每一轮信道传递都是经过2个过程,上行过程和下行过程。在上行中,所有K个用户同时向中继发送信息,中继的接收信道如下:
(1)

(2)
其中,Pk表示用户k的功率限制。
在下行中,中继将所有的K个用户的信息同时广播出去,每个用户收到的信息为:
Yk=HRkXR+Zk,k=1,2,…,K
(3)

(4)
其中,PR表示中继的发送功率限制。
在以上讨论中,假设信道矩阵在整个过程中保持不变,并且矩阵中的各个元素服从某个独立的分布。因此,这里的信道矩阵以接近1的概率趋近于满秩。另外,假设信道矩阵在整个通信过程都是已知的。
1.2 可达速率
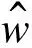
1.3 理论容量上界
现在根据已知结论描述基于MIMO的多路中继下的容量上界。设用户k的协方差矩阵为Qkk∈{1,2,…,K},那么从文献[13]中的cut-set定理可知,MIMO多路中继系统的最终可达速率空间可以描述为:
(5)

(6)
当用户个数k=1时,cut-set定理里面的2个Cut如图2所示。因此,本文中所提的MIMO多路中继模型的可达速率空间就由式(5)和式(6)所描述的所有的可达速率的闭集合所构成。
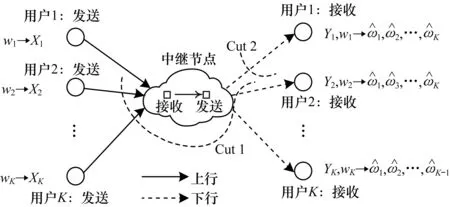
图2 当k=1时的多路中继信道的等效模型
这个最优的可达速率空间可以通过优化用户k的协方差矩阵Qk和中继的协方差矩阵QR来实现。注意到log-det函数是一个凸函数,因此,整个问题是一个凸问题,可以用标准的凸优化工具来解决。
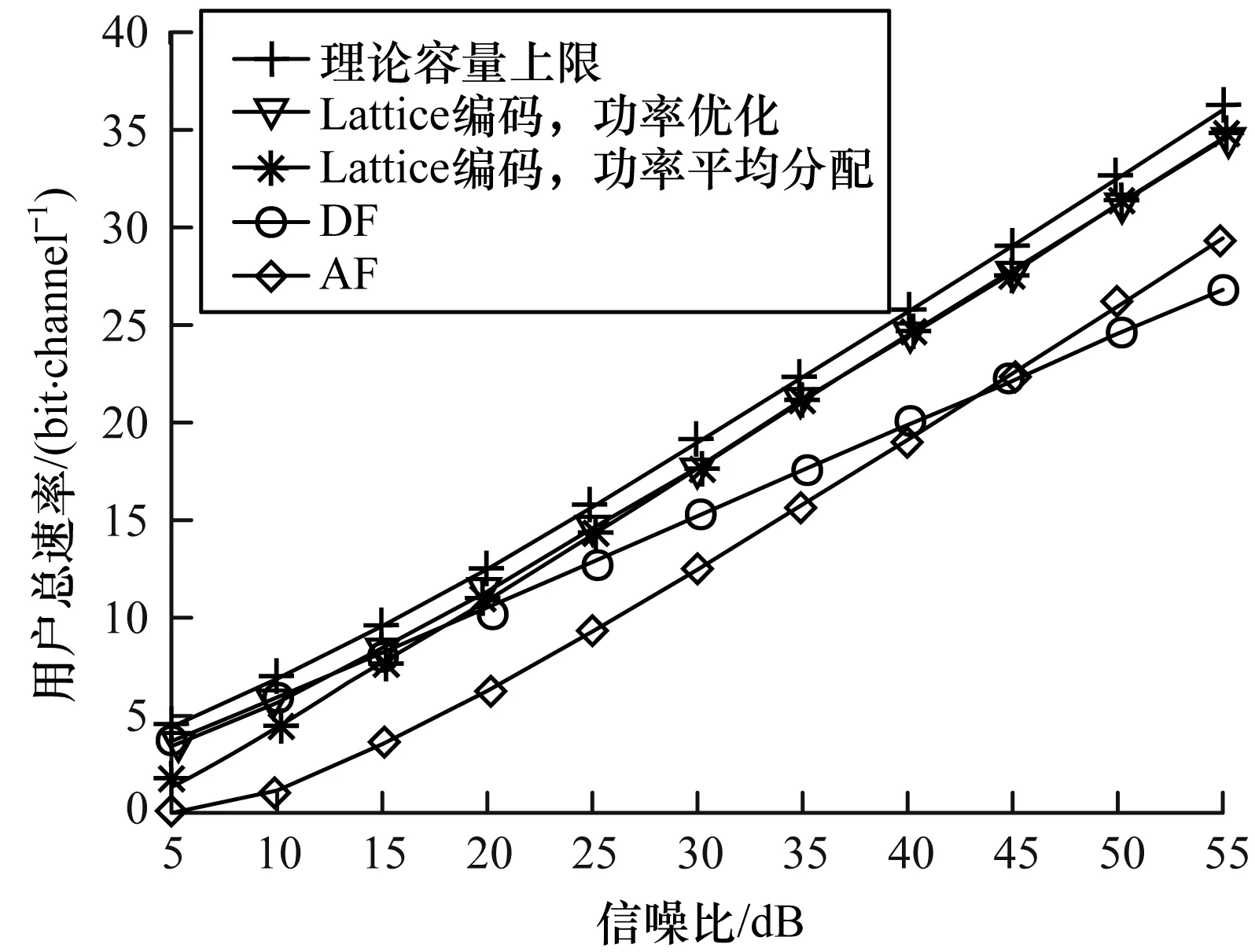
2 基于Lattice的编码实现与应用
在这个部分中,主要考虑的情况是M≥N情况下的多路中继信道。在本文结尾将简要地介绍一下M URHkR=RkRUkR (7) (8) (9) (10) 用户k的发送功率限制为: (11) 上述所有的操作均是线性的,并且完全没有信息损失的。因此,可以专注于考虑式(3)和式(7)的中继端收发方案的设计。 (12) (13) (14) (15) 上述的第n个子信道接收到的信息向量可以写作: (16) 需要注意的是在每一个时隙l中,只有用户l和用户l+1共2个用户处于激活状态传送信息。假设用户k在第n个子信道所能在空间空发送的消息集合是Wk,n={1,2,…,2TRk,n},此集合中的元素ωk,n∈Wk,n就是实际发送的信息,其中,Rk,n是用户在k第n个子信道发送的信息率。集合{ω1,n,ω2,n,…,ωK,n}就是第n个子信道的数据包。 其中,Vol(Λ)和LatticeΛ的Voronoi 区域的体积,Pk,n是用户k在第n个子信道上所发送信息的平均功率。当T→∞时o(1)→0。因此,Rk,n和Rk′,n的关系可以表述为: (17) (18) 用户在任一子信道的发送策略示意图如图3所示。 图3 用户上行发送策略 (19) (20) dk,n)modΛk,n=ck,nmodΛk,n=ck,n,fork=l,l+1 (21) (22) (23) ck′+1,n,fork′=k,k+1,…,K-1 定理1当T→+∞,对于本文所考虑的多路中继系统模型。如果下式成立,那么这样一组可达速率空间(R1,R2,…,RK)就是可以实现的: (24) (25) 其中,{Pk,n} 满足以下功率限制: (26) (27) 注释1本文假设M≥N。文中所提出的方案也可以利用禁用N-M个天线的方式直接的推广到M 现在分析在高信噪比情况下所提的方案和理论容量上界的差距。首先考虑K=2的情况(即双向中继信道),定义SNR=1/σ2。则有如下的结论: 定理2对于MIMO多路中继信道,当K=2时,本文所提的嵌套Lattice编码方案在高信噪比下可以近似地达到信道容量上界。 证明:从式(6)和式(25)可以看出本文方案在只考虑下行链路时可以达到信道容量上界的。因此,只需考虑上行的情况下是否可以达到信道容量上界。从式(5)可以得到: (28) (29) 另一方面,在高信噪比时,本文所提方案的功率近似平均分配的,因此,上行部分式(25)有如下表达方式: (30) 因此,可以看出,本文所提出的嵌套Lattice方案在高信噪比下可以达到信道容量上界。证明完毕。 注释2至此文截稿日止,只有文献[3]所提出的GSVD的Nested-lattice编码方案可以在高信噪比下近似地达到容量上界。本文提出了另外一种基于Lattice的编码方案可以达到容量上界。这2种方案的主要差别在于本文的方案是利用Lattice编码在用户端预先消除了码流间干扰,但是文献[3]是利用GSVD的方法在中继节点消除了码流间干扰。 证明:根据式(24),在高信噪比下: (31) (32) (33) 其中,式(32)是利用log-det函数的凹性以及詹森不等式得出的结果。将式(33)和式(5)对比即完成定理3的证明。 从定理3可以看出,本文所提出的嵌套Lattice 的编码方案在高信噪比情况下并不确切逼近容量极限,但是这并不表明本文所提的方案并不是最优的。因为这个差距随着SNR的增加并不能看出是否在减小。 在这一部分中,本文所提出的方案将被整理成优化问题,从而得到其最优速率,然后将其和传统的其他方案进行对比。 本文方案的优化问题可写成如下形式: subject to trQR≤PR,QR0 (34) 上述问题可以通过标准的CVX优化工具来解决。由于篇幅限制,这里忽略优化细节。 作为对比,解码转发(Decode and Forward,DF)和放大转发(Amplify and Forward,AF)方案也被列出。在DF中,需要中继完全解码从K个用户发送过来的信号。此时可达速率空间就是一个K用户的多址接入信道。DF中下行链路和本文所提的方案是一致的,都是广播过程,可达速率限制也和式(23)一致。因此,DF的可达速率的优化问题可以如下表达: subject to trQR≤PR,QR0 trQk≤Pk,Qk0,for∀k (35) 其中,集合SK{1,2,…,K}。 在AF模式中,中继将接收到的信号向量乘以一个放大系数,这个放大系数取决于中继的功率限制。其可达速率空间表达式由式(37)给出: ∀k′∈SK,S⊆SKk′ (36) subject to (36),trQk≤Pk,Qk0,∀k,α>0 (37) 上述AF和DF优化问题同样可以用标准的凸优化工具解决,这里忽略优化细节。 图4 各种方案性能对比 从图4中可以看出,本文的方案在高信噪比下,最优功率分配方案和平均功率分配方案基本一致的,这也大大地简化了计算复杂度。从图中也可以看出,本文所提的方案和容量上界的斜率是一致的。这就说明本文的方案实现了最大的分集增益。此外,从图中可以看出本文的方案在信噪比为40 dB的时候距离容量上界大约是1 bit/channel的差距。这也和定理3相吻合。从图4可以看出,本文的方案要比DF方案好5 bit/channel,并且这个差距随着SNR的增长还是逐渐增长的。图中也表明本文的方案在任何时候都要比AF的方案表现更好。原因是AF方案中将很大一部分功率浪费在了对噪声的放大作用上面。 本文提出一种适用于MIMO多路中继信道的基于嵌套Lattice的编码方案,并推导出了这种编码方案的可达速率。仿真结果表明,与传统的解码转发模式和放大转发模式相比,本文所提的方案有比较大的性能优势,在用户数K=2时,可以达到信道容量上界。 [1] ZHANG Shengli,LIEW S C,LAM P P.Hot Topic:Physical-layer Network Coding[C]//Proceedings of ACM MobiCom’06.Los Angeles,USA:[s.n.],2006:358-365. [2] NAM W,CHUNG S,LEE Y H.Capacity of the Gaussian Two-way Relay Cannel to Within 1/2 bit[J].IEEE Transactions on Information Theory,2010,56(11):5488-5494. [3] YANG H J,CHUN J,PAULRAJ A.Asymptotic Capacity of the Separated MIMO Two-way Relay Channel[J].IEEE Transactions on Information Theory,2011,57(11):7542-7554. [4] YANG Tao,YUAN Xiaojun,LI Ping,et al.A New Physical Layer Network Coding Scheme with Eigen-direction Alignment Precoding for MIMO Two-way Relaying[J].IEEE Transactions on Communications,2013,61(3):973-986. [5] YUAN Xiaojun,YANG Tao,COLLINGS I B.Multiple-input Multiple-output Two-way Relaying:A Space-division Approach[J].IEEE Transactions on Informa-tion Theory,2013,59(10):6421-6440. [6] KHINA A,KOCHMAN Y,EREZ U.Physical-layer MIMO Relaying[C]//Proceedings of ISIT’11.Saint Pertersburg,Russia:[s.n.],2011:2437-2441. [7] CHAABAN A,SEZGIN A.Multi-way Communi-cations:An Information Theoretic Perspective[J].Foundations and Trends in Communications and Information Theory,2015,12(3/4):185-371. [8] LEE N,LIM J B,CHUN J.Degrees of Freedom of the MIMO Y Channel:Signal Space Alignment for Network Coding[J].IEEE Transactions on Information Theory,2010,56(7):3332-3342. [9] LEE K,LEE N,LEE I.Achievable Degrees of Freedom on K-user Y Channels[J].IEEE Transactions on Wireless Communications,2012,11(3):1210-1219. [10] YUAN Xiaojun.MIMO Multiway Relaying With Clustered Full Data Exchange:Signal Space Alignment and Degrees of Freedom[J].IEEE Transactions on Wireless Communications,2014,13(12):6795-6808. [11] GNDZ D,YENER A,GOLDSMITH A J,at al.The Multiway Relay Channel[J].IEEE Transactions on Information Theory,2013,59(1):51-63. [12] CHAABAN A,SEZGIN A.Cyclic Communication and the Inseparability of MIMO Multi-way Relay Channels[J].IEEE Transactions on Information Theory,2015,61(12):6734-6750. [13] COVER T M,THOMAS J A.Elements of Information Theory[M].New York,USA:Wiley,2006. [14] LOELIGER H A.Averaging Bounds for Lattices and Linear Codes[J].IEEE Transactions on Information Theory,1997,43(6):1767-1773. [15] ORDENTLICH O,EREZ U.A Simple Proof for The Existence of “Good” Pairs of Nested Lattices[C]//Proceedings of IEEEI’12.Eilat,Israel:[s.n.],2012:4439-4453. [16] 何 婵.基于Lattice编码的物理层网络编码[D].成都:西南交通大学,2013.2.1 信道三角化


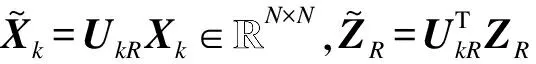
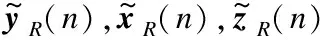
2.2 用户编码方案的设计
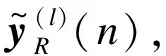






2.3 中继的操作
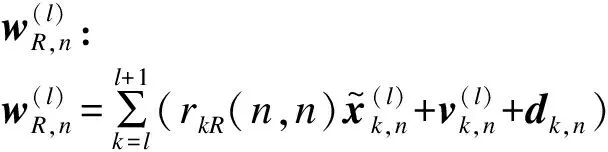


2.4 下行链路用户解码
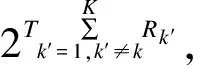
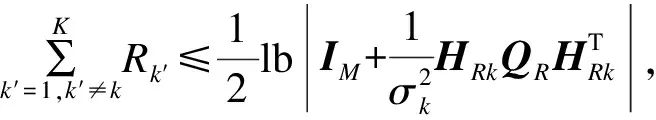
2.5 所提方案的可达速率
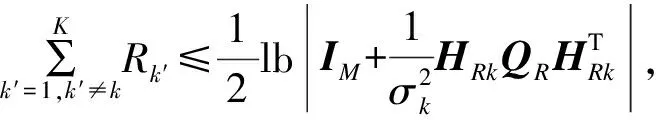
3 渐进近似分析
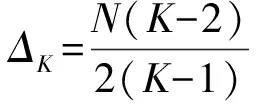

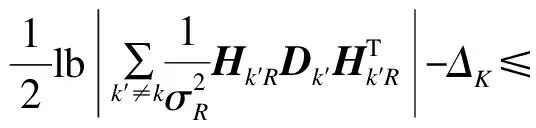

4 各方案对比
4.1 可达速率
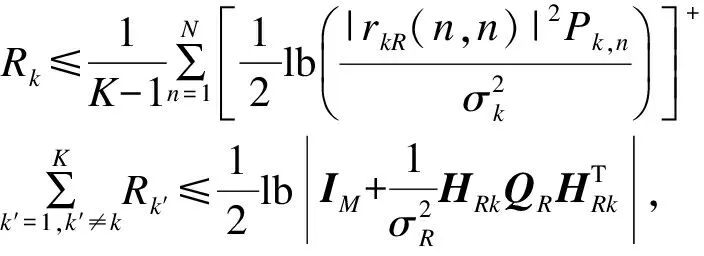
4.2 其他方案
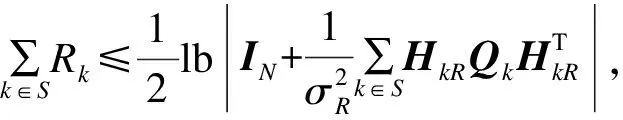
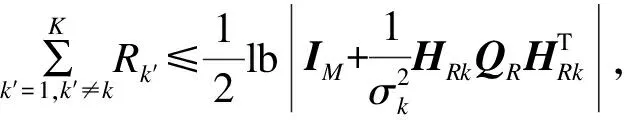
4.3 仿真结果
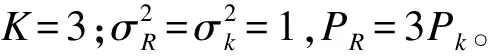
5 结束语
