一道流传已久的习题的错解及纠错

江西省萍乡市萍乡中学(337055)贺江

原题过原点O作两条相互垂直的直线分别与椭圆交于A、C与B、D,求四边形ABCD面积的最小值.

两种解法,两个截然不同的答案,孰对孰错?而且我们在众多解题软件上和某些搜索网站上竟发现这两种解法共存,并且在实际教学中,我们也发现有部分老师也区分不出这两种解法的问题所在.

我们先来看一下椭圆的“离心角”,即参数方程x=acosφ,y=bsinφ中的参数φ.北师大版2014年第4版的选修2-1第66面清楚地提到了这个角,这个角并非椭圆上该点与椭圆中心的连线与x轴正方向的夹角!它不像圆中的圆心角一样!

借助圆心角的概念,我们不妨借助圆中的圆心角设椭圆的“圆心角”概念,椭圆上任意一点与椭圆圆心的连线与x轴方向的夹角,这个夹角用θ表示,即图中∠MOX.易得

意味着OA到OB的旋转角本意是“圆心角”旋转90°,而解法2中OA到OB的旋转角用的是“离心角”旋转90°,两者是否一致呢?

只需验证下OA与OB是否重合垂直.

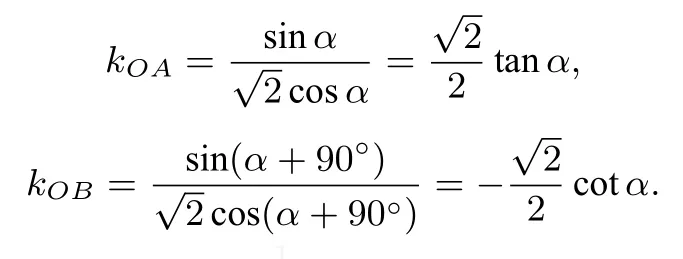
原来解法2中的OA,OB一般情况下并非垂直!

结论解法1为正解,解法2为错解.

下面我们改进一下解法2.

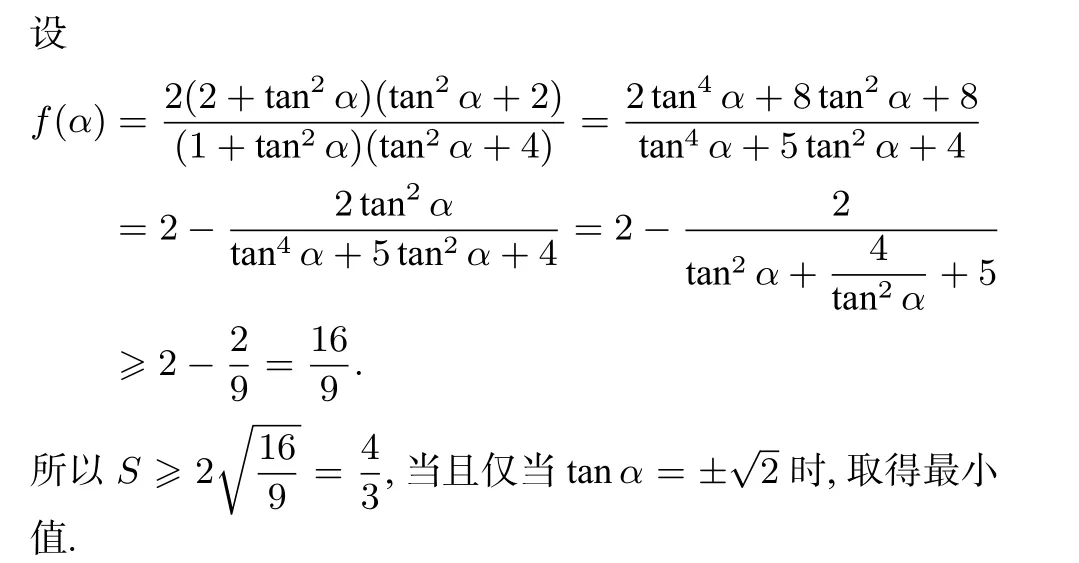
至此,问题已经全部解决.