末段反导防御系统探测误差对拦截效果的影响*

刘锦昌，黄树彩，庞 策，苑智玮，龙振国

（1.空军工程大学防空反导学院，西安 710051；2.解放军95100部队，广州 510405）

0 引言

随着弹道导弹技术的扩散，美国正积极构建弹道导弹防御系统，初步建成了中段和末段防御系统。末段高空区域防御系统（Terminal High Altitude Area Defense，THAAD）也称萨德系统，是美国导弹防御系统的最后一道屏障，负责保护美国本土，盟友及重要军事经济设施免受敌方摧毁［1］。

末段高空区域防御系统主要在大气层内外拦截处于再入段的弹道导弹［2-3］，拦截的过程包括3个阶段：初制导段、中制导段和末制导段。中制导段飞行靠雷达探测弹道导弹的飞行状态并将状态信息传送给反导指挥控制中心（Battle Management and Command，Control，Computer and Intelligence ，BMC3I），反导指挥控制中心根据基于部署的位置和已知的拦截弹动力学性能，以及弹道导弹的状态信息，经过计算的目标与拦截器相遇的空间位置，称作预测拦截点。拦截弹依据不断更新的预测拦截点信息进行中段修正，当拦截弹到达预期位置，姿态控制推进器点火使红外导引头指向目标可能存在的区域完成中末制导交接班。交接班结束后开始末制导，拦截弹在红外导引头探测信息的引导下飞向目标［4］。

中制导段结束时由于雷达探测误差的存在，弹道导弹目标的真实状态信息会与拦截弹获取的信息存在一定的误差。末制导段开始前雷达会将探测信息上传给拦截弹，因为拦截弹本身质量是有限的，携带的燃料也是有限的，所以拦截弹末制导段修正的能力是有限的，雷达探测误差过大的情况下有可能使拦截弹燃料消耗殆尽从而导致拦截失败。在燃料充足的情况下，拦截弹也可能因为雷达探测误差以及导引头探测误差过大而导致脱靶量过大而拦截失败。因此，在保证拦截效果的前提下探测误差应满足的条件是一个亟待解决的问题。

当前，国内外对于探测误差对拦截效果影响方面研究较少，文献［5］建立了末制导拦截仿真模型，对末制导段导引头误差对拦截效能的影响进行了仿真与分析，但是没有考虑雷达探测误差的影响。文献［6］对拦截弹拦截战术导弹的脱靶量进行了仿真，但是没有考虑导引头滤波及能耗的影响。文献［7］分析了脱靶量与能量需求的关系，但是没有考虑探测因素影响。

本文深入分析了末段拦截系统的探测误差及弹目运动规律的基础上，建立了基于比例导引法的末段拦截系统模型，由于模型是非线性模型，因此，将无迹卡尔曼滤波引入模型中对状态变量进行滤波处理。以探测误差为输入，脱靶量及燃料消耗为输出，得到了探测误差与脱靶量和燃料消耗之间的关系，给出了成功拦截时雷达探测误差与导引头探测误差应满足的条件。

1 探测误差及末制导模型

1.1 探测误差分析

1.1.1 雷达探测误差

雷达探测误差图1所示［4］。

拦截弹与目标间的相对速度向量为

雷达探测到的拦截弹与目标间的相对速度向量为

雷达的弹目相对速度探测误差向量为

拦截弹与目标间的真实距离为

雷达探测到的拦截弹与目标间的距离为

雷达的弹目相对位置探测误差向量为

拦截弹与目标间的接近速度表示弹目之间距离变化率，用vcr表示，则

拦截弹在进入末制导之前，雷达会将弹目之间的接近速度信息传送给拦截弹，为末制导拦截弹形成指令提供信息，雷达传送给拦截弹的弹目接近速度大小为vcn，则

从上式可以看出，雷达传送给拦截弹的弹目接近速度并不是真实的弹目接近速度，误差大小受弹目相对位置误差和速度误差的影响。

雷达探测的位置误差和速度误差是均值为零的高斯白噪声，并且在x方向和y方向上的方差相等，设每个方向上的位置误差和速度误差的方差分别为和。

1.1.2 导引头探测误差

拦截弹采用红外焦平面阵列导引头，对视线角进行测量，测量的方程为

1.2 拦截弹末制导段运动模型

中末制导交接班后，拦截弹通过红外导引头探测目标视线角，测量值经过无迹卡尔曼滤波器得到的导引头视线角速度估计值，再经过指令形成装置形成制导指令控制拦截弹飞向目标，完成拦截任务［10］。模型如图2所示：

at和am分别表示目标加速度大小和拦截弹加速度大小，θm，θt，q 分别表示拦截弹度倾角，目标速度倾角及视线角，vmr和vtr表示速度向量vmr和vtr的大小。

拦截弹与目标的相对运动方程为

目标的加速度模型采用一阶时间相关（Singer）模型。

拦截弹末制导采用比例导引法，拦截弹的指令加速度为

N'表示有效导引率值，一般取4，弹目接近速度vcn在末制导开始前由雷达传送给拦截弹，是由滤波得到的视线角速率。

2 基于UKF的模型滤波算法

2.1 状态方程与观测方程的建立

式中：

2.2 UKF滤波算法

因为模型的状态方程是非线性的，所以不能用普通的卡尔曼滤波（Kalman Filter）方法对目标信息进行估计。无迹卡尔曼滤波（Unscented Kalman Filter，UKF）算法采用类似蒙特卡洛（Monte Carlo）的思想，将无迹变换（Unscented Transformation）应用于卡尔曼滤波中，是一种解决非线性滤波问题的非常有效方法［10-13］，具有精度高，速度快，噪声限制少的优点。

状态方程和测量方程改写为

Xk，Yk分别是k时刻的状态矢量，观测矢量，Wk，Vk为k时刻的过程噪声与观测噪声，统计特性为，，。

算法的具体流程如下：

1）初始化

2）根据无迹变换计算Sigma点

3）采样点经过一步预测，可得

4）预测状态的均值与协方差为

5）预测观测的均值为

6）预测观测的协方差为

7）状态与观测的协方差为

8）增益矩阵为

9）状态及协方差更新方程为

3 仿真与分析

脱靶量Miss定义为拦截过程中弹目距离的最小值，即

末制导段拦截弹的速度变化量ΔV可以反映能量消耗的大小，ΔV与拦截弹加速度关系为

tF是末制导段总运动时间，由于拦截弹采用的是姿控轨控的控制方法，用于姿控和轨控的燃料分别占10%和90%。用于轨控的燃料是用于两个方向的，因此，每个方向只能利用总燃料的45%，总燃料质量与用于轨控的燃料的质量的关系为应为

ΔV与轨控能量消耗质量W燃料及拦截弹总质量W总的关系为［10］

式中，Ip表示燃料比冲。

3.1 仿真的初始条件

末段高空防御系统拦截弹的末制导段速度为2 700 m/s，典型目标为射程为3 500 km的弹道导弹，再入段弹头速度4 920 m/s。将拦截弹和弹道导弹再入段弹头看作两个球体，直径分别为0.5 m和1 m，因此，脱靶量小于0.75 m就认为拦截弹与目标发生碰撞［4］。

仿真的初始条件见表1。

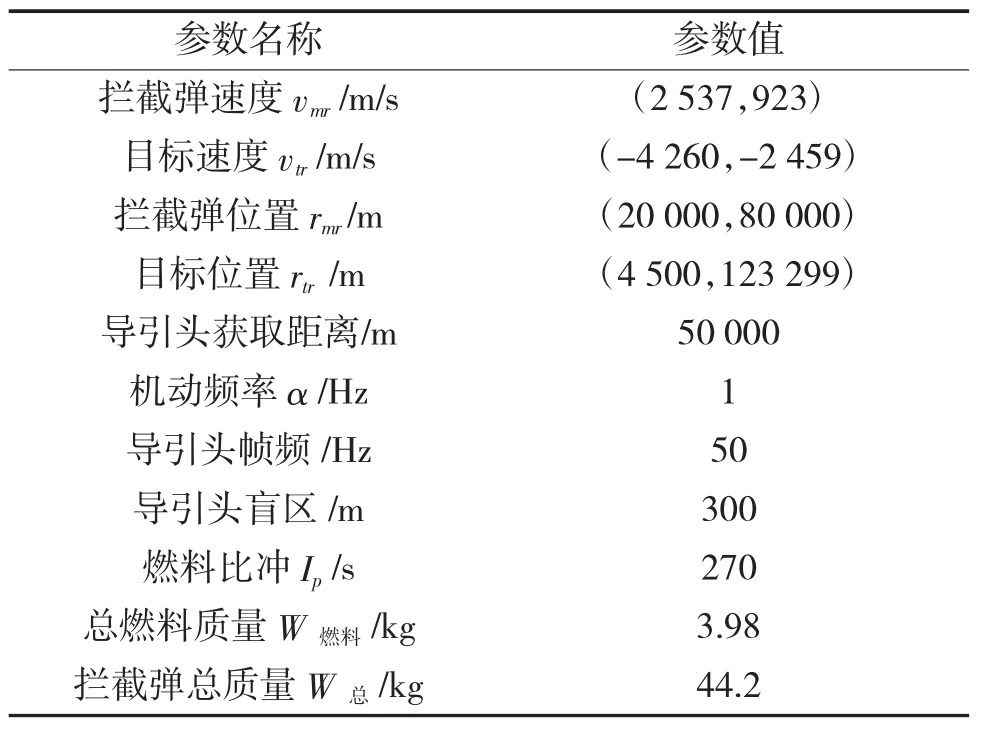
表1 仿真的初始条件

表2 误差初始值

经过100次Monte-Carlo仿真，脱靶量为0.403m，小于0.75 m，能量消耗为1.35 kg，能量足够末制导段拦截使用。说明在上述误差条件下，拦截弹可以成功拦截射程为3 500 km的弹道导弹。下面通过改变位置误差、速度误差和导引头误差大小来研究探测误差对于拦截效果的影响。

3.2 位置误差与速度误差对拦截效果影响

位置误差σr从0 m变化到300 m，将位置误差作为输入变量，得到脱靶量和燃料消耗随位置误差的变化曲线，仿真结果如图4和图5所示。

从图4、图5可以看出，随着位置误差的增大，脱靶量和燃料消耗会呈现线性增大。如果燃料充足，当位置误差达到225 m左右时，脱靶量达到0.75 m，误差再增大会导致拦截失败。当位置误差达到260 m左右时，燃料消耗会达到1.8 kg，误差再增大会导致燃料消耗殆尽从而导致拦截失败。

位置误差σr从0 m/s变化到100 m/s，将速度误差作为输入变量，得到脱靶量和燃料消耗随位置误差的变化曲线，仿真结果如图6和图7所示。

从图6、图7可以看出，随着速度误差的增大，脱靶量和燃料消耗会逐渐增大。如果燃料充足，当速度误差达到60 m/s左右时，脱靶量达到0.75 m，误差再增大会导致拦截失败。当速度误差达到41 m/s左右时，燃料消耗会达到1.8 kg，误差再增大会导致燃料消耗殆尽从而导致拦截失败。

以上分析都是考虑位置误差或速度误差单输入情况下的脱靶量和能量消耗变化情况，综合考虑位置误差和速度误差输入的情况下，脱靶量与消耗的变化曲线，结果如图8和图9所示。

图中横坐标表示速度误差大小，纵坐标表示位置误差大小，图中等高线数值分别表示脱靶量与能量消耗，从图中可以看出成功拦截时速度误差与位置误差必须位于脱靶量为0.75的等高线和能量消耗为1.8 kg的等高线的下方区域。

3.3 导引头探测误差对拦截效果影响

导引头探测误差σq从0μrad变化到1000μrad，将导引头探测误差作为输入变量，得到脱靶量和燃料消耗随导引头探测误差的变化曲线，仿真结果如图10和图11所示。

从图10、图11可以看出，随着导引头探测误差的增加，脱靶量显示平稳增加，当导引头探测误差大于400 μrad时，脱靶量迅速增大，导引头探测误差达到600 μrad时，脱靶量达到0.75 m，误差再增大会导致拦截失败。随着导引头探测误差的增加，燃料消耗总体平稳增加，当误差大于480 μrad时，会因为燃料消耗殆尽导致拦截失败。

4 结论

本文针对末段反导系统探测系统的探测误差对拦截效果的影响问题。介绍了末段防御系统的工作过程，系统分析了雷达误差和导引头的探测误差并在弹目相对运动规律的基础上建立了比例导引的末段拦截模型，接着将无迹卡尔曼滤波引入模型中对导引头探测信息进行滤波处理，从脱靶量和燃料消耗两个方面，研究了探测误差对拦截效果的影响，并且给出了成功拦截时探测误差应满足的约束条件。研究的成果对末段防御系统的探测系统建设具有指导意义。

［1］杨卫丽，锁兴文，田志峰.美国动能反导拦截技术新进展［J］.战术导弹技术，2015，43（2）：6-10.

［2］李运迁，齐乃明.基于零控脱靶量的大气层内拦截弹制导律［J］.宇航学报，2010，31（7）：1768-1774.

［3］程凤舟，万自明，陈士橹.大气层外动能拦截器末制导分析［J］.飞行力学，2012，20（1）：28-41.

［4］HE Y B ，QIU Y.THAAD-Like high altitude theater missile defense： Strategic defense capability and certain countermeasures analysis［J］.Science and Global Security，2003（11）：151-202.

［5］王黎光，景占荣，王玲玲.拦截弹导引头测量误差对拦截效能的影响 ［J］.系统工程与电子技术，2012，34（3）：578-581.

［6］刘庆鸿，陈德源，王子才.动能拦截器拦截战术弹道导弹的脱靶量仿真［J］.系统仿真学报，2002，14（2）：200-203.

［7］周须峰，唐硕，王晓东.空间拦截零控脱靶量与末段制导能量需求的近似计算［J］.火力与指挥控制，2009，34（6）：82-85.

［8］WILHELM D T，PURVIS R K，SINGH A，et al.Force plane arrays（FPAs）for space-based applications［C］//Proc.of the Space Programs and Technologies Conference，1994.

［9］BAILEY R B，KOZLOWSKI L J，CHEN J，et al.256×256 hybird HgCdTe infrared focal plane arrays［J］.IEEE Trans.on Electron Devices，1991，38（5）：1104-1109.

［10］葛致磊，王红，梅王佩，等.导弹导引系统原理［M］.北京：国防工业出版社，2016：270-288.

［11］刘也，余安喜，朱炬波，等.弹道目标实时跟踪中的滤波方法综述［J］.宇航学报，2013，34（11）：1417-1426.

［12］戴洪德，周绍磊，戴邵武.卡尔曼滤波及其实时应用［M］.北京：清华大学出版社，2013：31-35.

［13］董帅军，栗高峰，康传华，等.防空导弹指挥控制系统火力单元动态调整方法［J］.火力与指挥控制，2017，42（4）：105-109.