基于初速雷达数据外推的枪弹外弹道末段计算方法

景春阳，孟祥会，经 哲

（中国白城兵器试验中心，吉林 白城 137001）

0 引言

枪弹因目标小、飞行速度高，弹道为近地低伸弹道，捕获难度大，一般无法对外弹道的全程进行测量，尤其在弹道末段，主要依赖光测手段测量，但获得数据的准确性无法保证。一方面是光测手段易受环境因素影响，干扰较多；另一方面是出现异常数据无法进行判定，缺少其他设备的辅助。

初速雷达威力较小，作用距离较短，一般仅能覆盖枪弹外弹道的初始段，但作为实时跟踪测量设备，能够连续测量出弹丸飞行速度、飞行时间、加速度等多项参数，通过数据筛选能够获得大量高精度数据，结合弹道方程推导计算能够有效获得外弹道末段数据，对获得的光测数据起到较好的补充测量和判定作用。

1 雷达基本测量原理

雷达天线发射固定频率的连续波信号，接收目标反射的回波信号，与发射信号混频后提取出多普勒信号。多普勒信号在信号处理单元进行放大和数字化。数字化多普勒信号保存在内部存储器中，通过快速傅立叶变换（FFT）和数字信号处理解算出目标速度［2］。

根据多普勒效应，目标相对雷达运动产生的多普勒频率为：

其中f0为雷达发射连续波的频率，vr为目标相对雷达运动的速度，即径向速度，c为电磁波传播速度。

由于 vr＜＜c，可忽略分母中的 vr，这时有

此式称为经典的雷达测速方程。由此可见，只要测得fd（f0和c是已知的），即可由式（2）求出径向速度vr。

目前雷达的测速精度一般都可高于0.1%，测试系统的精度也可达到10-6s，通常可以认为雷达测量的v-t曲线是精确的，从中可以提取出初速v0、径向速度vr、时间t及加速度a。雷达测试数据示例如图1所示。

2 测量数据筛选

雷达在进行测试时，一些测试数据误差较大，误差来源主要有两种情况，一种是受雷达技术条件限制，在远距离及部分点处信噪比较低，精度较差产生误差；另一种是受雷达使用条件限制，实际使用时无法与枪口十分靠近，且在雷达波束内受非目标物体干扰影响，一些测量点数据明显偏离弹道，产生误差。

2.1 剔除信噪比较低的数据

根据雷达实测瀑布图，如图2所示，受地杂波干扰，雷达测试时的信噪比会随着距离增大逐渐降低，通常认为在信噪比S/N＞10 dB时认为数据精度较高，需剔除不满足该条件的数据。

2.2 剔除偏离弹道的数据

出于雷达安全防护考虑，其位置一般无法与枪口十分靠近，这样目标相对雷达运动的径向速度vr就不是目标运动的弹道切向速度v（绝对速度），而是弹道切向速度v在雷达观测方向上的投影［3］，如图3所示。

这表明，径向速度vr需通过速度转换才能得到切向速度v。而由于测量雷达相对枪口位置坐标的方法无法保证足够的精度，会造成切向速度v的计算误差，这一误差在初始段较大，但随着弹丸与枪口距离的增大而减小，当距离足够远时，可以认为v≈vr。

另一种情况是受非目标物体的干扰，一些速度值会产生明显异常，这些数据对拟合弹道曲线的影响不大，但在弹道计算中会明显降低计算准确度，因此，也必须予以剔除。

3 弹道外推计算方法

3.1 弹道系数计算

弹道系数c是表示弹丸的本身特征（形状、尺寸大小和重量）对弹丸运动的影响［1］。

其中i为弹形系数，d为弹丸直径。

弹道系数是弹道计算的重要参数，在外弹道学中计算弹道系数主要有两种方法，分别为加速度法和动能法［1］。

3.1.1 加速度法

加速度法是指射击时弹丸速度的变化率即加速度等同于弹丸飞行时所受空气阻力：

其中a为实测加速度值，g为重力加速度，F（v）表示关于速度v的阻力函数。

F（v）在 400≤v≤1 400 的经验公式为：

该经验公式误差小于0.6%。

3.1.2 动能法

动能法就是指在水平射击时弹丸动能的减少等于弹丸克服阻力所作的功，即：

这两种方法均可计算弹道系数，但加速度法适用范围更广，能够用于多种仰角射击条件的计算，且现有雷达数据就可完成；动能法仅适用于平直弹道，使用雷达数据计算时需要估算距离L1，2的值，同时还需要弹丸的特征数据，计算较为复杂。

根据雷达测量数据的特点，选择加速度法来计算弹道系数c，同时，因雷达测量数据量较大，可以得出不同速度下的弹道系数，作弹道系数-速度的拟合曲线c（v）-v，根据速度大小选择相应的弹道系数，进一步提高测速精度。

3.2 计算弹道

根据外弹道学，在 v0、θ0、c 给定时，弹道已唯一确定［1，4］。

根据方程组及起始条件（t=0 时，θ=θ0，v=v0，x=y=0）可以知道：任意时间t时的弹道诸元v，θ，y，x一定都是起始条件（v0，θ0）与包含在方程组内的弹道系数c和自变量t的函数，即：

当c，v0，θ0给定时，任意点弹道诸元仅由时间t确定。就是说，任意给一个时间t，与此相应的弹道诸元就可以确定，因而弹道就可以完全确定。通过级数解法，v，θ，y，x 4个参数都可以计算得出，为计算终点弹道参数，即已知距离s，计算时间t，高度y，弹道倾角θ，速度v，其他参数均可通过这几项参数得出。

距离s处的飞行时间：

距离s处的弹道高：

距离s处的弹道倾角：

距离s处的速度：

根据式（9）～式（12）可以推导出其他所需弹道参数。

4 实际数据验证

以某型枪弹为例，有效射程400 m。初速约为870 m/s，射击方式为平射（忽略跳角影响，可认为θ0≈0），雷达天线高h=1.21 m，测试有效距离约为100 m，弹温为标准温度。

按P＜0.1%取值，则对 t＜8.876 ms的数据剔除。

按S/N＞10 dB取值，则剔除信噪比低于10 dB的数据，选取截止时间，如下页图5所示。

对筛选后的雷达实测数据按式（9）计算弹道系数，其中部分计算结果如下页表2所示。

表1 相对误差P的计算表格

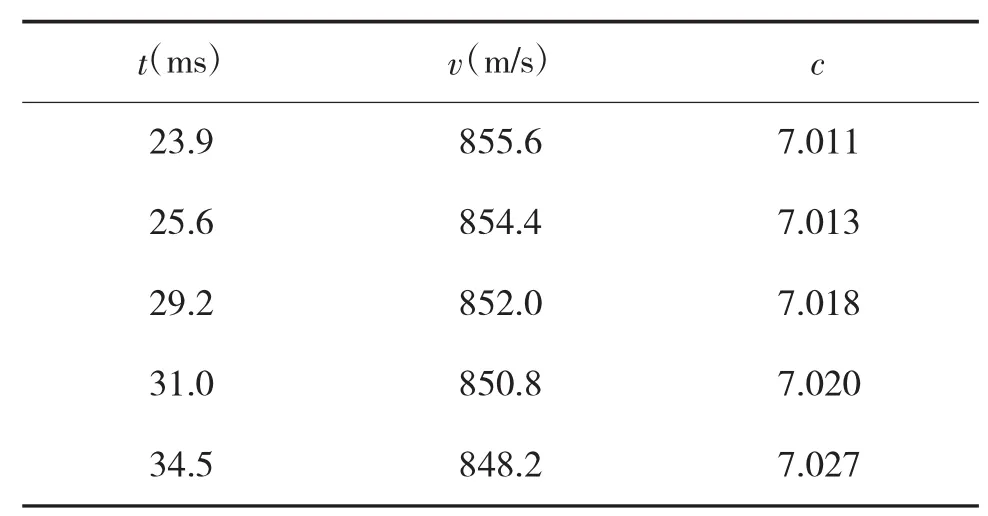
表2 弹道系数计算

从表中可以看出弹道系数会随着速度的变化而变化，作c-v曲线拟合，，如图6所示。

求出 c（v0）=6.966 5。

根据已有数据对式（9）和式（12）进行验证，联立求出

根据式（13）计算速度并与实测速度对比求相对误差，如表3所示。

表3 速度验证数据

经计算，在保证测速精度满足0.1%要求下，可以将弹道延伸计算至400 m左右，即在现有雷达已测约100 m的距离下保精度延伸了300 m，从而获得弹道末段数据。

通过上述已获得的数据计算该型枪弹在400 m处弹道参数，即s=400 m，得到：

由式（9），计算飞行时间 t=544.6 ms；

由式（10），计算弹道高y=0.012 m；

由式（11），计算弹道倾角 θ=0.007 rad；

由式（12），计算速度 v=544.4 m/s。

使用光测设备实测400 m飞行时间为547.8 ms，通过对比可知使用该方法计算弹道末段参数的精度较高。

5 结论

通过对初速雷达测量数据的进一步筛选，根据弹道方程建立外弹道初始段与末段之间关系，从而得到外弹道末段的各项参数，包括弹丸飞行距离、飞行时间、弹道倾角、飞行速度等，实践证明，这种方法是可行的，虽然在精度上较光测设备尚有一定差距，但却可弥补易受环境干扰、捕获率低等缺陷：一方面当光测设备失效时，可以起到良好的补充测量作用；另一方面，对于测试中出现的异常数据无法判定异常原因时，可以作为判定依据。

这种方法拓宽了初速雷达测量数据的应用范围，提高了数据利用率，为测试数据的准确性判定提供了依据。

［1］浦发.外弹道学［M］.北京：国防工业出版社，1980.

［2］丁鹭飞，耿富录.雷达原理［M］.西安：西安科技大学出版社，2002.

［3］周旦红.多普勒测速雷达速度转换的误差分析［J］.哈尔滨工程大学学报，2007，28（1）：93-96.

［4］朱艺，肖兵，林傲，等.弹道导弹威胁估计模型构建［J］.火力与指挥控制，2016，41（2）:117-123.