群目标侦察航迹规划方法*

朱创创，梁晓龙，何吕龙，景晓年

（空军工程大学空管领航学院，西安 710051）

0 引言

为实现更高效的资源共享及更紧密的协同配合，集群作战将是未来战争的主要特征之一。这不仅体现在空中进攻呈现出集群［1-3］的形态，需要打击的地面目标也会以目标群的形式出现。在实际作战中，一旦雷达发现无人机便会采取相应对策，如发射导弹进行拦截等。因此，侦察无人机滞留防御方雷达探测范围内时间越长，被其摧毁的可能性就越大。这就需为无人机规划最佳的航迹，以保证侦察无人机滞留防御方雷达有效探测范围内的时间总和最小，即完成侦察任务的总路径最短。

当前有很多关于无人机航迹规划方法的研究，即在一定的环境下，寻找无人机从起始点到目标点满足某种性能指标的最优飞行路线［4］。如传统的启发式 A* 算法［5］，Voronoi图［6］，Dijkstra 算法［7］，混合整数线性规划方法［8］。此外，仿效力的作用形成空间力场进行规划的人工势场法也是有效进行航迹规划的方法。近年来群智能算法逐步获得了关注，例如遗传算法［9］、蚁群算法［10］、模拟退火算法［11］等在航迹规划中发挥了重要作用。

当目标数量较少时，这些点对点的航迹规划方法都具有令人满意的效果。但当目标数量较大时，采用这些方法的计算量将随目标数量的增加呈指数增长［12］，算法复杂度大大增加。为此，需要对多目标侦察的航迹规划方法进行研究，以适应未来作战的需求。在实际作战中，执行侦察任务的无人机通常挂载的是具有较大作用带宽和距离的广域搜索传感器，即目标落入传感器观测带宽内即可完成对目标的侦察，如图1所示。当需要获取某一区域的全面信息或者对特定区域进行搜索时，点对点的航迹规划方法已不能满足任务要求，因此，就需要采用覆盖航迹规划技术。覆盖航迹规划指在满足某种性能指标最优的前提下，规划出一条能够覆盖探测区域的最优飞行路线［13］。本文针对群目标的侦察航迹规划问题，提出先进行聚类分析将目标按照位置分成多个子目标群，再采用群间航迹规划和群内覆盖航迹规划相结合的分层规划方法。由于本文采用群间航路和群内航线双层规划体制，在此给出航路规划和航线规划的定义：

定义1 群间航路规划是指将每个目标群看作一个整体而进行的全局的路径规划。

定义2 群内航线规划是指在每个目标群内完成侦察各个目标点时无人机的局部路线规划。

本文所指航路和航线最大的区别就在于，航路是群间的、全局的，而航线则是群内的、局部的。

1 目标聚类

防御方雷达部署时会用空域覆盖系数来衡量雷达网的探测威力，表征雷达网空域覆盖的连续性和严密性。在雷达组网时要尽量增大该系数，同时确保较好的威力衔接［14］，通常会相对分散并将防御区的目标群全部覆盖。若雷达是全向覆盖的，则可将雷达看作其探测范围内所有目标的位置中心。

假设需要侦察的目标点数量为N，其中NP为雷达基地。基地集表示为，基地的坐标为。

2 群间航路规划

根据假设，将每个子目标群作为整体当成一个航路点，总共有NP个子目标群，出动一架携带某型传感器的无人机。则群间航路规划转化为NP个节点的TSP问题。它是指给定NP个目标点，现需找出一条路径，使得侦察飞机从某一起点进入经过不同的路径后返回起飞基地，每个雷达基地必须被访问且只能访问一次的总路径最短。

st.

式（2）、式（3）表示所有目标点都被侦察到，且最多被侦察一次。为保证无人机滞留在雷达探测范围时间最小，无人机在开始进入雷达探测范围执行任务和完成对所有目标群侦察后离开时均沿探测区径向飞行。

3 群内航线规划

文中提到的携带的传感器是以一定带宽进行扫掠式侦察，那么群内侦察就是典型的区域覆盖问题。扫掠式区域覆盖是以一定的方式越过目标区域，并能够保持单位时间内最大检测率和单位区域内最小未检测数量之间的平衡，如扫雷、巡航等。针对这一问题要分两步解决，首先寻找子目标群形成的最小凸多边形，其次是在最小凸多边形中解决机动次数最少且路径最短的航迹覆盖问题。

本课题组前期研究还发现，一种天然来源（主要是十字花科植物萝卜）的异硫氰酸酯类化合物莱菔素（sulforaphene，分子式为C6H9NOS2）LFS-01能够抑制多种类型的淋巴瘤细胞增殖，并且套细胞淋巴瘤对该化合物的敏感性更强[15]。在此基础上，本研究进一步分析套细胞淋巴瘤中CRM1的表达情况，并探讨LFS-01抑制套细胞淋巴瘤细胞增殖的具体机制。

3.1 寻找最小凸多边形

求解包含子目标群内已知目标点的最小凸多边形，可以通过递归地寻找最大内角从而寻找到最小凸多边形的边界。利用Delaunay三角剖分算法，寻找所有剖分出的三角形中仅出现了一次的边界，这些边界就是其最小凸多边形的边界。最后再通过边界跟踪，即可锁定最小凸多边形的边界顺序，从而求解该问题。该算法的具体步骤如下：

Step1：利用Delaunay函数，对所有目标点进行Delaunay三角剖分处理，Delaunay函数的返回值是N*3的矩阵，其中N为剖分出的三角形个数，3为每个三角形的3个端点的序号。

Step2：根据triangles矩阵，提取出所有Delaunay三角剖分时所连接的边。依次扫描triangles矩阵的每一行，将Delaunay三角剖分时所连接的边添加到一个新的矩阵中，最后构成一个M*2的矩阵，其中M是一共所连接的边的条数。

Step3：显然，直观可见，最小凸多边形上的边应该仅在以上矩阵中出现一次，因此，将以上矩阵中那些出现次数超过一次的边全部去掉，最后保留的便是最小凸多边形的边。

Step4：根据最小凸多边形的边，很容易得到构成最小凸多边形的结点的顺序，从而解决问题。经聚类后形成目标群A01所确定的待覆盖区域凸多边形如图2所示。

3.2 区域覆盖扫略算法

文献［15］中已经证明从能量、路程、时间角度，理论上证明转弯过程比直线平飞过程效率低，并给出了在整个群内侦查过程中减少转弯机动的凸多边形覆盖航迹规划方法。本文在此基础上提出区域覆盖扫掠算法，即沿着平行于最小高度的边飞行扫掠一次后，将覆盖目标点去掉后重新求出剩余点的最小凸多边形，再次扫掠的群内侦查策略，使转弯次数最少、侦察航迹最短。算法流程步骤如下，流程图如图3所示。

Step1：算法开始，求解包含目标群内未被侦察目标的最小凸多边形。

Step2：沿凸多边形最小高度所在边扫掠一次。

最小高度的定义及求解过程如下：

Step3：判断是否群内所有目标点已被侦察，若是，则退出侦察前往下一目标点，否则返回Step1。

所以扫略方向为达到最小高度的边的平行方向，最大扫略次数为

其中，Bw为传感器的扫掠带宽，H1为包含群内所有目标的最大凸多边形的最小高度表示向上取整。

4 仿真验证

为验证提出方法的可行性，以包含68个目标点（其中包括10个雷达站）的目标群为例进行仿真验证。首先以雷达为中心将目标群进行聚类，可得10个子目标群，如图4所示，其中大圆表示雷达的探测范围。

针对目标群聚类划分的结果，在群间进行侦察路线规划。用GA算法求解该旅行商问题得到的最短路径为A01-A02-A08-A09-A03-A04-A10-A07-A05-A06，如图5（a）所示，滞留在雷达探测范围的航路长度为891.83 km。加上无人机的启用成本（进出雷达探测范围的距离），在探测范围内的路径长度为1 031.83 km。若无人机基地位于P01，如图6（b）所示，在经过A02时局部调整路线即不经过其探测范围,得到此时的路径长度为1 533.54 km.

针对子目标群内的航线规划，取扫描宽度Bw=8 km，以无人机在子目标群A04、A10内的侦察航线规划为例，表1为两子目标群目标点坐标。在对 A04目标群规划侦察时首先确定 01、02、03、07、08、09的最小凸多边形以及最小高度09到01、02的距离,然后平行于01、02所确定边扫掠，一次扫掠之后将 08、09、10、01、02 覆盖,接着将沿 03、04、05、06确定的最小凸多边形中04、05所确定的边扫掠,一次可覆盖完目标，航线如图6（a）所示。针对子目标群A10扫掠时，一次可将5个目标点覆盖，航线如图6（b）所示。总的航线长度为各个子目标群内的航线之和，共349 km。

表1 子目标群内的目标点坐标

表2为10个目标群内的扫描次数以及路径长度，结合群间和群内航迹规划结果，该型无人机携带传感器完成所有目标的侦察任务，滞留在防御方雷达探测范围的总距离为1 380.83 km。在群间转弯次数做到了最少，总飞行路径最短。

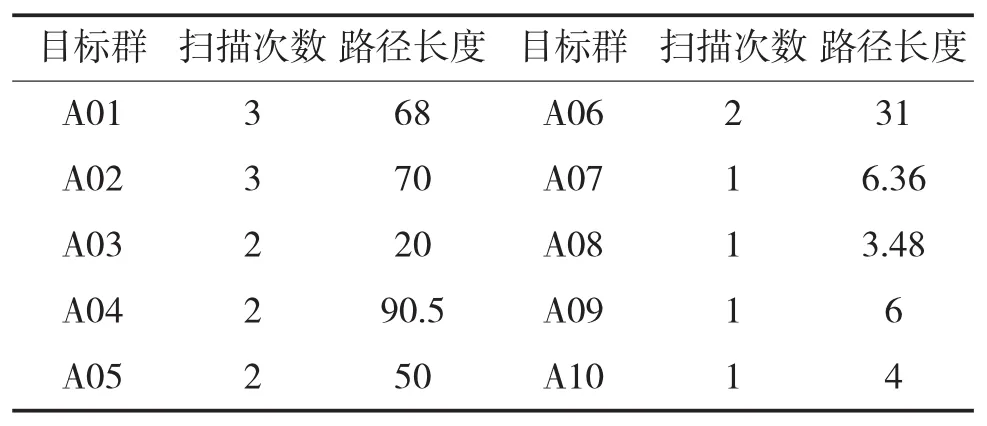
表2 目标群内的路径长度

5 结论

本文针对集群多基地多目标航迹规划问题，提出了先进行聚类分析将集群划分为若干个子群，再分别对群内、群间航迹规划分层处理的方法。仿真结果表明，该方法能有效减少目标侦察时的转弯机动次数并使得无人机总飞行路径最短，验证了该方法的有效性。该方法具有降低计算量，减小算法复杂度的优点，提高了群目标侦察航迹规划的效率。

然而，实际战争中存在许多不确定的威胁，单架无人机单基地起飞完成侦察任务成功率不高。因此，航空集群多基地起飞的航迹规划问题，将是下一步的研究工作。

［1］SHIMA T，RASMUSSEN S.UAV cooperative decision and control：challenges and practical approaches［M］.Philadelphia：Society for Industrial and Applied Mathematics，2008.

［2］梁晓龙，李浩，孙强，等.空中作战发展特征及对策［J］.空军工程大学学报（军事科学版），2014，14（3）：4-7.

［3］牛轶峰，肖湘江，柯冠岩.无人机集群作战概念及关键技术分析［J］.国防科技，2013，35（5）：37-43.

［4］BORTOFF S A.Path planning for UAVs［C］//Proceedings of the American Control Conference，2000：364-368.

［5］YANG X，DING M Y，ZHOU C P.Fast marine route planning for UAV using improved sparse A*algorithm［C］//InternationalConferenceon Geneticand Evolutionary Computing，China，2010：190-193.

［6］ MCLAIN T W，BEARD R W.Trajectory planning for coordinated rendezvous of unmanned air vehicles［C］//Proceedings of the AIAA Guidance，Navigation and Control Conference ，2009（8）：303-305.

［7］EPPSTEIN D.Finding the k shortest paths［J］.SIAM Journal of Computing，1998，28（2）：652-673.

［8］JEAN B，ABDESLEM B，ABDELHAMID B，et al.A new mixed-integer linear programming model for rescue path planning in uncertain adversarial environment［J］.Computer and Operations Research，2012，39（12）：3420-3430.

［9］ EUN Y， BANG H.Cooperative task assignment/path planning of multiple unmanned aerial vehicles using genetic algorithms［J］.Journal of Aircraft，2009，46（1）：338-343.

［10］WANG Z H，ZHANG W G，SHI J P，et al.UAV route planning using multi objective ant colony system［C］//2008 IEEE Conference on Cybernetics and Intelligent System，2008，21（24）：797-800.

［11］ZHANGY，GONGDW，ZHANGJH.Robotpathplanningin uncertain environment using multi-objective particleswarm.optimization［J］.Neurocomputing，2013（3）：172-185.

［12］沈林成，陈璟，王楠.飞行器任务规划技术综述［J］.航空学报，2014，35（3）：593-606.

［13］AGARWAL A，LIM M H，ER M J，et al.ACO for a new TSP in region coverage［C］//IEEE/RSJ International Conference onIntelligentRobotsandSystems，2005：1717-1722.

［14］王中杰，李侠，周启明，等.基于多约束条件遗传算法的雷达网优化部署［J］.系统工程与电子技术，2008，30（2）：265-268.

［15］陈海，王新民，焦裕松，等.一种凸多边形区域的无人机覆盖航迹规划［J］.航空学报，2010，31（9）：1802-1808.

［16］宋斌斌，金慧琴，李启超.改进A*算法在突防航迹规划中的应用［J］.兵器装备工程学报，2016（7）：85-89.