数学教学应尊重学生的形象思维

广西岑溪市第二小学(543200)

李志梅

常听到不少教师抱怨：“如今的学生越来越难教了，而且越来越不会思考问题。”由于教师只是年复一年地教着，没有站在学生的角度思考问题，所以学生越来越没有兴趣学习。布鲁纳也说过：“没有真正经历知识获取的过程，而仅仅只是单纯地去接受知识的话，那么这种知识的获取就不能真正激发学生的兴趣。”这说明学生没有经历知识产生、形成、发展的过程，对所学知识不会记忆深刻。因此，教师就成为学生学习的引路人，使学生对所学知识产生兴趣。

例如，教学将长方形变成平行四边形这一知识点时，我在学生操作后提问：“这时长方形的周长和面积将发生怎样的变化？”由于学生对长方形和平行四边形的周长、面积计算十分明确，所以我直接出示以下演变过程，让学生通过观察思考长方形和平行四边形前后周长、面积的变化情况。

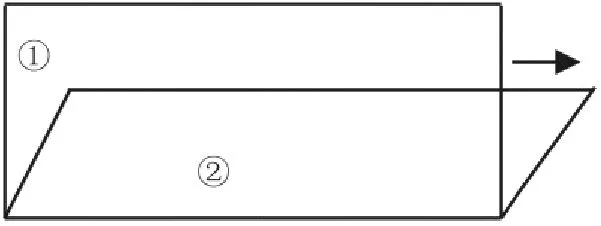
(长方形拉成平行四边形)

(平行四边形拉成长方形)

这样教学，整个课堂效果还是不错的，我认为学生已经理解了长方形和平行四边形前后周长、面积的变化关系。于是我让学生进行练习，结果有近三分之一的学生无法正确求出答案，我不禁愣住了。面对这一现状，我不禁思考：“难道学生不理解？难道自己的讲解不到位？”为了解决疑惑，我让学生准备三根同样长的吸管和一条长细线，把其中一根吸管对半分，再和另外两根长吸管拼接成一个长方形，然后用线从中穿过并打结，做成一个活动的长方形，再将活动的长方形拉成平行四边形。在反复操作中，有学生说道：“长方形和平行四边形的周长不变，都是吸管的总长度。”学生的这一回答，让我又惊又喜：“多么重要的发现啊！学生在操作中终于得出正确的答案。”我追问：“那长方形和平行四边形前后的面积又怎样变化呢？”问题提出后，学生顿时安静下来，都专注地思考着。我在巡视中发现有的学生用尺子比较长方形的宽与拉成的平行四边形的高的长短，有的学生则与同桌展开讨论“在直角三角形中，斜边最长，拉成的平行四边形的高肯定比长方形的宽短，底相当于长方形的长，所以拉成的平行四边形的面积比原来长方形的面积小”。“太不简单了！”我马上让全班学生分享这个发现并再次演示和讲解：“拉成的平行四边形越扁，它的面积就——”学生迫不及待地齐声回答：“越小。”最后，学生在不断的操作中得出结论：“当长方形拉成平行四边形时，周长不变，面积变小，拉成的平行四边形越扁，它的面积就越小；平行四边形拉成长方形时，周长不变，面积变大。”终于，这让学生困惑的问题在直观操作中得到了解决。此外，为了让学生对“把一个平行四边形沿着高剪开拼成一个长方形”与上题进行区分，我特别要求学生实践操作，通过对比得出“平行四边形沿高剪开拼成一个长方形时，周长变小，面积不变”的规律。

如练习中有这样一道题：“在一个平行四边形中，两条邻边的长度分别为10厘米和7厘米，其中一条高为9厘米，这个平行四边形的面积是( )平方厘米。”通过实际调查发现，这一题对于别的班级来说，几乎都是失分严重的题，大部分学生都认为应用10×9计算出平行四边形的面积，而没有考虑高与斜边的关系。也就是说，学生根本没有考虑直角三角形中斜边最长的规律。由于我班学生经历了自己探究、感悟所学知识的过程，绝大部分都能正确计算，这再次说明学生经历操作探究的过程，对所学知识的理解会更深刻，记忆更牢固。

又如，教学“甲、乙共有60张邮票，甲给乙12张后，两人邮票一样多，原来甲、乙各有几张邮票”这类题目时，大部分学生都这样解答：因为60-12=48(张)、48÷2=24(张)，所以甲、乙各有60-24=36(张)邮票。面对学生出现的错误，我不禁思考：“为什么学生不懂得正确找出题中相差的数量？”为了让问题得到正确解决，我从学生感兴趣的钱数入手，指名两个学生上台来按要求给钱，并让学生反复操作。结果，学生发现没有人会把自己多出的部分钱全部给对方，都知道把多出的钱的一半先留给自己，另一半给对方，这样才能使两人的钱数相等。通过这样的操作活动，再回到具体的练习中，学生解答的正确率明显提高了。因此，在实际教学中，教师若有一双善于发现错误的慧眼，能有效利用学生的错误资源，引导学生在错误中吸取教训，这样的错又何妨？

总之，小学生的思维以形象思维为主，所以教师应与学生处于同一思维高度，根据学生的认知规律、实际情况和具体的教学内容，激发学生的学习兴趣，引导学生不断深入探究，使教学变得更加有趣、更有效。