橡胶履带轮静态接地压力测试与建模

赵子涵，穆希辉，郭浩亮，吕 凯，杜峰坡

0 引 言

橡胶履带轮作为一种兼具轮胎和履带特点的行走系统，能够在不改变车辆主体的条件下，通过进行轮履互换增大接地面积、减小接地压力、提高通过性[1-2]。基于以上优良特性，橡胶履带轮逐渐在农用机械、工程机械以及军事等领域得到广泛应用。橡胶履带轮的接地压力分布不仅与履带车辆的牵引性能、转向性能和通过性等相关，同时也影响着土壤的压实程度。准确预测橡胶履带轮接地压力分布，对于指导其结构设计、研究其各项性能以及判断土壤压实风险都具有重要意义。

一般情况下，履带车辆沿履带长度方向的接地压力呈多峰值非线性分布。国内外学者建立了诸多模型以预测履带车辆的接地压力分布规律，如国外的 Garber等[3]提出了一种履带车辆接地压力静态分布的数学模型，能够定量分析车辆参数和土壤参数对接地压力分布的影响；Okello等[4]提出了一种履带车辆在松软农田上的接地压力分布模型，模型考虑了土壤受到重复施载影响，对土壤参数进行了修正；Arvidsson等[5]分别对履带车辆和轮式车辆在松软地面上的接地压力分布进行测试，并根据接地压力推导了不同深度土壤的应力和饱和导水率；Keller等[6]利用前人测得的履带车辆接地压力试验数据，提出了一种简易的履带车辆接地压力分布预测模型，该模型参数只考虑了履带车辆的结构参数，因此该模型在一定条件下具有很强的实用性，但由于模型没有考虑土壤参数，因此也具有一定的局限性；国内的陈秉聪等[7]提出了履带式拖拉机在松软地面上的接地压力动态分布的数学模型；杨士敏[8]推导了接地压力呈矩形、梯形、多峰值正弦分布时的数学模型，并据此计算了履带车辆在砂土上的附着力；许焰等[9]根据接地压力测试结果，建立了简单函数形式的接地压力数学模型，并据此推算了履带车辆的牵引力；王红岩团队[10-12]考虑转向离心力对履带车辆接地压力的影响，建立了转向工况下的接地压力数学模型，对履带车辆的转向性能进行了分析和试验；Tang等[13]将履带车辆的接地压力分布简化为梯形分布和双梯形分布，结合经典地面力学，提出了一种高速履带车辆的侧向动力学模型。以上用于预测接地压力分布的数学模型大多是在 Bekker提出的压力-沉陷经验公式基础上，综合考虑履带结构参数和土壤参数后提出的，一般用于履带车辆牵引性能和土壤压实等方面的研究。但这些模型中通常包含较多参数，尤其是其中涉及的土壤参数需进行土壤承压和剪切试验获得，影响了模型的进一步推广应用。

此外，橡胶履带轮一般采用独特的三角形构型，其整体结构、负重轮排列以及履带尺寸等都区别于整体式橡胶履带和其他四轮一带系统，因此橡胶履带轮接地压力分布规律与其他履带车辆存在差异。目前，国内外针对橡胶履带轮接地压力分布的研究较少，亟需相关理论和试验数据为其进一步设计改进提供依据。本文以橡胶履带轮为研究对象，通过测试其在坚实地面和松软地面条件下的接地压力，总结其分布规律，提出一种简易有效的橡胶履带轮接地压力分布数学模型，最后基于该模型推导计算橡胶履带轮在坚实地面和松软地面的静态转向阻力并进行试验验证，考察该模型对转向性能研究的适用性，以期为橡胶履带轮性能分析和结构优化设计提供理论支持。

1 橡胶履带轮接地压力测试

1.1 橡胶履带轮结构介绍

本文研究对象是笔者单位以全地形装卸车为配套对象自主研发的SLD01橡胶履带轮，主要由驱动轮、负重轮、橡胶履带、张紧装置、助力转向装置以及基架组成，如图1所示。其中，沿接地长度方向上均匀布置有5行4列的负重轮和1行4列的导向轮，负重轮和导向轮结构尺寸相同，负重轮半径为 100 mm，负重轮行间轴距为250 mm。履带为无芯金式橡胶履带，采用全地形一字花纹[14]，履带接地长度为1 250 mm，接地宽度为600 mm。

图1 橡胶履带轮Fig.1 Rubber tracked assembly

1.2 接地压力测试方法

履带车辆接地压力的一般测试方法为在履带下方土壤浅表层预埋多个压力传感器，通过压力传感器测得履带车辆的接地压力分布。此方法虽然简单易行，但测量精度取决于压力传感器的预埋位置和数量，实际测量时，压力传感器往往不能覆盖全部接地区域而影响测量精度。本文采用Tekscan压力分布测量系统[15]，通过在地面铺设压力感测片来测量橡胶履带轮接地压力。每块感测片的测量面积为435.9 mm×368.8 mm，而该橡胶履带轮实际接地面积约为1 250 mm×600 mm，因此在测试中将6块感测片进行拼接。为避免测量过程中感测片表面薄膜产生滑移破坏，采用橡胶薄片对其进行保护。

为测量不同载荷时橡胶履带轮的接地压力，将整车的伸缩臂伸长，使得在总质量不变的情况下车辆前桥载荷增加，从而使左、右前轮的载荷增加。本文以右前轮接地压力为试验对象，当前桥载荷增量为 0、0.5、1.0、1.5 t时，对应的右前轮载荷为 2 241、2 498、2 755、3 011 kg。

测量时，首先将车辆驶于待测区域，使用千斤顶将前桥顶起，将处理后的感测片置于右前轮下方，缓慢释放千斤顶，使右前轮垂直落于感测片上，通过采集卡将感测片测得的数据实时传送到 PC机，由内置软件Tirescan进行数据记录、处理和导出。通过调整伸缩臂位置，改变右前轮载荷，在坚实地面和松软地面上，分别测量在4种载荷下的接地压力，每种条件下试验3次取均值。在测量橡胶履带轮在松软地面的接地压力时，为避免土壤受到重复施载的影响，每次测量后，需将待测区域重新平整，并使用土壤承压剪切仪测量土壤参数，确保每次试验地面条件一致。图 2所示分别为橡胶履带轮在坚实地面和松软地面的接地压力测试现场。

图2 接地压力测试现场Fig.2 Test site of ground pressure

2 测试结果分析

图 3所示为不同载荷时橡胶履带轮在坚实地面和松软地面的接地压力分布。定义接地长度方向为履带纵向，接地宽度方向为履带横向。

图 4所示为坚实地面和松软地面条件下履带纵向中部的接地压力分布。

由图3和图4可知，橡胶履带轮在坚实地面的接地压力分布特点[5,16-17]：1）在纵向上，橡胶履带轮接地压力类似于整体式履带呈多峰值非均匀分布，接地压力集中分布于负重轮下方，负重轮之间的履带接地压力几乎为0；同时其接地压力峰值类似于轮胎呈钟罩型分布，即中间峰值较大，向两边逐渐减小，同时载荷越大，各峰值大小分布越均匀。2）在横向上，橡胶履带轮接地压力连续分布于履带下方，并呈钟罩型分布。

橡胶履带轮接地压力呈现以上分布规律，主要因为其负重轮布置方式与整体式履带系统类似，因此在纵向上其接地压力呈现多峰值非均匀分布。但橡胶履带轮履带接地段的长宽比较大，一般整体式履带长宽比约为1.28～1.62[18]，而该橡胶履带轮的履带接地段长宽比约为2.08，因此接地压力峰值又类似于轮胎接地压力分布。

橡胶履带轮在松软地面的接地压力与其在坚实地面的分布规律基本相同，主要区别在于在松软地面条件下，橡胶履带轮在纵向上接地压力呈连续分布，而在坚实地面条件下，呈非连续分布。

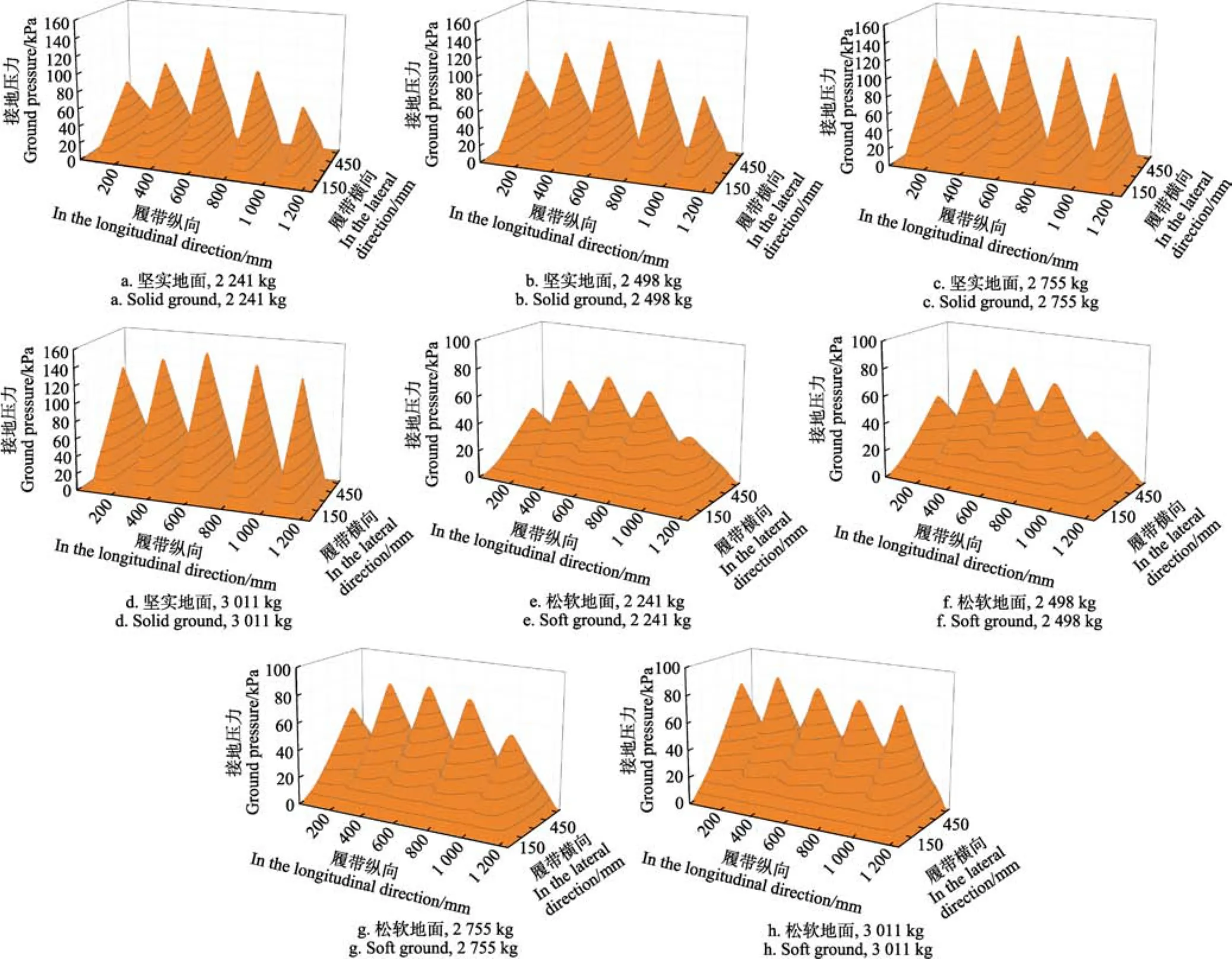
图3 不同载荷时橡胶履带轮在坚实地面和松软地面的接地压力分布Fig.3 Ground pressure distribution of rubber tracked assembly on solid ground and soft ground under different loads

图4 橡胶履带轮纵向中部的接地压力分布Fig.4 Ground pressure distribution at the centre line of rubber tracked assembly in the longitudinal direction

橡胶履带轮在不同地面的接地压力分布存在差异，主要因为地面硬度不同导致地面变形的程度不同。当地面硬度足够大时（即本文所测试的坚实地面），负重轮之间的部分履带不承担载荷，纵向上出现接地压力为 0的部分。由此可以推测另一个极端情况，当地面硬度足够小时，履带全部接地段共同承担载荷，纵向上的接地压力为平滑曲线，不存在波峰波谷。

因此，在橡胶履带轮整体结构一定的情况下，其接地压力分布主要取决于地面条件，而不同的地面条件可以近似由一个地面硬度参数进行表征。

3 橡胶履带轮接地压力数学模型

3.1 纵向上履带中部接地压力数学模型

以载荷2 241 kg时橡胶履带轮在松软地面测得的接地压力为例，为便于分析计算，取第一行负重轮接地点连线中点为原点o，履带横向为x轴，履带纵向为y轴，建立纵向上履带中部接地压力坐标系和横向上履带接地压力坐标系，如图5所示。

作出如下假设：1）单个负重轮在纵向上的接地压力曲线为二次余弦函数；2）波峰连线m(y)和波谷连线n(y)均为二次函数，其中波峰连线表达式m(y)为

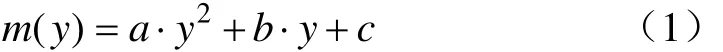
令β使n(y)=β·m(y)[7]。β取值范围为[0,1]，从接地压力曲线上看，其主要反映波峰和波谷差异大小，实质意义在于表征地面硬度。地面越松软，其取值越大，反之，取值越小。

如图5a所示，设中间接地压力峰值为σm，两端接地压力峰值为 σ1，存在 α 使得 σ1=α·σm。α 取值范围为[0,1]，表征纵向上各负重轮接地压力分配情况[16]，当中间峰值和两端峰值差异越大时，取值越小，反之，取值越大。

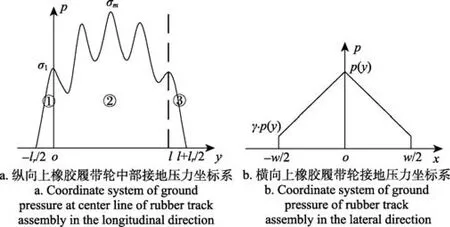
图5 橡胶履带轮接地压力坐标系Fig.5 Coordinate system of rubber tracked assembly ground pressure

分析履带中部的接地压力曲线，将其分为3段表示。

第①部分的接地压力曲线为线性函数，其表达式为

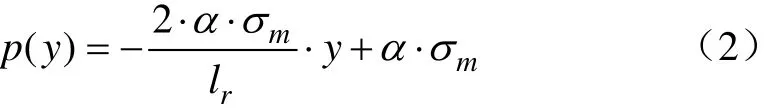
第②部分的接地压力曲线为二次余弦函数，且周期数与负重轮数相同，其表达式为

式中N为负重轮数量。m(y)和n(y)表达式为

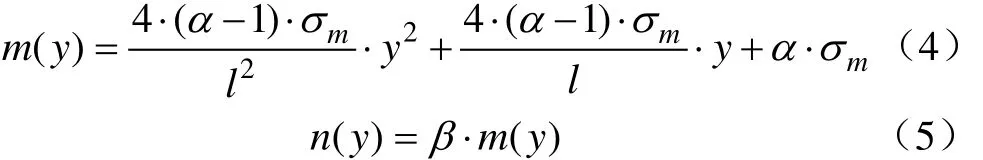
第③部分类似于第①部分，接地压力为线性函数，其表达式为

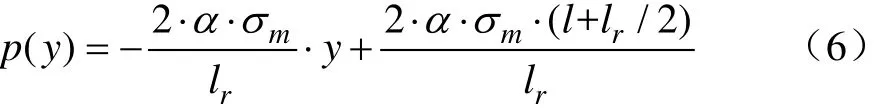
综上所述，纵向上履带中部接地压力表达式为

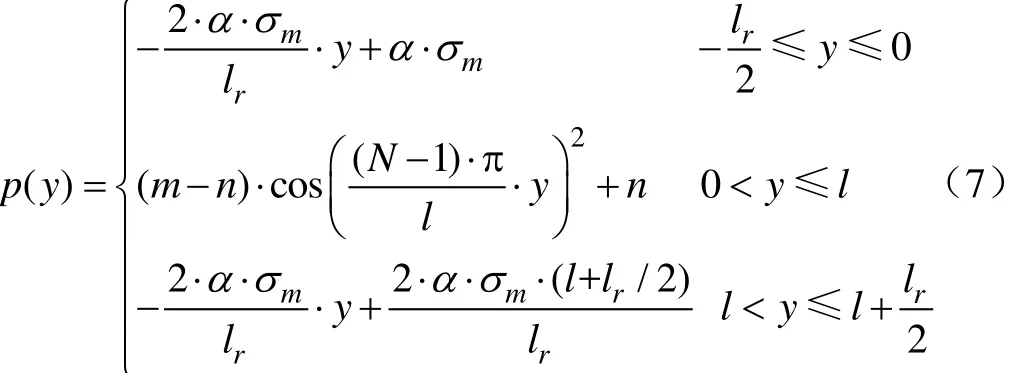
3.2 横向上橡胶履带轮接地压力数学模型

橡胶履带轮在横向上的接地压力分布可以采用线性方程表示，如图 5b所示。p(y)为履带中部接地压力，由式（7）确定。γ表征横向上各负重轮接地压力分配情况，结合试验数据和参考文献[6]，本文取γ=1/3。

综上所述，横向上橡胶履带轮接地压力表达式如下：

联立式（7）和式（8）即可得到橡胶履带轮接地压力数学模型。

3.3 模型参数确定

目前常用于表征地面硬度的参数主要包括土壤变形模量k和土壤坚固系数δ。Bekker在大量试验基础上，根据变形模量k将土壤进行分类，并给出了其参考经验值[19]。俄罗斯学者则根据坚固系数δ对土壤进行分类[20]，如表1所示。

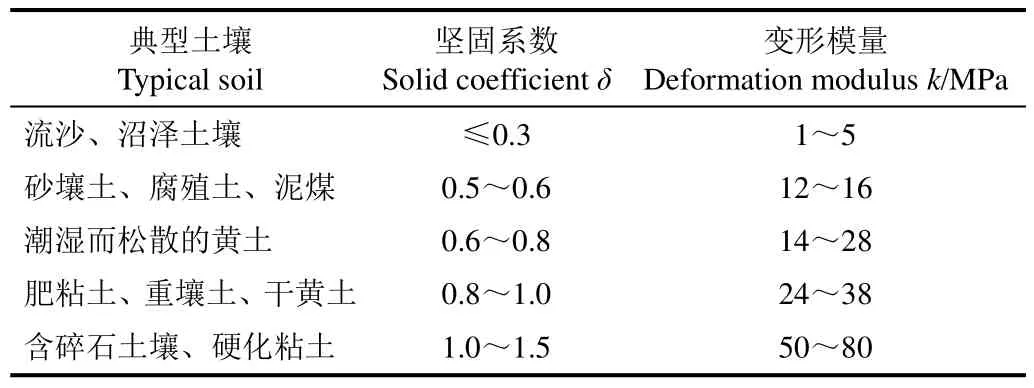
表1 典型土壤坚固系数和变形模量Table 1 Solid coefficient and deformation modulus of soil

本文提出的模型中采用β作为表征地面硬度的参数，其取值范围为[0,1]，与土壤坚固系数δ范围相近，且地面越坚实，β取值越小，对应的δ取值越大。因此，β值参照表 1中的土壤坚固程度进行选取。本文测试选取的坚实地面为在混凝土地面上铺垫一层厚钢板，硬度远大于土壤，取βH=0；松软地面为松散的砂壤土，对δ取值进行归一化处理，参照表1归一化处理结果，取βS=0.65。根据该橡胶履带轮结构参数和经验公式[6-7]，整理得式（7）和（8），涉及参数如表2所示。

表2 模型参数Table 2 Model parameters

由表 2可知，为计算橡胶履带轮接地压力，还需确定 α和 σm的值。一般情况下认为中间接地压力峰值 σm是名义接地压力σmean的2～4倍[6,21]，σmean=F/A，F为载荷大小，A为接地面积。

右前轮载荷为2 241、2 498、2 755、3 011 kg时，其名义接地压力为 30.50、34.00、37.50、40.98 kPa，在坚实地面的接地压力峰值分别为126.77、135.45、145.44、153.30 kPa，在松软地面的接地压力峰值分别为 73.93、77.63、82.36、91.16 kPa。分析数据可知，在坚实地面条件下 σm≈2.29σmean，在松软地面条件下 σm≈3.88σmean。

确定除 α以外的参数后，对橡胶履带轮接地压力表达式进行迭代计算。根据所需精度要求，将α依次取0～1，由仿真结果反推橡胶履带轮载荷 Fsim，即 Fsim=∫p(x,y)dxdy，使|(Fsim–F)/F取得最小值的α即为所求值。最终计算得载荷为2 241、2 498、2 755、3 011 kg时，在坚实地面α分别为0.71、0.74、0.75、0.80；在松软地面α分别为0.75、0.77、0.80、0.84。

3.4 仿真结果与试验数据对比

基于模型仿真橡胶履带轮在坚实地面和松软地面的接地压力分布，并将履带中部接地压力的仿真结果与测试数据进行对比，如图6所示。

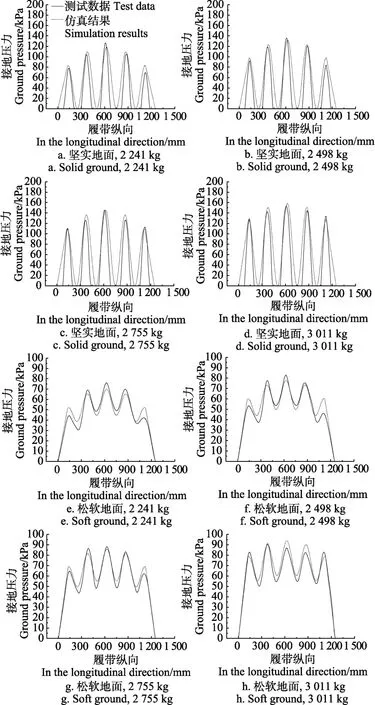
图6 橡胶履带中部接地压力的测试数据与仿真结果Fig.6 Test data and simulation results of ground pressure at the centre line of rubber tracked assembly

分析图 6可知，在坚实地面条件下，模型能够较好地预测负重轮下的接地压力峰值，以及橡胶履带轮中部和两端接地压力的分配关系。但模型不能很好地反映出负重轮间履带的接地压力情况，4种试验条件下的最大仿真误差约为8.56%。

在松软地面条件下，模型能够较好地预测各负重轮下的接地压力峰值及橡胶履带轮接地压力分布情况，但当载荷较小时，模型不能很好地反映出橡胶履带轮中部和两端接地压力的分配关系。4种试验条件下的最大误差约为6.40%。

4 基于模型静态转向阻力矩分析与验证

为考察本文提出的橡胶履带轮接地压力数学模型在进行性能分析的适用性和准确性，应用该模型推导计算橡胶履带轮在坚实地面和松软地面条件下的静态转向阻力矩，并进行试验验证。

4.1 坚实地面条件下的静态转向阻力矩

区别于整体式履带车辆，橡胶履带轮的转向中心位于履带内侧[22-23]。为便于计算分析，以转向节的转向主销在地面上的投影O为坐标原点（即履带速度瞬心），履带横向为X轴，履带纵向为Y轴，建立静态转向阻力矩坐标系，如图7所示。

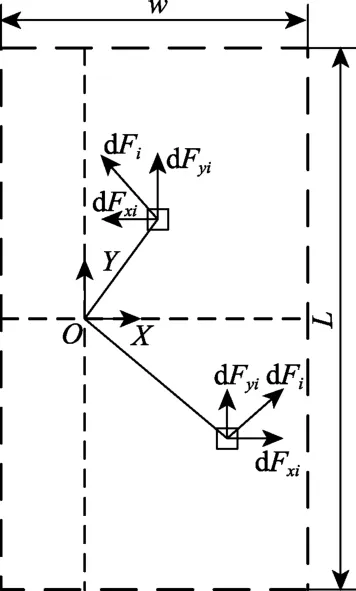
图7 静态转向阻力矩坐标系Fig.7 Coordinate system of static steering resistance moment

由于速度瞬心履带内侧，转向时橡胶履带接地段某一微元发生的运动是橡胶履带轮绕速瞬心产生沿 X方向的横向位移dx和沿Y方向的纵向位移dy，其所受到的作用力分别为横向反力dFxi和纵向反力dFyi。设该微元接地压力为p(x,y)，则其摩擦力dFi表达式为式中转向阻力系数μt=0.9[24]。

根据静态转向阻力矩计算坐标系，对推导的橡胶履带轮接地压力数学模型进行坐标变换，从而得到该坐标系下对应的p(x,y)。因此，橡胶履带轮在坚实地面条件下的静态转向阻力矩表达式为

应用Matlab软件对式（10）进行计算，即得到不同载荷时坚实地面条件下的静态转向阻力矩，如表3所示。

4.2 松软地面条件下的静态转向阻力矩

橡胶履带轮在松软地面条件下的静态转向阻力矩服从Mohr-Coulomb理论[25]。设某一微元接地压力为p(x,y)，则其摩擦力dFi表达式为

式中c为土壤内聚系数，kPa；φ为内摩擦角, (°)。

类比坚实地面条件下静态转向阻力矩的推导过程，橡胶履带轮在松软地面条件下的静态转向阻力矩表达式为

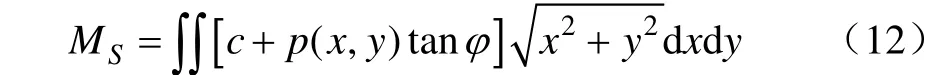
采用北京航空航天大学研发的一种土壤承压和剪切特性测试仪[26-27]，对试验地面进行了土壤力学特性试验，得到土壤参数c=4.27 kPa和φ=22°。

将各参数代入式（12）中，应用Matlab软件进行计算，得到不同载荷时松软地面条件下的静态转向阻力矩，如表3所示。

4.3 试验验证

对橡胶履带轮的转向杆件进行应力应变测试，得到其静态转向阻力矩。试验时，首先连接动态数据采集系统和PC机，并在转向横拉杆上贴45°应变花，如图8所示。然后分别在坚实地面和松软地面上，当右前轮载荷为2 241、2 498、2 755、3 011 kg时转动方向盘，通过动态数据采集系统得到转向初始状态时转向杆应变，每种条件下进行 3次试验，取平均值。将测得的应变换算为主应力，再乘以连杆截面积得到横拉杆轴向拉压力，最后乘以力臂即可得到橡胶履带轮的静态转向阻力矩。

图8 静态转向阻力矩测试现场Fig.8 Test site of static steering resistance moment

测得坚实地面和松软地面上不同载荷时橡胶履带静态转向阻力矩如表 3所示。可以看出，仿真结果与试验数据存在一定误差，其主要原因在于接地压力模型与实际接地压力分布仍存在一定误差。仿真结果与试验数据的最大误差为4.71%，在可接受范围内。因此，本文提出的橡胶履带轮接地压力模型能够在一定误差范围内较好地适用于对橡胶履带轮静态转向阻力矩的分析。

表3 静态转向阻力矩的仿真结果与试验数据Table 3 Simulation results and test data of static steering resistance moments

5 结 论

本文以课题组自主研发的SDL01橡胶履带轮为研究对象，分别在坚实地面和松软地面条件下测量了橡胶履带轮的接地压力，其分布具有以下规律：1）在履带长度方向上，接地压力呈多峰值非均匀分布，且峰值呈钟罩型分布，载荷越大，各峰值分布越均匀；在履带宽度方向上，接地压力呈钟罩型连续分布。2）在坚实地面条件下，负重轮间履带几乎不承重，接地压力呈非连续分布；在松软地面条件下，橡胶履带整体承重，接地压力呈连续分布。

根据橡胶履带轮接地压力分布规律，本文提出了一种接地压力分布数学模型，纵向上的接地压力分布采用二次余弦函数表示，横向上的接地压力分布采用线性函数表示。模型中采用地面硬度参数表征不同的地面条件，避免了进行土壤承压和剪切试验，提高了模型的实用性。但该模型不能很好地反映出在坚实地面条件下负重轮间履带不承重的现象，仍有待进一步优化。

基于该模型，对橡胶履带轮静态阻力矩进行了计算分析和试验验证。结果表明，模型仿真结果与试验数据的最大误差为4.71%，因此，该接地压力模型能够在一定误差范围内适用于对橡胶履带轮静态转向阻力矩的分析。本文提出的模型也可用于橡胶履带轮的结构设计和其他性能研究。

[1] 郭浩亮，穆希辉，杨小勇，等. 四橡胶履带轮式车辆转向力学性能分析与试验[J]. 农业工程学报，2016，32(21)：79－86.Guo Haoliang, Mu Xihui, Yang Xiaoyong, et al. Mechanics properties analysis and test of four rubber tracked assembly vehicle steering system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(21): 79－86. (in Chinese with English abstract)

[2] 吕凯，穆希辉，郭浩亮，等. 橡胶履带轮履带周长建模与试验[J]. 农业机械学报，2016，47(11)：329－340.Lv Kai, Mu Xihui, Guo Haoliang, et al. Model and test of the track perimeter of conversion rubber track assembly[J].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(11): 329－340. (in Chinese with English abstract)

[3] Garber M, Wong J Y. Prediction of ground pressure distribution under tracked vehicles—I. An analytical method for predicting ground pressure distribution[J]. Journal of Terramechanics, 1981, 18(1): 1－23.

[4] Okello J A, Watany M, Crolla D A. A theoretical and experimental investigation of rubber track performance models[J]. Journal of Agricultural Engineering Research,1998, 69(1): 15－24.

[5] Arvidsson J, Westlin H, Keller T, et al. Rubber track systems for conventional tractors - Effects on soil compaction and traction[J]. Soil & Tillage Research, 2011, 117(6): 103－109.

[6] Keller T, Arvidsson J. A model for prediction of vertical stress distributionnear the soil surface below rubber-tracked undercarriage systems fitted onagricultural vehicles[J]. Soil& Tillage Research, 2016, 155: 116－123.

[7] 陈秉聪，范雅操，任露泉. 接地压力动态变化下履带推力与土壤参数间关系的研究[J]. 吉林工业大学学报，1984(1)：67－84.Chen Bingcong, Fan Yacao, Ren Luquan. Study on relationship between track thrust and soil parameters under dynamic change of ground pressure[J]. Journal of Jilin University of Technology, 1984(1): 67－84. (in Chinese with English abstract)

[8] 杨士敏. 履带车辆接地比压分布规律对附着力的影响[J].中国公路学报，1995，8(2)：85－88.Yang Shimin. The effects of tracked vehicles contact pressure distribution on adhesive force[J]. China Journal of Highway and Transport, 1995, 8(2): 85－88. (in Chinese with English abstract)

[9] 许焰，吴鸿云，左立标. 履齿高度对集矿机牵引性能的影响及参数确定[J]. 农业工程学报，2012，28(11)：68－74.Xu Yan, Wu Hongyun, Zuo Libiao. Influence of shoe tooth height of tracked vehicle on traction performance and its parameter determination[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(11): 68－74. (in Chinese with English abstract)

[10] 栗浩展，王红岩，芮强，等. 履带车辆地面牵引力的计算与试验验证[J]. 装甲兵工程学院学报，2015，29(1)：36－40, 105.Li Haozhan, Wang Hongyan, Rui Qiang, et al. Calculation and testing verification of ground traction of tracked vehicles[J]. Journal of Academy of Armored Force Engineering, 2015, 29(1): 36－40, 105. (in Chinese with English abstract)

[11] 王红岩，陈冰，芮强，等. 集中载荷作用下的履带车辆稳态转向分析与试验[J]. 兵工学报，2016，37(12)：2196－2204.Wang Hongyan, Chen Bing, Rui Qiang, et al. Analysis and experiment of steady-state steering of tracked vehicle under concentrated load[J]. Acta ArmamentarII, 2016, 37(12): 2196－2204. (in Chinese with English abstract)

[12] 王红岩，王钦龙，芮强，等. 高速履带车辆转向过程分析与试验验证[J]. 机械工程学报，2014，50(16)：162－172.Wang Hongyan, Wang Qinlong, Rui Qiang, et al. Analyzing and testing verification the performance about high-speed tracked vehicles in steering process[J]. Journal of mechanical engineering, 2014, 50(16): 162－172. (in Chinese with English abstract)

[13] Tang S X, Yuan S H, Hu J B, et al. Modeling of steady-state performance of skid-steering for high-speed tracked vehicles[J]. Journal of Terramechanics, 2017, 73: 25－35.

[14] 吕凯. 重载可更换式橡胶履带轮设计及理论研究[D]. 石家庄：军械工程学院，2014.Lv Kai. Research of Design and Theory of Heavy-Duty Conversion Rubber Track Assembly[D]. Shijiazhuang:Ordnance Engineering College, 2014. (in Chinese with English abstract)

[15] 黄舸舸，张甲，向宗义，等. 利用 Tekscan 压力分布测量系统进行轮胎接地分析[J]. 轮胎工业，2008，28(9)：563－565.Huang Gege, Zhang Jia, Xiang Zongyi, et al. Analysis of tire ground pressure using tekscan pressure distribution measurement system[J]. Tire Industry, 2008, 28(9): 563－565. (in Chinese with English abstract)

[16] Keller T. A model for prediction of the contact area and the distribution of vertical stress below agricultural tyres from readily-available tyre parameters[J]. Biosystems Engineering,2005, 92(1): 85－96.

[17] Schjønning P, Lamandé M, Tøgersen F A, et al. Modelling effects of tyre inflation pressure on the stress distribution near the soil-tyre interface[J]. Biosystems Engineering, 2008(99):119－133.

[18] 陈泽宇，郭秀红，张承宁. 接地长宽比的设计对履带车辆行驶性能的影响[J]. 农机化研究，2010(5)：112－114.Chen Zeyu, Guo Xiuhong, Zhang Chengning. Effects of L/B value to tracked vehicles steering characteristic[J]. Journal of Agricultural Mechanization Research, 2010(5): 112－114. (in Chinese with English abstract)

[19] Bekker. Theory of Land Locomotion[M]. Michigan: The University of Michigan Press, 1956.

[20] Clark S J. A proposed soil classification systems for soil-vehicle and tillage mechanics[J]. Journal of Terramechanics, 1973, 10(3): 9－19.

[21] Bekker. Introduction to terrain-vehicle Systems[M].Michigan: The University of Michigan Press, 1969.

[22] 芮强，王红岩，王钦龙，等. 基于剪应力模型的履带车辆转向力矩分析与试验[J]. 兵工学报，2015，36(6)：968－977.Rui Qiang, Wang Hongyan, Wang Qinlong, et al. Analysis and experiment of tracked vehicle steering torque based on shear stress model[J]. Acta ArmamentarII, 2015, 36(6): 968－977. (in Chinese with English abstract)

[23] 李勇，姚宗伟，王国强. 四履带车辆转向性能仿真研究[J].农业机械学报，2011，42(2)：34－38，47.Li Yong, Yao Zongwei, Wang Guoqiang. Steering performance simulation of four‒tracked vehicle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011,42(2): 34－38, 47. (in Chinese with English abstract)

[24] Wong J Y. Theory of Ground Vehicle, 4rd Edition[M].Hoboken, New Jersey: John Wiley and Sons Incorporation,2008.

[25] 郭浩亮. 三角橡胶履带轮式全地形车转向力学特性理论与试验研究[D]. 石家庄：军械工程学院，2015.Guo Haoliang. Theoretical and Experiment Research on Steering Mechanical Properties of All-terrain Loader with Triangular Rubber Track Assembly[D]. Shijiazhuang:Ordnance Engineering College, 2015. (in Chinese with English abstract)

[26] 高峰，崔莹，徐国艳，等. 一种土壤承压和剪切试验测试仪：201310028831.5[P]. 2015-11-18.

[27] 丁青. 重力场对土壤可行驶性影响的试验研究[D]. 北京：北京航空航天大学，2013.Ding Qing. Experimental Study About the Influence of Gravity on Soil's Travelability[D]. Beijing: Beihang University,2013. (in Chinese with English abstract)