最近邻移动模式下的Lanchester作战动力学研究

崔怡望，田宝国，王 栋

(海军航空工程学院 a.研究生管理大队； b.基础部， 山东 烟台 264001)

Lanchester方程于1914年被提出[1]，是描述空战的数学模型，国内外研究者在该模型基础上进行了大量研究[2-4]，研究者普遍认为Lanchester作战法则——线性律和平方律已经过时，不能用来解释说明现代战争，原因在于现代战争的进程和结果很大程度上依赖于复杂的环境、士兵能力以及战术策略等综合因素，于是有些学者在原有常微分方程的基础上进一步深入研究，引入了空间因素。Lauren等使用元胞自动机模型对Lanchester作战的时空动力学[5-13]进行了研究，他们通过建立有分形特征的作战方程解释特定环境下作战兵力采用分散式、游击战式或群集式策略的有效性。Ilachinski对早期的智能体作战模型进行了研究[14-16]，随着21世纪的到来，无人机、机器人以及网络通讯技术、传感器的迅速推广和使用，智能体模型在经济、社会、军事等领域的研究呈爆发式发展[17-22]，并具有巨大的应用价值与发展前景。Protopopescu等人解决了军队通过战斗空间的运动模拟问题[23-24]，将Lanchester常微分方程形式扩展到了偏微分方程形式，对部队行进过程中的扩散效应和作战双方之间不同的相互作用等造成的影响进行了研究。后来Gonzalez、Spradlin、Keane等人用偏微分方程分别研究了作战双方在整个战斗区域里的运动或者扩散效应以及更为复杂的时空演化动力学[25-32]，已成为Lanchester作战模型研究的新发展方向。

已有研究中的Lanchester作战模型都没有考虑作战个体的移动模式，为了能更好地解释上述问题，本文运用随机点阵模拟方法，研究了最近邻移动模式下的Lanchester作战时空动力学。

1 模型

首先建立模型，模拟环境为规模100×100的平面网格，采用周期边界条件。二维平面网格上中的每一个位置由红、蓝双方个体A、B占有，规定每一位置最多有一个个体，若某位置上没有红、蓝个体，则用空位置φ表示。作战双方个体A、B以及空位置φ之间的关系如下：

(1)

(2)

式(1)、式(2)中：e为交换速率，表示双方个体的宏观流动性；μ为消灭增援速率，体现的是双方个体的战斗力与增援能力。为简明起见，规定所有作战个体的移动模式均为最近邻移动模式，此模式指的是作战个体每次仅能移动到与其最近邻的空间位置，如在本文工作中，每个个体每次仅能移动到与其最近邻的上、下、左、右4个空位置处；进一步假定所有作战个体使用武器的平均有效杀伤范围也是最近邻模式，例如使用某种轻武器的步兵大致具有这两个特点。

上述模型所描述的是平面网格上大量个体按照式(1)、式(2)发生相互作用的随机过程，根据Durrett[33]、Reichenbach[34]等学者运用随机模拟方法对平面网格上随机的循环博弈过程等所进行的卓有成效研究，本文采用相同的随机模拟方法进行Monte Carlo模拟，具体步骤为：首先随机选择某一个位置的个体，再从其上、下、左、右最近邻4个位置处的个体中随机选择一个，随之发生式(1)、式(2)所表示的相互作用。红、蓝个体间的相互作用行为如图1 (a)～图1(e)所示。

图1 红、蓝方相互作用行为示意图

2 随机模拟

2.1 消灭增援率——交换率临界曲线

在随机点阵模拟过程中，红方A、蓝方B与空位置φ的初始分布比例大致为3∶3∶4，且为均匀随机分布。消灭增援率μ和交换率e为可调参量。调整交换率和消灭增援率等参量，观察红、蓝双方的动态战斗与斑图演化过程。在随机点阵模拟过程中，当模拟代数等于10 000时，若红、蓝双方均存在，定义为稳定共存状态；若红、蓝双方中的其中一方被消灭，定义为非稳定共存状态。

调整消灭增援速率μ、交换速率e的值，分别进行随机模拟，通过模拟得到稳定共存与非稳定共存的临界曲线，如图2所示，两临界曲线及其中间所夹区域为红、蓝双方非稳定共存的参量区域，其他参量区域对应于红、蓝双方稳定共存状态。

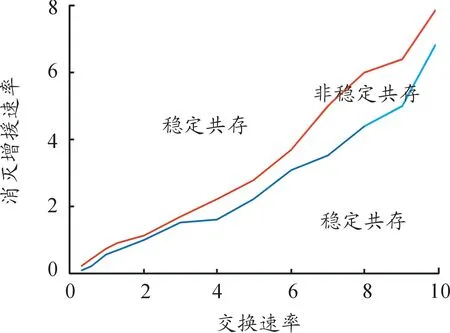
图2 最近邻移动模式下的消灭增援率——交换率临界曲线

2.2 消灭增援速率自左向右呈梯度变化

图3(a)～图3(d)分别为消灭增援速率呈梯度变化时，随机点阵模拟到5 000代、7 000代、9 000代、11 000代时的斑图。

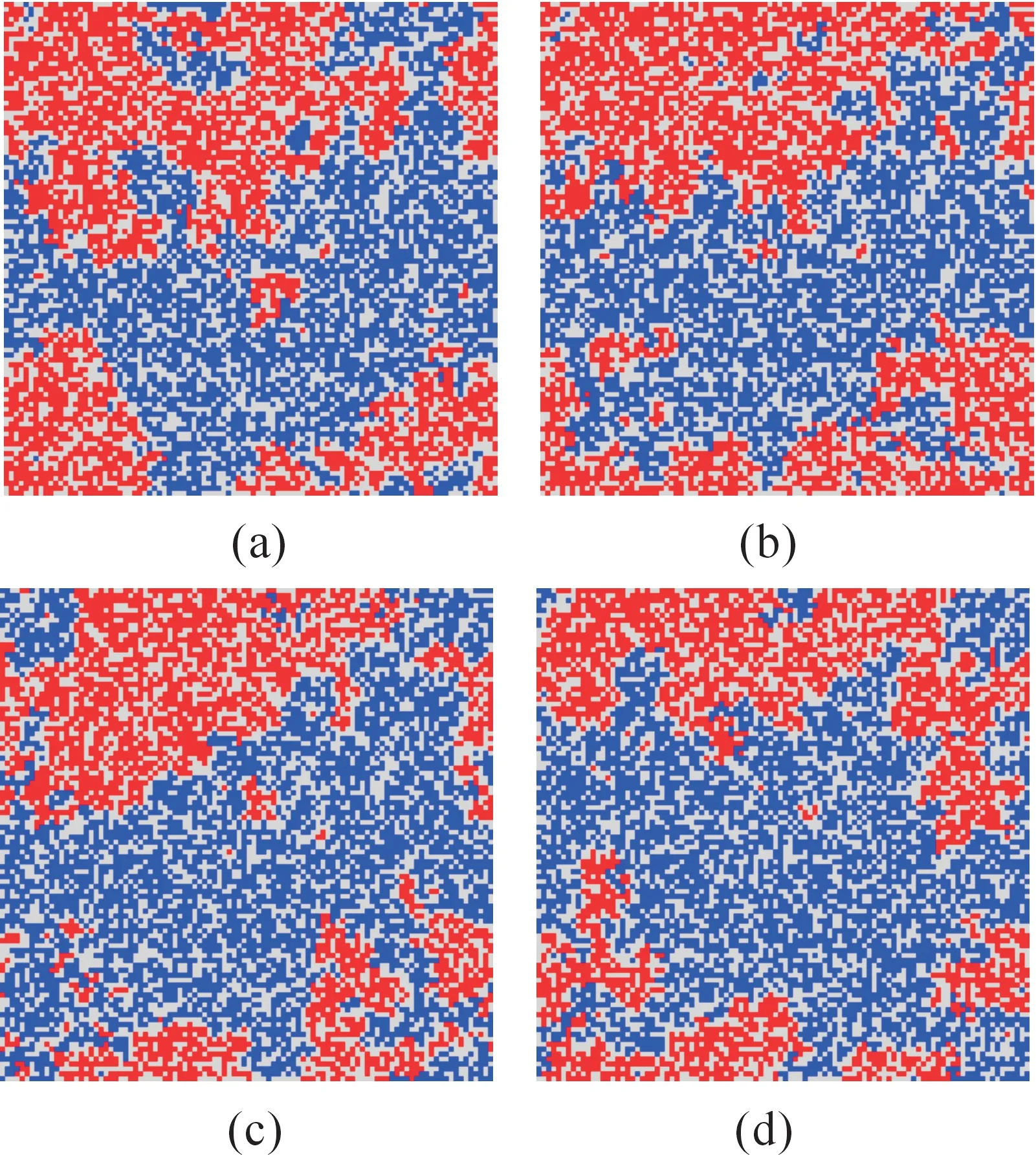
图3 消灭增援速率呈梯度变化时的斑图

然后，改变消灭增援速率为无梯度变化，其他条件保持不变，选取随机模拟到相同代数下的斑图与之进行对比。相同条件下，消灭增援速率无梯度变化时斑图演化如下：

观察图3和图4，对比消灭增援速率有无梯度变化时的斑图演化过程，发现：交换速率等参数均相同的条件下，当消灭增援速率呈梯度变化情况时，二维网格中右边位置的个体更容易消灭其左边位置的个体，特别是在形成稳定的斑图之后，观察效果更加明显，斑图中呈现右边斑块逐渐吞蚀左边斑块的趋势，即右边斑块呈逐渐向左扩散趋势；而当消灭增援速率无梯度变化时，斑块有扩散现象，但其扩散方向无明显趋势，没有发现上述规律。

分析造成上述现象的原因：消灭增援速率呈梯度变化时，二维网格自左向右消灭增援速率逐渐增大，而消灭增援速率代表个体间战斗力的强弱，当左、右两个体相遇时，右边个体战斗力更强，更易消灭左边个体，所以当形成稳定斑块之后，右边斑块更易消灭左边斑块，相反，左边斑块更易被吞蚀，斑块整体上呈向左扩散趋势；而当消灭增援速率无梯度变化时，二维网格中每个位置上的消灭增援速率是相等的，即每个个体战斗力相同，消灭对方的概率也相同，所以，当斑图形成稳定斑块之后，每个斑块向上、下、左、右4个方向扩散的概率是均等的，扩散方向无明显趋势。

对应上述斑图中参数，随机点阵模拟每隔100代计算一次双方密度，统计前50 000代内双方密度，得到消灭增援速率有无梯度变化情况下的双方密度时间序列曲线如图5、图6所示。

图4 消灭增援速率无梯度变化时的斑图

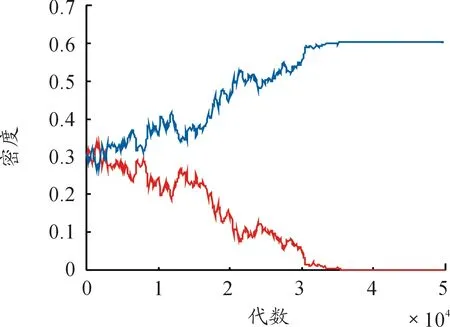
图5 消灭增援速率呈梯度变化时密度时间曲线

图6 消灭增援速率无梯度变化时密度时间曲线

观察图5和图6，两种情况下双方均能保持稳定共存状态，但稳定共存代数有差别，发现消灭增援速率呈梯度变化时，双方稳定共存时间较短。为了排除实验的随机性，两种情况对应参数下，各随机模拟100次，记录双方稳定共存代数，并取平均值，得到结果：消灭增援速率无梯度变化情况下，当其值取最小基础值μ=1，交换速率取e=0.000 1时，稳定共存代数为60 698代；当其值取其梯度变化过程中的最大值μ=2时，稳定共存代数为54 341代。而当消灭增援速率呈梯度变化时，稳定共存代数为73 766代。对结果进行分析，消灭增援速率呈梯度变化时反而影响了双方个体间的相互作用，延长了双方共存时间，呈梯度变化造成双方稳定共存时间更长。

2.3 交换速率自左向右呈梯度变化

图7(a)～图7(d)分别是交换速率呈梯度变化时，随机点阵模拟到24 010代、24 020代、24 030代、24 040代的斑图。

图7 交换速率呈梯度变化时的斑图

然后，改变交换速率为无梯度变化，其他条件保持不变(μ=1、e=0.01)，选取随机模拟到相同代数下的斑图与之进行对比。相同条件下，交换速率无梯度变化时斑图演化如下：

随机模拟过程中，选取模拟代数间隔为10代，主要是考虑到交换速率对双方个体的流动性影响较大，不同交换速率情况下，斑图变化较快，如果模拟代数间隔较大，不易观察到斑图的细微变化，遂将随机模拟代数间隔取为10代。观察图7和图8，对比消灭增援速率有无梯度变化时的斑图演化过程，发现：当交换速率呈梯度变化时，红、蓝作战双方发生相互作用并形成稳定斑块之后，红、蓝交界处发生相互扩散现象，造成红、蓝斑块交界处零散混乱，小斑点较多，斑块边缘模糊；而当交换速率无梯度变化时，稳定斑块形成后，红、蓝边界清晰、整齐，无斑点散乱现象出现。

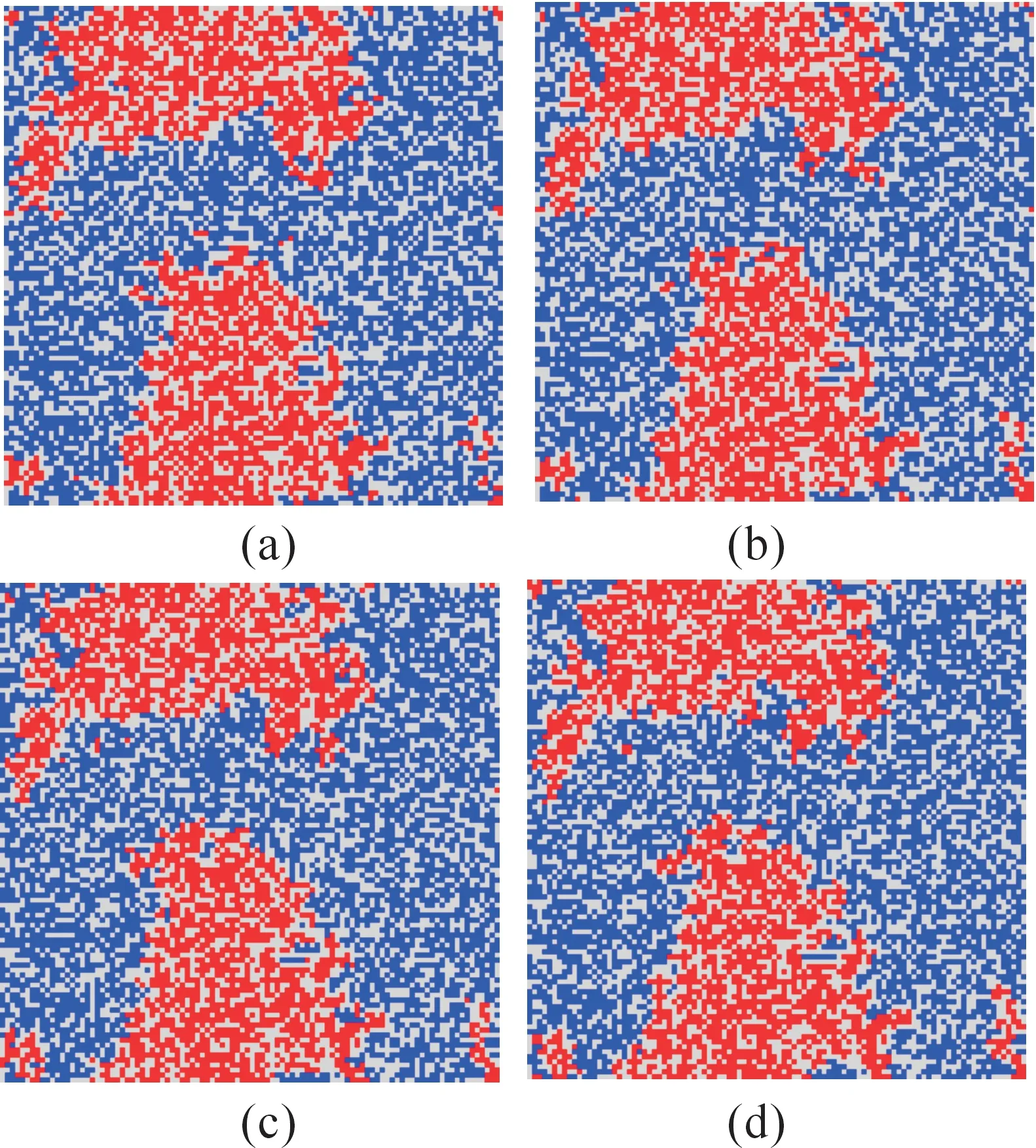
图8 交换速率无梯度变化时密度时间曲线

分析造成上述现象的原因：当交换速率呈梯度变化时，二维平面网格中，按照位置自左向右交换速率依次增大，造成的结果是右边个体流动性较强，虽然斑块内部个体发生移动对斑块影响不明显，斑块内部观察不到明显变化，但是斑块边界处即红蓝斑块交界处右边红方或者是蓝方个体更易与左边的空格发生交换，同理，右边的空格也会与左边红方或蓝方个体发生交换，从而导致双方个体扩散到敌方斑块当中，由于双方个体消灭增援速率相同，各个位置上的消灭增援速率也相同，当斑点扩散到斑块当中后，被周围敌方消灭或者扩散侵蚀敌方个体形成较大斑块，最终导致的结果就是红蓝斑块边界模糊，交界处斑点混乱；当交换速率无梯度变化时，二维网格中各个位置交换速率相同，边界处界线明显，无散乱斑点出现。

在随机点阵模拟过程中，还发现：交换速率呈梯度变化时，基本上不能形成较大的稳定斑块，即使形成，也会很快被敌方个体的扩散破坏，从而变为较为松散零碎的小斑块，红、蓝双方个体分布较为混乱。分析其原因：各个位置交换速率的不同造成对斑图的整体流动性影响较大，从而造成斑图不稳定，极易改变。

对应上面斑图中的参量，随机点阵模拟每隔100代计算一次双方密度，统计前50 000代双方密度，得到交换速率有无梯度变化情况下，双方密度时间序列曲线如图9、图10所示。

图9 交换速率呈梯度变化时密度时间曲线

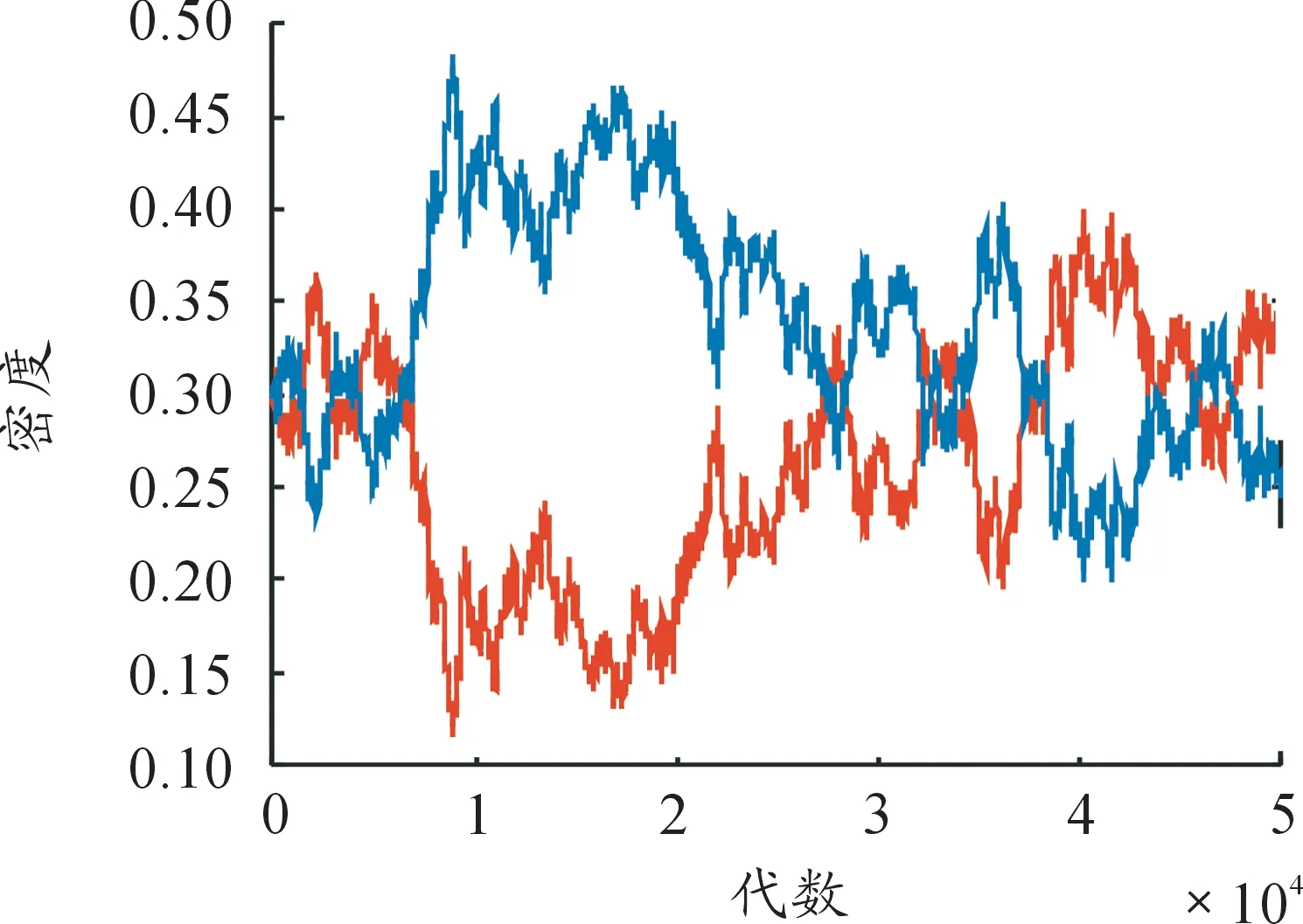
图10 交换速率无梯度变化时密度时间曲线

3 战术组合

考虑到人为因素的影响，对最近邻移动模式下，红、蓝双方有战术组合“二对一”，均无战术组合以及仅一方有战术组合“二对一”3种情况进行了研究。

3.1 红、蓝双方均有战术组合

红、蓝双方均有战术组合的情况：红、蓝双方个体A、B和空格φ之间的关系如下：

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

式(3)、式(4)是“一对一”的情况，红、蓝个体的消灭增援速率均为k1，交换速率为e；式(5)、式(6)、式(7)是两个红方个体对一个蓝方个体的情况，蓝方个体被消灭，且在原蓝方个体位置增援一个红方个体的速率为k2，两个红方个体中有一个个体被消灭，且在被消灭红方个体位置增援一个蓝方个体的速率为k3，两个红方个体均被消灭，且在被消灭位置上增援两个蓝方个体的速率为k4，同理，式(8)、式(9)、式(10)是两个蓝方个体对一个红方个体的情况。

随机点阵模拟过程中，对应各个参量值为：k1=e=1，k2=k5=2.2，k3=k6=0.4，k4=k7=0.2，模拟过程中选取如下斑图进行观察和分析。

图11(a)和图11(b)分别为双方均有战术组合情况下，随机点阵模拟到10 500代、17 500代时所得斑图，观察整个斑图演化过程，发现：斑图中斑块形成速度较快，当模拟到500代时已经形成了较为稳定的大斑块，且红、蓝斑块中间分界线清晰，无混乱小斑点，随机点阵模拟到4 000代时，整个斑图分为红、蓝两个大斑块，红、蓝双方个体完全分离，整个模拟过程中，斑图在形成稳定斑块后，随时间整体上变化较慢，蓝方个体通过红、蓝斑块的分界线缓慢向红方斑块扩散，造成蓝方数量逐渐增加，红方数量逐渐减小，蓝方斑块吞蚀红方斑块的过程中，红、蓝斑块边界明显，无混乱小斑点出现。

图11 双方均有战术组合时的斑图

相同参数下，重复模拟多次，发现红、蓝胜负各半，斑图演化过程规律相同，结论一致。模拟过程中统计前100 000代内双方的密度，得到双方密度时间序列曲线如图12。

然后，保持k1、e、k3、k4、k6、k7的取值不变，增大k2、k5的值，依然保持k2=k5，调整k2=k5=3，单独研究参数k2、k5对斑图演化的影响，模拟过程中选取如下斑图进行分析。

图12中，(1)和(2)分别是当k2=k5=3时，随机点阵模拟到4 000代、11 000代时所得的斑图，斑图中斑块规模对应的是双方数量，(3)和(4)代数间隔为7 000代，红、蓝斑块大小变化大，而图11中，(1)和(2)代数间隔同样为7 000代，红、蓝斑块大小变化并不明显，双方数量变化小，说明当稳定斑图形成后，k2、k5的值越大，相同时间内斑图中的斑块变化越大，即双方数量随时间变化越快，从而造成双方稳定共存时间越来越短。图14对应上面斑图参数下的双方密度时间序列曲线，与图12相比，明显观察到双方稳定共存时间缩短。改变对应参数的取值，对多组不同参数情况进行相同操作，随机模拟结果均与上述结论一致。

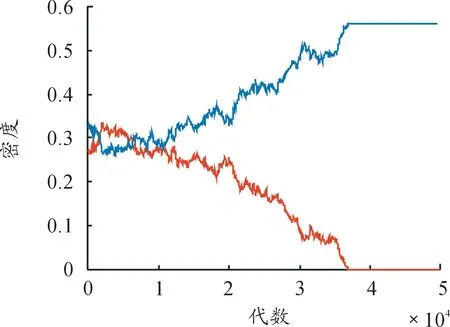
图12 双方均有战术组合时的密度时间序列曲线

图13 双方均有战术组合时的斑图(k2=k5=3)

图14 双方均有战术组合时的密度时间序列曲线(k2=k5=3)

调整参数，对不同参数下的各种情况进行随机模拟，分别单独研究了参数k3、k6和k4、k7对斑图演化的影响，总结如下：保持k1、e、k2、k5的取值不变，分别单独增大k3、k6和k4、k7的值，但依然保持k3=k6，k4=k7，发现k3、k6和k4、k7值的增大会改变斑图中斑块的形状和规模大小，影响双方稳定共存时间；其值越大，稳定共存时间越长。

3.2 红、蓝双方均无战术组合

为了与有战术组合情况形成对比，令消灭增援速率为μ=1，交换速率为e=1，选取相同参数下无战术组合时的斑图如下：

图15(a)和图15(b)分别为双方均无战术组合情况下，随机点阵模拟到500代、1 000代时所得斑图，通过观察斑图演化过程，与有战术组合情况相比：当模拟到500代时，虽然斑图中斑块已经形成，但极不稳定，随时间变化大，间隔500代，当模拟到1 000代时，斑图又变为另外一种情况，且红、蓝斑块分界处小斑点较多，斑图整体上较为混乱，且红、蓝双方个体扩散方向不固定，向各个方向均有扩散，大斑块中夹杂着敌方小斑点，与相同参数下的有战术组合情况下的斑图相比，整个斑图中斑块不集中；而有战术组合时，整个斑图分为红、蓝两个大斑块，红、蓝双方个体完全分离，整个模拟过程中，斑图在形成稳定斑块后，随时间整体上变化较慢，蓝方个体通过红、蓝斑块的分界线缓慢向红方斑块扩散，造成蓝方数量逐渐增加，红方数量逐渐减小。相同参数下，重复模拟多次，发现红、蓝胜负各半，斑图演化过程规律相同，结论一致，双方密度时间序列曲线如图15、图16。

图15 双方无战术组合时的斑图

观察图15和图16，双方个体有无战术组合这两种情况下，双方均能保持稳定共存状态，但稳定共存代数有所差异，对有无战术组合两种情况进行随机模拟100次，得到结果：有战术组合时，双方稳定共存代数为46388代；无战术组合时，稳定共存代数为41 387代。由此可见，相同条件下，战术组合影响双方相互作用时间，战场上可以通过添加控制条件，改变战术，从而得到对自己有利的结果。

图16 双方无战术组合时的密度时间序列曲线

3.3 仅红方有战术组合

仅红方有战术组合情况下，红、蓝双方个体A、B和空格φ之间的关系仅满足式(3)、式(4)、式(5)、式(6)、式(7)，令参数k5=k6=k7=0，对应有战术组合情况下的参数，其他参数保持不变，通过观察模拟过程中的斑图演化，发现双方共存时间大约为100代左右，红方很快就将蓝方完全消灭了。具体选取如下斑图进行分析。

图17(a)和图17(b)分别是仅红方有战术组合情况下，随机点阵模拟到10代、20代时所得斑图，观察斑图发现，红、蓝双方数量变化速度快，仅仅间隔10代，红方数量剧增，蓝方数量剧减，直到蓝方被完全消灭。对应上面斑图中的参量，双方密度时间序列曲线如图18，图18中清楚地观察随机点阵模拟到100代左右，蓝方被全部消灭。随机模拟100次，得到仅红方有战术组合情况下，k5=k6=k7=0，k2=2.2，k3=0.4，k4=0.2时，双方共存代数为109代。

图17 仅红方有战术组合时的斑图

图18 仅红方有战术组合时的密度时间序列曲线

选取多组不同的参数，对各种不同情况进行随机点阵模拟，发现：当参数k5=k6=k7=0且保持不变的情况下，控制参数k2的值适当减小，k3和k4的值适当增大时，造成红方消灭蓝方的时间越长，相反，参数k2的值越大，控制k3和k4的值适当减小时，造成红方消灭蓝方的时间越短，但当参数k2的值小到一定的程度且k3和k4的值增大到一定程度后，原本“占绝对优势”的红方反而被无战术组合的蓝方消灭。

4 结论

本研究运用随机点阵模拟方法，对最近邻移动模式下的Lanchester作战模型进行了研究，得到了稳定共存与非稳定共存的参量条件与临界曲线，并研究了两个重要参量有无梯度变化情况下的斑图演化与双方密度时间序列曲线。研究发现，消灭增援速率呈梯度变化时影响双方个体间的相互作用，使得双方稳定共存时间延长，而交换速率呈梯度变化时，使总体流动性增强，整体作战效率提高，缩短了双方共存时间，促进了战斗进程。本文还研究了战术组合对双方作战的动力学影响，斑图演化过程中，双方均有战术组合情况下，双方自组织性强，易形成稳定的大斑块，相反，双方没有战术组合时，双方自组织性弱，斑图中零碎小斑块多，大斑块少，仅一方有战术组合时，有战术组合的一方数量逐渐增多，最终获胜。

由上述结果，可以看出本文所做的研究具有新意，为解释实际作战过程提供了新的理论基础。

[1] LANCHESTER F W.Aircraft in Warfare:The Dawn of the Fourth Arm[J].The Quaternary Research (Daiyonki-Kenkyu),2010,26:177-179.

[2] TAYLOR J G,BROWN G G.Annihilation prediction for Lanchester-type models of modern warfare[J].Operations Research,1983,31(4):752-771.

[3] MACKAY N.Lanchester combat models[J].Mathematics,2006(5):170-173.

[4] JOHNSON D D P,MACKAY N J.Fight the power:Lanchester's laws of combat in human evolution[J].Evolution and Human Behavior,2015,36(2):152-163.

[5] LAUREN M K.Characterising the Difference between Complex Adaptive and Conventional Combat Models[J].Physics,2012.

[6] LAUREN M K,SMITH J M,MOFFAT J,et al.Using the Fractal Attrition Equation to Construct a Metamodel of the Mana Cellular Automaton Combat Model[J].Physics,2006.

[7] LAUREN M K.A Metamodel for Describing the Outcomes of the Mana Cellular Automaton Combat Model Based on Lauren's Attrition Equation[J].Physics,2006.

[8] LAUREN M K,MCINTOSH G C,PERRY N,et al.Art of war hidden in Kolmogorov’s equations[J].Chaos:An Interdisciplinary Journal of Nonlinear Science,2007,17(1):013121.

[9] MOFFAT J,PASSMAN M.Metamodels and emergent behaviour in models of conflict[J].Simulation Modelling Practice and Theory,2004,12(7):579-590.

[10] PERRY N.Verification and Validation of the Fractal Attrition Equation[J].Verification & Validation of the Fractal Attrition Equation,2006.

[11] PERRY N.Fractal Effects in Lanchester Models of Combat[J].Fractal Effects in Lanchester Models of Combat,2009.

[12] LAUREN M,STEPHEN R.Map-aware non-uniform automata (MANA)-A New Zealand approach to scenario modelling[J].Journal of Battlefield Technology,2002,5(1):27-31.

[13] HELMBOLD R L.Historical Data and Lanchester's Theory of Combat Part II[J].Historical Data & Lanchesters Theory of Combat Part,1961.

[14] ILACHINSKI A.Land Warfare and Complexity,Part II:An Assessment of the Applicability of Nonlinear Dynamics and Complex Systems Theory to the Study of Land Warfare[J].1996.

[15] ILACHINSKI A.Irreducible Semi-Autonomous Adaptive Combat (ISAAC):An Artificial-Life Approach to Land Combat[J].Military Operations Research,2000,5(3):386.

[16] ILACHINSKI A.Exploring self-organized emergence in an agent-based synthetic warfare lab[J].Kybernetes,2003,32(1/2):38-76.

[17] 伍明,李琳琳,魏振华,等.移动机器人动态环境下目标跟踪异构传感器一致性观测方法[J].光学学报,2015,36 (6):194-202.

[18] 王林,彭辉,朱华勇,等.复杂环境下多无人机协作式地面移动目标跟踪[J].控制理论与应用,2011,28(3):300-308.

[19] 娄柯,齐斌,穆文英,等.基于反馈控制策略的多智能体蜂拥控制[J].浙江大学学报:工学版,2013,47(10):1758-1763.

[20] 陈世明,李慧敏,谢竟,等.基于局部估计的功率驱动多智能体网络牵制蜂拥控制算法[J].控制与决策,2013,28(8):1190-1194.

[21] YAMAUCHI S,KAWAMURA H,SUZUKI K.Application of Flocking Algorithm to Attitude Control of Humanoid Robot[C]//Intelligent Autonomous Systems 12.[S.l.]:[s.n.],2013:835-842.

[22] 谭东风.基于网络整体效能的战斗毁伤模型[J].系统工程理论与实践,2013,33(2):521-528.

[23] PROTOPOPESCU V.Combat modeling with partial differential equations[J].European Journal of Operational Research,1989,38(2):178-183.

[24] PROTOPOPESCU V,SANTORO R T,DOCKERY J.Combat modeling with partial differential equations[J].European Journal of Operational Research,1989,38(2):178-183.

[25] COSNER C,LENHART S,PROTOPOPESCU V.Parabolic systems with nonlinear competitive interactions[J].IMA Journal of Applied Mathematics,1990,44(3):285-298.

[26] FIELDS M A.Modeling Large Scale Troop Movement Using Reaction Diffusion Equations[J].Modeling Large Scale Troop Movement Using Reaction Diffusion Equations,1993.

[27] RUSU P.Two-dimensional combat modeling with partial differential equations[R].Oak Ridge National Lab.,TN (USA),1988.

[28] JAISWAL N K,NAGABHUSHANA B S.Combat modeling with spatial effects,reserve deployment and termination decision rules[J].Computers & operations research,1994,21(6):615-628.

[29] SPRADLIN C,SPRADLIN G.Lanchester’s equations in three dimensions[J].Computers & Mathematics with Applications,2007,53(7):999-1011.

[30] KEANE T.Combat modelling with partial differential equations[J].Applied Mathematical Modelling,2011,35(6):2723-2735.

[33] DURRETT R,LEVIN S.Spatial aspects of interspecific competition [J].Theor.Pop.Biol.1998,53:30-43.

[34] REICHENBACH T,MOBILIA M,FREY E.Mobility promotes and jeopardizes biodiversity in rock-paper-scissors games [J].Nature,2007,448:1046-1049.

[35] GILLESPIE D T.A general method for numerically simulating the stochastic time evolution of coupled chemical reactions [J].J.Comput.Phys.,1976,22:403-434.