纯电动Tip-In/Out工况的前馈校正与主动阻尼防抖控制∗
2018-03-01赵治国李蒙娜
赵治国,王 晨,,张 彤,李蒙娜
(1.同济大学新能源汽车工程中心,上海 201804; 2.科力远混合动力技术有限公司,上海 201501)
前言
复合功率分流混合动力系统电机直接与行星排连接,传动系中阻尼元件不足。系统纯电动运行时,电机转矩响应灵敏,在驱动转矩及扰动的快速、大幅激励下极易发生传动系扭转振动[1-2]。同时,电机低速转矩纹波也会加剧抖振幅度[3],严重影响整车驾乘舒适性。
文献[4]中针对单级减速传动系统进行分析,定位传动轴半径和长度以及减速器齿轮间隙为系统扭转振动的主要影响因素。文献[5]和文献[6]中分别应用前馈校正和加速度反馈来抑制转速闭环控制时的传动系扭转振动。文献[7]中针对共振频率超过100Hz的高速传动系统,采用改进PID控制器来抑制转速闭环控制时的传动系扭转振动。然而,上述策略均针对转速伺服控制,较难直接应用于基于转矩控制的混合动力汽车驱动系统。文献[3]中采用时频分析法定位定子绕组电流阶次分量引起的电机转矩波动是导致车辆纯电动起步纵向抖动的主要原因,通过在定子电压矢量坐标系中加入频率补偿器,以及对相电流传感器信号进行滤波处理,抑制电机相电流畸变。文献[8]中采用车速与电流双闭环控制策略,对纯电动汽车起步平顺性进行优化。然而,上述方案均落实在电机本体控制层面,限制了其应用范围。文献[9]中通过细分纯电动起步工况,采用多参数标定的方法对起步平顺性进行了优化。文献[10]中设计高阶滤波器将电机传感器误差等噪声信号剥离,再利用PD调节器进行反馈控制,抑制传动系的转速波动。文献[11]中通过实时计算部件转速跟踪误差,设计滑模变结构控制器对传动系扭转振动实施主动阻尼控制。文献[12]中基于轮速和电机反馈转矩,利用卡尔曼滤波器对输出端实际转矩进行观测,并与期望转矩进行偏差控制以改善传动系扭转振动。然而,上述策略的控制效果依赖准确的轮速信息,但车辆制动系统反馈的轮速信号存在通信延迟,并且在极低车速下不反馈轮速信号,其实际应用受到限制。
本文中分别设计前馈校正和主动阻尼防抖策略,以抑制功率分流式混合动力汽车纯电动工况下的传动系扭转振动。首先,考虑扭转减振器、传动轴和轮胎弹性,对复合功率分流式混合动力系统进行动态建模。然后,对动态模型进行简化,基于频域分析方法对系统扭转振动特性进行分析。其次,基于简化的双质量模型设计前馈校正器和轮速观测器,并对其极点配置方法进行研究。最后,以纯电动Tip-In/Out工况(将快速增加油门称为Tip-In工况,将快速释放油门称为Tip-Out工况)为例,对两种防抖策略进行仿真和实车验证。
1 系统建模
1.1 结构方案
如文献[13]和文献[14]中所述,复合功率分流式混合动力系统采用共用行星架和齿圈的双行星排结构。发动机经扭转减振器与变速器输入轴相连,电机1和电机2分别与小、大太阳轮相连,三者动力由行星排复合后经齿圈、传动系传递至轮边。湿式制动器1,2分别用于锁止行星架和小太阳轮。混合动力系统结构如图1所示,双行星排及混合动力变速器实物如图2所示,整车及动力系统参数见表1。

图1 复合功率分流式混合动力系统结构示意图

图2 双行星排及混合动力变速器实物
1.2 数学模型
忽略行星轮、太阳轮转动惯量及齿轮啮合间隙,图1所示复合功率分流式混合动力系统各轴动力学关系式为

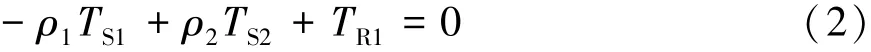
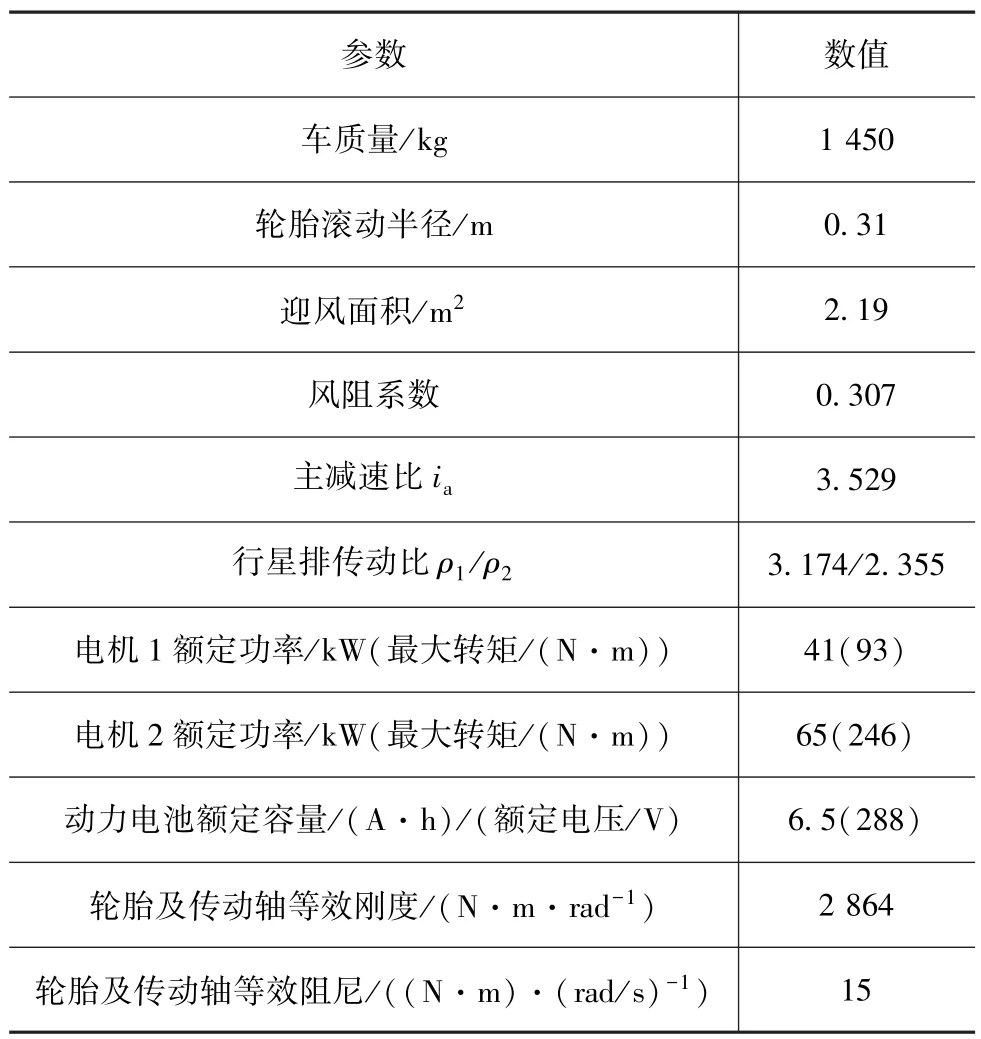
表1 整车和动力系统参数

式中:I,θ和T分别代表转动惯量、角位移和转矩;k和c分别代表等效刚度和等效阻尼;下标 ENG,MG1,MG2,TDS,TI,L 和 WH 分别代表发动机、电机1、电机2、扭转减振器、等效传动系、整车和车轮;下标S1,S2,C1和R1分别代表小太阳轮、大太阳轮、共用行星架和共用齿圈;m为整车质量;f为滚动摩擦因数;Cd为风阻系数;A为迎风面积;v为车速;i为坡度;δ为旋转部件的等效质量换算系数;r为轮胎半径;ia为主减速比。
1.3 纯电动模式
该复合功率分流式混合系统包含制动器1锁止和打开两种纯电动模式。为充分发挥系统纯电动模式下的动力性和经济性,优先采用制动器1锁止的纯电动模式[15]。此时,电机1和电机2可分别以速比ρ1,ρ2驱动车辆前行。两种驱动方式仅存在传动比和传动效率上的差别。下文仅以电机2单独驱动为例进行论述,该模式等效杠杆[16]如图3所示。

图3 电机2纯电动模式杠杆图
2 防抖策略设计
2.1 模型简化与分析
如图3所示,制动器1锁止时提供锁止转矩,发动机和扭转减振器对传动系的作用忽略不计。该模式下,系统简化为一仅包含单级主减速器的双质量模型,如图4所示。其动力学关系为

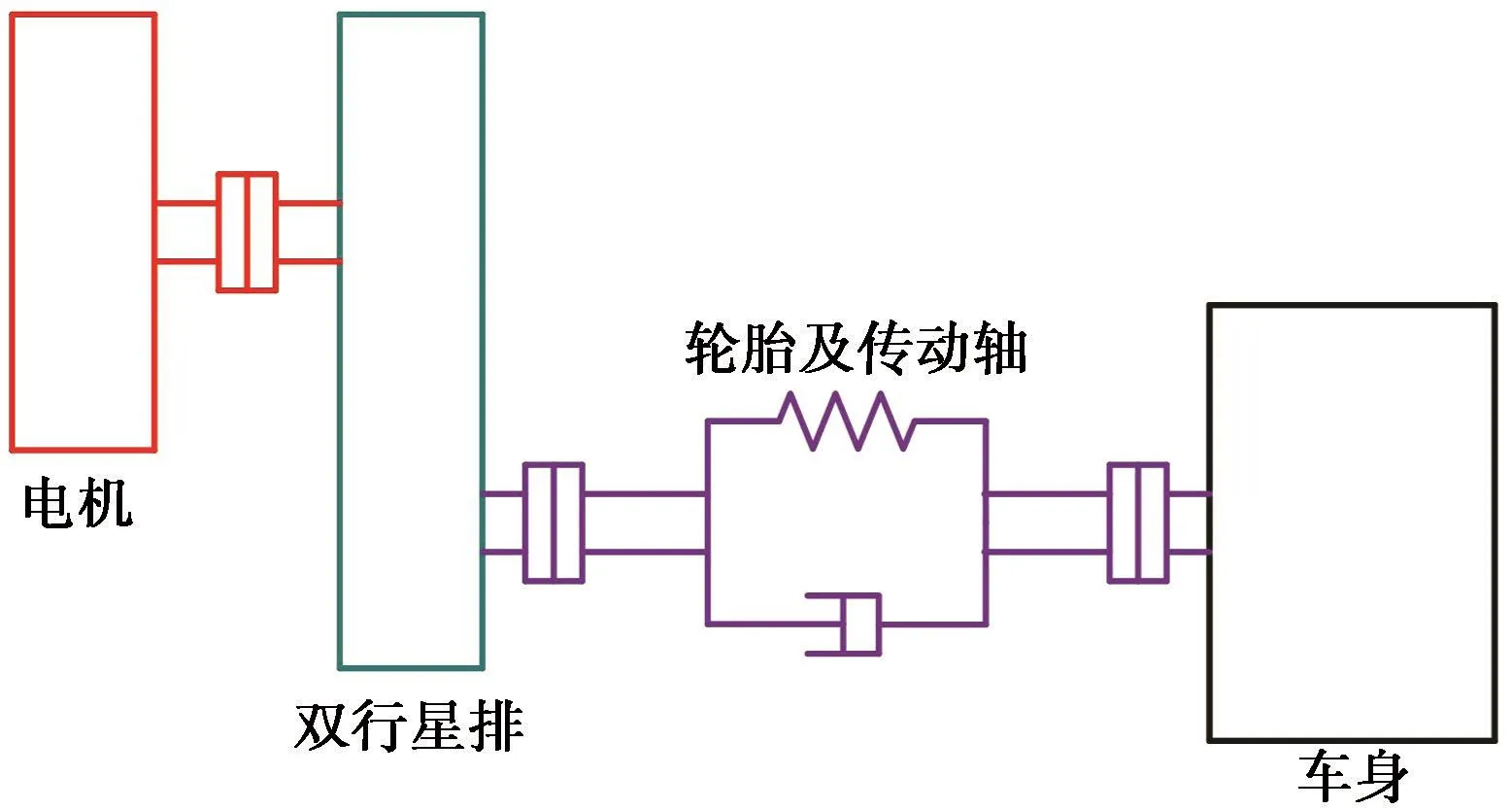
图4 系统简化模型

式中I′R1为齿圈输出端的等效转动惯量。
选取状态变量、控制变量和扰动分别为
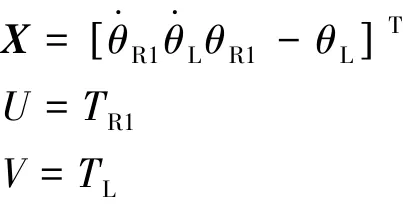
得简化后系统的状态方程为
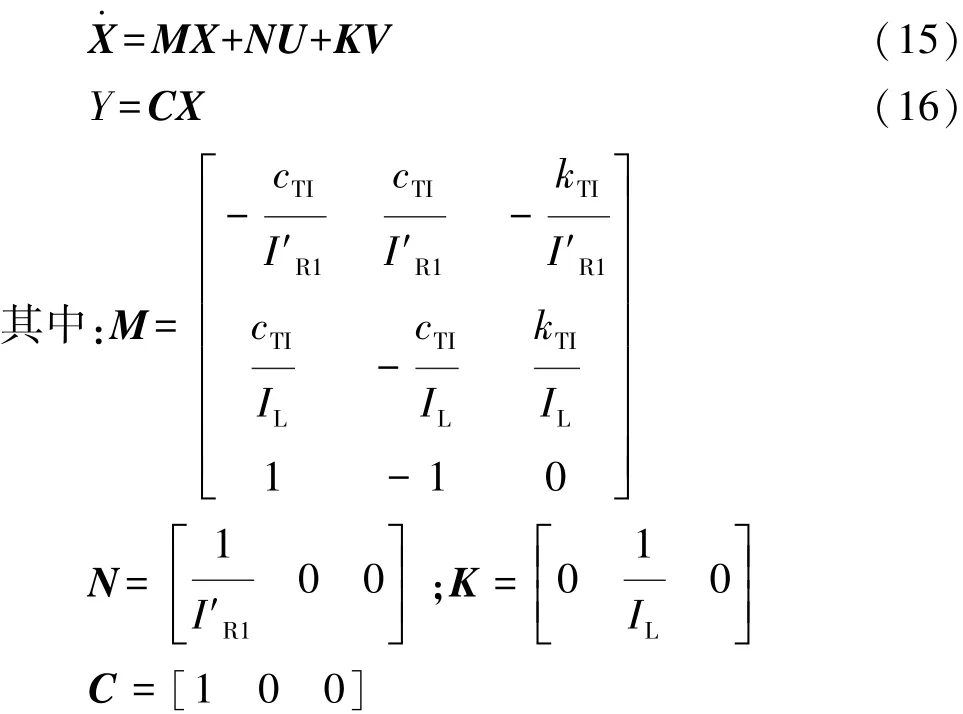
由式(15)得系统传递函数矩阵,其中齿圈转矩转速和齿圈转矩 轮速的传递函数表达式分别为
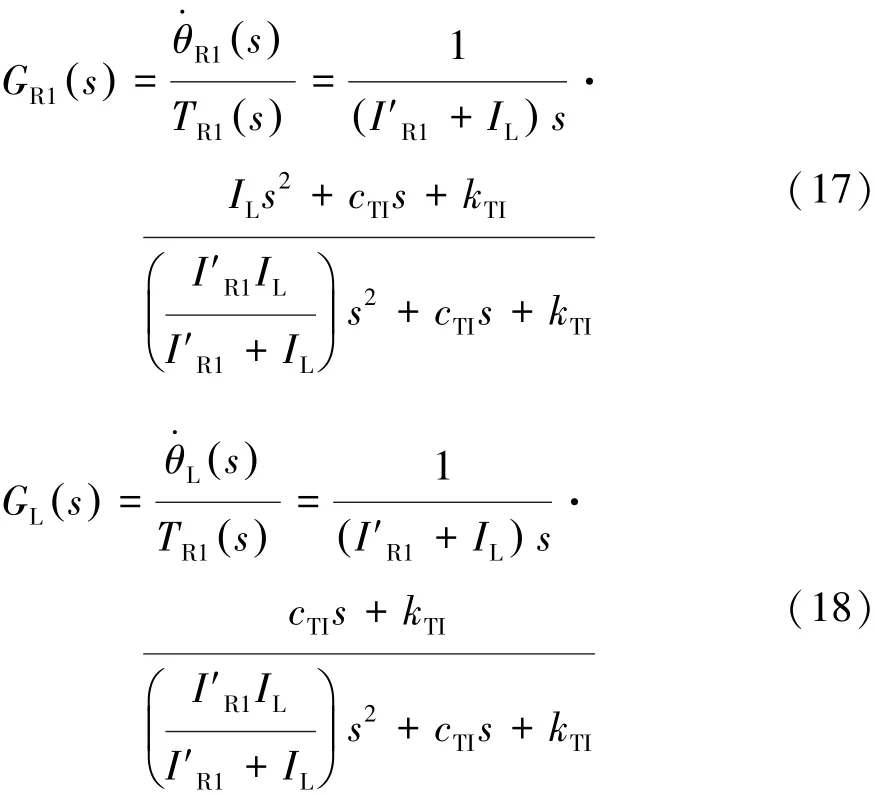
其中,式(17)的零极点分布如图5所示,式(17)和式(18)的对数幅、相频特性如图6所示。
由图5和图6可知:在齿圈转矩作用下,齿圈转速和轮速在2.74Hz频率范围附近产生低频共振,其中齿圈转速和轮速的对数幅频响应分别为-2.774和-26.01dB。该固有特性由接近虚轴但又不十分接近零点的一对共轭复极点-0.782+17.3i和-0.782-17.3i确定,其仅与齿圈等效转动惯量、整车等效转动惯量、传动轴和轮胎的等效刚度和等效阻尼有关。

图5 齿圈转矩 转速零极点分布
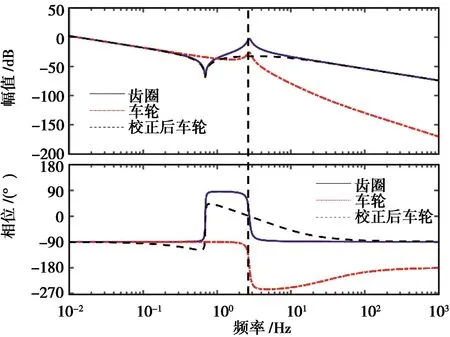
图6 齿圈转速、轮速幅频和相频特性
2.2 前馈校正防抖策略
2.2.1 控制策略设计
前馈校正防抖控制策略逻辑架构如图7所示。
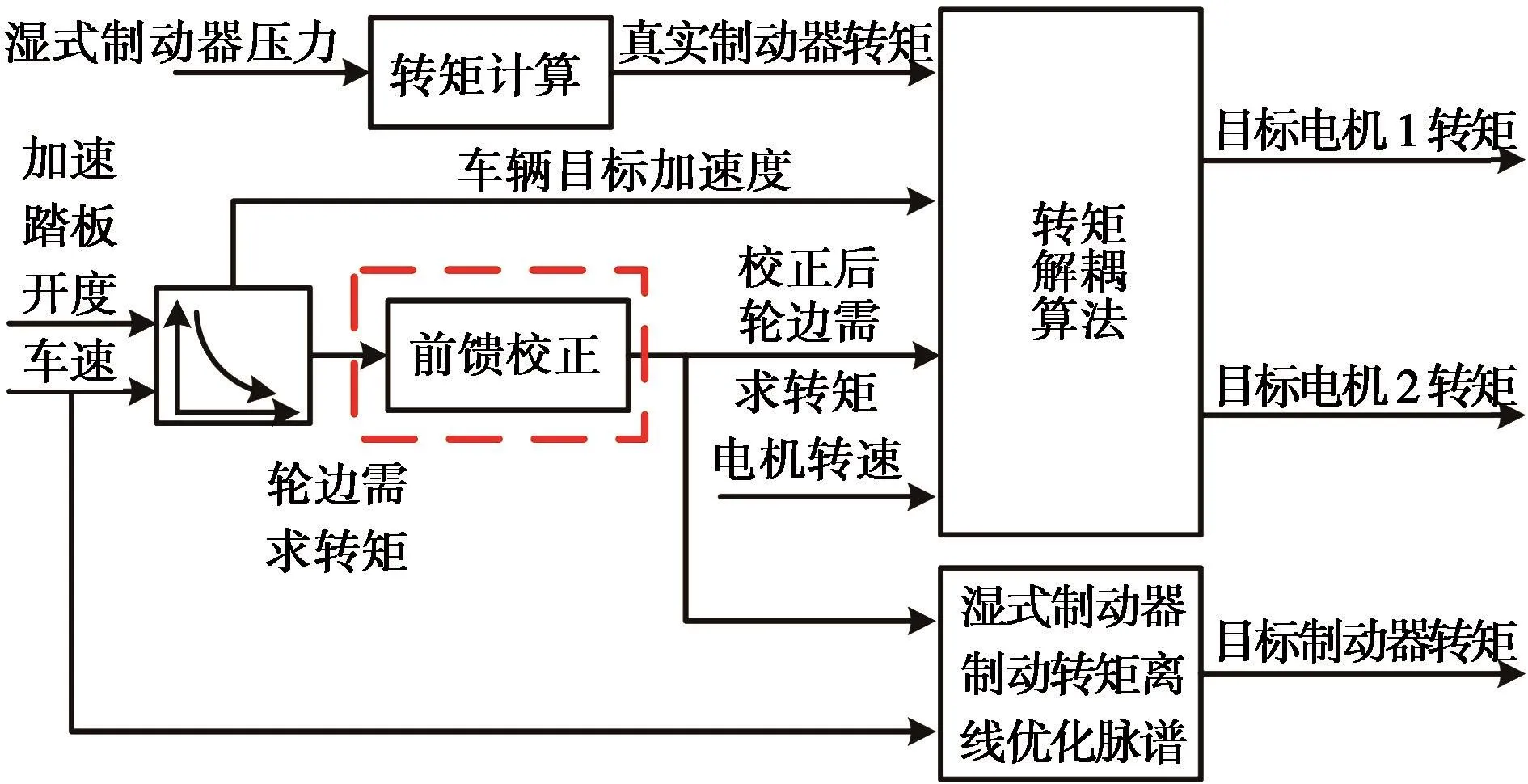
图7 前馈防抖控制策略逻辑架构
由图7可知:整车控制器根据加速踏板开度和车速查表获取轮边需求转矩和目标车辆加速度。其中前馈校正器对轮边需求转矩进行校正,校正后的轮边需求转矩和车速用于查表获取湿式制动器最优需求转矩,其中湿式制动器最优转矩脉谱[15]根据系统效率最优原则,采用瞬时优化方法在线计算得到。最后,整车控制器根据电机反馈转速、由制动器反馈压力计算而得的真实制动器转矩、校正后轮边需求转矩和目标车辆加速度,采用转矩解耦方法[17]实时计算电机目标需求转矩。
2.2.2 校正器设计
前馈校正器一方面通过引入新零点消除原主导极点对系统动态性能的不利影响,另一方面保证新增极点对系统动态特性无不利影响。
设计前馈校正器传递函数为
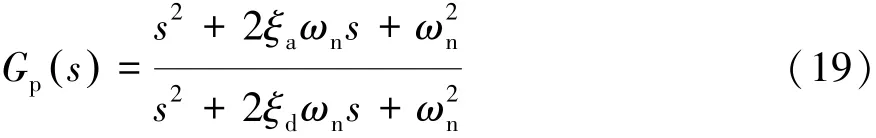
式中:ξa和ωn分别为原系统特征方程阻尼比和自然频率;ξd为校正器特征方程阻尼比。
该前馈校正器的幅频和相频特性如图8所示,其中幅频特性满足如下关系式:


图8 校正器幅频及相频特性
由图8可知:前馈校正器对指定频率附近的输入信号进行陷波,陷波幅值由设计人员根据系统性能指标给定,进而根据式(20)确定校正器特征方程阻尼比。校正器对指定频率附近信号的相频特性产生影响,对低于陷波频率一定范围的输入信号相位响应滞后,对高于陷波频率一定范围的输入信号相位响应超前,在指定频率附近的输入信号相位响应发生急剧变化。
本文中针对原系统的固有振动特性,将前馈校正器陷波幅值定为30dB,添加前馈校正器后的系统零极点分布和对数幅频、相频特性分别如图5和图6所示。
由图5可知,校正器相当于在原系统主导极点处引入一对新共轭复数零点,消除由原主导极点表征的系统低频共振特性的影响。同时,引入一对远离虚轴和原主导极点的实数极点,减轻前馈校正器自身对系统动态特性的影响。
由图6可知,校正后系统仅改变共振频率附近输入信号的幅频响应,对低于共振频率一定范围的输入信号的相位响应略有滞后,对高于共振频率一定范围的输入信号相位响应略有超前,远离共振频率处信号的幅频、相频特性与校正前保持一致。
2.3 主动阻尼防抖策略
2.3.1 控制策略设计
由图6可知,共振频率处,轮速的幅频响应约为齿圈转速幅频响应的1/10,即齿圈转矩对轮速动态特性的影响十分有限。考虑到纯电动模式下,轮速与齿圈转速具有固定速比关系,所以,将轮速经速比变换后作为齿圈转速的参考轨迹进行偏差控制,以实现传动系主动阻尼调节。其策略架构如图9所示。

图9 主动阻尼控制策略逻辑架构
由图7和图9可知,主动阻尼与前馈校正防抖策略的区别在于:根据齿圈实际转速和参考转速的偏差产生轮边补偿转矩,其中齿圈参考转速由观测轮速经速比变换而来。
2.3.2 观测器设计
齿圈实际转速可以根据电机反馈转速直接获取,而轮速和角度差则通过设计的观测器获取。将式(15)中整车负载转矩视为一种扰动,其与整车质量、坡度等因素有关,相对于齿圈转矩而言,该扰动不能突变。所以,将负载转矩作为状态变量并重写状态方程如下:
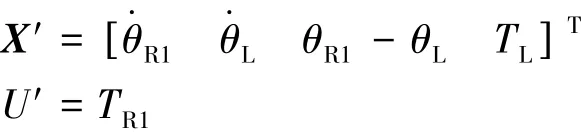
简化后系统的状态方程为

由式(21)和式(22)系数矩阵可知,系统可观测。所以,设计状态观测器:
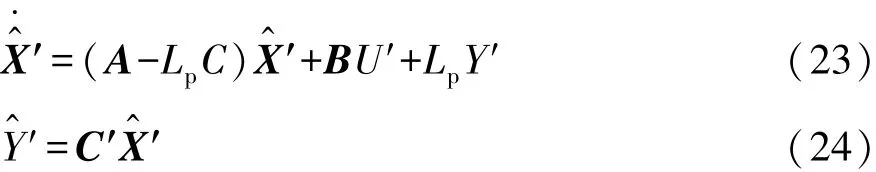
式中:Lp为观测器反馈增益;C′为观测器输出矩阵,C′=I;′为观测器状态变量;′为观测器输出变量。
2.3.3 极点配置
鉴于高阶系统的动态响应不仅与极点位置有关,还与零点位置有关。本文中分别以观测齿圈转速和轮速为例,描述观测器的极点配置方法。
假设轮速可测并对齿圈转速进行观测,则将式(22)原系统输出方程中的输出矩阵C替换为[0 1 0 0]。如图10所示,引入闭环反馈后,观测器极点由3个增加为4个,零点由2个增加为3个。为简化系统设计并加快观测器收敛速度,首先,根据典型2阶系统瞬态性能指标确定观测器的阻尼系数和自然频率,由此确定观测器的两个极点位置。然后,将观测器的另两个极点位置配置在实轴上,并且距虚轴的距离5倍于前两个极点距虚轴的距离,使前两个极点成为主导极点。
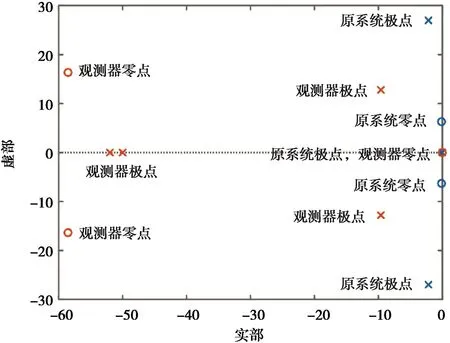
图10 齿圈转速观测器极点配置
由图10可知,两个复数共轭零点距虚轴的距离远大于两个主导极点距虚轴的距离,其对系统动态特性的影响可以忽略。系统简化为仅包含一个闭环零点和两个闭环共轭极点的2阶系统,其标准形式下的阶跃响应为
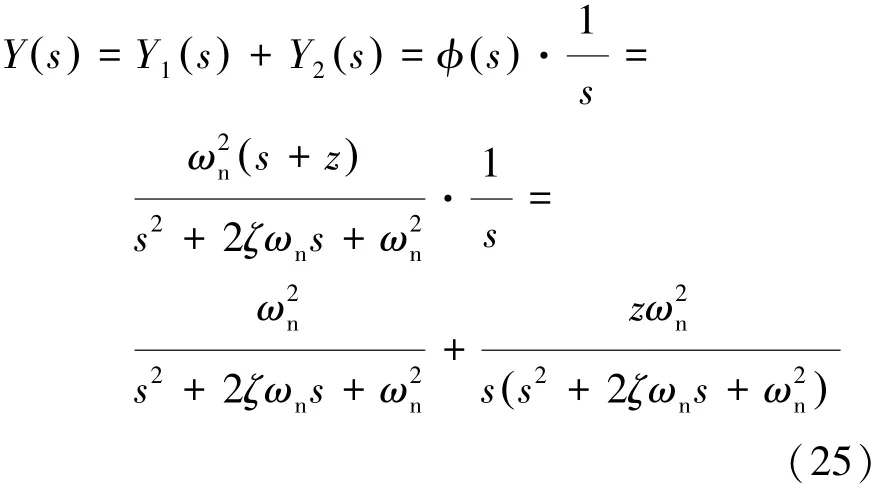
由于0<ζ<1,式(25)取拉氏反变化后得系统在时域坐标下的阶跃响应为

由于观测器闭环零点处于原点(即z=0),则时域响应中由零点引起的分量y2(t)为零,系统的动态特性完全由闭环极点决定。当观测器采用不同的阻尼比和角频率时,齿圈转速的观测结果如图11所示。

图11 齿圈转速观测结果
由图11可知:观测器的收敛速度与目标极点的位置有关(即与简化后的2阶闭环系统的阻尼比和角频率有关)。阻尼比越大,超调量越小;角频率越大,调整时间越短。所以,首先根据超调量指标确定观测器阻尼比。然后,固定阻尼比并增加角频率,使观测器维持较小超调量的同时缩短调整时间。
假设齿圈转速可测并对轮速进行观测,则维持系统输出矩阵C不变。如图12所示,引入闭环反馈后,观测器极点由2个增加为4个,零点由1个增加为3个。由式(26)可知,位于原点处的闭环零点对系统动态响应无影响,而另外一对共轭复数零点接近虚轴并远离原点,其使根轨迹向左移动或弯曲,有助于提升系统稳定性,缩短瞬态过程时间。现将两组极点距虚轴的距离配置相差5倍以上,则系统简化为一包含2极点、2零点的2阶系统,系统动态性能取决于零点和极点的距离。配置不同极点位置的轮速观测结果如图13所示。
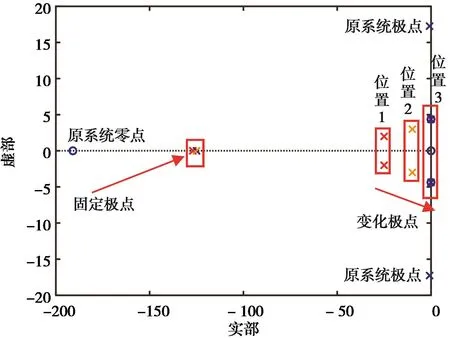
图12 轮速观测器极点配置

图13 轮速观测结果
由图12和图13可知,两个闭环复数共轭极点越接近两个闭环复数共轭零点,系统的动态响应越好。当其完全重合(形成一对偶极子)时,系统的动态响应最佳。
3 仿真与结果分析
采用Matlab/Simulink软件对图1所示混合动力系统、图7和图9所示防抖策略进行建模。其中将校正器方程式(19)、观测器方程式(23)和式(24)经Z变换从连续时间域转换至离散时间域,并将仿真步长设置为0.002s。以低车速全油门Tip-In/Out工况为例进行对比仿真,整车及关键零部件参数如表1所示,控制前后的齿圈需求转矩、齿圈实际转速以及整车冲击度[18]分别如图14~图16所示。
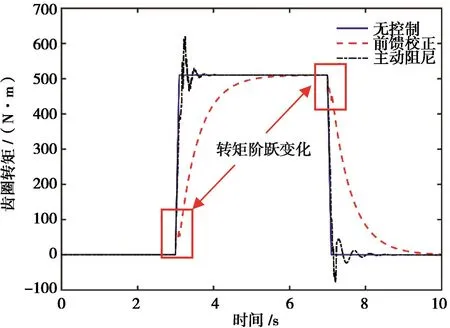
图14 控制前后齿圈需求转矩

图15 控制前后齿圈转速
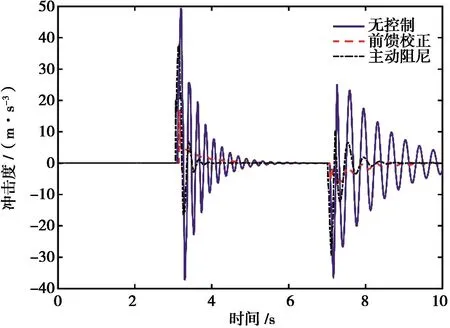
图16 控制前后整车冲击度
由图14可知,防抖控制前,齿圈需求转矩呈方波变化,阶跃时间约为0.1s。主动阻尼控制后,齿圈需求转矩围绕原始目标转矩叠加阻尼转矩,转矩上升阶段超调量为21.6%、调整时间为0.41s(取误差带宽度5%),转矩下降阶段超调量为15.3%、调整时间为0.36s。前馈校正后,齿圈需求转矩上升时间为1.93s,转矩变化先急后缓,变化梯度总体1阶连续,仅在Tip-In阶段3~3.11s处和 Tip-Out阶段7~7.11s处,转矩有阶跃变化。
由图15可知:防抖控制前,在Tip-In/Out初期齿圈转速有明显波动并逐渐衰减,Tip-In/Out阶段转速波动峰峰值最大分别达450.2和355r·min-1;主动阻尼控制后,Tip-In/Out阶段齿圈转速波动最大峰峰值分别为256.9和232r·min-1,分别比控制前下降43%和34.7%。尽管主动阻尼控制对齿圈初始转速波动抑制效果有限,但转速调节时间相比不施加控制时明显缩短。前馈校正后,Tip-In/Out阶段齿圈转速均无明显波动,上升速率与校正前无明显差异,但转速上升时间相对校正前延迟0.47s。
由图16可知,防抖控制前,在Tip-In/Out阶段整车冲击度波动剧烈,但逐渐衰减,整车冲击度分别在3.2和 7.17s达到峰值 49.33和-36.76m·s-3。主动阻尼控制后,Tip-In/Out阶段整车冲击度从第2个振荡周期开始快速衰减,其分别在3.15和7.11s达到峰值37.74和-29.48m·s-3,分别降低 23.5%和19.8%。前馈校正后,在Tip-In/Out阶段整车冲击度振荡明显减弱,分别在3.17和7.34s达到峰值17.08和-5.93m·s-3,与无控制相比分别降低65.4%和83.9%。
由上述可知:前馈校正和主动阻尼控制通过校正或补偿齿圈转矩,有效抑制Tip-In/Out工况下整车冲击度和齿圈转速波动,改善整车驾驶平顺性。其中,前馈校正策略的振动抑制效果好,但牺牲了整车动力性;而主动阻尼策略的初期抖动抑制效果不佳,但整车动力性表现较好。
4 实车试验与结果分析
将图7前馈校正策略移植至整车控制器并维持控制器执行周期为0.01s。为提升轮速观测精度和阻尼控制效果,将图9轮速观测器和主动阻尼控制策略移植至电机控制器并加快执行周期至0.002s。其余部分策略移植至整车控制器,并维持执行周期0.01s。整车控制器将驱动的电机目标转矩发送给电机控制器,由电机控制器在驱动转矩基础上叠加主动阻尼转矩。
试验中,齿圈需求转矩和齿圈转速波动通过采集整车控制器内部信号获取,整车冲击度则通过对安装在座椅导轨上纵向加速度信号进行微分、低通滤波后获取。试验环境如图17所示,试验结果分别如图18~图20所示。

图17 实车试验环境
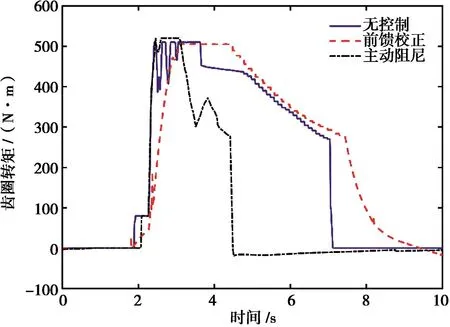
图18 控制前后齿圈需求转矩
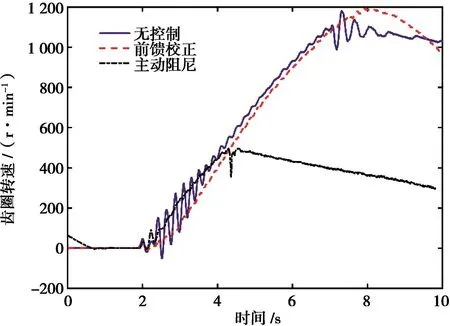
图19 控制前后齿圈转速

图20 控制前后整车冲击度
由图18可知:防抖控制前,2.26s进入Tip-In阶段,齿圈需求转矩上升时间为0.55s,到达峰值后因电机能力受限(转速波动引起)转矩出现振荡,3.07至3.61s转矩维持峰值输出,随后因动力电池功率受限逐渐下降,7.04s进入Tip-Out阶段,齿圈需求转矩下降时间0.08s且无转矩波动;主动阻尼控制后,齿圈需求转矩仅在Tip-In阶段初期叠加补偿转矩,随后平稳约0.7s后下降,经过一个较大波动后,在约4.5s时进入Tip-Out阶段,转矩急剧下降至零;前馈校正后,Tip-In阶段齿圈需求转矩上升时间为1.27s,在Tip-In阶段,转矩有两处阶跃变化至4.38s时,因动力电池功率受限开始逐渐下降,7.44s进入Tip-Out阶段,齿圈需求转矩先急后缓地下降,其间在8.18s处,转矩有小阶跃变化。
由图19可知:防抖控制前,在Tip-In/Out初期齿圈转速波动明显并逐渐衰减,Tip-In/Out阶段转速波动峰峰值最大分别达 246.26和 196.3r·min-1;主动阻尼控制后,Tip-In/Out初始阶段齿圈转速波动较小,峰峰值分别降至65和148r·min-1,且转速波动后被快速抑制,调整时间明显缩短;前馈校正后,Tip-In/Out阶段齿圈转速均无明显波动,上升速率与校正前无明显差异,但转速上升时间相对校正前延迟0.16s。
由图20可知:防抖控制前,在Tip-In/Out阶段初期,整车冲击度波动明显,Tip-In/Out阶段整车冲击度分别在 2.48和 7.36s达到峰值 57.98和-37.65m·s-3,随后逐渐衰减;主动阻尼控制后,在Tip-In/Out阶段初期整车冲击度波动明显减小,分别在2.40和4.59s达到峰值 15.73和26.81m·s-3,然后被快速抑制,抑制后的平均幅值维持在15m·s-3以内;前馈校正后,在 Tip-In/Out阶段整车冲击度均无明显波动,幅值维持在10m·s-3以内。
综上所述,前馈校正和主动阻尼防抖策略的试验结果与仿真结果基本一致。可见,通过校正或补偿齿圈需求转矩,能够有效抑制Tip-In/Out工况下整车冲击度和齿圈转速波动,改善整车驾驶平顺性。
5 结论
本文中基于传动系模型设计前馈校正器和轮速观测器,并对齿圈转矩进行校正和补偿控制,有效抑制复合功率分流式混合动力轿车纯电动Tip-In/Out工况的整车纵向抖振。主要结论如下:
(1)前馈校正器能够对指定频率范围内的齿圈转速响应进行陷波,陷波幅值可任意配置,但由于前馈控制属于开环控制,其控制效果依赖准确的系统结构参数;
(2)通过轮速观测器能够快速、精确地观测轮速,当轮速观测器的两个闭环极点与闭环零点构成一对偶极子时,观测器性能最佳;
(3)利用观测轮速并实施齿圈转速闭环控制,能有效抑制整车纵向冲击和齿圈转速波动,由于采用闭环控制,其对传动系中因扰动或参数变化引起的转速波动同样能产生抑制效果。
为提高前馈校正控制的自适应性,和主动阻尼控制的鲁棒性,下一阶段工作将着眼于传动系扭振频率的在线识别和观测器噪音的抑制。
[1] LA C,POGGI M,MURPHY P,et al.NVH considerations for zero emissions vehicle driveline design[C].SAE Paper 2011-04-1545.
[2] SYED F U,KUANG M L,YING H.Active damping wheel-torque control system to reduce driveline oscillations in a power-split hybrid electric vehicle[J].IEEE Transactions on Vehicular Technology,2009,58(9):4769-4785.
[3] 张立军,郑鹏,孟德建,等.混合动力轿车纯电动模式起步时纵向抖振的试验研究与控制[J].汽车工程,2013,35(3):212-218.
[4] VALENZUELA M A,BENTLEY J M,LORENZ R D.Evaluation of torsional oscillations in paper machine sections[J].Industry Applications, IEEE Transactions on,2005,41(2):493-501.
[5] VALENZUELA M A,BENTLEY J M,VILLABLANCA A,et al.Dynamic compensation of torsional oscillation in paper machine sections[J].Industry Applications, IEEE Transactions on,2005,41(6):1458-1466.
[6] MAKKAPATI V P,REICHHARTINGER M,HORN M.Performance improvement of servo drives with mechanical elasticity via extended acceleration feedback[C].Control Applications(CCA),2012 IEEE International Conference on,2012:1279-1284.
[7] MUSZYNSKI R,DESKUR J.Damping of torsional vibrations in high-dynamic industrial drives[J].IEEE Transactions on Industrial Electronics,2010,57(2):544-552.
[8] 汪贵平,马建,杨盼盼,等.电动汽车起步加速过程的动力学建模与仿真[J].长安大学学报(自然科学版),2009(6):98-102.
[9] 胡建军,杜瑞,吉毅.纯电动汽车起步控制策略[J].重庆大学学报,2013,36(8):19-25.
[10] BANG J S,KO Y-K,JUNG T-H.The active damping control to reduce driveline oscillations for electric vehicles using wheel speeds[C].SAE Paper 2015-01-1113.
[11] KOU Y S,WESLATI F.Development of a hybrid powertrain active damping control system via sliding mode control scheme[C].SAE Paper 2013-01-0486.
[12] AMANN N, BOCKER J, PRENNER F.Active damping of drive train oscillations for an electrically driven vehicle[J].IEEE/ASME Transactions on Mechatronics,2004,9(4):697-700.
[13] YU Haisheng, ZHANG Jianwu, ZHANG Tong.Control strategy design and experimental research on a four-shaft electronic continuously variable transmission hybrid electric vehicle[J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2012,226(12):1594-1612.
[14] 赵治国,代显军,王晨,等.复合功率分流混合电动轿车驱动模式切换的协调控制[J].汽车工程,2015,37(3):260-265.
[15] ZHAO Z,WANG C,ZHANG T,et al.Control optimization of a compound power-split hybrid transmission for electric drive[C].SAE Paper 2015-01-1214.
[16] BENFORD H L,LEISING M B.The lever analogy:A new tool in transmission analysis[C].SAE Paper 810102.
[17] 赵治国,王晨,张彤,等.复合功率分流变速器的设计与验证[J].汽车工程,2015,37(4):407-415,390.
[18] 张俊智,李波,薛俊亮,等.混合动力电动汽车冲击度的试验[J].机械工程学报,2008,44(4):87-91.
