考虑过街行人运动不确定性的人-车碰撞伤害评估∗
2018-03-01刘象祎宋晓琳
黄 智,何 颖,刘象祎,宋晓琳
(湖南大学,汽车车身先进设计与制造国家重点实验室,长沙 410082)
前言
行人是交通事故中易受伤害的群体,2013年世界卫生组织(WHO)的报告指出,在因交通事故死亡的人数中,行人约占22%[1]。围绕行人保护问题,国内外研究人员开展了大量研究工作[2],重点集中在行人检测、避撞规划与动力学跟踪控制,并有成熟的产品装备应用,如Volvo的行人避撞系统。文献[3]中提出利用纵向制动实现行人避撞,避撞车速达35km/h。文献[4]中提出采用转向操作避免人-车碰撞,并研究了车辆避撞路径规划问题。文献[5]中则提出通过制动和转向两种操作以避免碰撞或降低碰撞伤害,从而达到行人保护的目的。上述研究的车辆避撞路径规划与避撞操作均以行人保持当前运动状态的假设为前提。然而行人在过街时的运动轨迹表现出一定随机性[6-7],受到如年龄、身高、性别、目的地、交通状况、情绪与经验等诸多因素的影响,导致在过街过程中可能随时改变行走的方向与速度。因此,采用恒速模型(constant velocity,CV)[8]预测的行人轨迹将存在误差,影响行人碰撞预警/避撞系统的准确性和可靠性,导致虚警或漏警,甚至可能因避撞操作而伤害行人。
由于影响行人运动轨迹的因素如情绪、经验和疾病状态等难以方便获得,有研究采用随机或概率模型描述行人运动。文献[9]中在观察行人轨迹基础上建立行人行走的几何概率模型。文献[10]中通过分析行人起始步态来判断行人意图,在此基础上,文献[11]中进一步提出分段线性模型和S模型来预测行人轨迹。文献[12]中提出对已有的轨迹数据进行学习并建立数据库,据此对行人运动进行分类并预测运动轨迹。文献[13]中建立了行人运动的随机模型,利用概率描述人-车碰撞风险。上述研究通过考虑行人运动的不确定性,获得碰撞概率预测,会显著提高人-车碰撞预测的可靠性。行人避撞系统的目的是避免或降低行人碰撞的伤害,然而如何评估行人运动不确定条件下,各种避撞操作仍可能造成的行人伤害,并选择合适的避撞策略,从已有的文献来看,尚未有深入的研究报道。
本文中研究的基本思路如下:考虑行人运动的不确定性,采用随机模型描述行人运动;利用无味变换实现行人轨迹的预测误差到人-车碰撞概率、碰撞速度分布的非线性映射;基于碰撞速度概率分布和人体碰撞生物力学的研究成果,评估行人所受到的伤害。
在描述人-车碰撞问题的基础上,设计无味变换预测人-车碰撞概率和碰撞速度分布的算法;结合现有行人碰撞伤害的研究成果,研究行人伤害概率的计算方法;最后通过仿真验证碰撞与伤害概率预测的准确性,并与确定性方法在各种避撞操作下的行人伤害预测结果进行对比。
1 人-车碰撞问题建模
1.1 车辆模型
以车辆沿道路行驶方向为x轴方向,垂直x方向指向车辆左侧为y轴方向,建立大地坐标系描述行人和车辆的运动。
假设驾驶员保持油门开度和转向盘转角,采用恒曲率和加速度模型(CCA)[14]描述车辆运动:
式中:xv(t),yv(t),vv(t),θv(t)分别为 t时刻车辆的x,y坐标、速度和航向角;av(t)为t时刻车辆的加速度;γv(t)为t时刻车辆的横摆角速度。
1.2 行人模型
采用1阶马尔科夫过程[15]描述行人运动,其中x方向的运行状态描述为
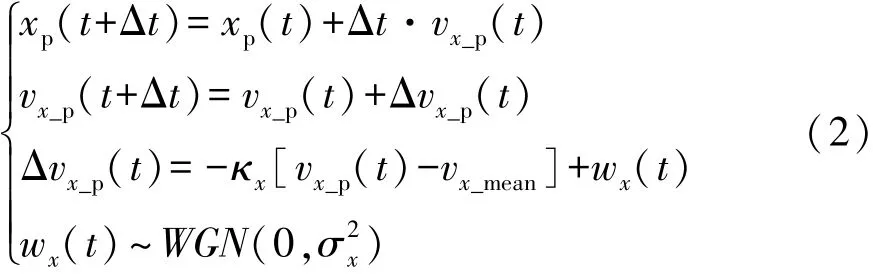
式中:xp(t),vx_p(t),Δvx_p(t)分别为 t时刻行人在 x轴方向的位置、速度和速度增量;wx(t)为行人沿x方向速度增量的随机扰动,用高斯白噪声描述;vx_mean为行人速度均值,服从 N(μx,σ2xm)分布;κ为1阶马尔科夫过程时间常数的倒数。
由模型描述可知,行人速度在其速度均值上下波动。行人在y方向的运动用相同模型描述。轨迹仿真步长Δt取0.5s,正常行人的步速率约为2Hz,并假定行人在起步时改变其速度和方向。
为得到行人横穿道路时沿x,y方向运动的特征,采集了无信号灯控制路口214个行人横穿道路的轨迹数据,经统计分析,得到运动参数为

1.3 碰撞时间(time to collision, TTC)[16-17]
当行人与车辆的轮廓重叠时,人-车发生碰撞。假设车辆定位中心(即车辆定位传感器的位置,本文中位于风窗玻璃上方中点)到前保险杠的最远距离约1.7m,并将行人简化成半径0.3m的圆柱体,人-车距离d定义为
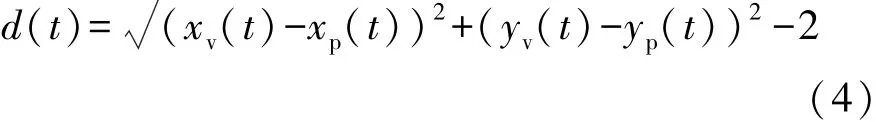
若 d(t)>0,∀t∈T,T为预测时长,在预测时长内没有发生人-车碰撞,TTC=∞,否则:
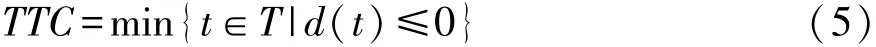
采用二分法计算预测时间T内的人 车最小距离dmin和d(t)≤0的最早时刻,直到时间误差小于0.01s为止。
1.4 碰撞速度
当碰撞发生时,碰撞速度vc由车辆初始速度vv(0)、碰撞时间TTC和车辆加速度av(t)计算得到;当碰撞不发生时,取人-车碰撞速度为0:

2 人-车碰撞风险估计
2.1 碰撞概率与TTC概率分布
采用碰撞概率和TTC的概率分布描述人-车碰撞事件。碰撞概率定义为式中pd(x)为最小距离概率密度函数。

TTC概率定义为
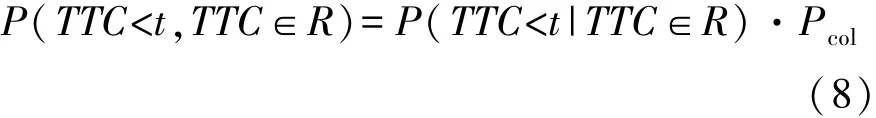
因直接计算P(TTC<t|TTC∈R)不方便,可用伪TTC(TTC)的概率近似描述[18],TTC定义为


式中td_min表示在预测时间T内达到最小距离dmin的时刻。则有
根据CCA模型假设,车辆加速度为恒值av,由TTC 概率密度pt(x)得到碰撞速度概率密度pv(x)为
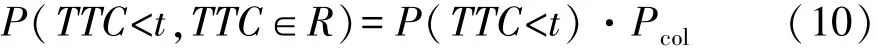
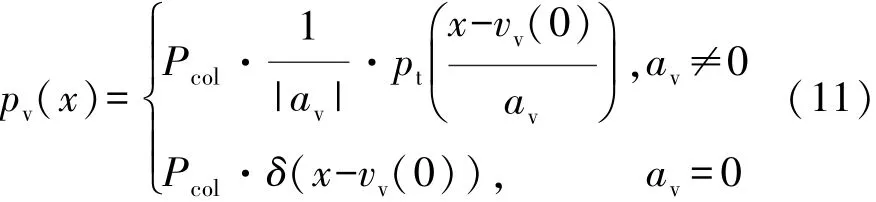
式中 δ(x-vv(0))表示在 x=vv(0)时函数值为+∞。
2.2 碰撞概率的模型描述
为确定P(TTC <t)和Pcol的数学模型,利用蒙特卡洛(MC)方法对某人-车冲突场景进行10 000次采样,得到预测碰撞频次、dmin和TTC 的直方图。
图1为某一交通场景下MC采样结果,采用高斯函数拟合dmin和TTC 的概率密度分布,得到dmin和TTC 的均值和均方根。
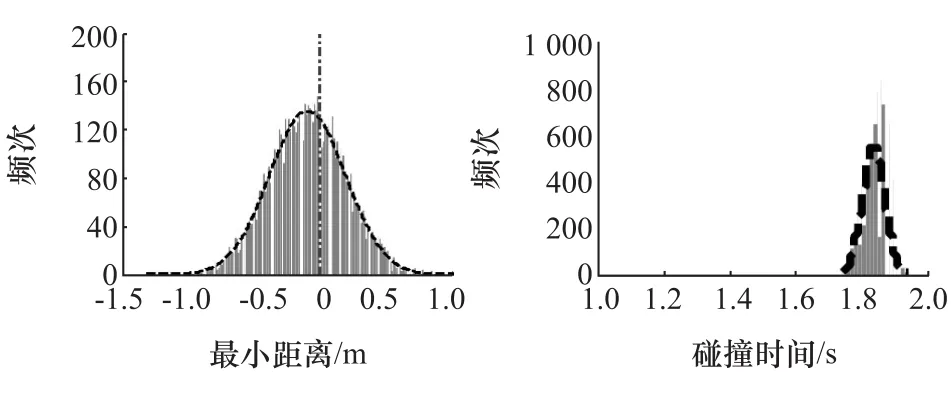
图1 MC采样dmin和TTC 频次直方图与高斯拟合
2.3 无味变换估计碰撞概率
研究采用无味变换(UT)[18-20]估计行人运动不确定性导致的人-车碰撞概率分布。取预测时长为2s,步长0.5s,假定车辆和行人的初始状态观测无噪声,行人模型的输入变量为
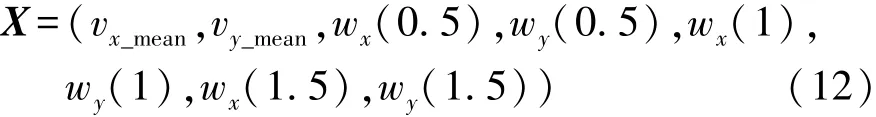
变量均值:

X的方差:



σ点集满足如下条件:
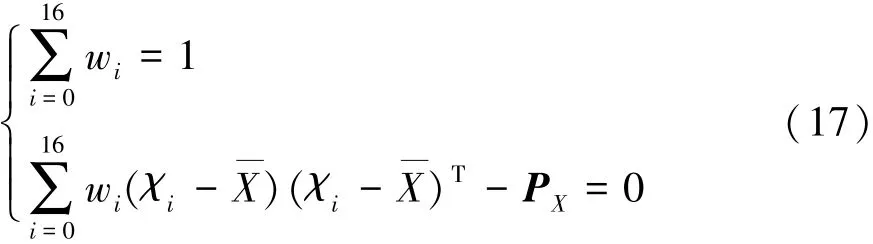
通过运动仿真得到对应的dmin和TTC的σ点集,进一步可得到dmin与TTC的均值与方差为
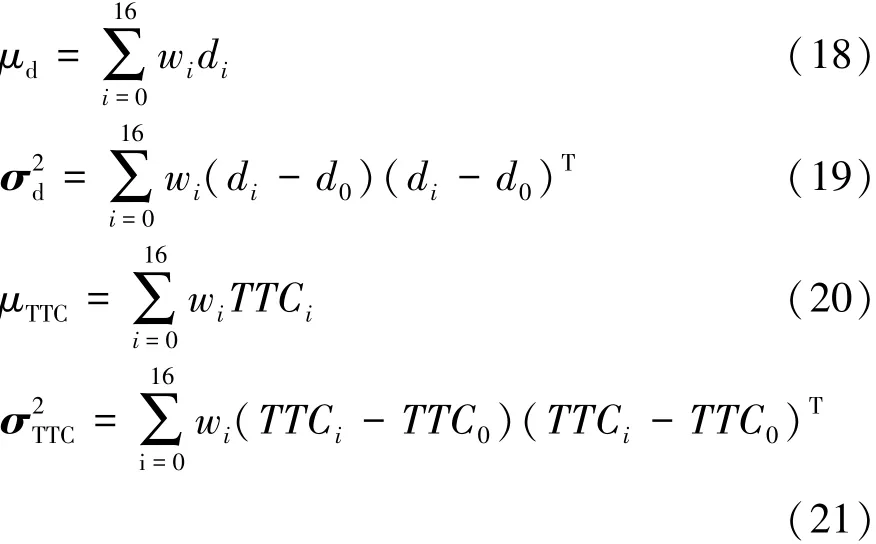
式中 di和 TTCi为对应的 σ点集元素。由 μd,σ2d,μTTC,计算碰撞概率和TTC概率密度。
3 伤害等级评估
文献[21]中采用AIS等级评分的方法评价人-车碰撞对行人造成的伤害,并在此基础上用轻伤、重伤、死亡3种伤情对AIS等级进一步归类。文献[22]中通过对国内交通事故数据的统计分析得到碰撞伤害与碰撞车速的关系,并以S函数给出了行人伤害严重程度概率与碰撞速度的关系为

式中:AIS3+表示包括AIS3及其以上的所有等级;AIS5+表示包括AIS5及其以上的所有等级。利用轻伤概率Pl、重伤概率Ps和死亡概率Pf对伤害程度概率进一步归类:
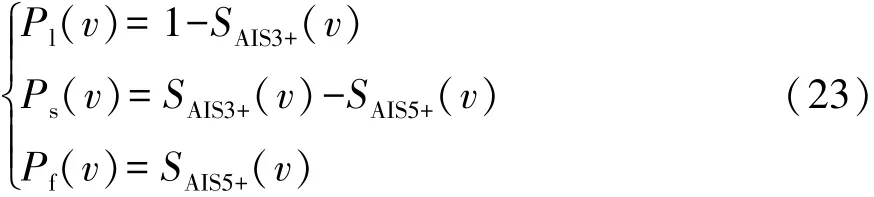
上述归类关系示意图如图2所示。
碰撞伤害程度的概率为

式中:i=l,s,f;vc_max,vc_min分别为碰撞速度的上下限。
4 仿真
4.1 人-车冲突场景
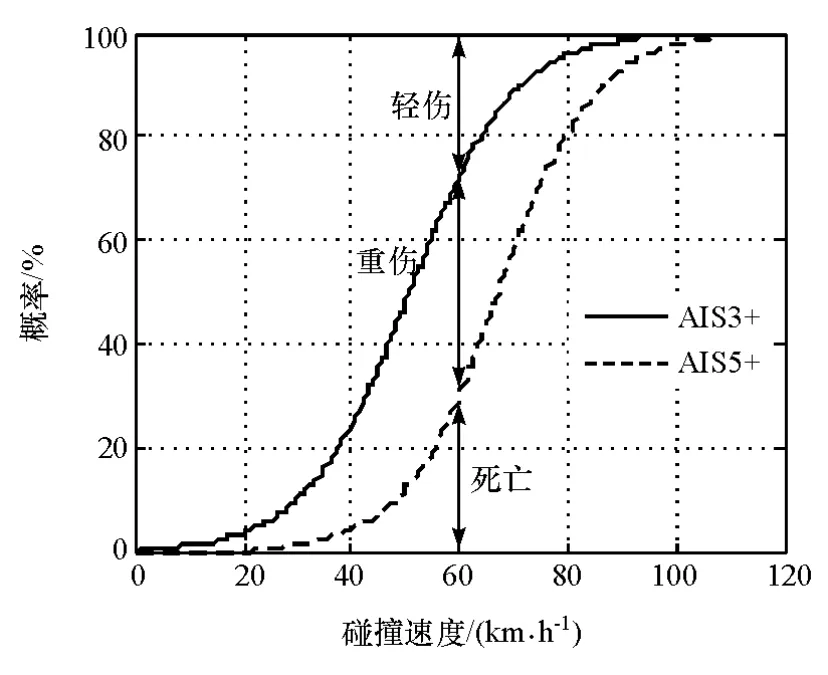
图2 伤害程度概率与碰撞速度的关系
因大量的人-车冲突的道路实验成本和风险过高而难以采取,另外受控条件下的样车实验也会由于行人和驾驶员的主观因素影响,与实际情况存在偏差。为验证所提出的方法,进行了仿真,以10 000次MC采样作为参考值,与UT计算的结果进行对比。
假定行人以一定初始速度横穿道路,车辆在距离行人一定的初始纵向(x向,用xv(0)-xp(0)表示)和横向(y向,用yv(0)-yp(0)表示)距离,沿正前方向行驶。为覆盖各种行人过街时人-车冲突场景,其参数设置如表1所示。

表1 人-车冲突场景的参数范围
4.2 伤害程度估计对比
在设定的参数变化范围内随机抽取5 000个场景,以覆盖各种人-车冲突场景。MC与UT方法得到的行人伤害概率如图3所示。
由图3可知,UT预测结果与MC方法采样结果较吻合(集中在对角线上),表明本文中提出的方法能较准确地预测行人伤害,偏差如表2所示。

表2 UT预测行人伤害与MC方法的偏差
4.3 各种避撞操作下的行人伤害
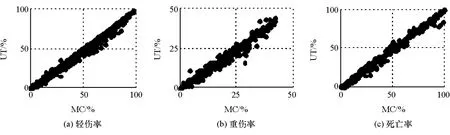
图3 MC与UT预测的行人伤害概率
冲突场景如表3所示。在该工况下预测采取不同的避撞操作(减速、转向、减速加转向等)时行人的伤害。避撞操作具体描述见表4,所述的左/右偏移操作如图4所示,偏移轨迹规划采用单点预瞄[23],预瞄距离为当前人-车纵向距离的0.9倍。将本文中的方法与比较常用的确定性方法预测的行人伤害进行对比,对比方法采用CV模型描述行人运动,车辆运动由采用的避撞操作描述。行人伤害的预测结果如图5所示,图中“CV”表示用确定性方法的预测结果,“UT”表示用本文提出的方法预测的结果。

表3 工况参数
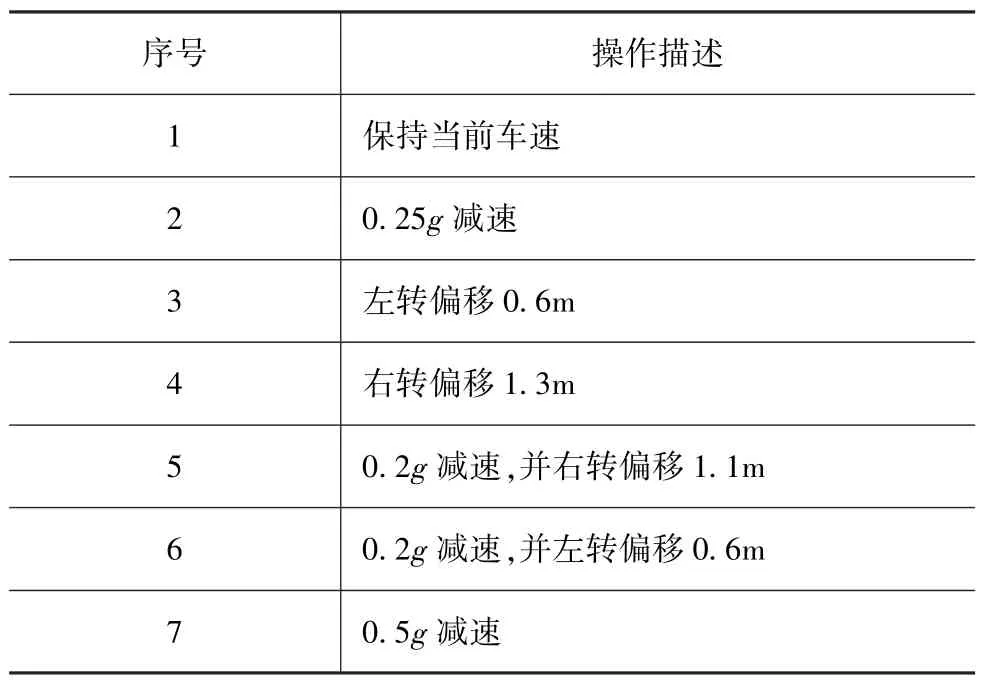
表4 不同避撞操作描述
当驾驶员不采取避让操作(保持恒速,即操作1)时,两种方法预测的碰撞概率均为100%,且由于车速不变,预测的伤害程度概率基本一致。对于确定性方法,预测的结果只有碰撞或不碰撞两种。当车辆减速度相同时,无论是否采取左右转向的避撞操作,若预测发生碰撞,其对应的行人伤害概率均相同,如采取避撞操作1,3和4,显然预测结果与实际情况存在偏差。而采用本文中的预测方法,当采取适当的减速或转向操作时,行人伤害概率出现不同程度的下降,如采取避撞操作2,3,5,6和7,这一点与生活经验更吻合。同时,本文研究的意义在于,通过评估不同避撞操作下的行人伤害概率,结合避撞操作所需的代价,如对驾驶员产生的不适感甚至冲突,乘坐舒适性和本车风险等,为避撞决策提供有效的量化评估手段。

图4 车辆避撞示意图

图5 不同避撞操作下行人伤害预测结果
5 结论
研究了一种考虑行人运动不确定的过街行人碰撞伤害评估方法。行人采用随机行走模型,并应用无味变换预测人-车碰撞概率、碰撞时间与速度的概率密度,在此基础上结合碰撞伤害与速度间的关系,预测行人伤害程度的概率。以MC模拟为参考,分析了本文中方法对碰撞概率和行人伤害预测的准确性。结果表明,本文中方法的预测结果与MC模拟的参考结果基本吻合,并具有较高的计算效率。进一步比较了在各种避撞操作下,确定性方法与本文中方法所预测的行人伤害概率。本文中方法的预测结果反映了各种避撞操作下实际可造成的行人碰撞伤害概率。应用本文中的研究成果,可为行人避撞驾驶辅助系统避撞策略的选择和关键控制参数的确定提供连续而准确的目标量化评估手段。
[1] World Health Organization.Global status report on road safety 2013:Supporting a decade of action[M].Switzerland:World Health Organization,2013.
[2] GANDHI T,TRIVEDI M M.Pedestrian protection systems:Issues, survey, and challenges[J].IEEE Transactions on Intelligent Transportation Systems,2007,8(3):413-430.
[3] COELINGH E,EIDEHALL A,BENGTSSON M.Collision warning with full auto brake and pedestrian detection-a practical example of automatic emergency braking[C].Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems,Sept 19-22,2010, Madeira Island, Portugal.2010:155-160.
[4] 朱西产,刘智超,李霖.基于车辆与行人危险工况的转向避撞控制策略[J].汽车安全与节能学报,2015,6(3):217-223.
[5] KELLER C G,DANG T,FRITZ H,et al.Active pedestrian safety by automatic braking and evasive steering[J].IEEE Transactions on Intelligent Transportation Systems,2011,12(4):1292-1304.
[6] 景超.行人过街交通特性研究[D].长春:吉林大学,2007.
[7] 冯树民,吴阅辛.信号交叉口行人过街速度分析[J].哈尔滨工业大学学报,2004,36(1):76-78.
[8] BRAEUCHLE C,FLEHMIG F,ROSENSTIEL W,et al.Maneuver decision for active pedestrian protection under uncertainty[C].Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems, Oct 6-9,2013, Netherlands,2013:646-651.
[9] MAKRIS D,ELLIS T.Spatial and probabilistic modelling of pedestrian behaviour[C].Proceedings of the BMVC, Sept 2-5, Cardiff, UK,2002:557-566.
[10] KÖHLER S,GOLDHAMMER M,BAUER S,et al.Early detection of the pedestrian’s intention to cross the street[C].Proceedings of the 2012 15th International IEEE Conference on Intelligent Transportation Systems, Sept16-19,IEEE Intelligent Vehicles Symposium,2012:1759-1764.
[11] GOLDHAMMER M,GERHARD M,ZERNETSCH S,et al.Early prediction of a pedestrian’s trajectory at intersections[C].Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems, Oct 6-9,Netherlands,2013:237-242.
[12] KELLER C G,HERMES C,GAVRILA D M.Will the pedestrian cross?probabilistic path prediction based on learned motion features[M].MESTER R,FELSBERG M.Pattern Recognition:33rd DAGM Symposium,Frankfurt/Main,Germany,August 31-September 2, 2011 Proceedings.Berlin, Heidelberg; Springer Berlin Heidelberg,2011:386-395.
[13] NICOLAO G D,FERRARA A,GIACOMINI L.Onboard sensorbased collision risk assessment to improve pedestrians’safety[J].IEEE Transactions on Vehicular Technology,2007,56(5):2405-2413.
[14] SCHUBERT R,RICHTER E,WANIELIK G.Comparison and evaluation of advanced motion models for vehicle tracking[C].Proceedings of the 11th International Conference on Information Fusion, June 30-July 3,2008, IEEE Intelligent Vehicles Symposium,2008:1-6.
[15] JAYANT N.A first-order markov model for understanding delta modulation noise spectra[J].IEEE Transactions on Communications,1978,26(8):1316-1318.
[16] HILLENBRAND J,SPIEKER A,KROSCHEL K.Efficient decision making for a multi-level collision mitigation system[C].Proceedings of the 2006 IEEE Intelligent Vehicles Symposium,June13-15, Tokyo, Japan,2006:460-465.
[17] TAMKE A,DANG T,BREUEL G.A flexible method for criticality assessment in driver assistance systems[C].Proceedings of the Intelligent Vehicles Symposium(IV), June5-9, Baden-Baden,Germany,2011:697-702.
[18] BERTHELOT A,TAMKE A,DANG T,et al.A novel approach for the probabilistic computation of Time-To-Collision[C].Proceedings of the Intelligent Vehicles Symposium(IV),June3-7,IEEE Intelligent Vehicles Symposium,2012:1173-1178.
[19] BERTHELOT A,TAMKE A,DANG T,et al.Handling uncertainties in criticality assessment[C].Proceedings of the Intelligent Vehicles Symposium(IV),June5-9, Baden-Baden,Germany,2011:571-576.
[20] JULIER S J,UHLMANN J K.A general method for approximating nonlinear transformations of probability distributions[R].Technical Report, Robotics Research Group, Department of Engineering Science, University of Oxford,1996.
[21] HANNAWALD L,KAUER F.Equal effectiveness study on pedestrian protection[M].Isaacson:Dresden University of Technology,2004.
[22] KONG C,YANG J.Logistic regression analysis of pedestrian casualty risk in passenger vehicle collisions in China[J].Accident Analysis & Prevention,2010,42(4):987-993.
[23] 黄智,吴乙万,刘剑,等.高速车辆车道偏离辅助控制研究[J].机械工程学报,2013,49(22):157-163.
