半主动悬架系统的最佳阻尼比控制策略研究∗

赵雷雷，周长城，于曰伟

（1.山东理工大学交通与车辆工程学院，淄博 255000； 2.北京邮电大学自动化学院，北京 100876）

前言

传统被动悬架很难满足车辆不同工况下舒适性的需求。为此，设计人员常通过悬架阻尼的控制来改善悬架系统的性能[1－2]。半主动悬架系统因可有效改善车辆行驶舒适性且控制策略的实现比主动悬架成本低，引起了国内外学者的高度关注[3－5]。

目前，国内外学者已对半主动悬架系统阻尼及控制进行了大量研究，应用较多的是基于车身振动速度和基于车身振动加速度的控制方法。其中，应用最多且较成功的控制方法是基于速度控制的天棚控制及其改进方法。虽然采用这两种控制方法的半主动悬架其减振性能都比被动悬架好，但它们并未很好地解决悬架系统的乘坐舒适性和行驶安全性这一对矛盾[6]。国内外学者曾单独以车身振动加速度或车轮动载荷建立目标函数[7]，对悬架系统阻尼匹配进行研究，但所建立的控制方法也未能获得舒适性和安全性的最佳折中。目前，国内外控制领域的学者在半主动悬架方面也做了大量研究工作[8－11]，为提高车辆的乘坐舒适性提供了有益参考。为更全面有效地改善半主动悬架系统的性能，在开发半主动控制策略时须同时考虑悬架性能的多个指标，兼顾车辆乘坐舒适性和行驶安全性要求，建立半主动悬架最佳阻尼比数学模型，并开发相应的半主动控制策略。

本文中通过车辆悬架性能指标的分析，对半主动悬架最佳阻尼比控制策略的数学模型进行探讨；结合实例，对最佳阻尼比控制策略的有效性进行验证。

1 最佳阻尼比控制策略的基本思想

1.1 车辆动力学模型的选取与悬架性能指标

虽然可根据车辆物理模型(图1(a))建立复杂的车辆动力学模型，但在半主动控制策略开发前期，常采用1/4车辆行驶振动模型[6]，如图1(b)所示。

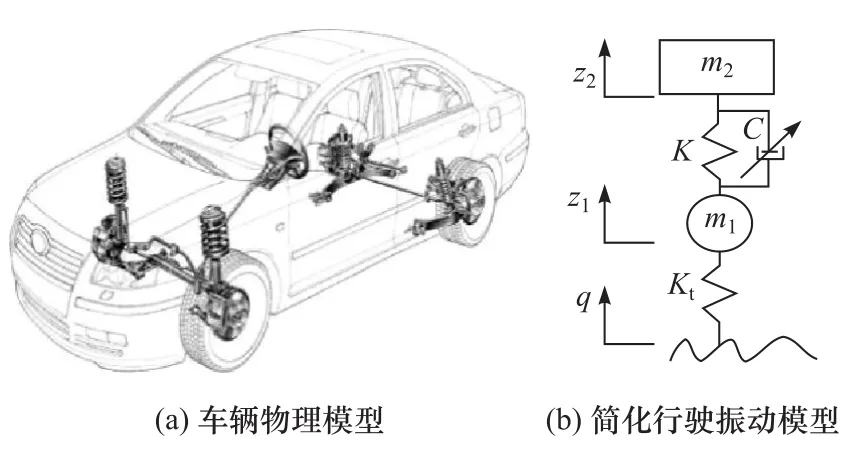
图1 车辆行驶振动模型

其相应的微分方程为

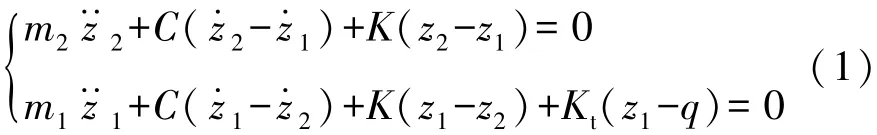
式中:m2，m1分别为单轮簧上、簧下质量；K，Kt分别为悬架及轮胎垂向刚度；C为可调阻尼系数；q为路面输入；z2，z1分别为车轮与车身垂直位移。

为使所讨论物理量具有推广价值，引入以下变量:

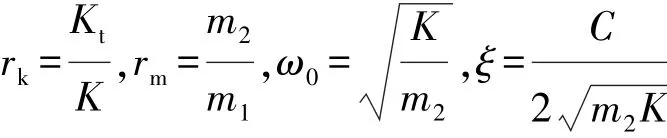
式中:rk为刚度比；rm为质量比；ω0为车身固有圆频率；ξ为悬架系统阻尼比。

为对半主动悬架控制策略的有效性进行全面、合理的评价，目前通常选取车身垂直振动加速度作为舒适性指标，车轮相对动载荷Fd/((m2＋m1)g)作为安全性指标，而以悬架动挠度fd作为辅助评价指标[12]。

1.2 最佳阻尼比控制策略基本思想的提出

为进一步改善悬架性能，提出最佳阻尼比控制策略，其基本思想为:根据不同车速、不同路况调节悬架系统阻尼比ξ，一是可同时满足当前行驶路况对车身振动加速度、车轮动载荷和悬架动挠度3项性能指标的要求；二是相当于根据不同行驶工况在线匹配最佳减振器。

2 半主动悬架最佳阻尼比控制策略

2.1 最佳阻尼比数学模型的构建

由图1(b)所示车辆模型，可得车身垂直振动加速度、车轮动载荷和悬架动挠度的均方响应解析式[12]为

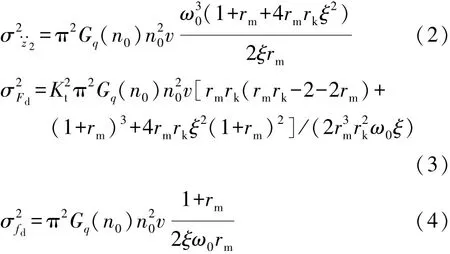
式中:n0为参考空间频率，n0＝0.1m－1；v为车速；Gq(n0)为路面不平度系数。

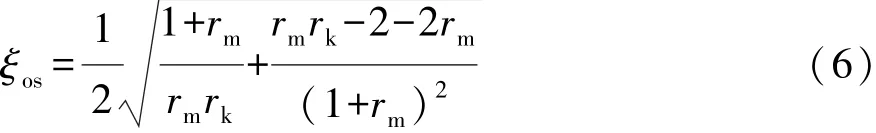
车身加速度、车轮动载荷和悬架动挠度是相互影响和相互制约的。因此，建立无量纲化阻尼比优化目标函数J，并限制悬架撞击限位概率P，则有

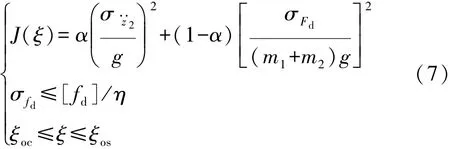
式中:α为加权因子且α∈[0，1]；[fd]为悬架限位行程；η为界限值与标准差的比值，可通过概率分布与标准差的关系确定[12]。

将式(2)～式(4)代入式(7)，由约束条件和阻尼比优化方法所求得的悬架系统最佳阻尼比ξo为

其中

2.2 最佳阻尼比控制策略

由于0≤α≤1，而α取0与1之间的任何数值时，都有 ξoc≤ξ≤ξos，式(8)简化为如下最佳阻尼比ξo控制策略:①当 ξo≤ξoc时，取 ξo＝ξoc；②当 ξo≥ξos时，取 ξo＝ξos；③当 ξoc＜ξo＜ξos时，取 ξo＝ ∇Gq(n0)v。其中，调节度∇＝η2π2n20(1＋rm)/(2ω0rm[fd]2)。 例如，某轿车参数:m2＝340kg，m1＝35kg，K＝20kN/m，Kt＝185kN/m，[fd]＝6.5cm。 限制悬架撞击限位的概率P≤0.3%，此时η＝3.0。最佳阻尼比ξo的控制曲面如图2所示。

图2 不同车速、不同路况下最佳阻尼比ξo的控制曲面

通过分析最佳阻尼比控制策略和图2可知，最佳阻尼比ξo随车速v和路况Gq(n0)而变化，最大值为ξos，最小值为ξoc。汽车在良好路面上行驶时，为保证乘坐舒适性，悬架阻尼比调节为舒适性阻尼比ξoc；在较差路面上行驶时，为保证行驶安全性，悬架阻尼比调节为安全性阻尼比ξos；在中等路面上行驶时，在保证悬架动挠度的前提下，调节阻尼比，使安全性与舒适性达到最好的折中状态。对于实际车辆，悬架结构十分复杂，内部的摩擦阻尼等有时难以用仿真结果反映实际情况，故该控制策略在实际应用时，可根据试验结果对ξoc和ξos进行微调。

3 最佳阻尼比半主动悬架的传递特性

悬架系统各指标的传递特性分析是对悬架特性进行分析的重要方法。根据式(1)和最佳阻尼比控制策略，利用车辆参数 m2＝340kg，m1＝35kg，K＝20kN/m，Kt＝185kN/m，可得半主动悬架系统3项指标对路面随机激励速度q·的传递特性曲面，如图3所示。

根据半主动悬架最佳阻尼比控制策略可知，最佳阻尼比ξo随车速v和路况Gq(n0)而变化。由图3可知，随着最佳阻尼比ξo的变化，悬架系统的3项评价指标的传递特性也改变。因此，在不同车速v和不同路况Gq(n0)下，可根据最佳阻尼比在线匹配最佳减振器性能以满足车辆当前行驶工况的需求。

4 最佳阻尼比控制策略的普适性分析

4.1 悬架限位行程要求对控制策略的影响

车辆在运行过程中，随着行驶速度的增加，阻尼比刚刚要大于舒适性阻尼比时，对应的行驶速度记作最小控制速度v1；当速度继续增加，阻尼比刚刚达到安全性阻尼比时，对应的行驶速度记作最大控制速度v2。根据最佳阻尼比控制策略的原理，可得v1＝ξoc/(∇Gq)且 v2＝ξos/(∇Gq)，控制曲线中斜线段的斜率k＝∇Gq。 例如，某轿车 m2＝340kg，m1＝35kg，K＝20kN/m，Kt＝185kN/m，且要求 P≤0.3%。 当[fd]设计为5.5，6.5和7.5cm时，且该车辆以不同车速v在D级路面上行驶，最佳阻尼比ξo的曲线对比如图4所示。最佳阻尼比ξo控制策略的特征参数如表1所示。其中，可控速度带Δv＝v2－v1。

车辆的悬架限位行程[fd]的设计值越大时，最佳阻尼比ξo的控制曲线对应的最小、最大控制速度v1和v2也越大，且可控速度带Δv也越大，但调节度∇和斜线段斜率k越小，表1和图4清晰地表明了该变化规律。由此可见，在其它车辆参数相同的情况下，[fd]的设计值决定了最佳阻尼比ξo的调节快慢程度。

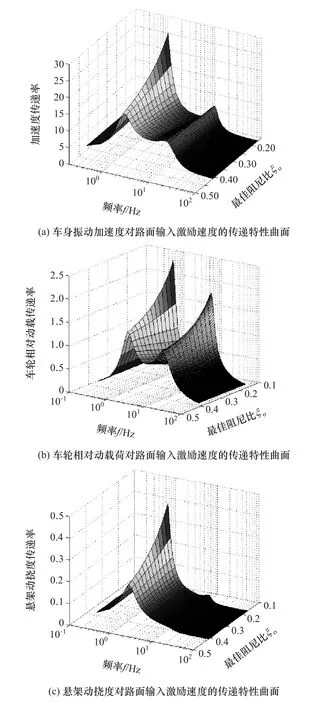
图3 悬架性能指标对路面随机激励速度的传递特性曲面

4.2 悬架撞击限位概率要求对控制策略的影响

为适应不同车辆的开发要求，也可对式(7)中约束条件进行适当调整，即可对所要求的悬架撞击限位概率P进行调整，从而调整最佳阻尼比ξo的特性曲线。例如，某轿车参数 m2＝340kg，m1＝35kg，K＝20kN/m，Kt＝185kN/m，[fd]＝6.5cm。 若根据车辆使用需求，限制悬架撞击限位的概率分别为P≤0.1%，P≤0.3%和P≤1.0%，则该车辆以不同车速v在D级路面上行驶，最佳阻尼比ξo的曲线对比如图5所示。不同概率P下控制策略特征参数的对比如表2所示。

表1 不同悬架限位行程下控制策略特征参数对比

图4 不同悬架限位行程下的最佳阻尼比ξo的控制曲线

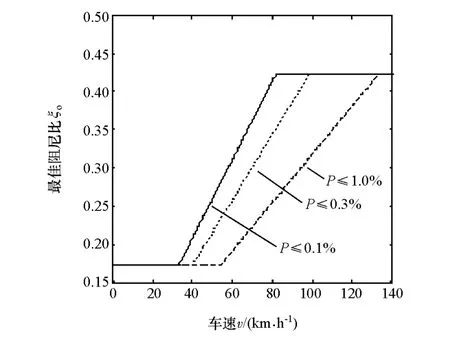
图5 不同悬架撞击限位的概率要求下的最佳阻尼比ξo的控制曲线

由图5和表2可知，限制悬架撞击限位的概率P值越大，最佳阻尼比ξo的控制曲线对应的最小、最大控制速度v1和v2也越大，且可控速度带Δv也越大，但调节度∇和斜线段斜率k越小。由此可见，车辆以不同车速v在同一等级路面上行驶，悬架撞击限位的概率P值和悬架限位行程[fd]的设计值对最佳阻尼比ξo控制策略特征参数的影响规律相似。

表2 不同悬架撞击限位的概率要求下控制策略特征参数对比

5 最佳阻尼比控制策略的有效性分析

在半主动悬架开发前期，先对所提出的控制策略，以被动悬架系统和经典的天棚阻尼半主动控制策略作为参照进行对比仿真分析，进而对最佳阻尼比控制策略的控制效果进行评价。

式中:Cmax＝3000N·s/m，Cmin＝500N·s/m。

5.1 随机路面激励下的时域响应对比分析

随机路面激励下的响应分析是综合考察控制算法的重要手段。文献[13]中的研究设定仿真工况为车辆以72km/h分别在A，B，C和D级路面上行驶，分别考察车辆在被动悬架、天棚阻尼半主动控制和最佳阻尼比半主动控制下悬架3项评价指标的均方根值与最大值。路面时域信号采用滤波白噪声法生成。为充分体现路面的随机特性，仿真时间设为100s，仿真步长设为0.01s，悬架性能评价指标的仿真结果如表3所示。由于篇幅限制，该研究仅给出了B级路况下的时域响应对比，如图6所示。其中，为更清晰地展现各性能指标的变化，图中的时间显示范围为10～14s。

利用Matlab软件的Simulink工具箱，分别建立被动悬架、天棚阻尼控制半主动悬架和最佳阻尼比半主动悬架的控制模型。仿真所用的轿车参数为:m2＝340kg，m1＝ 35kg，K ＝ 20kN/m，Kt＝ 185kN/m，被动悬架阻尼比 ξ＝0.30，[fd]的设计值为65.0mm；P≤0.3%。其中，天棚阻尼半主动控制策略实现方法为[6]

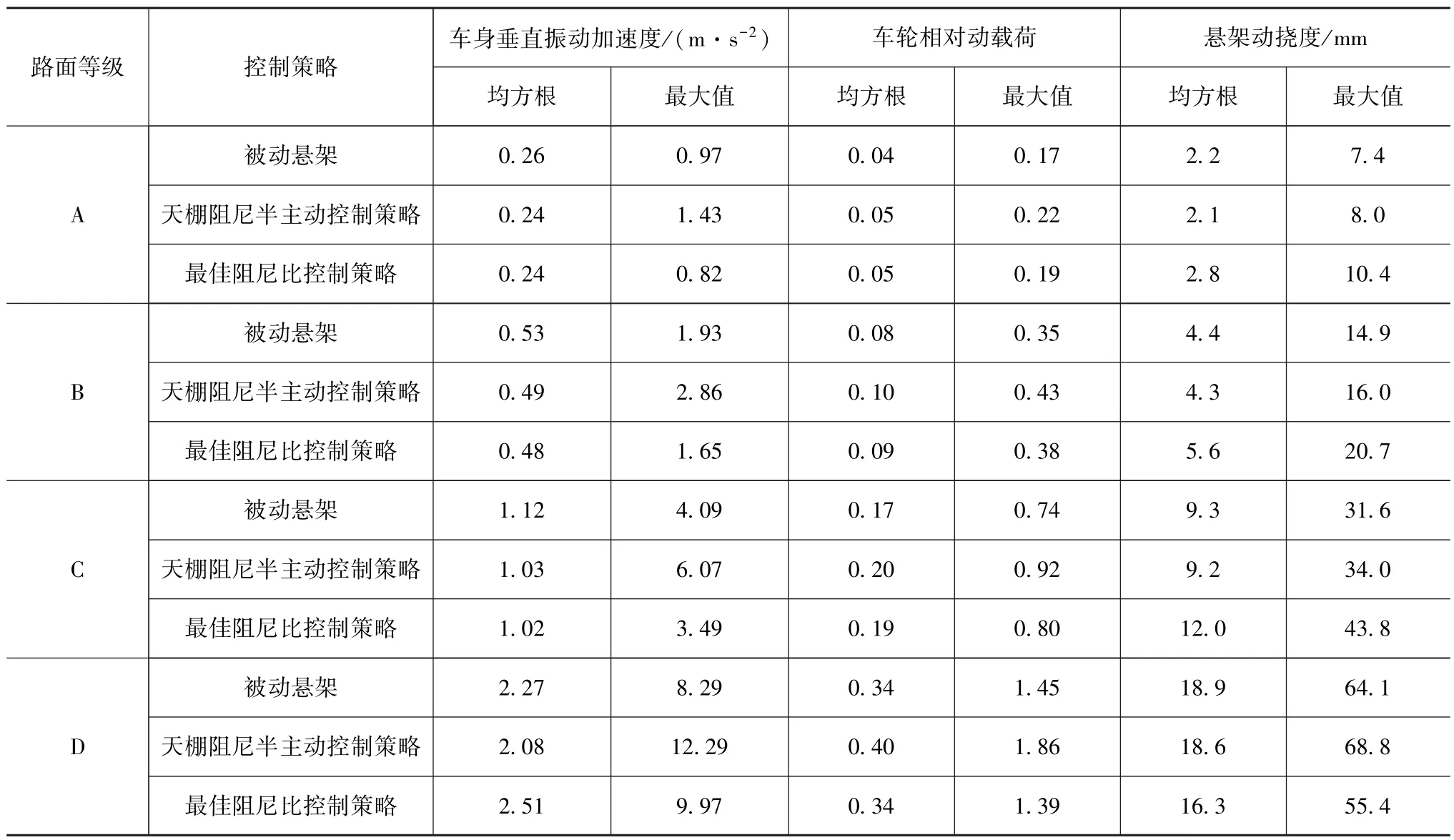
表3 采用不同控制策略的悬架性能评价指标对比

图6 B级路面激励下车辆的时域响应

由表3可知:在较好的路面(A，B，C级)上，最佳阻尼比控制半主动悬架和天棚控制半主动悬架系统的舒适性均优于被动悬架，且两种控制策略对车身垂直振动加速度的抑制效果相当，加速度均方根降低9.0%以上，但在某些时刻，天棚控制策略车身垂直振动加速度出现了明显恶化；与被动悬架相比，两种控制策略均增大了车轮相对动载荷，但在最佳阻尼比控制下，车轮相对动载荷增幅更小；在最佳阻尼比控制下，悬架动挠度均方根值和最大值均略大于被动悬架和天棚半主动悬架，其数值在可接受范围内，且未超出悬架限位行程，这说明最佳阻尼比控制策略更能充分利用悬架设计空间。本文中提出的控制策略在良好路况下主要是以提高车辆的乘坐舒适性为目标，即以降低车身振动加速度为主要目的，故认为达到了预期目的。

由表3还可知:在恶劣路面(D级路面)上，与被动悬架相比，在最佳阻尼比控制策略下，虽然车身垂直振动加速度均方根值增加了8.60%，最大值略有增加，但加速度时域信号变化较平缓，最大值也没有严重恶化，在天棚控制策略下，车身垂直振动加速度降低了9.51%，但最大值依然出现严重恶化现象；与被动悬架相比，天棚控制策略下车轮相对动载荷最大值增大了23.85%，即严重恶化了车轮动载荷，而最佳阻尼比控制策略下车轮相对动载荷最大值降低了7.46%，有效抑制了车轮动载荷，因此，与天棚控制策略相比，最佳阻尼比控制策略能增加车轮的附着能力，提供更好的汽车操纵稳定性和行驶安全性；此外，在天棚控制策略下，悬架动挠度均方根值与被动悬架的相当，但最大值68.8mm超出了悬架限位行程[fd]的设计值65.0mm，这在实际的车辆行驶中将会增加撞击限位的概率而使舒适性变差，而在最佳阻尼比控制策略下，悬架动挠度均方根值比被动悬架减小了13.76%，且最大值55.4mm也未超出限位行程，由此可见，在恶劣路况下，最佳阻尼比控制策略能有效避免撞击现象。

5.2 随机路面激励下的频谱对比分析

为进一步说明恶劣路况下最佳阻尼比控制策略的有效性，对D级路况下悬架各性能指标在0～30Hz进行功率谱密度分析，结果如图7所示。

由图7(a)可知:与被动悬架相比，天棚阻尼控制策略在低频区明显改善了车辆乘坐舒适性，但在中高频区减振效果不明显，甚至使舒适性恶化；而最佳阻尼比控制策略能在低频共振区有效抑制车身振动，在中频区舒适性略有降低，高频区与被动悬架相当。由图7(b)可知，与被动悬架相比，天棚阻尼控制策略仅在低频共振区有效抑制车轮动载荷，而最佳阻尼比控制策略在低频和高频共振区都能有效抑制车轮动载荷。由图7(c)可知，与被动悬架相比，天棚阻尼控制策略在低频段增大了悬架动挠度，在中高频段对悬架动挠度的改善不明显，而最佳阻尼比控制策略有效抑制了悬架动挠度的低频和高频共振峰值。综合图7(a)～图7(c)可知，最佳阻尼比控制策略降低了车身垂直振动加速度在低频共振区的峰值，车轮动载荷和悬架弹簧动挠度在低频及高频共振区的峰值也得到了明显改善。该控制策略在恶劣路况下主要是以提高车辆的越野性能为目标，即以降低车轮相对动载荷并减小限位块撞击概率为主要目的，故认为达到了预期目的。

6 结论

图7 车轮相对动载荷的幅频特性

提出了一种半主动悬架系统的最佳阻尼比控制策略。基于车辆行驶振动模型，利用在随机路谱下车身垂直振动加速度、车轮动载荷和悬架动挠度均方响应，创建了半主动悬架系统最佳阻尼比控制策略的数学表达式；对半主动悬架系统的传递特性进了行分析。通过实例，对控制策略进行了对比研究，结果表明:最佳阻尼比控制策略是有效的，为汽车半主动悬架控制提供了有益参考。

[1] MACIEJEWSKI I， KICZKOWIAK T， KRZYZYNSKI T.Application of the Pareto-optimal approach for selecting dynamic characteristics of seat suspension systems[J].Vehicle System Dynamics，2011，49(12):1929－1950.

[2] BREZAS P，SMITHA M C，HOULT W.A clipped-optimal control algorithm for semi-active vehicle suspensions:Theory and experimental evaluation[J].Automatica，2015，53:188－194.

[3] LEE C M，GOVERDOVSKIY V N，TEMNIKOV A I.Design of springs with “negative” stiffness to improve vehicle driver vibration isolation[J].Journal of Sound and Vibration，2007，302:865－874.[4] JAMALI A，SHAMS H，FASIHOZAMAN M.Pareto multi-objective optimum design of vehicle-suspension system under random road excitations[J].Proceedings of the Institution of Mechanical Engineers Part K-Journal of Multi-body Dynamics，2014，228(3):282－293.

[5] 高瑞贞，张京军，赵子月，等.基于改进遗传算法的半主动悬架系统模糊控制优化研究[J].工程力学，2012，29(1):240－248.

[6] 张磊，张进秋，彭志召，等.车辆半主动悬架改进型天棚阻尼控制算法[J].汽车工程，2015，37(8):931－935.

[7] QAZI A J， FAROOQUI U A， KHAN A， et al.Optimization of semi-active suspension system using particle swarm optimization algorithm[J].AASRI Procedia，2013，4:160－166.

[8] 朱跃，朱思洪，肖茂华.座椅悬架不匹配干扰估计全程滑模控制研究[J].振动工程学报，2014，27(5):654－660.

[9] NGUYEN S D，NGUYEN Q H，CHOI S B.A hybrid clustering based fuzzy structure for vibration control－part 2:an application to semi-active vehicle seat-suspension system[J].Mechanical Systems and Signal Processing，2015，56:288－301.

[10] 王其东，王祺明，陈无畏.磁流变半主动悬架变论域模糊控制研究[J].振动工程学报，2009，22(5):512－518.

[11] UNGER A，SCHIMMACK F，LOHMANN B，et al.Application of LQ-based semi-active suspension control in a vehicle[J].Control Engineering Practice，2013，21:1841－1850.

[12] 周长城.汽车平顺性与悬架系统设计[M].北京:机械工业出版社，2011.

[13] 陈杰平，陈无畏，祝辉，等.基于Matlab/Simulink的随机路面建模与不平度仿真[J].农业机械学报，2010，41(3):12－15.