基于分形统计测度的投资组合研究

，，，

(1.成都理工大学商学院，成都 610059；2.广州大学经济与统计学院，广州 510006)

0 引言

现代投资组合理论(Modern Portfolio Theory, MTP)自创立至今已有60余年[1]。MTP研究的核心问题是投资者如何通过构建投资组合将资金分散地投资于不同资产实现分散风险和确保收益。MTP既是现代金融学的开端，也是现代金融理论研究的动力，在金融理论研究和金融实务操作中均占据着重要的地位。目前，已有大量学者对MTP进行了研究，并取得了一些成果[2-5]。虽然这些成果丰富了MTP，但是现有成果在构建投资组合时主要使用均值、方差、下偏方差、模糊数学、条件在险价值、集成预测熵等方法来测量证券的收益和风险[4-6]。在证券价格没有分形特征时，使用均值、方差、下偏方差、模糊数学等方法也许能够准确地测量出证券的收益和风险。然而，大量研究表明证券价格普遍具有明显的分形特征[7-11]，如：有学者实证发现衍生品和现货市场都具有分形特征[7]，有学者实证发现上海和深圳股票市场均有多重分形特征[9-10]，还有学者实证发现32个国家的股票指数均具有分形特征[11]。此时，使用这些方法测量证券的收益和风险便存在难以准确测量甚至无法测量的缺陷[12-14]。

具体而言，当证券价格具有分形特征时，证券价格波动服从分形布朗运动，证券收益率服从分形分布，表现出自相似性、标度不变性、长记性等特征，呈现出无穷精细的复杂结构[11-15]。已有学者明确指出，对于价格具有分形特征的证券，分形方法是刻画其特征的有力工具[13-14]；随后，大量学者的研究表明，当正确价格具有分形特征时，只有使用分形方法来测量证券的收益和风险等特征，所得到的结果才可能准确；采用均值、方差、下偏方差、模糊数学等非分形方法难以将证券的收益和风险等特征准确测量[15-18]。同时，根据前文可知，当证券价格具有分形特征时证券收益率服从分形分布。分形分布是较为复杂的幂率分布，其均值和方差可能趋于无限[19-20]；此时，采用均值、方差、下偏方差等非分形方法来测量证券的收益和风险便面临着无法测量的可能[21]。可见，现有研究主要使用非分形方法来测量证券的收益和风险存在测不准或不可测的缺陷，最终导致所构建的投资组合缺乏有效性。

综上可见，研究MTP具有重要的理论和应用价值，现有相关成果在测量证券收益和风险时使用的方法主要属于非分形方法，在证券价格普遍存在分形特征的现实背景下，存在测不准或不可测的缺陷，影响投资组合的有效性。基于此，本文首先构建了分形期望和分形方差两个分形统计测度来测量证券的收益和风险；其次，以分形统计测度为基础构建了分形组合模型，给出了分形组合模型的解析解，最后，实证分析了分形组合模型的有效性。

1 分形统计测度构建

针对使用期望和方差等非分形方法来测量证券的收益和风险存在测不准或不可测的缺陷，本文借鉴分形观点下处理曲线长度的方法来构建分形期望和分形方差两个分形统计测度，以便在证券价格普遍具有分形特征的现实背景下较为准确地测量证券的收益和风险。

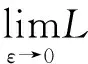
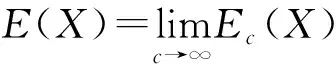
(1)

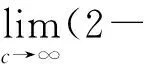
(2)

(3)

(4)

(5)

(6)

(7)

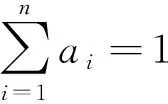
(8)

综上，本文构建了分形期望和分形方差两个分形统计测度，并给出了两个分形统计测度的运算规则，为进一步阐述基于分形统计测度构建投资组合中奠定了基础。

2 分形统计测度下的组合模型

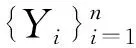
(9)

(10)

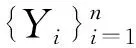
(11)

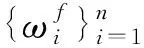
(12)

(13)

(14)

由上可见，前文所构建的两个分形统计测度，不仅在理论上可以构建投资组合，还可将数组权重转换为数值权重，应用于投资实践。从而，完整地解决了分形统计测度下的投资组合问题。为了表述的方便，下文将基于分形期望和分形方差两个分形统计测度所构建的投资组合模型简称为分形组合。

3 分形组合的有效性分析

在理论模型构建的基础上，便可利用实证分析来验证分形组合的有效性。在既定收益水平约束下，如果分形组合的风险小于基准组合的风险，则表明分形组合有效。在基准组合的选取上，考虑到分形组合较之Markowitz传统组合模型主要是在风险和收益测度上进行改进；因此本文以Markowitz传统组合模型作为基准组合。在样本选取上，本文以上海证券交易所的所有6种行业指数为资产样本，并分别用传统期望和方差、分形期望与方差计算其风险与收益来构建基准组合与分形组合。在样本区间选取上，为了反映分形组合在不同市场行情下的效果，以2012年1月1日至2017年1月1日为整个样本区间，并以每一年为子区间构建组合观察所构建的组合的风险情况。数据来源于聚源数据库。

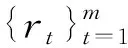
表1 30个密度函数的两个参数和拟合优度Tab.1 Two parameters and fit goodness for 30 density functions

由表1可知，30个资产收益率序列的拟合优度最低为0.798，且回归方程的拟合优度大多在0.9以上；从而说明收益率序列的密度函数确实为幂率形式，表1所示的30个密度函数的两个参数具有较高的可靠性。根据表1的结果，利用(2)和式(6)便可计算出30个收益率序列的分形期望和分形方差，见下表2；限于篇幅，表2仅罗列了数值，未罗列数组符号。

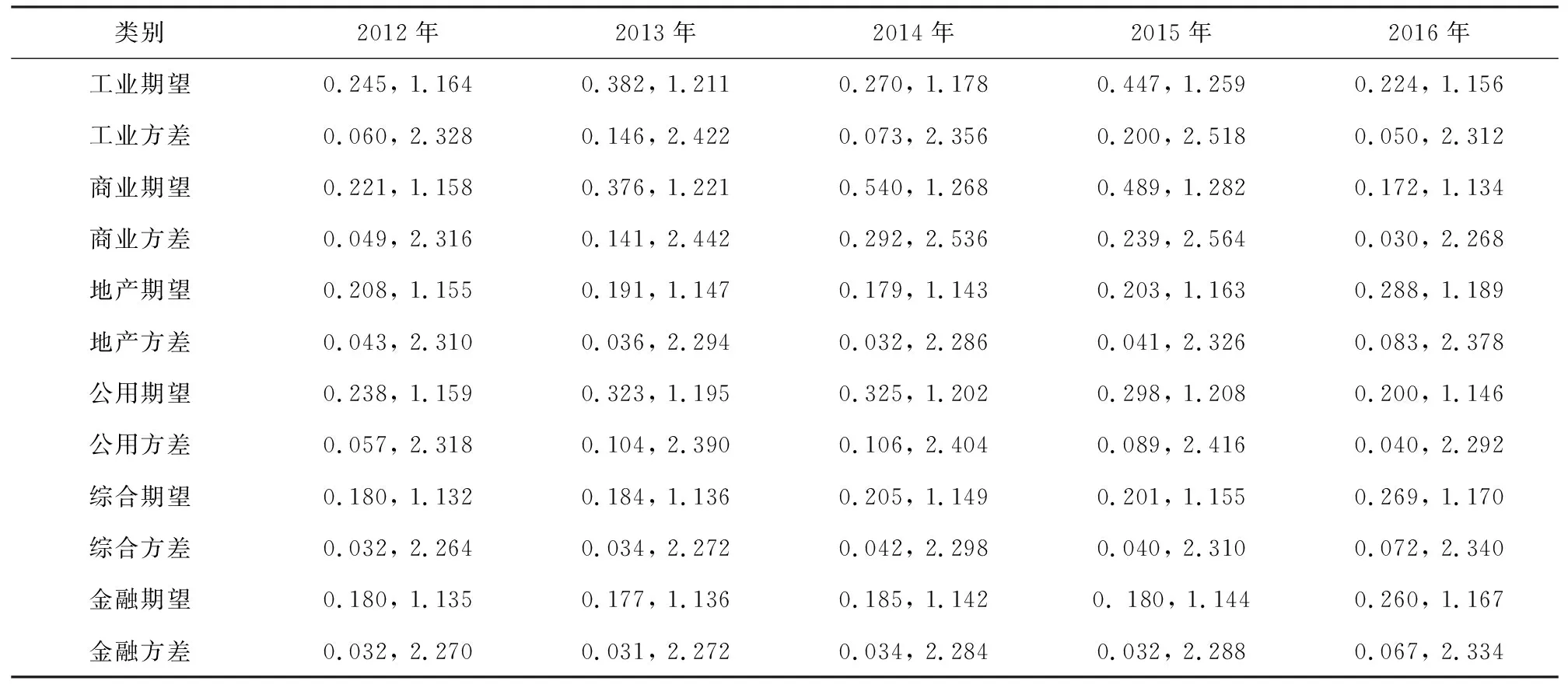
表2 30个收益率序列的分形期望和分形方差Tab.2 Fractal expectation and fractal variance of 30 yield series

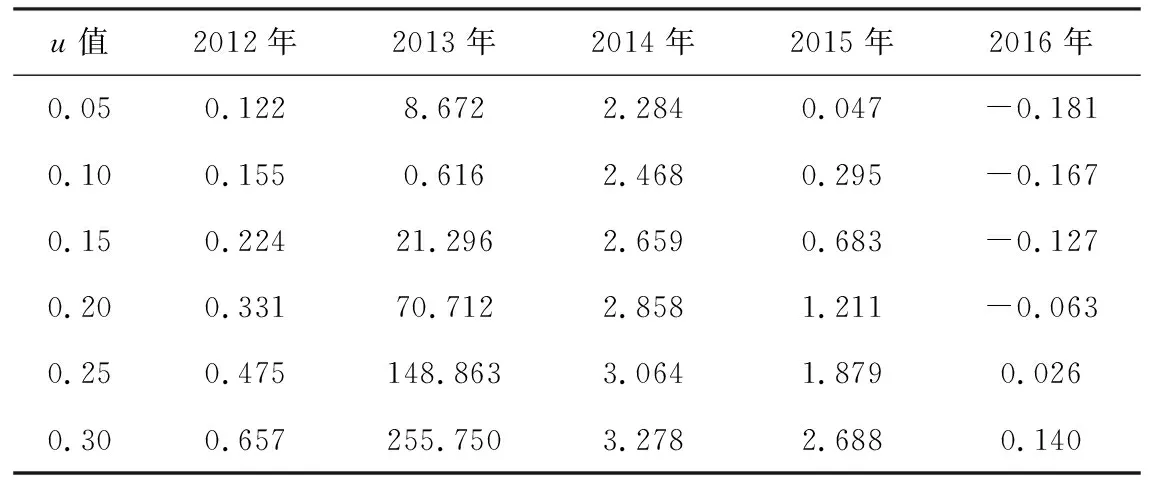
表3 既定收益下基准与分形组合的风险之差Tab.3 The difference between benchmark and fractal portfolio under defined returns

注：表中数据的单位为0.001。

在表2的基础上，利用式(14)便可计算出分形组合中各资产的投资权重，进而获得分形组合的风险。同理，根据30个收益率序列的传统期望和传统方差，利用式(10)便可计算出基准组合中各资产的投资权重，进而获得基准组合的风险。便于比较，如下表3将6种既定收益水平下基准组合和分形组合的风险之差进行罗列。

由表3可知，在所有30种情形中，基准与分形风险资产组合的风险之差有26种情形为正值，即在既定收益水平下，有26种分形风险资产组合的风险都小于基准风险资产组合的风险，占比86.67%。因此，在既定收益下，分形组合的风险大多小于基准组合的风险，分形组合在确保收益的同时更好地分散了风险。综上可见，本文构建的两个分形统计测度可以用于构建投资组合，且基于分形统计测度所构建的分形组合具有有效性。

4 结论与展望

本文基于分形理论构建了分形期望和分形方差两个分形统计测度，以克服非分形统计测度难以准确测量甚至无法测量证券风险与收益的缺陷。在此基础上，基于分形统计测度构建了分形组合模型，并给出了模型的解析解。随后，通过比较分形组合与传统投资组合的风险情况，从实证分析的视角验证了分形组合的有效性。尽管本文基于分形理论开创性地构建了分形期望和分形方差两个分形统计测度，并构建了分形组合，但本文的研究仍属于探索性研究；因此，无论是在一般形式的分形分布下构建分形期望和分形方差，还是高阶矩分形统计测度的构建探究，无论是含有背景风险的分形组合探讨，还是多阶段动态分形组合的探索，都有待深化。