加权网络的体积维数
2018-02-28,,,,
, ,, ,
(南昌航空大学信息工程学院,南昌 330063)
0 引言
复杂网络作为复杂系统的高度抽象和研究工具,近十几年来受到了来自计算机科学、信息科学、生物学、统计物理学、社会学等众多不同学科领域研究人员的广泛关注,成为科学研究的热点。对复杂网络拓扑性质的准确度量对于复杂网络模型的建立以及复杂网络动力学行为的研究具有十分重要的意义,因此复杂网络拓扑性质的研究也是复杂网络理论研究的关键。20世纪末,科学家们揭示了复杂网络的两大基本拓扑特性:小世界特性和无标度特性[1-2]。小世界特性是指网络节点间的平均路径短且平均聚集系数高,对应于社交网络中的“六度分割”现象。无标度特性则是指网络节点的度分布服从幂律分布,对应于经济生活中的“马太效应”。随后,2005年, Song等人开创性地将重整化理论和分形理论中的盒子覆盖法推广应用于复杂网络的研究,揭示了大量实际网络具有自相似性和分形特性[3],其中自相似性是指网络度分布的幂律形式及幂指数在重整化过程中保持不变,分形特性则是指覆盖整个网络所需的最小盒子数量与盒子长度呈幂律关系,即NB(lB)≈lB-dB,dB为网络的分形维数。复杂网络分形特性的揭示有助于人们更加深入地理解网络结构的复杂性。同时,分形特性也被誉为复杂网络的第三大基本拓扑特性。
分形维数是定量刻画分形体分形特性的最重要指标。在复杂网络领域,关于分形维数的定义和算法有很多[4-6],其中最常见的是由盒子覆盖法定义的盒维数[7]。盒子覆盖法计算网络盒维数的过程大致可分为3个步骤:第一步用长度为lB的盒子覆盖整个网络(一个盒子就是一组节点的集合,在此集合中任意两个节点间的距离小于lB),计算覆盖整个网络所需的最小盒子数量NB(lB);第二步增加盒子长度lB(每次以1递增,直到lB等于网络的直径),分别计算在规定盒子长度下所需的最小盒子数量NB(lB);第三步将数据对(lB,NB(lB))绘制在双对数坐标中,若lB与NB(lB)呈幂律关系,则表明网络具有分形特性,盒维数即为拟合直线斜率的绝对值。实质上,盒子覆盖法可归结为如何在规定的盒子长度下找到覆盖整个网络所需的最小盒子数量,这是一个NP完全问题,只能尽可能找到最优解。Song等人在文献[8]中提出了3种经典的方法:贪婪着色算法、紧凑盒子燃烧算法以及最大排除质量燃烧算法。随后,更多的改进盒子覆盖算法被提出。例如Schneider等人在最大排除质量燃烧算法的基础上,提出了一种新型的优化算法[9],该算法在对许多实际网络的分形分析中能得到更加精确的解,但是该算法的时间复杂度较高,达到O(2N),N为网络节点总数。Sun等人提出了重叠盒子覆盖算法[10],这种可重叠盒子的思想与现实网络存在重叠社区是相吻合的,并且该算法能得到与Schneider等人提出的算法相媲美的结果。 此外,也有不少研究人员根据网络的现实特征从其他角度提出了一些盒子覆盖算法。例如Zhang等人[11]利用网络节点间的排斥力重新定义了节点间的距离,也可以得到现实网络的分形特征。Wu等人[12]将最小化盒子数量与最大化分形模块度作为盒覆盖过程中的优化目标,提出了一种多目标优化的盒子覆盖法。Wei等人[13]考虑到现实中的网络多为加权网络而传统的盒子覆盖算法并不完全适用于度量加权网络的分形特性,从而提出了一种加权的盒子覆盖算法,为分析加权网络的分形特性提供了新的视角和方法。
除盒子覆盖法定义的盒维数外,体积维数也被广泛地应用于度量网络的分形特性。值得注意的是,这里所指的“体积”与传统意义上三维空间中的体积并非一个概念。复杂网络体积维数的概念最早由O.Shanker提出[14-15], 其基本思想为任选节点i为中心节点,将半径r范围内覆盖到的节点数量定义为节点i的体积,然后遍历网络中的节点为中心节点,计算所有节点的体积和的平均值,记为V(r),通过改变r的取值,多次实验后若V(r)与r满足幂律关系V(r)~rdv,则说明网络具有分形特性,其中dv为对应的体积维数。随后,Guo等人[16]及Wei等人[17]进一步改进了O.Shanker提出的体积维数的概念,并用改进后的方法分析了多个实际网络的分形特性。然而,现有的网络分形维数的定义主要是针对无权网络提出,鲜有关于加权网络分形维数的定义及算法。加权网络和无权网络相比能对复杂系统各单元间的关系及相互作用提供更加细致的刻画。因此,完善有关加权网络的分形研究理论有助于去分析实际加权网络中的统计特性从而更好地认识复杂系统。在O.Shanker提出的无权网络体积维数中,在尺度r(半径)下,每个节点的体积为以该节点为中心覆盖到的节点数目,整个网络的体积则为所有节点体积的平均值,也即O.Shanker是以节点数目来定义网络的“体积”。加权网络中,节点的强度是一个非常重要的统计量,其是节点局域信息的一种综合表达方式[18]。因此,本文沿着O.Shanker提出的无权网络体积维数思想进一步考虑,在尺度r(半径)下,将每个节点的体积定义为以该节点为中心节点覆盖到的节点强度和,将整个网络的“体积”定义为所有节点体积的平均值,从强度体积的角度来考察加权网络的分形特征,并称这种衡量加权网络分形特性的维数为强度体积维。
1 前期工作
一个给定的复杂网络可以抽象为一个由点集V和边集E组成的图G=(V,E),其中E中的每条边都有V中的一对节点与之对应。无权网络中任意两个节点间的距离定义为连接这两个节点的最小边数,因此其值为正整数。在O.Shanker提出的经典的体积维数定义中,“体积”是指每一盒子长度下覆盖到的节点的数量。Guo等人将O.Shanker提出的体积维数进行了进一步改进:首先任选节点i为中心节点并设定盒子长度为r, 将r范围内覆盖到的节点数量与网络节点总数间的比值定义为节点i的密度,然后遍历网络中的所有节点为中心节点,计算得到给定盒子长度r下的平均密度,记为〈ρ(r)〉,通过对一些实际无权网络的实证分析,Guo等人发现〈ρ(r)〉与r之间存在一定的幂律关系[16]:
〈ρ(r)〉≃krdf
(1)
其中,k为实数,df为网络的体积维数。Guo等人是从网络密度〈ρ(r)〉和测量尺度之间的幂律关系来考察网络的分形特征,本质上,〈ρ(r)〉反应的是特定长度的盒子对网络的一种覆盖能力。Wei等人[17]则将每一盒子长度下覆盖到的节点度和的平均值作为考察对象,从度体积的角度研究了无权网络的分形特性,发现无权分形网络存在如下关系式:
VD(r)≃kdrdd
(2)
其中,VD(r)表示盒子半径为r时所覆盖到的节点的度和平均值,kd为常数值,dd为体积维数。这些不同的方法从不同的角度度量了无权网络的分形特性。并且,盒长r的赋值规则均是从1开始逐次加1直到等于网络的直径。
2 基于节点强度的加权网络体积维数
2.1 算法思想
在加权网络中,节点的强度是一个基础但十分重要的统计量。网络中任一节点i的强度可由式(3)计算[19-20]
(3)
其中,Ni为节点i的邻居节点的集合,wij为连接节点i和节点j的边的权重值。节点的强度既包含了节点度的信息也包含了与该节点相连的边权的信息,是节点局域信息的一种综合表达方式。并且,不同强度值的节点也体现了网络节点间的差异性。
和无权网络相比,加权网络最突出的特点是连边强度的异质性,而正是这种异质性使得加权网络中任意两个节点间的距离定义与无权网络中不一致。目前如何通过网络权重值来计算节点间的距离并无统一的标准,最常用的方法是Dijkstra算法,具体描述为
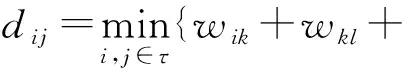
(4)
或者是
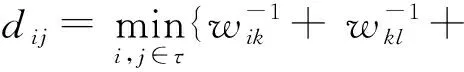
(5)
其中,τ为节点i和节点j之间所有相连路径的集合。式(4)表示网络权重为相异权的情况,式(5)表示网络权重为相似权的情况。但是,由式(4)或式(5)计算出的节点间距离值通常较小,表明网络的直径也很小,甚至有些实际加权网络的直径小于1。这说明当盒长设置为1时即可将网络中的所有的节点覆盖,因此针对无权网络的盒子长度赋值规则并不完全适用于加权网络。文献[13]提出的针对加权网络的盒子长度赋值规则能很好地解决这一问题,其核心思想是摒弃习惯上盒子长度为整数的想法,通过对直接相连的节点间距离值进行累加来给盒子长度赋值。受这种思想的启发,本文以不同盒长r下覆盖到的节点强度和来定义加权网络体积维中“体积”的概念,从强度体积的角度来考察加权网络的分形特性。
2.2 算法步骤
按照强度体积维的定义,算法设计如下:
步骤1对给定的加权复杂网络G,根据网络权重值表示的实际含义,计算网络中直接相连的节点间的距离值,并按从小到大的顺序排序,记为d1,d2,d3,…dn,设置初始盒长r=d1。
步骤2计算G中所有节点的强度值。
步骤3随机选择节点i为中心节点,计算到节点i的距离小于r的所有节点的强度和,记为ViS(r)。
步骤4遍历网络中的所有节点,计算节点强度和的平均值,记为VS,数值上有:
(6)
步骤5分别设置盒子长度r=d1+d2,r=d1+d2+d3,r=d1+d2+d3+…dn,重复步骤3和4,直到r大于网络的直径,统计出每个r所对应的VS(r)。
步骤6拟合lnVS(r)~lnr的直线,直线的斜率值即为强度体积维数值ds。
3 实验结果及分析
本节分别利用强度体积维数来度量两类构造的加权网络的分形特性及3个实际加权网络的分形特性。并在对实际网络的分形分析中,将分析结果与利用盒维数得到的结果进行对比。
3.1 对构造网络的分析
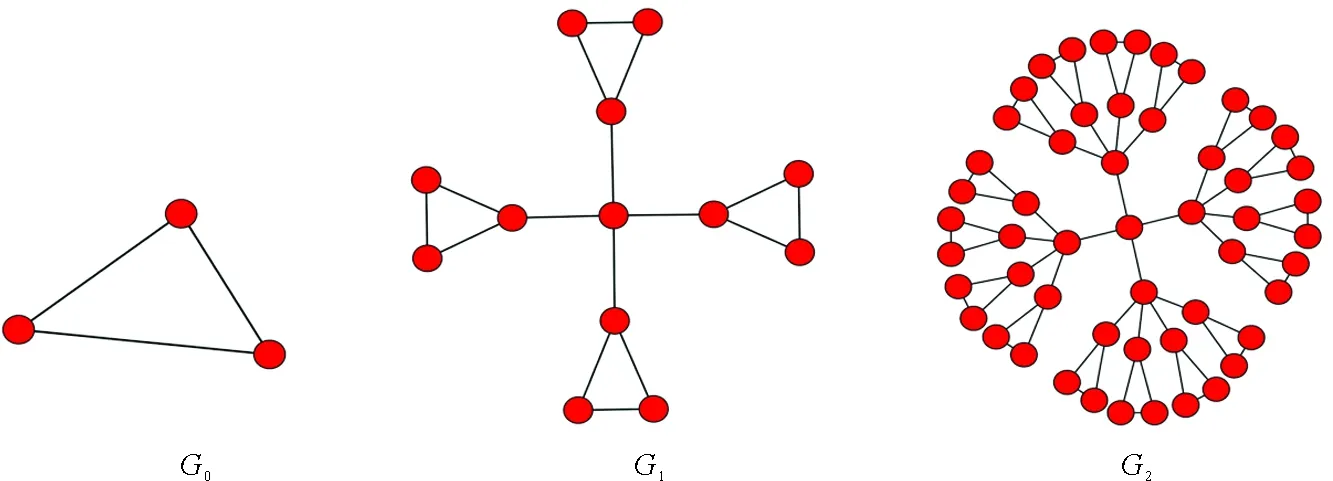
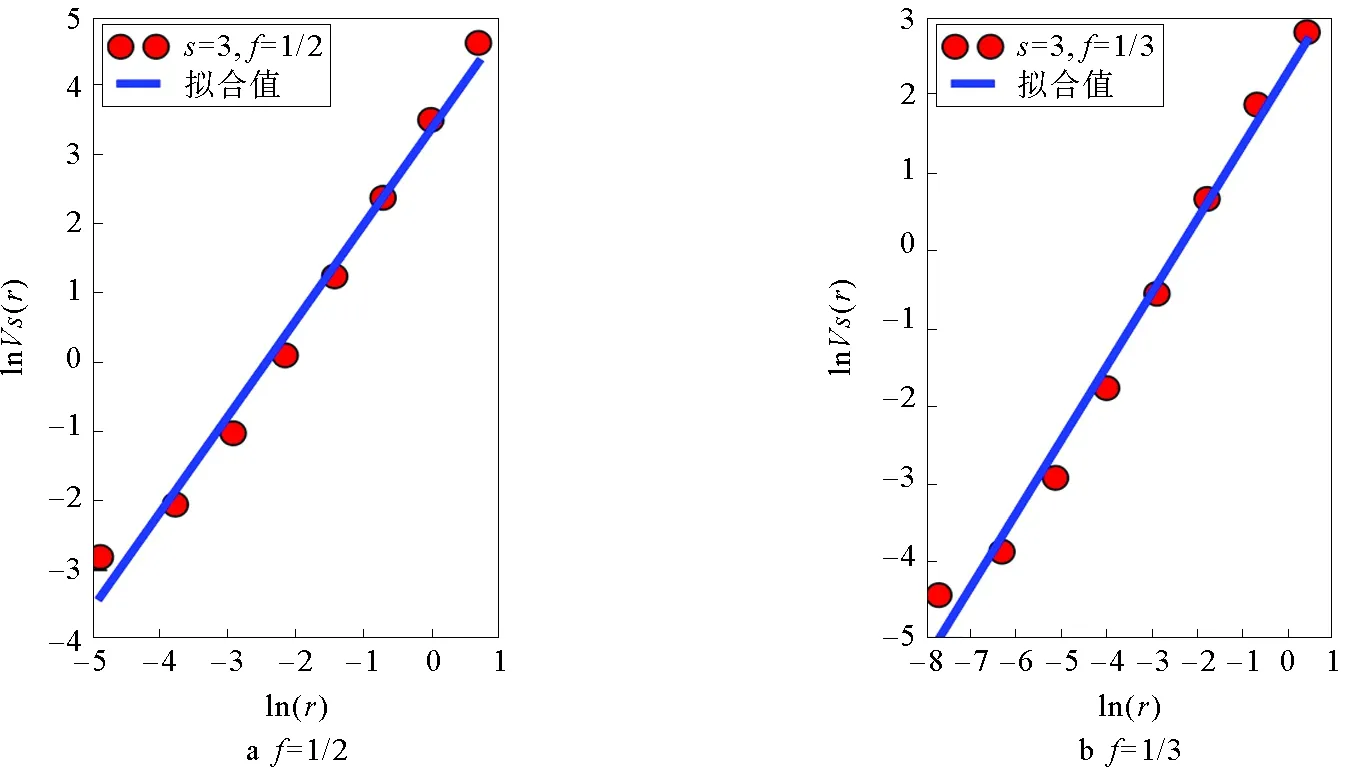
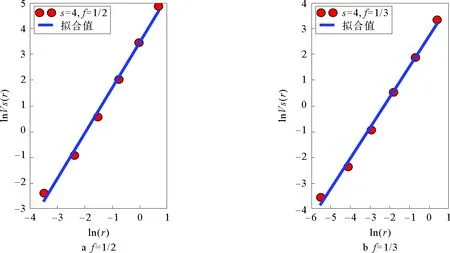
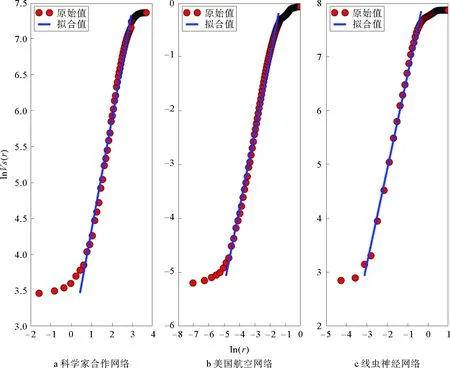
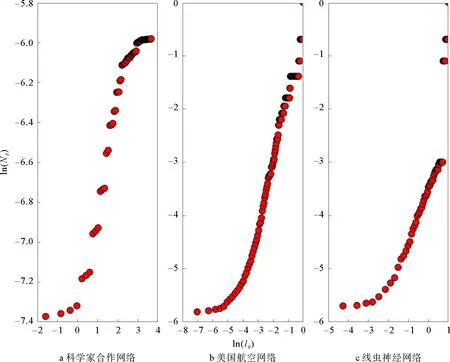
谢尔宾斯基加权分形网络和康托三角尘加权分形网络是由Carletti等人提出[21],由迭代函数系统(Iterated Function Systems)生成。这两类网络的生成过程和自相似维数(也称豪斯多夫维数)由两个主要的参数决定,分别是图形复制数目s(s>1)以及变化比例因子f(0 (7) 为了构造谢尔宾斯基加权分形网络,初始网络设置为单个节点,然后根据参数s和f的值依次生成下一代网络。如图1表示s=3,f=1/2的谢尔宾斯基加权网络的生成过程,其中G0由单个节点构成,将G0复制三次并用一个新的节点通过权重值为“1”的边连接起来得到G1,如此重复,后一次的边权重值变为前一次的“1/2”,易知其自相似维数为lg3/lg2≈1.585 0。康托三角尘加权分形网络的生成过程与此类似。如图2表示s=4,f=1/5的康托三角尘加权分形网络的生成过程,其中初始网络G0由一个三角形组成,将G0复制4次然后用一个新的节点通过权重值为“1”的边连接起来得到G1,如此重复,后一次的边权重值变为前一次的“1/5”,易知其自相似维数为lg4/lg5≈0.861 3。 s=3,f=1/2图1 谢尔宾斯基加权网络生成过程Fig.1 The growth process of Sierpinski weighted networks s=4,f=1/5图2 康托三角尘加权网络生成过程Fig.2 The growth process of Cantor dust weighted networks 对于谢尔宾斯基加权网络,首先考虑s=3,f=1/2和s=3,f=1/3两种情况。考虑到计算机处理能力有限,这里只生成第八代谢尔宾斯基加权网络,记为G8。G8具有9 841个节点和9 837条边。当s=3,f=1/2时,边的权重值分为1 ,1/2, 1/4, 1/8, 1/16,1/32,1/64,1/128八类,当s=3,f=1/3时,边的权重值分为1, 1/3, 1/9,1/27,1/81, 1/243,1/729,1/2 187八类。由于谢尔宾斯基加权网络的边权重值并无特殊的物理含义,因此可直接将边权重值视为连接这两个节点的距离值。当s=3,f=1/2时,分别设置盒子长度r为1/128, 1/128+1/64,…,1/128+1/64+1/32+1/16+1/8+1/4+1/2+1,然后计算相应盒子长度下节点强度和的平均值VS(r),结果如图3a所示。同理设置s=3,f=1/3时的盒子长度并计算相应盒子长度下节点强度和的平均值,结果如图3b所示。 对于康托三角尘加权网络,这里只生成第六代网络,其具有13 653个节点和17 748条边。类似地,首先考虑s=4,f=1/2和s=4,f=1/3两种情况,结果分别如图4a和图4b所示。 s=3图3 第八代谢尔宾斯基加权网络的分形特性分析Fig.3 The fractal property analysis of the eighth generation of Sierpinski weighted networks s=4图4 第六代康托三角尘加权网络的分形特性分析Fig.4 The fractal property analysis of the sixth generation of Cantor dust weighted networks 从图3和图4可以看出,无论是谢尔宾斯基加权网络还是康托三角尘加权网络,两种情况下盒子长度与相应的节点强度和的平均值均能很好地拟合成一条直线。谢尔宾斯基加权网络拟合直线的斜率值分别为1.398和0.946,与理论计算的自相似维数值1.585 0和1相差不大。康托三角尘加权网络拟合直线的斜率值分别为1.764和1.181,同样与理论计算的自相似维数值2和1.262相差不大。这初步表明了强度体积维数在加权网络分形分析上的有效性。 为了进一步验证强度体积维数的有效性,在谢尔宾斯基加权网络中,令图形复制数目s=3,然后分别设置变化比例因子f=1/4,1/5,1/6,1/7,1/8,1/9,计算对应的强度体积维数值,并与理论值进行比较。在康托三角尘加权网络中,令图形复制数目s=4,然后分别设置变化比例因子f=1/4,1/5,1/6,1/7,1/8,1/9,计算对应的强度体积维数值,并与理论值进行比较。结果如表1和表2所示。 表1 s=3时,不同f值的谢尔宾斯基网络对应的强度体积维数与理论维数Tab.1 The volume dimensions and the theoretical dimensions of Sierpinski weighted networks with s=3 and different values of f 表2 s=4时,不同f值的康托三角尘网络对应的强度体积维数与理论维数Tab.2 The volume dimensions and the theoretical dimensions of Cantor dust weighted networks with s=3 and different values of f 从表1和表2可以看出,当变化比例因子f取不同值时,谢尔宾斯基加权网络和康托三角尘加权网络的强度体积维数值与理论计算的维数值十分接近,这充分说明了强度体积维数在分析构造加权网络分形特性时的有效性。强度体积维数和理论的分形维数在数值上并不会严格相等,这是因为二者具有不同的定义,是从两个不同的角度对同一个分形体的分形特征进行考察。而不同定义的分形维数具有的性质差别可能很大,即使是对很“规则”的分形体,不同定义的分形维数也不能给出相同的维数值[22],这也是强度体积维数和理论分形维数在数值结果上不会严格相等的重要原因。 对构造加权网络的分形分析结果表明了强度体积维数的有效性,进一步地,利用强度体积维数分析3个更具代表性的实际加权网络的分形特性。为对照研究,这里选取与文献[13]中一致的网络数据,分别是Newman科学家合作网络[23],美国航空网络(数据源:http://vlado.fmf.unilj.si/pub/networks/data/)以及线虫神经网络[1]。这3个实际网络的盒维数在文献[13]中已计算得到。 Newman科学家合作网络具有1 589个节点与2 742条边,其中节点代表科学家,边代表两个科学家之间的合作关系。节点i和节点j之间权重值的计算方法为 (8) 美国航空网络具有306个节点和2 126条边,其中节点表示机场,边表示两个机场间存在航班。网络的权重值是指定期航班的客运量(单位:百万人次/年)。显然,当权重值越大时,表示两个机场关系密切,距离就越近(这里的距离并非指两个机场之间的地理距离),因此加权美国航空网络的权重类型也为相似权。根据式(5)求得网络中任意两个节点间的距离值后发现网络的直径为0.96。若采用传统的盒子长度赋值思想显然无法利用强度体积维数分析该网络的分形特性。因此必须采用新的盒子长度赋值思想,分析结果如图5b所示。通过拟合计算得到直线的斜率值为0.947,即加权美国航空网络的强度体积维数为0.947。 线虫神经网络具有306个节点和2 148条边,节点表示神经元,边表示神经元之间的连接,边的权重值由神经元之间的连接强度决定。当连接强度越大时权重值也越大,表明两个神经元间的关系越密切,距离就越近,因此加权线虫神经网络的权重类型仍然是相似权。利用强度体积维数分析加权线虫神经网络分形特性的结果如图5c所示。通过拟合计算得到直线的斜率值为1.088,即加权线虫神经网络的强度体积维数为1.088。 图5 强度体积维分析实际加权网络Fig.5 Fractal scaling analysis of real-world networks by the volume dimension method 从图5可以看出,当利用强度体积维数分析上述3个实际加权网络的分形特性时,这3个实际加权网络均在一定的尺度范围内表现出分形特性。强度体积维数的值均是在此尺度范围内通过对统计点进行线性拟合得到。更进一步地,采用文献[13]提出的BCANW算法分析上述3个加权网络的分形特性,并将分析结果与利用强度体积维数得到的结果进行对比。采用BCANW算法分析的结果如图6所示,对比结果如表3所示。 表3 强度体积维数与盒维数对比Tab.3 The results comparison between the volume dimensions and the box dimensions 从表3对两种维数的比较中可以看出,对于不同的实际网络,两个维数值的差异性表现差别很大。 其中美国航空网络的强度体积维数和盒维数差别最小,差值为0.128 1。其次为线虫神经网络,差值为0.303。最后为科学家合作网络,差值达到0.703。强度体积维数与盒子覆盖法的实质都是在给定的盒子长度下去覆盖网络节点,不同之处在于强度体积维是以一个节点为中心节点然后以r为半径覆盖,每次覆盖到的强度体积是一个确定的值,而在盒子覆盖法中寻找覆盖整个网络所需的最少盒子数量是一个NP完全问题,无法得到一个精确的值,这也是导致实际网络的强度体积维数值与盒维数值不一致的主要原因。 图6 BCANW算法分析实际加权网络Fig.6 Fractal scaling analysis of real-world networks by BCANW 在对实验数据(lnr,lnVS(r))线性拟合时,本文采用的方法是最小二乘拟合法,其实质是通过最小化误差的平方和来寻找数据点的最佳函数匹配。为了考察直线的拟合效果,这里考虑最小二乘拟合法的均方误差值Q,定义为 (9) 表4 强度体积维数和盒维数拟合结果对比Tab.4 The fitting results comparison between the volume dimensions and the box dimensions 从表4可以看出,对于科学家合作网络和美国航空网络,强度体积维数和盒维数计算过程中对应均方误差值都比较小,利用这两种维数均能发现其具有分形特性。对于线虫神经网络,强度体积维数计算过程中对应的均方误差值较小,为0.436 8,而盒维数计算过程中对应的均方误差值则达到0.735 0,接近于1,从图6c中也能发现其数据点较为分散,这说明加权线虫神经网络的分形特性用盒维数不易度量出。 本文以给定盒子长度下覆盖到的节点强度和来定义加权网络体积维数中“体积”的概念,提出了基于节点强度的加权网络体积维数概念。对两类构造的加权分形网络和3个实际加权网络的分析结果表明强度体积维数能够较好地度量加权网络的分形特性。此外,在对实际加权网络的分形分析中,同一网络的强度体积维数值与盒维数值并不一致。这主要是因为在盒子覆盖法中,寻找给定盒子长度下覆盖网络所需的最小盒子数量是一个NP完全问题,只能尽可能地找到最优解。而强度体积维在给定盒子长度下覆盖到的强度体积和是一个确定的值,有效地避免了NP完全问题。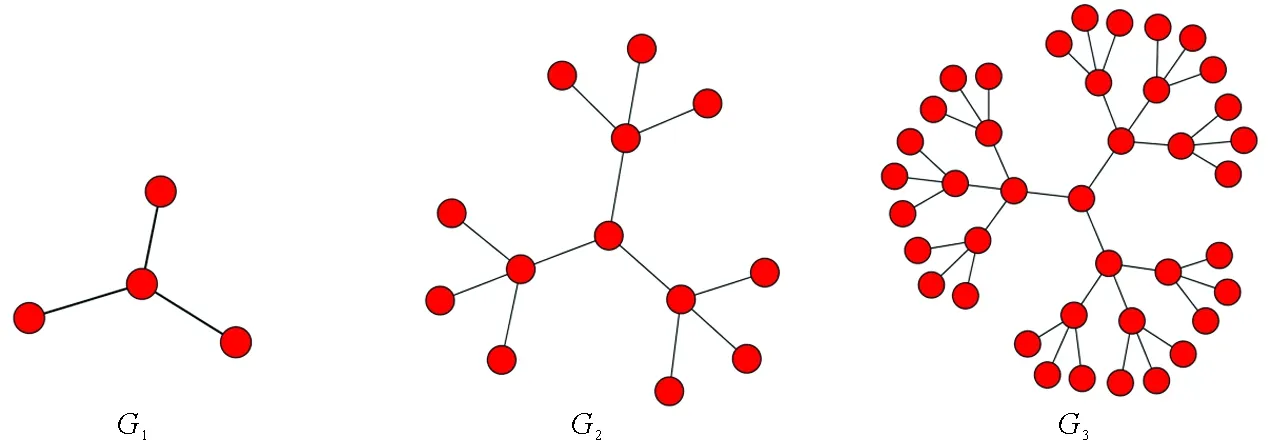


3.2 对实际网络的分析
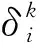

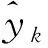

4 结论
