GABA算法的遥感图像分类
2018-02-28牛颖超周忠发王小宇
牛颖超,周忠发,王 历,王小宇
(1. 贵州师范大学喀斯特研究院,贵州 贵阳 550001; 2. 贵州省遥感中心,贵州 贵阳 550001; 3. 贵州省喀斯特山地生态环境国家重点实验室培育基地,贵州 贵阳 550001)
随着遥感技术的高速发展,遥感图像分类成为遥感应用领域中的热点与难点问题之一。为了提高遥感图像分类的精度和效率,许多学者对遥感图像分类算法进行了广泛深入的研究,常用的有监督分类、非监督分类和半监督分类[1-3]。但传统的分类方法已难以满足实际需求,因此本文提出了一种新颖的蝙蝠算法(GABA),运用于遥感图像分类。
蝙蝠算法是通过模拟蝙蝠的回声定位功能提出的一种智能优化算法。该算法通过改变蝙蝠的频率、响度、脉冲发射率,进行最优解的搜索,直到达到目标或满足条件停止操作。但蝙蝠算法具有后期收敛速度慢、寻优精度不高、易陷入局部最优值的缺点[4]。本文为了避免这个问题,将蝙蝠算法与遗传算法相结合创建一种新的遥感图像分类方法—GABA算法,将遗传算法中的选择、交叉、变异操作引入到蝙蝠算法中,增强种群多样性、全局搜索能力和寻优能力,从而弱化蝙蝠算法的缺陷,发挥两者之间的优势。通过试验与蝙蝠算法[5]、K-means算法[6-8]、粒子群算法[9-11]相比较,表明本文算法在遥感图像分类中具有较高的分类精度和分类效率。
1 蝙蝠算法

fi=fmin+(fmax-fmin)β
(1)
(2)
(3)
式中,β为一个随机向量,取值范围为[0,1];x*为比较n只蝙蝠所对应位置后当前全局最佳位置。λifi的改变会导致速度的增长,在求解不同的问题时,不改变λi(或fi)的同时改变fi(或λi)调整速度。在实际运用时,可以根据所感兴趣问题领域的大小,使用f∈(1,100),开始时每只蝙蝠随机分配频率,频率由[fmin,fmax]平均得出。
更新蝙蝠的位置之后,生成一个随机数,如果大于生成的随机数脉冲频率ri,就在随机游走中就近生成新的解决方案,即最佳解决方案。
xnew=xold+εAt
(4)

(5)
(6)
式中,α和γ都是恒量,α类似于模拟退火算法中冷却进程表中的冷却因素,对于任何0<α<1和γ>0的量都有
(7)
α和γ的值采用连续函数求优的参数值即:α=γ=0.9,控制蝙蝠速度和种群移动范围的主要参数为响度、脉冲发射率和频率,它们的取值范围分别为[1,0]、[1,0]和[2,0]。
最后判断蝙蝠的适应度函数的优劣,找出当前最优解,并迭代更新直到满足条件,输出最优解。
2 GABA算法
通过分析蝙蝠算法可以发现,该算法自身缺乏变异机制,若受到某个局部极值制约后很难挣脱,在进化过程中,种群的最优蝙蝠可能吸引其他个体迅速向自己聚集,导致种群多样性急剧下降,当许多蝙蝠个体越接近种群最优个体时,收敛速度下降甚至出现进化停滞的状况,致使种群丧失了进一步自身进化的能力,并且蝙蝠算法不能收敛到全局极值,这样就很难发现分布在局部最优邻域内的全局最优点。因此基于蝙蝠算法的遥感图像分类往往分类精度不高,容易出现错分现象。若想改进蝙蝠算法的遥感图像的分类精度,提高种群的多样性、全局搜索能力和寻优能力至关重要。本文针对蝙蝠算法的局限性,将遗传算法引入到蝙蝠算法中,对种群蝙蝠个体进行选择、变异、交叉操作,弥补蝙蝠算法的缺陷,发挥两者之间的优势,提高遥感图像的分类精度。
2.1 遗传算法
遗传算法是1975年由John Holland提出的,它是将每一个体进行编码,从一个初始化种群出发迭代更新,迭代的每一次都根据预定的目标适应度函数对种群的每个个体进行评价,利用适者生存的进化法则,模拟现实世界中的优胜劣汰进行选择、交叉、变异操作,不断得到更优的群体,并以全局并行搜索方式来搜索优化种群中的最优个体,求得满足要求的最优解[15-17]。
遗传算法的主要流程如下:
(1) 初始化:随机产生初始群体A(0)。
(2) 个体评价:计算群体A(n)中各个个体的适应度。
(3) 选择运算:将选择算子作用于群体。目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。
(4) 交叉运算:将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。
(5) 变异运算:将变异算子作用于群体。即是对群体中个体的某些基因上的基因值作变动。群体A(n)经过选择、交叉、变异运算之后得到下一代群体A(n+1)。
(6) 终止条件判断:如果满足终止条件,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
2.2 遗传算法与蝙蝠算法相结合(GABA算法)

(1) 初始化GABA算法的各个参数,设种群的大小为n,搜索空间维度为d,每个蝙蝠的位置和速度表示为s×r维变量,第i只蝙蝠的位置为xi,速度为vi,i=1,2,3,…,n。
(2) 计算种群个体的适应度函数,确定当前个体的最优解。若xi、bj满足
(8)
则xi为第j类,每个种群个体的适应度函数公式为
(9)
(3) 利用式(1)—式(3)更新蝙蝠的位置、速度和搜索脉冲频率。
(4) 更新蝙蝠的位置之后,生成一个随机数,如果大于生成的随机数脉冲频率,在随机游走中就近生成新的解决方案。
(5) 判断新的随机解决方案的数量是否Ai&f(xi) (6) 利用遗传算法以每一个蝙蝠位置为初始点进行选择、交叉、变异操作,得到新的蝙蝠位置和速度,公式如下 if(Ri (10) 式中,Ri(i∈M)为均匀分布在[0,1]的随机变量,M为适应度较差的部分粒子;R2为介于[0,1]的随机变量;R3为随机变量,当随机数小于0.5时为1,大于0.5时为-1,以此来更新这部分蝙蝠的位置和速度。 (7) 根据蝙蝠种群个体的适应度函数的优劣,更新最优解。 (8) 迭代更新判断是否为最优解,否则转到第(3)步继续运行。 本文试验数据选取江苏省常州市某地区高分二号遥感图像作为试验数据,试验区主要包括水体、建筑用地、裸地、道路、水田、旱地、林地、草地等地物,进行图像分类前,首先对图像进行预处理。本文采用双线性内插法对图像进行几何校正,并利用短波红外波段,从图像中选取亮度值较低的水体为参照,对图像进行相对辐射校正,然后进行重采样处理。处理后影像如图1所示。 图1 研究区遥感影像图 本试验操作系统为Windows 7,编译软件为Matlab 2015A,硬件为Intel(R) Core(TM) i5-4460 CPU@ 3.20 GHz。遥感图像的分类数目为8类,最大迭代次数为100,b1、b2代表加速常数,本试验b1为2.8,b2为1.3,Bv取0.8,Bm取1。然后运用GABA算法进行分类,如图2所示。 图2 GABA算法的分类结果 精度验证是遥感分类过程中不可缺少的一部分,通过精度分析可以有效地获取分类结果中的信息。常用的精度验证有误差矩阵方法、统计比较法[18]。其中误差矩阵是评价分类识别精度的基本参数,它是将遥感影像分类后的结果与相应的地物真实分布图或更高分辨率的影像进行对比,得出各类地物的分类误差[19-21]。误差矩阵一般分为3种精度指标:总体精度(overall accuracy)、制图精度(producers accuracy)、用户精度(users accuracy),本文采用混淆矩阵对研究区的分类结果进行精度评价[22]。 (1) 总体精度是误差矩阵中分类的正确像元总数与所有像元总数的比值,即每一个随机样本的分类结果与真实类型相一致的概率。 (2) 制图精度是用某一种类别正确的像元除以该类总检测像元个数,即参考像元被正确分类的概率。 (3) 用户精度是采用一个类别的正确像元总数除以实际上被分到该类像元的总数,即图上分到该类的像元在地面上实际代表该类的概率。 上述统计量可以用来评价图像分类的单个类别的分类精度。但利用总体精度、制图精度或用户精度的弊端是像元类别的变化可能导致自身的百分比随之变化,但Kappa系数考虑了误差矩阵中所有的因子,能够全面反映总体分类精度[23-24]。计算公式为 (11) 式中,k为误差矩阵的总列数,即样本的总类别;xii为误差矩阵中第i行、第i列的值;xih、xih分别为第i行、第i列的总像元数;N为地表真实分类中的总像元数。 本文选取9867个点基作为检验数据,将GABA算法的分类结果建立混淆矩阵进行精度评价见表1。从表1中可以看出本文算法的总体精度为95.62%,Kappa系数为0.948 4,分类精度高、结果较优。从单个地物的分类精度来看,在研究区中水体的用户精度为90.25%,虽然比其他地物的用户精度较低,但良好地区分出与水体光谱特征相似的建筑用地阴影及阴面的林地。建筑用地和道路的光谱信息类似,运用本文算法,建筑用地与道路的用户精度分别为92.27%、90.21%,使两者得到了较好的识别。通常裸地分类时容易与建筑用地、道路混淆,而裸地的用户精度为97.80%,分类效果较为满意。水田分类时容易受水体干扰,其用户精度为96.92%,信息较精确地被提出。旱地的用户精度最高为99.89%,表明本文算法在识别旱地时具有一定的优势。一般情况下林地和草地两者不易区分,而表1中它们的用户精度分别为92.60%、91.62%,得到了良好的区分。 表1 GABA算法的精度评价结果 本文分别运用蝙蝠算法、K-means算法、粒子群算法与GABA算法进行对比分析,以此突出GABA算法的优越性,蝙蝠算法、K-means算法、粒子群算法的分类结果如图3所示,分类精度见表2。 从分类效果来看,本文算法的总体精度为95.62%,Kappa系数为0.098 1,分类效果最优,这是由于引入变异机制之后,算法具有更强的全局搜索能力,到迭代后期,使得种群中个体的差异变小,同时也具有更强的局部搜索能力,能准确地提取出目标地物,致使不同地物类型之间得到较好的区分;蝙蝠算法由于自身存在缺陷,导致近似光谱信息的地物容易受到相互干扰,总体精度和Kappa系数最低,分类效果最差;K-means算法的总体精度与Kappa系数分别为83.96%、0.801 4,分类精度相对较低,分类结果中存在一些错误分类;粒子群算法的分类精度不高,但比K-means算法的分类效果好,总体精度为89.73%,Kappa系数为0.876 3,能够区分面积比较大的分类区域。从分类时间来看,本文算法所需的运行时间最短,K-means算法的运行时间最长,粒子群算法的运行时间介于蝙蝠算法和本文算法之间,而蝙蝠算法虽然比粒子群算法效率高但比本文算法效率低。因此本文算法分类时间短,具有较高的效率。 图3 不同算法的分类结果 方法蝙蝠算法K⁃means算法粒子群算法本文算法总体精度/(%)78.5583.9689.7395.62Kappa系数0.75370.80140.87630.9484运行时间/s0.11720.21350.19480.0981 本文提出了一种GABA算法的遥感图像分类方法,该方法针对蝙蝠算法后期收敛速度慢、寻优精度不高、易陷入局部最优值的缺点,将遗传算法融入蝙蝠算法中,对种群蝙蝠个体进行选择、变异、交叉操作,从而增强蝙蝠种群多样性、全局搜索能力和寻优能力,弱化蝙蝠算法的缺陷,发挥两者之间的优势,提高遥感图像分类精度与效率。为验证该方法有效,试验选取蝙蝠算法、K-means算法、粒子群算法与本文算法进行比较,分析评价遥感图像的分类结果,试验表明本文算法在遥感图像分类应用中提高分类精度的同时也减少了分类时间,是一种有效的分类方法,在遥感图像分类中具有广泛的应用前景。 [1] HUANG X, ZHANG L. An SVM Ensemble Approach Com-bining Spectral, Structural, and Semantic Features for the Classification of High-Resolution Remotely Sensed Imagery[J]. Geoscience & Remote Sensing IEEE Transactions on, 2013, 51(1):257-272. [2] 樊利恒,吕俊伟,邓江生.基于分类器集成的高光谱遥感图像分类方法[J].光学学报,2014, 34(9):91-101. [3] 郭玉宝, 池天河, 彭玲,等. 利用随机森林的高分一号遥感数据进行城市用地分类[J]. 测绘通报, 2016(5):73-76. [4] 李枝勇,马良,张惠珍.蝙蝠算法收敛性分析[J].数学的实践与认识,2013, 43(12):182-190. [5] 陈海挺.改进蝙蝠算法优化极限学习机的图像分类[J].激光杂志,2014(11):26-29. [6] BANDYOPADHYAY S, MAULIK U. An Evolutionary Technique Based on K-means Algorithm for Optimal Clustering in RN [J]. Information Sciences, 2002, 146(1-4):221-237. [7] TANG R, FONG S, YANG X S, et al. Integrating Nature-inspired Optimization Algorithms to K-means Clustering[C]∥Seventh International Conference on Digital Information Management. [S.l.]: IEEE, 2012:116-123. [8] 陈华,陈书海,张平,等.K-means算法在遥感分类中的应用[J].红外与激光工程,2000, 29(2):26-30. [9] 丁胜,袁修孝,陈黎.粒子群优化算法用于高光谱遥感影像分类的自动波段选择[J].测绘学报, 2010, 39(3):257-263. [10] 蒋韬.基于遗传粒子群优化算法的遥感图像分类方法研究与应用[D].北京:首都师范大学,2013. [11] 付建东.粒子群神经网络在遥感影像分类中的应用研究[D].南昌:东华理工大学,2015. [12] YANG X S. A New Metaheuristic Bat-Inspired Algorithm[J]. Computer Knowledge & Technology, 2010, 284:65-74. [13] YANG X S, HE X. Bat Algorithm: Literature Review and Applications[J]. International Journal of Bio-Inspired Computation, 2013, 5(3):141-149. [14] YANG X, GANDOMI A H. Bat Algorithm: a Novel Approach for Global Engineering Optimization[J]. Engineering Computations, 2012, 29(5):464-483. [15] 张铃,张拔.遗传算法机理的研究[J]. 软件学报,2000,11(7):945-952. [16] 臧淑英,张策,张丽娟,等.遗传算法优化的支持向量机湿地遥感分类——以洪河国家级自然保护区为例[J].地理科学,2012, 32(4):434-441. [17] 黄明,吴延斌.基于混沌遗传算法的遥感影像分类[J].测绘科学,2011, 36(2):5-8. [18] 王卫红,严鲁琴,金丹丹,等.基于GEPSO模型的面向对象遥感图像分类[J].计算机科学,2015, 42(5):51-53. [19] CLEVE C, KELLY M, KEARNS F R, et al. Classification of the Wildland-urban Interface: A Comparison of Pixel and Object-based Classifications Using High-resolution Aerial Photography [J]. Computers Environment & Urban Systems, 2008, 32(4):317-326. [20] 刘大伟,韩玲,韩晓勇.基于深度学习的高分辨率遥感影像分类研究[J].光学学报, 2016(4):298-306. [21] 吴洋.基于超像素的面向对象遥感图像分类方法研究[D].武汉:华中科技大学,2013. [22] 明冬萍, 邱玉芳, 周文. 遥感模式分类中的空间统计学应用——以面向对象的遥感影像农田提取为例[J]. 测绘学报, 2016, 45(7):825-833. [23] 彭海涛,柯长青.基于多层分割的面向对象遥感影像分类方法研究[J].遥感技术与应用,2010, 25(1):149-154. [24] 葛春青,张凌寒,杨杰.基于决策树规则的面向对象遥感影像分类[J].遥感信息,2009(2):86-90.3 试验与分析
3.1 试验数据

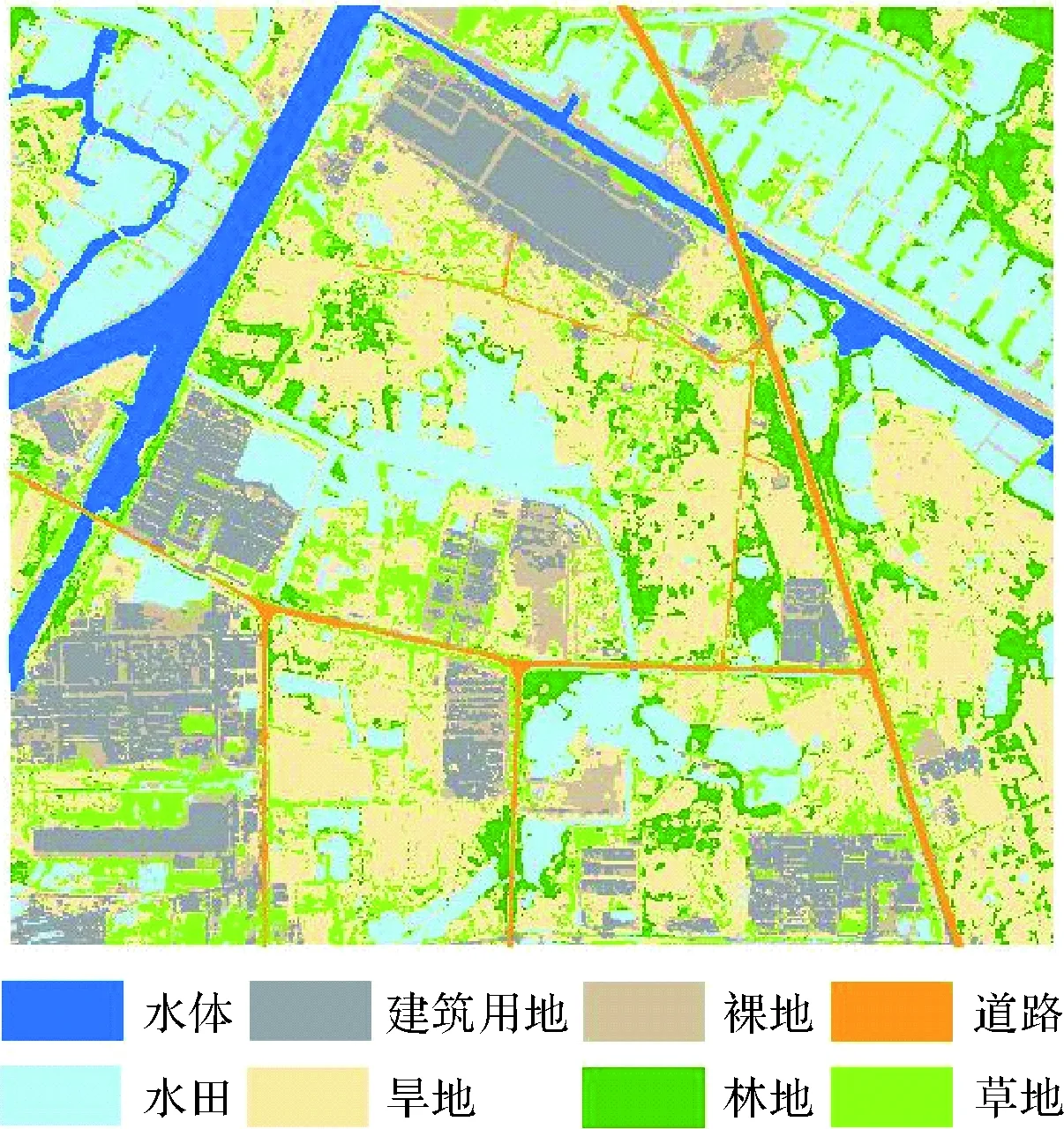
3.2 精度验证与分析
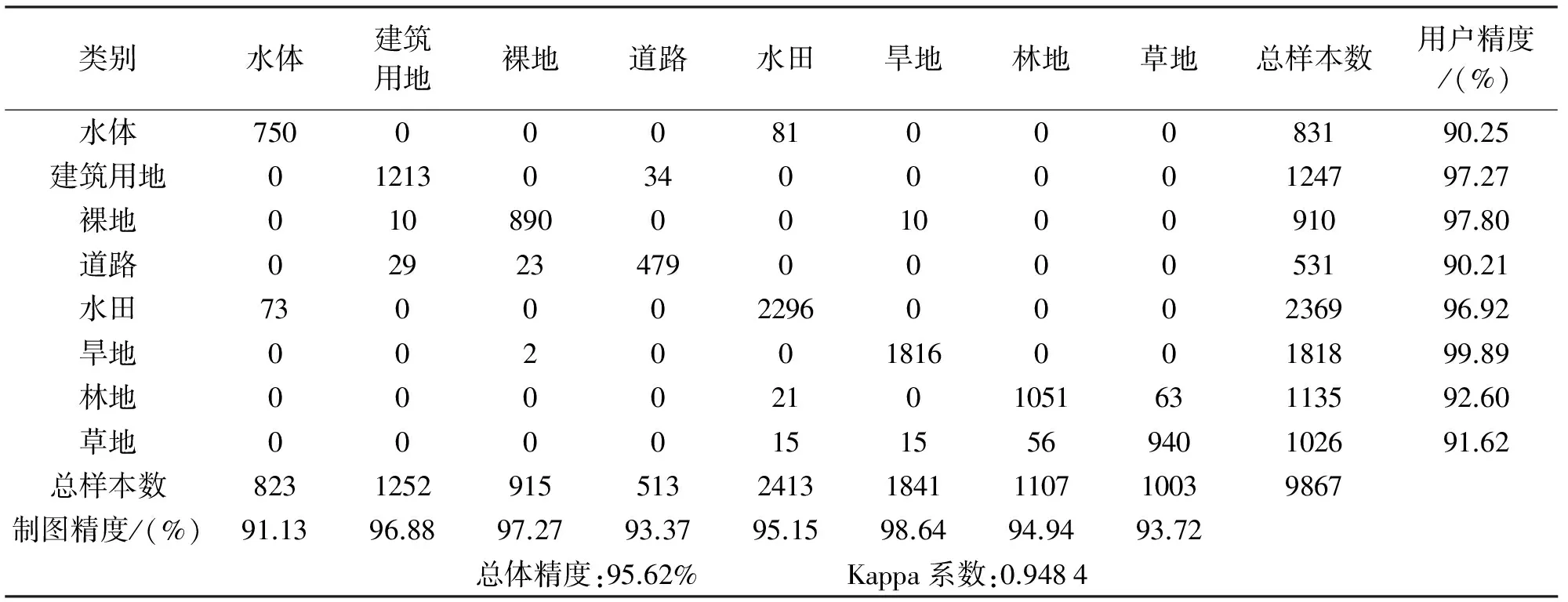
3.3 与其他分类算法对比分析

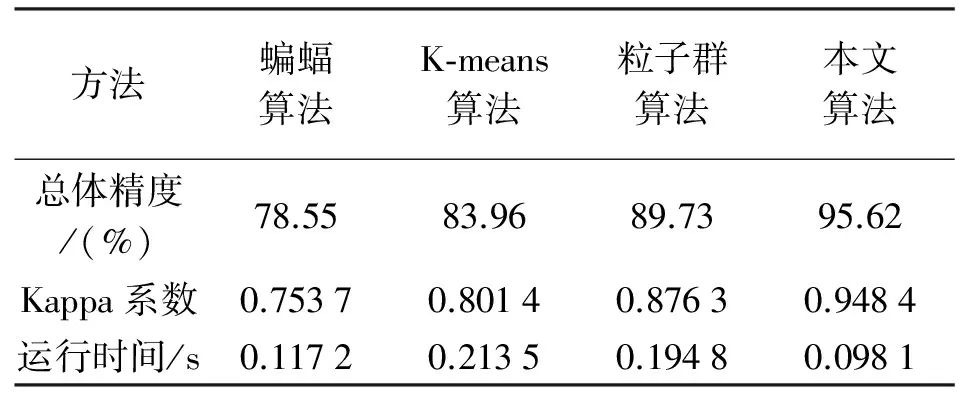
4 结 语
