BDS/GPS实时钟差估计中ISB分析与函数模型设计

谷守周，施 闯，党亚民，秘金钟，薛树强，张龙平,3

(1. 武汉大学卫星导航定位技术研究中心，湖北 武汉 430079； 2. 中国测绘科学研究院，北京 100830； 3. 山东科技大学,山东 青岛 266590)

北斗卫星导航系统(BeiDou Satellite Navigation System，BDS)是我国自主研发、独立运行的全球卫星导航系统[1-4]。自2012年底向亚太大部分地区提供正式运行服务以来，BDS系统已广泛应用于交通运输、海洋渔业、水文监测、大地测量、车载导航等领域。随着实时高精度定位用户的逐渐增加，如何满足对BDS实时高精度服务不断增长的需求是当前研究的热点。

精密轨道与钟差是卫星导航定位系统实现高精度定位的前提条件，目前IGS分析中心和我国的iGMAS(International GNSS Monitoring & Assessment System)产品综合中心提供多模GNSS(BDS/GPS/GLONASS/Galileo)精密轨道和钟差产品，并应用于事后的精密定位[5-6]。事后产品不能满足用户的实时性需求，因此需开展实时轨道和实时钟差的估计策略研究。卫星精密轨道具有可预报性，实时轨道可利用计算的精密轨道进行预报得到，应用于实时定位。由于导航卫星原子钟易受外界及本身因素的影响，变化极为复杂，很难利用数学模型进行预报，必须进行实时估计[7-12]。

在GNSS组合定位与定轨中，由于时空基准、信号体制等因素的差异导致卫星信号在接收机内部会产生相应的不同的硬件延迟，称为系统间偏差(inter-system bias，ISB)[13-14]。在常规的GNSS组合定位时，如BDS/GPS组合，需选定GPS作为基准系统，对每个接收机增加一个BDS相对于GPS的系统间偏差进行估计[12，15]。但相比于GPS，BDS系统由GEO(geosynchronous orbit)、IGSO(inclined geosynchronous satellite orbit)和MEO(medium earth orbit)3种轨道类型的卫星组成，各星座的系统偏差的是否一致性尚待进一步分析。

针对北斗GEO/IGSO/MEO的星座差异，本文介绍了基于非差观测量的实时钟差估计方法，研究分析了不同测站接收机的BDS GEO/IGSO/MEO ISB的差异，提出了在实时钟差估计函数模型中引入3个ISB参数，以解决由BDS星座构型差异引发的系统偏差问题，利用根据该方法实现的软件，基于MGEX数据和湖南CORS站实时观测数据，生成BDS/GPS组合的实时钟差产品，并与原有方法生成的钟差产品对比分析，验证了算法的有效性。

1 基于非差观测值的实时钟差估计方法

1.1 GNSS观测方程

在基于双频观测数据的BDS/GPS组合的实时钟差估计中，一般采用消去电离层一阶项的非差消电离层组合观测值进行计算[13]，引入一个BDS ISB偏差，其观测方程可表示为

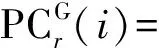
(1)

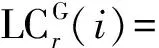
(2)

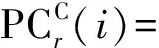
(3)

(4)

式中，r和i分别表示测站和历元编号；G和C分别表示GPS和BDS卫星；PC、LC分别表示伪距和载波相位的无电离层组合观测值；P1、P2、L1、L2分别表示两个频率上的伪距和载波相位观测值；f1、f2分别表示两个频率的波长；c为光速；δtr为接收机钟差；δts为卫星钟差；M表示测站与卫星间的对流层投影函数；ZTD为测站的天顶对流层延迟值；NLC为无电离层线性组合模糊度，为非整数；λLC为无电离层组合波长；cδtC_G表示BDS相对于GPS的ISB；εPC和εLC分别表示伪距和载波相位的多路径、观测噪声等未模型化的其他误差。

针对BDS GEO/IGSO/MEO ISB参数不一致的问题，本文从函数模型出发，提出一种基于“三参数”的BDS/GPS实时钟差估计算法，即在BDS/GPS组合进行实时钟差解算时，分别对BDS GEO、IGSO和MEO引入一个ISB参数，即将cδtC_G进行以下拓展

δtC_G=a(1)·δtGEO+a(2)·δtIGSO+a(3)·δtMEO

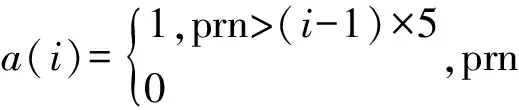
如果以式(1)—式(4)为观测方程求解卫星钟差参数，法方程是奇异的。为了能够求解钟差参数，必须引入一个基准钟，求解其他接收机钟差和卫星钟钟差相对于该基准钟的钟差。相关文献已经证明，只要保证基准钟的钟差精度优于10-6s，相对钟差和绝对钟差对用户定位结果是等价的，即相对钟差的系统性偏差在用户定位模型中可完全被用户接收机钟差吸收，不影响用户的定位精度[14]。

1.2 实时钟差估计方法

均方根滤波是一种改进的卡尔曼滤波算法，该算法简单、数据稳定性高，特别适用于进行实时数据处理[16]。本文非差实时钟差估计方法采用均方根滤波方法。

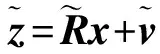
(5)

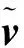
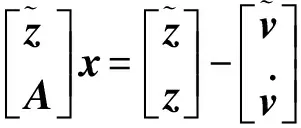
(6)

两侧乘以正交变换矩阵T可得

(7)

可由Householder变换得到

(8)

2 不同星座系统间偏差分析

为分析BDS不同星座的卫星导致的系统间偏差的一致性，本文选取了由4家接收机厂商生产的24个具备BDS接收能力的MGEX观测站接收机，对BDS GEO/IGSO/MEO相对于GPS的ISB进行分析。部分测站的接收机类型见表1。

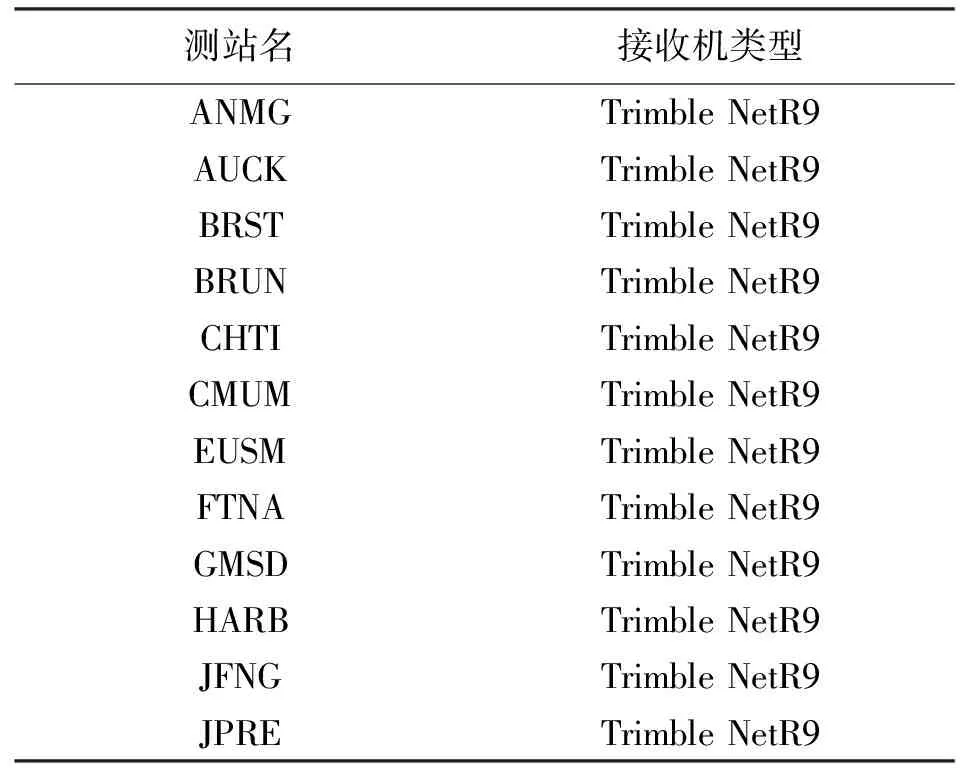
表1 部分MGEX测站接收机类型

基于2016年11月22—28日(年积日327—333)包含24个已选测站在内的110个IGS/MGEX观测站观测数据(采样率为30 s)，利用中国测绘科学研究院iGMAS分析中心定轨软件，将BDS GEO/IGSO/MEO卫星分别与GPS进行联合定轨，经统计得到BDS GEO/IGSO/MEO相对于GPS系统的ISB信息，如图1—图3所示。

从图1—图3可知，从单接收机来看，各测站多天的GEO/IGSO/MEO的ISB变化趋势一致，但参数值差异较大，其中GEO与IGSO/MEO的差异显著。从不同类型的接收机来看，同一厂商的接收机GEO/IGSO/MEO的ISB具有较为一致的变化趋势，如18台Trimble NetR9的3种不同星座卫星的ISB值都在20 ns以内，Leica GR10接收机的ISB 40 ns左右，Leica GR25接收机的ISB在20 ns，JAVAD TRE_G3TH DELTA接收机的ISB在40 ns。

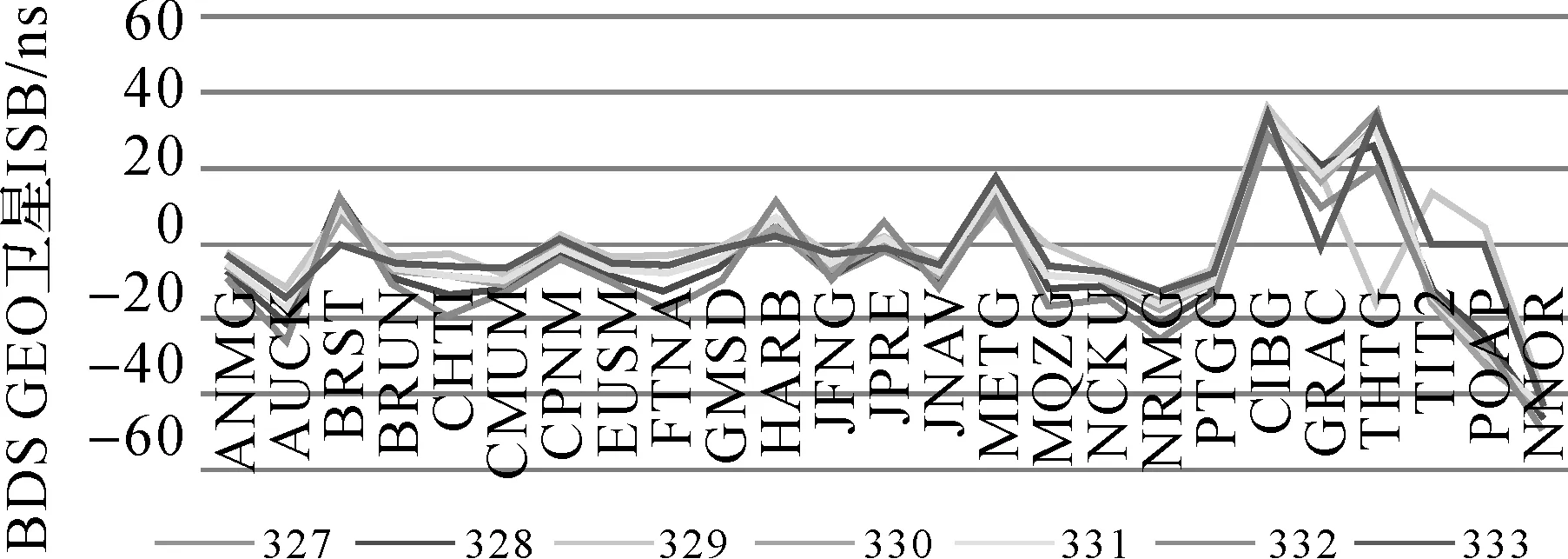
图1 BDS GEO卫星相对于GPS的系统间偏差

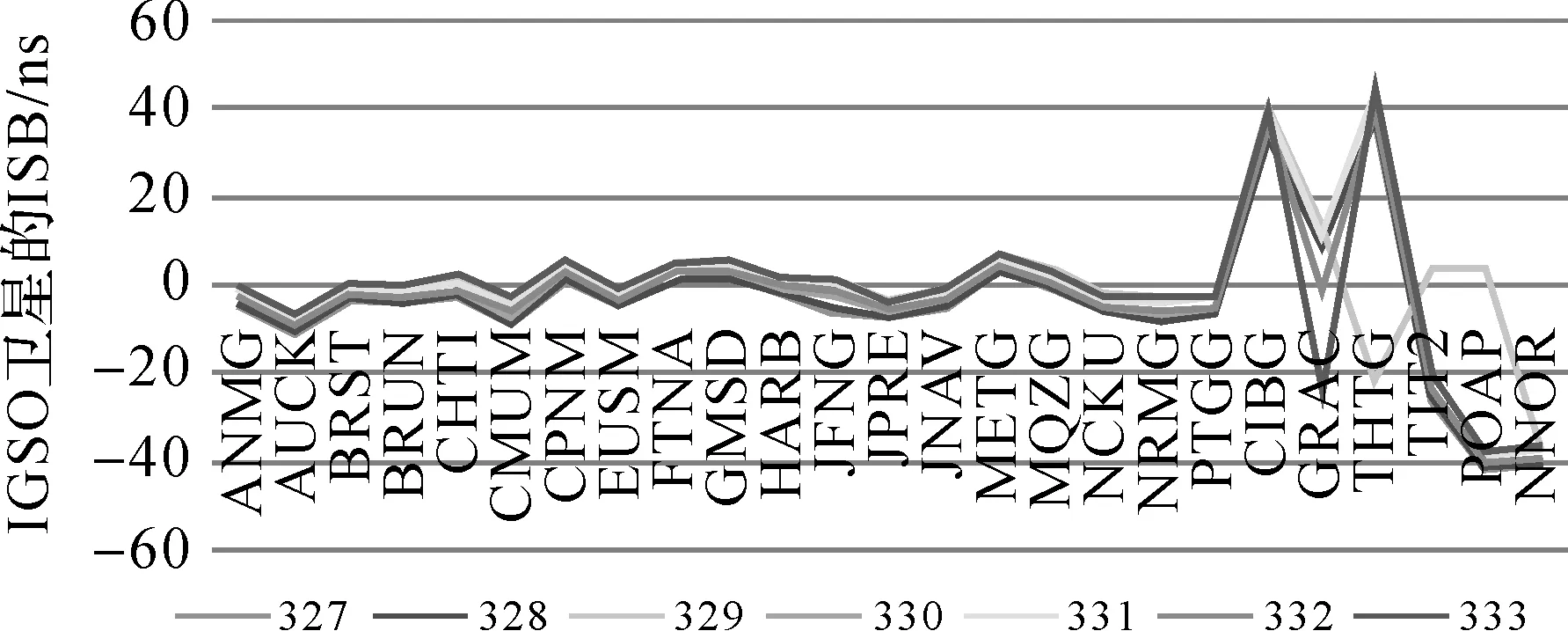
图2 BDS IGSO卫星相对于GPS的系统间偏差

图3 BDS MEO卫星相对于GPS的系统间偏差

为进一步分析各星座和各类型接收机的ISB差异，本文从最大值、最小值和均值3个方面进行了统计分析，结果见表2。

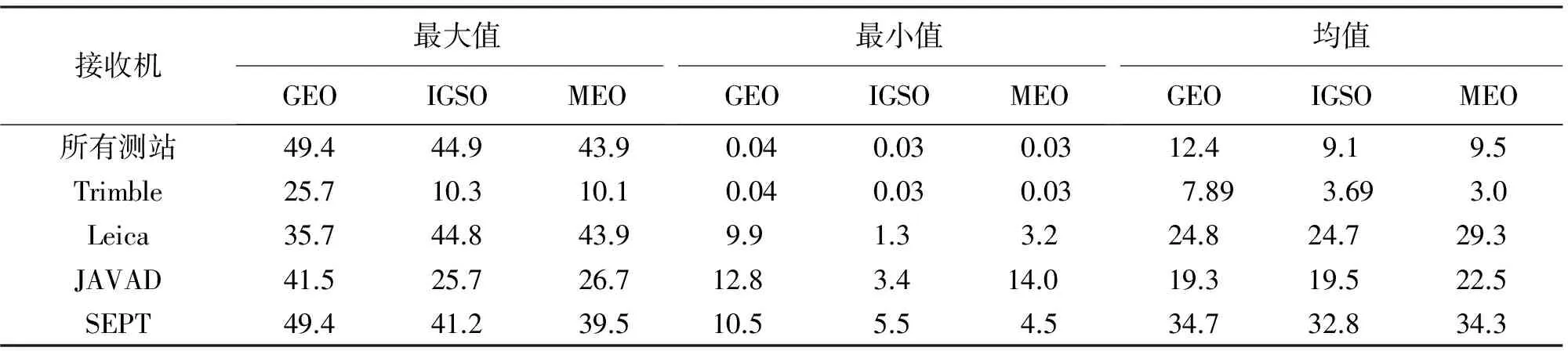
表2 BDS卫星ISB统计 ns

由表2可知，从最大值来看，GEO卫星与IGSO/MEO的ISB存在较大差异，可达十几纳秒，IGSO/MEO之间差异相对较小，约10 ns；从最小值来看，GEO/IGSO/MEO的ISB差异与接收机密切相关，Trimble接收机3个不同卫星星座ISB相当，Leica/SEPT接收机表现为GEO卫星与IGSO/MEO的ISB存在较大差异，可达10 ns，IGSO/MEO的ISB差异在纳秒级；JAVAD接收机表现为GEO/MEO与IGSO之间存在较大差异，约10 ns。从均值来看，GEO/IGSO/MEO的ISB差异与接收机密切相关，Trimble接收机表现为GEO卫星与IGSO/MEO的ISB存在较大差异，可达4 ns，IGSO/MEO小于1 ns，Leica/JAVAD接收机表现为MEO卫星与GEO/IGSO的ISB存在较大差异，可达4 ns，IGSO/MEO小于1 ns，SEPT接收机表现为GEO/MEO与IGSO之间存在较大差异，约2 ns。

总的来看，BDS GEO/IGSO/MEO不同星座之间存在较大差异，其差异与接收机密切相关，最大可达几十纳秒，在进行北斗实时钟差解算时需顾及BDS卫星不同星座差异，将有利于改善BDS卫星的钟差精度。

3 数据试验与结果分析

3.1 试验数据与解算策略

本文在中国测绘科学研究院现有的实时钟差解算软件的基础上，对上述算法进行了软件实现，具体思想是在选取多GNSS组合实时钟差解算时对BDS系统引入3个ISB参数，即使在单BDS系统实时钟差解算时，仍需增加引入2个ISB参数。

为验证上述分析的实时钟差的解算性能，本文选取了2016年12月1日全球78个MGEX站和2个湖南省CORS站的实时观测数据(数据采样率1 s)，分别采用1个ISB参数和本文提出的3个ISB参数两种方法开展了BDS/GPS组合的实时钟差解算，对生成的钟差产品进行统计分析。

本文用于实时钟差估计的观测值先验信息、各项误差改正模型及参数处理策略见表3。

3.2 实时钟差评估方法

实时钟差精度评估选取iGMAS事后精密钟差产品作为参考，由于两套钟差产品所选的基准钟不同，会导致钟差值之间存在一定的系统性偏差，但是这种系统性偏差在定位中被模糊度和接收机钟差吸收，不影响最终定位结果。因此，在分析实时钟差产品与事后精密产品的符合程度时，需首先将两套钟差产品的基准钟统一，消除系统偏差影响，具体方法为采用二次差方法消除基准偏差后进行钟差精度评定，即

(9)

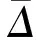
表3 卫星钟差实时估计策略

3.3 结果分析

利用中国测绘科学研究院iGMAS分析中心的钟差精度分析软件，统计分析了两种策略下BDS/GPS实时钟差精度。

3.3.1 不同策略下GPS实时钟差精度分析

利用iGMAS事后精密钟差文件，选取GPS PRN01卫星作为基准，对两种计算策略下的实时钟差产品进行精度统计，统计结果如图4—图5所示。

从图4可知，在进行实时钟差估计时，引入1个ISB参数和3个ISB参数对GPS实时钟差的精度相当，两种策略的GPS实时钟差精度都优于0.2 ns；从图5可知，两种策略下的精度差异都基本都在10 ps左右，最大值小于20 ps。基于各卫星精度统计结果，求取两种策略下31颗卫星的精度均值分别为78.7和80 ps，精度降低了1.63%，因此,在进行BDS/GPS组合实时钟差解算时引入1个和3个ISB参数对GPS实时钟差精度影响可忽略。

3.3.2 不同策略下BDS实时钟差精度分析

利用iGMAS事后精密钟差文件，选取BDS PRN09卫星作为基准，对两种计算策略下的实时钟差产品进行精度统计，统计结果如图6—图7所示。

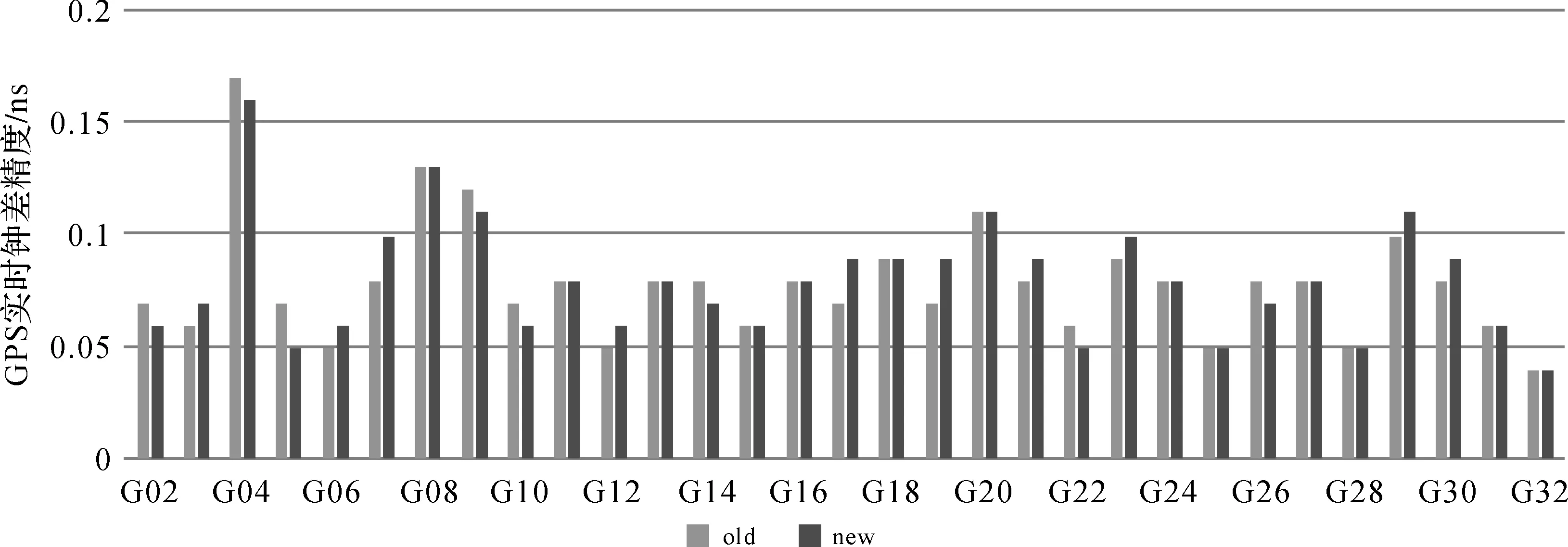
图4 GPS实时钟差精度对比(old：1个ISB参数，new：3个ISB参数)

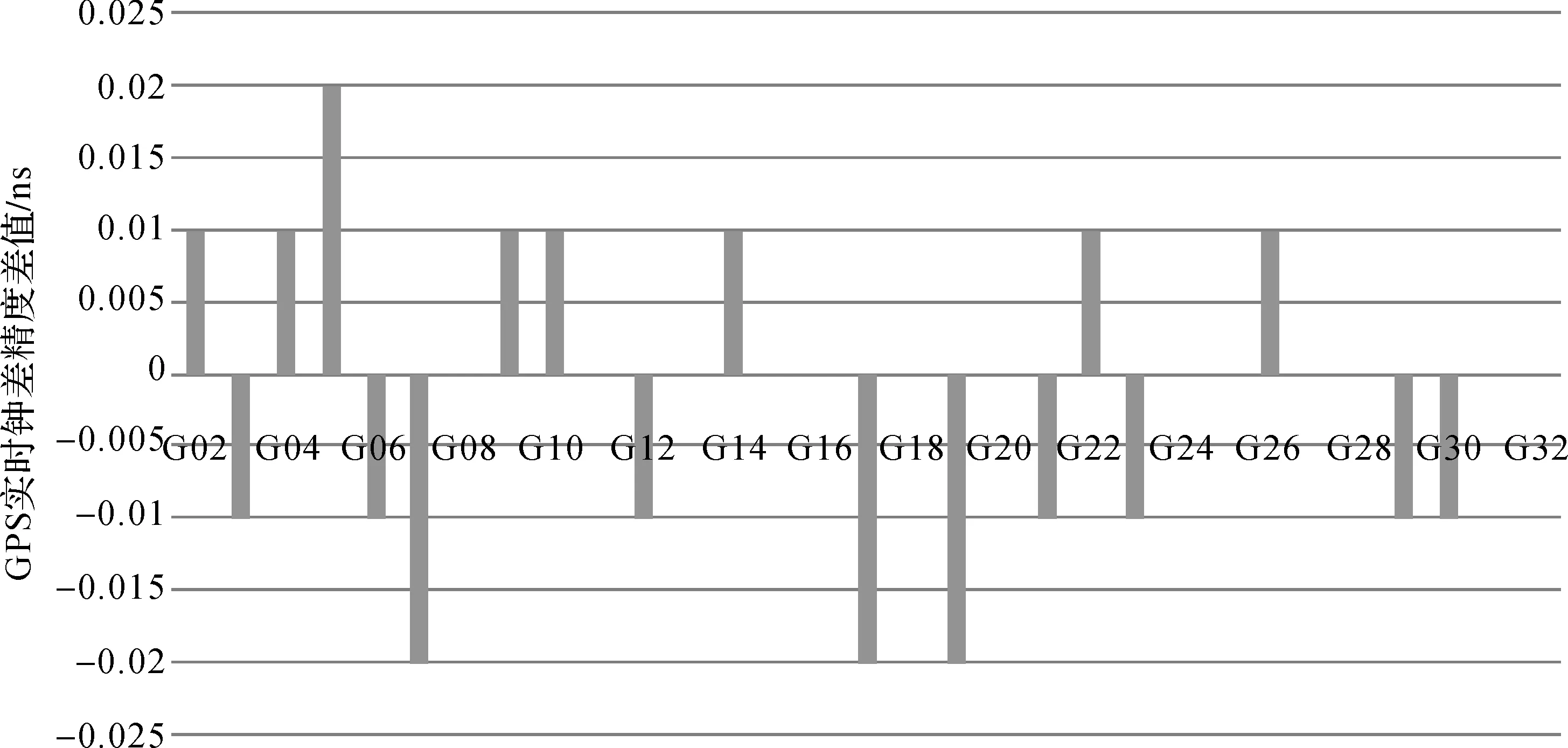
图5 两种策略下的GPS精度差值

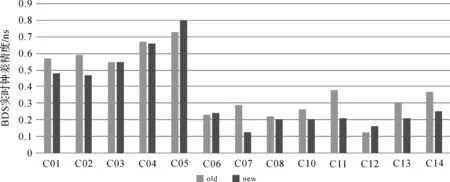
图6 BDS实时钟差精度对比(old：1个ISB参数，new：3个ISB参数)

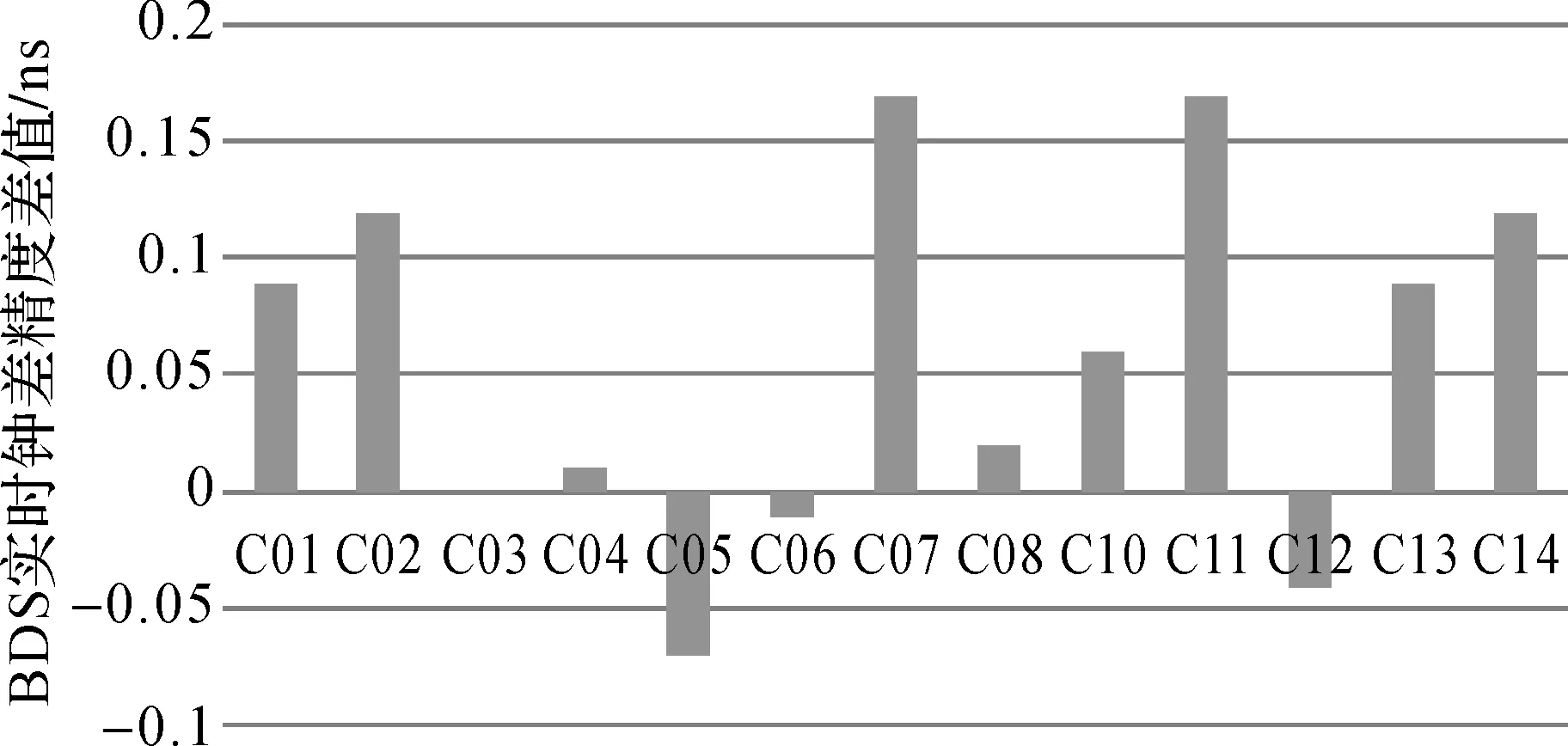
图7 两种策略下的GPS精度差值

从图6、图7可知， 针对GEO卫星而言，C01、C02的卫星钟差精度分别提高了0.09和0.12 ns，C03和C04精度略有提高，C05精度降低了0.07 ns，对GEO卫星星座整体统计，其精度均值分别为0.62和0.59 ns，精度提高比例为4.8%；针对IGSO卫星而言，C07、C08、C10的卫星钟差精度分别提高了0.17、0.02和0.06 ns，C05精度降低了0.01 ns，对IGSO卫星星座整体统计，其精度均值分别为0.25和0.19 ns，精度提高比例为24%；针对MEO卫星而言，C11、C13、C14的卫星钟差精度分别提高了0.17、0.09和0.12 ns，C05精度降低了0.04 ns，对MEO卫星星座整体统计，其精度均值分别为0.29和0.21 ns，精度提高比例为29%。两种处理策略下的BDS GEO/IGSO/MEO实时钟差精度有明显提高，从整体均值来看，两种策略下的均值分别为0.406和0.35 ns，精度提高13.8%。

通过分析可知，在进行BDS/GPS组合实时钟差解算时，引入3个ISB参数可在基本不损失GPS实时钟差精度的前提下提高BDS实时钟差的精度，特别是对BDS IGSO和MEO，提高比例可达20%以上，对GEO卫星实时钟差有所提高，但效果不显著。

4 结 论

本文通过分析不同接收机BDS GEO/IGSO/MEO的差异，提出了顾及BDS星座差异的BDS/GPS组合实时钟差估计的函数模型，利用实际数据计算分析，得到如下结论：

(1) 通过在函数模型中引入3个参数，消除了BDS GEO/IGSO/MEO 3种不同类型轨道卫星星座的系统差异，优化了BDS/GPS组合的函数模型。

(2) 同一厂商的接收机BDS GEO/IGSO/MEO的ISB偏差基本在同一量级，变化趋势相似；不同厂商的接收机BDS GEO/IGSO/MEO的ISB偏差较大，可达几十纳秒。

(3) 引入“三参数”函数模型得到的GPS实时钟差产品精度与原有模型相当。

(4) 引入“三参数”函数模型可改进BDS实时钟差的精度，其中IGSO/MEO改进显著，提高幅度在20%以上，对GEO卫星的精度略有改善，约4%。

[1] 杨元喜，陆明泉，韩春好. GNSS互操作若干问题[J]. 测绘学报，2016，45(3)：253-259.

[2] 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报，2010，39(1)：1-6.

[3] 杨元喜. 北斗卫星导航系统与测绘学科发展[J]. 测绘科学技术学报，2015，32(1):2.

[4] 刘瑞华,赵庆田,吕小平，等.“北斗区域导航系统”非精密进近导航性能分析[J].中国空间科学技术,2015,35(4):53-59,83.

[5] 罗璠，李建文，黄海，等.BDS广播星历的轨道误差分析[J].测绘通报，2015(2)：70-72.

[6] ZUMBERGE J F，HEFLIN M B，JEFFERSON D C,et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal Geophysical Research Solid Earth,1997,102(B3):5005-5017.

[7] LOU Y，LIU Y，SHI C，et al.Precise Orbit Determination of BeiDou Constellation Based on BETS and MGEX Network[J]. Scientific Reports,2014,4(8):1255-1264.

[8] 赵齐乐，戴志强，王广兴，等.利用非差观测量估计北斗卫星实时精密钟差[J].武汉大学学报(信息科学版)，2016，41(5)：686-691.

[9] GE M，CHEN J，DOUA J，et al.A Computationally Efficient Approach for Estimating High-rate Satellite Clock Corrections in Realtime[J].GPS Solutions,2012,16(1):9-17.

[10] HUANG G，ZHANG Q，XU G.Real-time Clock Offset Prediction with an Improved Model[J]. GPS Solutions，2014，18(1):95-104.

[11] 蔡华，赵齐乐，楼益栋. 精密卫星钟差确定系统的实现与精度分析[J]. 武汉大学学报(信息科学版)，2009，34(11):1293-1296.

[12] 徐龙威,刘晖,刘玉洁，等.一种顾及GNSS系统间偏差的伪距单点定位方法[J].大地测量与地球动力学,2016,36(9):813-816.

[13] 陈良，耿长江，周泉.北斗/GPS实时精密卫星钟差融合解算模型及精度分析[J]. 测绘学报，2016，45(9)：1028-1034.

[14] 叶世榕.GPS非差相位精密单点定位理论与实现[D].武汉:武汉大学，2002.

[15] 刘志强，王解先，段兵兵.单站多参数GLONASS码频间偏差估计及其对组合精密单点定位的影响[J]. 测绘学报，2015，44(2)：150-159.

[16] BIERMAN G J. Factorization Methods for Discrete Sequential Estimation[M].New York:Academic Press,1977.