大规模电网运行方式调整潮流计算及病态诊断

彭慧敏, 李 峰, 袁虎玲, 鲍颜红

(南瑞集团(国网电力科学研究院)有限公司, 江苏省南京市 211106)

0 引言

特高压跨区大容量交直流混联电网具有很大的输电优势,同时也给大规模电网潮流计算分析带来了挑战。采用目前已有算法对大规模的交直流混联网络进行潮流计算时,容易碰到潮流不收敛的问题,因此提高潮流算法的收敛性能显得尤为迫切。

牛顿—拉夫逊(NR)法[1]是计算潮流分布的传统方法,其基本思路是把非线性方程组局部线性化,根据不平衡量求解线性化后的方程,逐步寻找潮流解。为解决牛顿潮流法的初值敏感问题,通常先采用PQ分解法[2]或高斯—赛德尔(G-S)法[3]迭代1至2次,获取合适的给定初值,再进行NR迭代。为提高大规模电力系统潮流计算收敛性,典型的方法主要有最优乘子法[4]、张量法[5-6]、自适应列文伯格—马夸尔特(LM)方法[7-8]。

目前,国内外大型的商业电力系统分析软件大都先采用PQ分解法在给定的PQ迭代次数内获取最佳初值,再在NR设定的迭代次数内迭代获取满足收敛精度的节点电压状态向量并计算潮流分布,否则视为潮流不收敛。为减小迭代路径对潮流收敛性的影响,部分分析软件引用了PQ分解法次数变更策略。

对于大规模交直流混联电网,潮流数据不完整或不合理,如变压器分接头位置选择不当、线路电阻电抗过小以及电阻与电抗比值过大[9]、功率分布不合理,均有可能导致NR迭代的雅可比矩阵条件数过大,影响潮流收敛性。采用超/特高压交直流电网大容量、远距离输电,长线路重负荷在所难免,可能出现PV-PQ节点的频繁转换、直流控制策略切换[10]以及交直流间节点电压和等值负荷的频繁迭代,将进一步恶化潮流的收敛性,表现明显的病态特征,目前大量文献从理论上研究了病态潮流的求解和自动调整方法[11-14],但工程实用化可操作性不强。

调度和运行方式计算人员经常面临方式变化和调整,迫切需要提供翔实有用的潮流收敛性能和病态潮流的自动诊断和修正方法,当潮流方程组本身不存在实数解时,通过调整发电机出力、变压器分接头甚至切除部分负荷等措施使潮流方程回到可行解域,实现对大电网潮流数据的自动诊断和运行方式调整潮流计算。

本文针对上述问题,首先梳理总结了潮流收敛性特征及应对措施,分析了病态潮流的典型特征及产生原因,提出了病态潮流的诊断方法和潮流收敛性指标。然后,针对不收敛潮流方式,提出了基于内点法最优潮流的潮流收敛性自动调整方法。最后,针对大规模电网的运行方式调整潮流计算极易引起收敛问题,提出了一套工程实用的涵盖操作后不平衡功率分摊模拟、潮流数据检查、潮流初值给定、潮流收敛性自动识别、潮流方式自动调整的潮流计算方法。

1 病态潮流的特征及产生原因

如图1所示,随着负荷的增加,潮流方式收敛的电压解逐渐逼近电压崩溃点,潮流求解收敛性逐渐变差,需根据潮流收敛特征给出相应的求解方法。

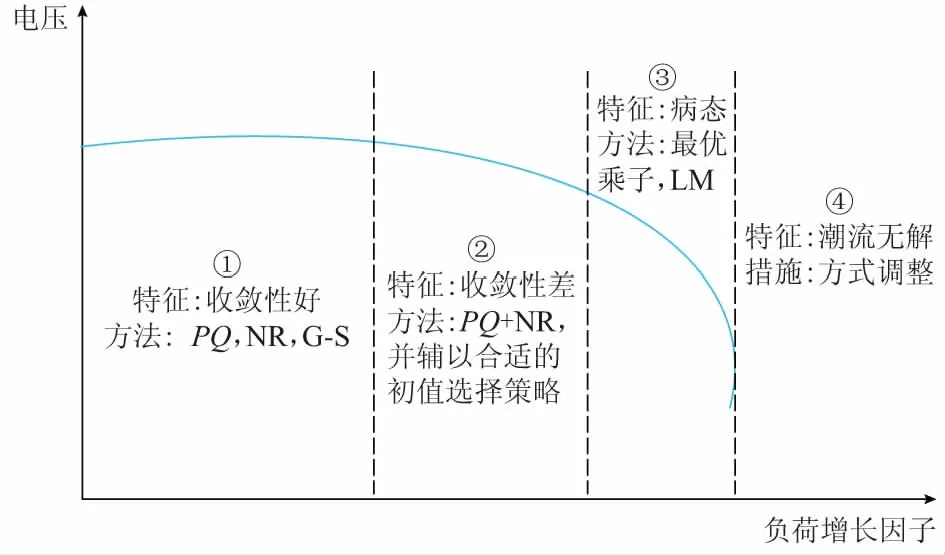
图1 潮流收敛性特征及应对措施Fig.1 Convergence characteristics of power flow and counter measures

病态潮流求解中表现的特征有:潮流收敛依赖于搜索路径和参数设置,潮流收敛解严重偏离启动初值,迭代次数增加而收敛速度慢。数学上表现为潮流解临近电压不稳定点,采用牛顿类方法求解时表现为雅可比矩阵中部分元素的微小变化或者不平衡向量的微小变化将引起修正解的很大变化。

引起潮流病态的主要原因:一是算法,如牛顿类方法迭代中雅可比矩阵条件数过大;二是潮流方式,如存在部分线路或断面潮流过重。

但工程实际中,调度方式运行人员更关注NR迭代中如何自动诊断潮流病态并快速调整潮流,以及实用的运行方式调整潮流计算方法。

2 病态潮流的诊断方法和潮流收敛性指标

对于NR迭代过程中出现的病态现象,理论上可以采用迭代中雅可比矩阵求条件数,并依据条件数判别潮流病态。但实际中因计算量和雅可比矩阵求逆困难,一般采用如下经验判别:①系数矩阵间数量级相差很大并无一定规则;②系数矩阵中某些行或列近似线性相关,或消去过程中出现小的主元素;③余量已经很小,但解不符合要求。

本文根据实际大型电网潮流计算采用简化NR法的计算经验,并考虑到最优乘子法[4,15]可以收敛得到最小二乘意义下的潮流解,能避免NR法潮流的发散和振荡现象,针对带最优乘子的NR迭代,采用如下病态潮流诊断方法。

设第k次迭代时[Δx](k)中电压幅值和相角最大元素的绝对值分别为ΔU(k)和Δδ(k),定义电压幅值和相角迭代衰减比指标分别为ΔU(k)/ΔU(k-1)和Δδ(k)/Δδ(k-1)。

依据ΔU(k)/ΔU(k-1)和Δδ(k)/Δδ(k-1)的衰减特性,进行潮流求解病态特性诊断。

ΔU(k)/ΔU(k-1)和Δδ(k)/Δδ(k-1)随着迭代次数增加,衰减趋近于0时,潮流具有较好的收敛性。若出现振荡时则潮流收敛性变差。若迭代过程中无法衰减趋近于0则潮流不收敛。

依据NR迭代中指标突变时ΔU(k)/ΔU(k-1)和Δδ(k)/Δδ(k-1)的大小,进行潮流求解的病态特征确定。当ΔU(k)/ΔU(k-1)大于Δδ(k)/Δδ(k-1)时,病态特征主因是局部无功支撑不足引起,反之,存在部分断面潮流过重引起的收敛问题。

若迭代过程中存在多次指标突变时,取各突变点ΔU(k)/ΔU(k-1)和Δδ(k)/Δδ(k-1)之和的大小进行病态特征确定。

带最优乘子的NR迭代,在避免潮流发散和振荡的同时,也避免了指标本身随NR迭代过程而波动振荡,总是表现为最小二乘解意义下的电压幅值和相角偏差,与已有的方法相比,提高了指标的实用性。

3 基于内点法最优潮流的潮流自动调整

对诊断识别为病态或无解的潮流方式,迫切需要实用的潮流自动调整方法,获取可行的潮流解。传统的非线性规划潮流调整,病态特征和可选调整区域未知,目标函数和可控变量选择困难,可控变量选择不当或可调空间不足时,均可能导致优化潮流不收敛。

以下根据病态特征的主因,提出了基于内点法[16]最优潮流的潮流自动调整方法。

3.1 局部无功支撑不足引起潮流不收敛

诊断病态特征主要是局部无功支撑不足时,一般在有功出力不调整的基础上,采用重新调整系统无功获取可行解。因此,选择调整发电机无功出力、投/切电容、电抗器组等各种控制变量,根据网损变化大小,选择1至2台机组有功出力可调,在满足系统各种约束的前提下,使系统中给定平衡网损变化的机组有功出力调整最小。其数学模型描述如下:

(1)

式中:PG0i和PGi分别为第i台机组调整前后的有功功率;SG为发电机组集合;wPG为对应机组的有功权重系数;h(x)表示决策变量x函数的等式约束,主要是指电力系统的网络和功率平衡约束;不等式约束g(x)为可控发电机无功出力、投/切电容、电抗器组的上下限运行约束。

根据[Δx](k)中电压幅值的偏差大小,选择偏差较大节点的发电机无功出力、投/切电容、电抗器作为可控变量。通常正偏差节点降无功出力,负偏差节点增无功出力。

3.2 断面潮流过重引起潮流不收敛

诊断病态特征主要是部分断面潮流过重时,需调整发电机有功出力,同时辅以局部无功调整,才能获取可行解。因此,选择调整发电机有功和无功出力等控制变量,在满足系统各种约束的前提下,使系统中所有可调机组的有功出力调整最小。数学模型描述同式(1),此时不等式约束为可控发电机有功出力和无功出力的上下限运行约束。

根据[Δx](k)中电压相角的偏差大小,选择偏差较大节点的发电机有功出力或负荷作为可控变量。通常正偏差节点有功降出力或增负荷,负偏差节点有功增出力或降负荷。

4 大规模电网运行方式调整潮流计算

对于运行人员调整后的电网运行方式,极易出现潮流收敛性问题。在本文提出的自动诊断潮流病态并快速调整潮流方法的基础上,结合并完善工程实用中的操作后不平衡功率分摊模拟、潮流数据检查、潮流初值给定方法,提出了一套工程实用的运行方式调整潮流计算方法,以满足对运行方式调整潮流计算的需求。

4.1 操作后不平衡功率ΔP的分摊模拟

针对大电网的运行方式调整包括网络拓扑调整和网络节点注入调整。对于网络节点注入调整引起的操作后不平衡功率,需事先按设定的规则,模拟操作后的功率平衡过程。

1)方法1:模拟发电机和负荷的一次频率响应

将操作后引起的不平衡功率ΔP按提供的机组调差系数和负荷频率响应特性,进行一次调频模拟分摊不平衡功率。

依据机组i调差系数Ri,节点n负荷PLn0和静态负荷频率变化1%引起有功变化百分比ln,则机组i和负荷节点n分别按式(2)和式(3)分摊不平衡功率:

(2)

(3)

若按式(2)分摊后,机组i出力越限,则固定该机组出力(一次调频能力失效),将剩余部分继续在仍具有一次调频能力的机组和负荷内部分摊。

2)方法2:模拟自动发电控制(AGC)机组二次调频响应

依据最终稳态分摊控制效果,具体分摊控制逻辑实现方法如下。

若某区域控制偏差(ACE)内区域I操作引起的功率缺额ΔPI可由区域I内的所有AGC机组j维持分摊平衡(如式(4)所示),则ΔPI仅在该ACE区内的AGC机组间分摊,此时频差为0。

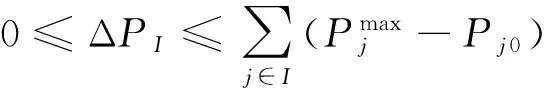
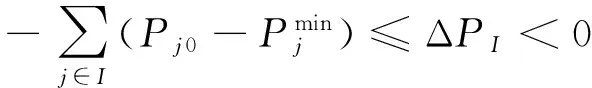
(4)

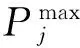
若某ACE内区域I操作引起的功率缺额ΔPI超过本ACE区内AGC机组的可调节范围(如式(5)或式(6)所示),此时区域I内AGC机组均分摊到上限或下限,超过部分由上一级调度管辖区S内的AGC机组参与分摊,最终实现频差为0。

(5)

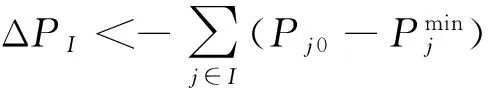
(6)

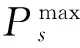
若某ACE内区域I操作引起的功率缺额ΔPI超过本ACE区内AGC机组和其上一级调度管辖AGC机组的可调节范围(如式(7)或式(8)所示),此时区内AGC机组和其上一级调度管辖AGC机组均分摊到限,超过部分由该网内其他ACE区内AGC机组一起参与有差调节，并依据各区的ACE确定各ACE区内的分摊量。

(7)

(8)

对于操作后不平衡功率分摊模拟后的方式潮流计算,单台平衡机可能存在出力越限,甚至因送出通道潮流过重而恶化潮流收敛性。可以通过后续潮流数据检查并给出相应的工程应对措施。

4.2 潮流数据检查及工程应对措施

小支路阻抗的检查:当线路电阻电抗过小时,导纳阵可能出现过大元素,引起雅可比矩阵条件数过大,恶化潮流收敛性。工程实用中小支路两端节点电压在数值上几乎接近,1×10-5以下的阻抗值与采用1×10-5阻抗值的计算,系统潮流结果差异可以接受。因此,采用小支路阻抗检查方法,潮流计算前对潮流数据进行检测。当小支路阻抗过小,小于设定最小阻抗值(如单精度计算时取1×10-5)时,则限定其为设定最小阻抗值。

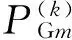
(9)

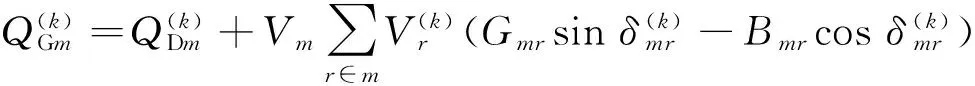
(10)

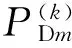
当校核存在明显越限时,对于不收敛的潮流方式,通过方式重新调整,基于内点法最优潮流可以消除平衡机送出线路潮流越限或选择候选机组模拟多平衡机分摊,实现平衡机出力越限调整,获取合理的潮流结果。

4.3 潮流初值给定

通常潮流计算基于平启动(V=V(0)),采用固定PQ分解法次数给出NR迭代潮流初值。当潮流初值不在NR迭代收敛域内时,NR迭代无法得到满足收敛的解。以下提出了变更PQ分解法次数和上轮NR迭代最优解加权的潮流初值给定方法,以改善与搜索路径强相关的潮流方式收敛性。具体方法如下。

若基于平启动采用固定PQ分解法次数确定NR初值,NR迭代结束后潮流不满足收敛条件。记NR迭代过程中的最优解记为V(k),当对应最优解V(k)的NR迭代功率偏差满足一定门槛值时,则下一轮基于平启动采用变更PQ分解法次数策略,取PQ分解法初值V(0)与V(k)加权,即V=αV(0)+βV(k)(α+β=1)作为下一轮NR迭代潮流初值。

由于本轮PQ+NR迭代时,计及了上轮NR迭代中的最优解V(k),可弥补PQ分解时的有功和无功功率的交互影响,给出更加合理的NR迭代潮流初值。

4.4 潮流病态和收敛性的自动识别

采用本文提出的病态潮流诊断电压幅值和相角迭代衰减比指标ΔU(k)/ΔU(k-1)和Δδ(k)/Δδ(k-1),自动识别病态潮流和迭代中的潮流收敛性。

若NR迭代过程中电压幅值和相角迭代衰减比指标随迭代次数的增加而振荡,均无法衰减趋近于0,则自动识别潮流求解表现病态,无法正常收敛。

当诊断潮流求解表现病态时,依据NR迭代中指标突变时ΔU(k)/ΔU(k-1)和Δδ(k)/Δδ(k-1)的大小,进行潮流求解的病态特征确定。当ΔU(k)/ΔU(k-1)大于Δδ(k)/Δδ(k-1)时,病态特征主因是局部无功支撑不足,反之,存在部分断面潮流过重引起收敛的问题。

4.5 潮流方式自动调整

对于潮流求解诊断为病态且确定了病态特征的潮流方式,采用本文提出的根据病态特征构建基于内点法最优潮流的潮流自动调整方法,通过优化方式进行出力或可投切电容电抗器调整,获取满足调整目标要求的潮流收敛方式。

大规模电网运行方式调整潮流计算流程见附录A图A1。

5 病态潮流诊断和运行方式调整潮流计算分析

5.1 病态潮流诊断指标及特征确定

以IEEE 14标准系统为例(选取发电机节点1为平衡机节点),发电机节点2出力增加为5倍的初始出力。负荷节点9,10,11,13,14均分别增加为4倍和5倍的初始负荷,此时潮流均不收敛。

采用本文病态潮流诊断指标定义,计算得到增加为4倍初始负荷无补偿和增加无功补偿(选择节点5增加)的两种方式下NR迭代的指标曲线,如图2所示。

由图2可知:负荷增加为4倍的初始负荷时,NR迭代到第2次时,较小的功率偏差向量导致大部分负荷节点电压大幅变化,随着迭代次数增加，病态潮流诊断指标出现振荡,且无法衰减趋近于0,潮流求解表现明显的病态特征。

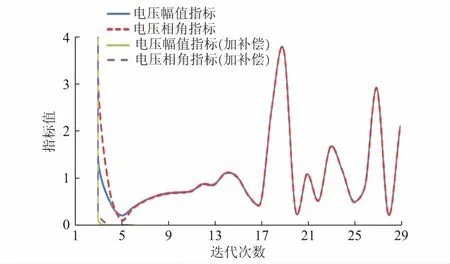
图2 NR迭代中病态潮流诊断指标(4倍初始负荷)Fig.2 Diagnostic indices of ill-conditioned power flow in each NR iteration step (four times of initial load)

将图2纵坐标最大值放大,以显示第2次NR迭代时指标突变点处的最大指标值(见图3)。

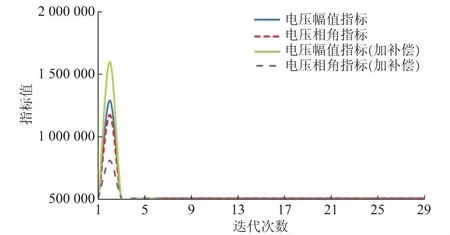
图3 NR迭代中指标突变点比较(4倍初始负荷)Fig.3 Jump point comparison of indices in NR iteration (four times of initial load)

依据指标衰减特性诊断潮流求解病态后,由图3中指标曲线突变处的指标大小确定病态特征。电压幅值指标大于电压相角指标,可以确定病态特征的主因是局部无功支撑不足。

图3中第2次NR迭代中电压幅值指标突变点处的值对应节点5的结果。若选择节点5增加无功补偿,如图2所示,随着迭代次数的增加,病态潮流诊断指标快速衰减趋近于0,具有较好的收敛性。

进一步将负荷节点9,10,11,13,14增加至5倍的初始负荷,依据指标衰减特性,随着迭代次数增加,指标无法衰减趋近于0,潮流不收敛,如图4所示。由图4可知,第2次和第27次NR迭代时存在指标突变(第2次NR迭代时相角指标值为1 688 295,幅值指标值为742 422,图4中未显示,突变情况同图3),均表现为相角指标大于幅值指标,潮流求解病态特征表现为部分断面潮流过重。

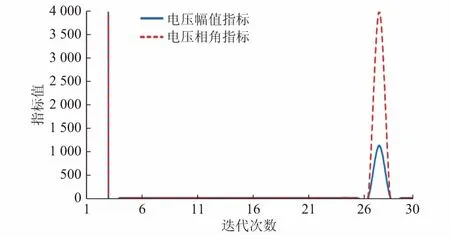
图4 NR迭代中病态潮流诊断指标(5倍初始负荷)Fig.4 Diagnostic indices of ill-conditioned power flow in each NR iteration step(five times of initial load)

同理,以西北电网某离线方式数据为例,交流节点数为9 672,支路数为23 428。该方式NR迭代的指标曲线如图5所示。在指标曲线各突变点处,电压幅值指标大于电压相角指标,潮流求解表现出局部无功支撑不足的病态特征。其中,横坐标为NR迭代次数,纵坐标为病态潮流诊断指标。

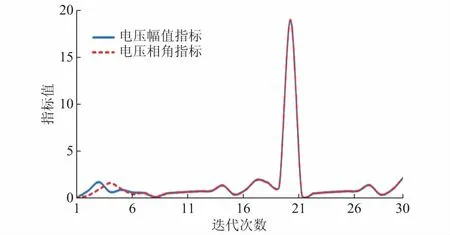
图5 NR迭代中病态潮流诊断指标(西北电网)Fig.5 Diagnostic indices of ill-conditioned power flow in each NR iteration step (Northwest grid)

指标曲线各突变点处NR迭代各节点的ΔU(k)/ΔU(k-1)和Δδ(k)/Δδ(k-1),反映了该节点前后两次迭代的电压幅值和相角的变化。病态特征主因是疆电外送通道传输功率大而通道无功支撑不足。

选取NR迭代第3次时电压幅值突变最大节点的近区变压器高压侧节点(甘肃桥湾风电场汇聚节点,补偿1 500 Mvar)进行无功补偿,此时潮流收敛。选取NR迭代第4次时电压相角突变正的最大节点和负的最大节点所在区域新疆和宁夏降低和增加出力(新疆外送出力减少2 000 MW),减少新疆外送使得甘肃桥湾风电场近区电压降落减少,此时潮流收敛。

从以上2个测试案例可知,采用本文提出的病态潮流诊断电压幅值和相角迭代衰减比指标,在快速诊断潮流病态及病态特征的同时,也给出了潮流调整的可行方向和可调区域。

5.2 平衡机出力越限检查及候选平衡机分摊

以某区域系统日计划数据为例,由于直流送电计划未及时更新,部分直流异步互联网络数据无法拼接,实际拼接网络数据中交流节点数为2 959,支路数为3 483。未拼接成功的异步互联直流可以分别等效模拟整流和逆变侧子网的机组增出力和负荷增加方式调整,两子网平衡机分别存在出力越上下限现象,某些断面时刻运行方式数据甚至出现潮流不收敛。

对某断面时刻不收敛方式,采用本文提出的平衡机出力越限检查及候选平衡机分摊方法后,如图6所示,NR迭代3次,此时2个异步子网的平衡机有功出力越限完全消除,越限部分已由候选平衡机在迭代中分摊,各子网分摊的总量趋于常量,NR迭代15次后所有节点累计的功率偏差趋近于0,潮流满足收敛条件。其中,横坐标为NR迭代次数,纵坐标为有功分摊量/功率偏差。

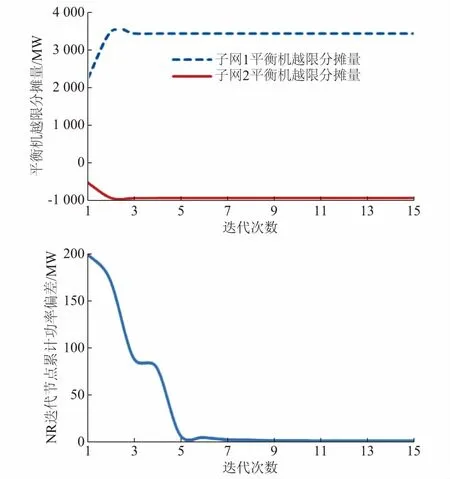
图6 NR迭代中平衡机越限分摊量和功率偏差曲线Fig.6 Allocation of balancing machine output limits and power deviation during NR iteration

5.3 局部无功支撑不足调整

继续退出部分直流受端换流站无功补偿容量时,此时受端无功支撑不足,甚至出现潮流不收敛。采用本文提出的病态潮流诊断方法,基于内点法最优潮流的潮流自动调整方法,尽量选择电压幅值突变较大节点所在区域的发电机无功出力和可投切电容电抗器作为控制量,以发电机出力调整量最小为目标(即有功网损变化最小),进行无功优化,结果如表1所示。

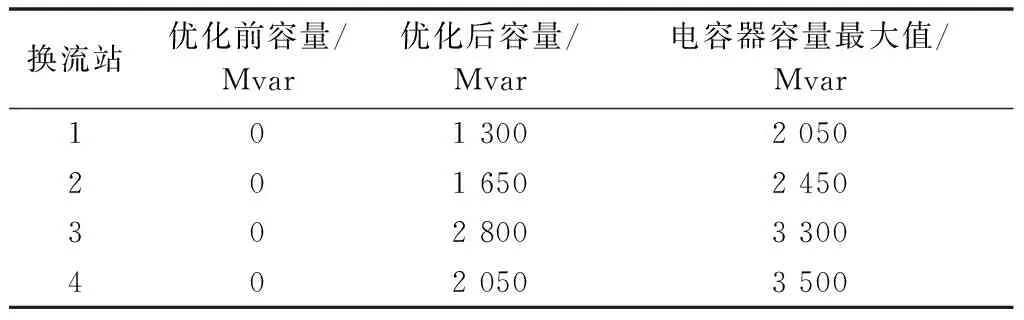
表1 无功优化前后主要投切点容量变化Table 1 Capacity change of switching node beforeand after reactive power optimization

5.4 断面潮流过重调整

继续降低某省外送部分直流输电容量并仅减弱交流送出通道电气联系,此时外送交流断面潮流过重,常规潮流程序计算出现潮流不收敛。采用本文提出的病态潮流诊断方法,基于内点法最优潮流的潮流自动调整方法,尽量选择电压相角突变数值较大的正负节点所在区域发电机有功出力作为控制量(本例对应为部分省内和省外机组),以发电机出力调整量最小为目标,进行最优潮流优化,结果如下:省内和省外发电机出力优化后的调整总量分别为-616 MW和859 MW。

优化后单回500 kV交流线路送电2 600 MW(较初始数据单回线路增加1 800 MW),较初始数据交直流6回线路外送断面功率回降616 MW,省外受电侧机组增出力859 MW,多余部分弥补单回500 kV交流线路传输功率增加1 800 MW引起的线路传输网损的急剧增加。

6 结语

本文采用带最优乘子的NR迭代电压幅值和相角的偏差衰减比来诊断病态潮流,根据两者突变点处的大小确定病态特征,建立基于内点法最优潮流的病态潮流和无解潮流的自动调整模型。最后,针对大规模电网运行方式调整潮流计算,提出了一套工程实用的操作后不平衡功率分摊模拟、潮流数据检查、潮流初值给定、潮流收敛性自动识别、潮流方式自动调整的方法。仿真分析结果表明,本文提出的病态特征诊断和运行方式自动调整方法,能准确有效地识别潮流病态特性,有助于潮流自动调整及收敛性改善,并应用于江苏智能电网调度控制系统(简称“D5000系统”)运行方式调整潮流计算。

随着交直流电网中电力电子设备的增加,大规模交直流电网的互联,所提潮流诊断和调整方法如何更好地适应两者的影响,仍需进一步深入研究和讨论。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] TINNEY W F. Power flow solution by Newtons method[J]. IEEE Transactions on Power Apparatus and Systems, 1967, 86(11): 1449-1449.

[2] STOTT B. Effective starting process for Newton-Raphson load flows[J]. Proceedings of the Institution of Electrical Engineers, 1971, 118(8): 983-987.

[3] WARD J B, HALE H W. Digital computer solution of power-flow problems[J]. Transactions of the American Institute of Electrical Engineers: Part Ⅲ Power Apparatus and Systems, 1956, 75(3): 398-404.

[4] IWAMOTO S, TAMURA Y. A load flow calculation method for ill-conditioned power systems[J]. IEEE Transactions on Power Apparatus and Systems, 1981, 100(4): 1736-1743.

[5] BOUARICHA A, SCHNABEL R B. Tensor methods for large sparse systems of nonlinear equations[J]. Mathematical Programming, 1998, 82(3): 377-400.

[6] SALGADO R S, ZEITUNE A F. Power flow solutions through tensor methods[J]. IET Generation, Transmission & Distribution, 2009, 3(5): 413-424.

[7] LAGACE P J. Power flow methods for improving convergence[C]// 38th Annual Conference of the IEEE Industrial Electronics Society, October 25-28, 2012, Montreal, Canada: 1387-1392.

[8] 严正,范翔,赵文恺,等.自适应Levenberg-Marquardt方法提高潮流计算收敛性[J].中国电机工程学报,2015,35(8):1909-1918.

YAN Zheng, FAN Xiang, ZHAO Wenkai, et al. Improving the convergence of power flow calculation by a self-adaptive Levenberg-Marquardt method[J]. Proceedings of the CSEE, 2015, 35(8): 1909-1918.

[9] 姚玉斌,鲁宝春,陈学允.小阻抗支路对牛顿法潮流的影响及其处理方法[J].电网技术,1999,23(9):27-31.

YAO Yubin, LU Baochun, CHEN Xueyun. A method to deal with the effect of small impedance branches to prevent divergence in newton raphson load flow[J]. Power System Technology, 1999, 23(9): 27-31.

[10] 杨堤,程浩忠,姚良忠,等.基于电压控制特性的电压源型多端直流/交流系统潮流求解[J].电力系统自动化,2016,40(6):42-48.DOI:10.7500/AEPS20150310015.

YANG Di, CHENG Haozhong, YAO Liangzhong, et al. Power flow solving of VSC multi-terminal DC/AC system based on voltage control characteristics[J]. Automation of Electric Power Systems, 2016, 40(6): 42-48. DOI: 10.7500/AEPS20150310015.

[11] 王宪荣,包丽明,柳焯.极坐标系准最优乘子潮流解法研究[J].中国电机工程学报,1994,14(1):40-45.

WANG Xianrong, BAO Liming, LIU Zhuo. The study of ill-conditioned load flow using quasi-optimal factor in polar coordinates[J]. Proceedings of the CSEE, 1994, 14(1): 40-45.

[12] 李智欢,韩云飞,苏寅生,等.基于节点类型转换的潮流收敛性调整方法[J].电力系统自动化,2015,39(7):188-193.DOI:10.7500/AEPS20140916001.

LI Zhihuan, HAN Yunfei, SU Yinsheng, et al. A convergence adjustment method of power flow based on node type switching[J]. Automation of Electric Power Systems, 2015, 39(7): 188-193. DOI: 10.7500/AEPS20140916001.

[13] 张跃驰,刘本希,罗彬,等.基于PSD-BPA的电网运行方式数据自动整合与调整方法[J].电力系统自动化,2017,41(1):102-108.DOI:10.7500/AEPS20160302004.

ZHANG Yuechi, LIU Benxi, LUO Bin, et al. PSD-BPA based automatic integration and adjustment method of power grid operation plan data[J]. Automation of Electric Power Systems, 2017, 41(1): 102-108. DOI: 10.7500/AEPS20160302004.

[14] 李敏,陈金富,陈海焱,等.一类潮流计算无解的实用性调整研究[J].电力系统自动化,2006,30(8):11-15.

LI Min, CHEN Jinfu, CHEN Haiyan, et al. Load flow regulation for unsolvable cases in a power system[J]. Automation of Electric Power Systems, 2006, 30(8): 11-15.

[15] 胡泽春,严正.带最优乘子牛顿法在交直流系统潮流计算中的应用[J].电力系统自动化,2009,33(9):26-31.

HU Zechun, YAN Zheng. Application of newton load flow methods with optimal multiplier for AC/DC power systems[J]. Automation of Electric Power Systems, 2009, 33(9): 26-31.

[16] WEI H, SASAKI H, YOKOYAMA R. An application of interior point quadratic programming algorithm to power system optimization problems[J]. IEEE Transactions on Power Systems, 1996, 11(1): 260-267.

[17] 杜正春,王延延,王毅,等.获取电力系统运行方式的多平衡机潮流模型[J].电力系统自动化,2014,38(16):41-46.DOI:10.7500/AEPS20130617008.

DU Zhengchun, WANG Yanyan, WANG Yi, et al. Multi-balancing machine load flow models for obtaining power system operation mode[J]. Automation of Electric Power Systems, 2014, 38(16): 41-46. DOI: 10.7500/AEPS20130617008.

彭慧敏(1972—),男,通信作者,博士,高级工程师,主要研究方向:电力系统分析与控制。E-mail： penghuimin@sgepri.sgcc.com.cn

李 峰(1981—),男,高级工程师,主要研究方向:电力系统分析与控制。E-mail: lifeng@sgepri.sgcc.com.cn

袁虎玲(1985—),女,高级工程师,主要研究方向:电力系统分析与控制。E-mail: yuanhuling@sgepri.sgcc.com.cn

(编辑蔡静雯)

( continuedonpage159)( continuedfrompage142)