改善独立微网频率动态特性的虚拟同步发电机模型预测控制

陈来军, 王 任, 郑天文, 司 杨, 梅生伟

(1. 青海省清洁能源高效利用重点实验室(青海大学新能源光伏产业研究中心), 青海省西宁市810016;2. 电力系统及发电设备控制和仿真国家重点实验室(清华大学), 北京市100084)

0 引言

作为分布式能源的有效利用形式,微网技术自提出后便引起了广泛关注[1-3]。微网是由分布式电源、储能装置、变流器、负荷及监控保护装置等有机整合在一起的小型发配电系统,具有并网运行和孤岛运行两种模式[4-6]。孤岛模式下,由于失去大电网支撑,微网需要依靠自身内部各单元维持系统电压和频率;在稳态时使其保持为额定值,暂态时则需将其波动限制在安全范围内。因此,需要对各微电源进行协调控制,从而保证独立微网的安全稳定运行[7-8]。

在微网中,分布式电源一般通过逆变器接入,常见的控制策略为恒功率控制、下垂控制等[9-10]。其中,下垂控制因其即插即用、无需通信的优点而应用广泛。然而,采用下垂控制的逆变器对系统惯量贡献甚微,当分布式电源比例逐渐增加时,微网惯量随之降低,稳定性减弱。另一方面,可再生能源出力受自然条件影响,具有随机性和波动性,且孤网模式下,分布式电源和负荷数量较少,单机或单个负荷所占容量比例大,因此,无论是电源出力波动或负荷投切,均可能会引起微网内较大程度的功率失衡[11],进而造成频率波动。当系统惯性较弱时,频率波动幅值极易超过安全阈值,影响逆变器设备或频率敏感型负荷的安全运行,甚至触发频率保护装置动作,导致切机切负荷。而某些重要电源或关键负荷的退出运行将会加剧功率的不平衡,严重情况下可能造成系统崩溃。因此,一方面,需要增强系统惯量水平;另一方面,需要协调控制各微电源出力,及时消除功率差额,以提升系统频率动态特性。

针对系统惯性不足的问题,不少学者将惯量的思想引入逆变器的控制中,提出了虚拟同步发电机(VSG)的控制策略[12-13]。文献[14]提出了电流源型VSG的概念,但其在独立微网中适应性不强。为了扩大逆变电源的适用范围,学者们提出了电压源型VSG的控制方法[15-17]。通过模拟同步发电机的转子方程和一次调频特性,使所提控制方法能够用于孤岛运行模式,并在一定程度上提高了系统稳定性。文献[18]将VSG运用于孤立微网的频率控制,改善了系统的频率特性。文献[19]对储能装置采用虚拟同步控制策略,其出力大小为频差和频率微分的线性组合,两者的权重系数通过实时计算并自适应调整,有效地减弱了负荷投切和风电出力波动引起的频率变化。文献[20]对储能装置采用VSG控制策略,提升了光储柴独立微网的频率稳定性,并给出了相关参数的整定方法。

在上述的VSG方案中,有功功率—频率控制中的指令功率一般保持不变,因此其主要参与惯性调节和一次调频,在二次调频过程中贡献甚微。如果二次调频仅由柴油发电机承担,当可再生能源渗透率较高时,可能导致频差偏移过大。有鉴于此,本文提出一种基于模型预测控制(MPC)的VSG控制方法,根据系统当前运行状态,求解满足频率约束的优化模型,得出系统所需的功率增量,并将此结果用于VSG指令功率调整,使其辅助柴油发电机进行微网二次调频,减小暂态过程中的频率偏移。最后,通过仿真对比,验证了所提控制策略的有效性。

1 问题描述

1.1 独立微网拓扑

独立微网一般由微电源、负荷及储能装置组成,典型拓扑结构参见附录A图A1。图中,微电源主要包括柴油发电机、光伏发电系统及储能型VSG。柴油发电机通过变压器接至交流母线,为系统提供电压和频率参考;光伏系统采用最大功率点跟踪控制方法以最大化利用光伏发电;储能装置与逆变器构成VSG接入,当系统功率失衡时及时平衡功率,以减弱频率波动。

1.2 VSG模型及控制

VSG拓扑结构参见附录A图A2。其中,Udc为VSG直流侧电压;uo=[uoa,uob,uoc]T和i=[ia,ib,ic]T分别为VSG的输出电压和电流;e=[ea,eb,ec]T为经滤波后的电压;u=[ua,ub,uc]T为电网电压;LS和RS分别为滤波电感和电阻;Lg和Rg分别为线路电感和电阻。

VSG的有功频率控制模拟同步发电机的转子方程,控制框图参见附录A图A3。图中:Pm和Pe分别为VSG的输入和输出有功功率;ω为系统的角频率;ω0为额定角频率;M为虚拟惯量;D为阻尼系数。与上述控制框图对应的传递函数和同步发电机的转子方程类似,有

(1)

由式(1)可知,M模拟了转动惯量,可以减缓扰动后系统的频率波动,且有功功率—频率控制具有一次调频的作用。然而,一次调频为有差调节,为使频率恢复至额定值,一般需进行二次调频。虽然柴油发电机可用于二次调频,但其调节速度较慢,可能无法满足系统需求。作为电力电子设备,VSG响应速度快,因此可以通过调整Pm的大小,使频率恢复至额定值。另一方面,根据系统受扰后频率变化情况实时调整VSG出力,可以改善暂态过程中频率响应特性。

2 基于VSG的MPC

2.1 MPC原理

MPC算法基本思想是:首先将系统离散化,再结合系统当前时刻状态及控制量,预测未来p个周期内系统的状态,然后根据期望值求取当前时刻的最优控制量。具体过程可用图1加以说明[21]。

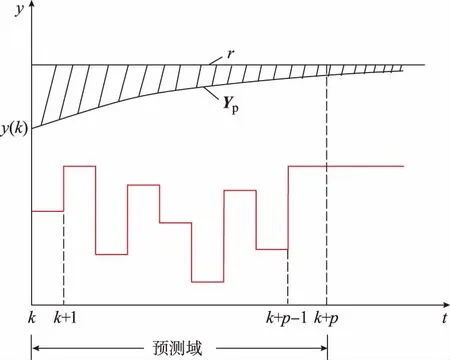
图1 MPC过程Fig.1 Process of MPC

图1中,y(k)为k时刻系统输出,基于系统传递函数,可得系统起于y(k)的未来一段时间内的输出,记为

Yp(k+1|k)=

[yp(k+1|k)yp(k+2|k) …yp(k+p|k)]

(2)

式中:下标p表示预测域。

此外,预测系统未来输出还需预测域内的控制输入,即

Uk=

[u(k|k)u(k+1|k) …u(k+p-1|k)]

(3)

这也正是将要求解的优化变量。

控制目标是使系统输出与参考值r(·)的偏差趋于零,同时满足系统约束条件。即

(4)

其中

(5)

式(4)的解为:

[u*(k|k)u*(k+1|k) …u*(k+p-1|k)]

(6)

将其第1个分量作用于系统,在k+1时刻,以新得到的测量量y(k+1)作为初始条件,重新计算式(4)。因此,MPC可概括为:在每个采样周期用最新的测量值更新优化问题,并将得到的解的第1个分量作用于系统,如此循环进行。

2.2 VSG的预测模型

式(1)所示的VSG控制方程可改写为:

(7)

式中:ω′=ω-ω0；Tm=Pm/ω;Te=Pe/ω。

一般地,分布式电源出力波动或负荷投切会造成功率供需失衡,将引发系统频率波动,进一步使VSG输出电压和系统母线电压功角差改变,造成VSG输出功率发生变化。因此,对于VSG而言,可将Te视为扰动量,将VSG的功率设定值Pm视为控制输入。在实际运行中,系统频率变化不大,则可认为ω≈ω0。因此,Tm和Pm是线性关系,亦可将Tm作为输入。

将式(7)转化为离散模型:

ω′(k+1)=Aω′(k)+BuTm(k)+BdTe(k)

(8)

其中

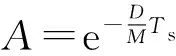
式中:Ts为系统采样时间。

进而将式(8)改为增量模型,即

Δω′(k+1)=AΔω′(k)+BuΔTm(k)+BdΔTe(k)

(9)

式中：Δω′(k)为被控输出量,其物理意义为系统角频率变化率。

根据MPC基本原理,带约束的MPC优化问题可描述为:

(10)

式中:i=0, 1,…,p;Δω′(k)为k时刻实际测量值;ω′(k+i|k)为i时刻的角频率差,因此与之对应的参考值可选为零;Δω′(k+i|k)为控制输出,表示i时刻的系统角频率变化率;ΔUk为预测域内控制输入的增量表达式,即

ΔUk=

[ΔTm(k|k)ΔTm(k+1|k)…ΔTm(k+p-1|k)]

(11)

性能指标主要包含系统频差和VSG出力两个部分,即

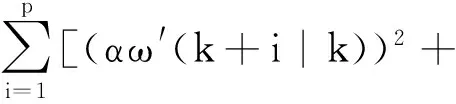
(βΔTm(k+i-1))2]

(12)

式中:α和β分别为系统角频率差和VSG出力的权重系数。

权重系数的大小表征了性能指标中各个目标项的重要程度,选取合适的权重系数对整体的控制效果具有重要意义。然而,权重系数的选取一直是MPC的一个难点,至今没有统一和有效的理论指导权重系数的选取,主观经验依旧起主导作用[22]。但就本文的研究而言,性能指标有两项,即系统角频率的偏差和VSG的输入转矩,前者的作用是使角频率尽快恢复,后者的作用是尽可能减少VSG调节成本。借鉴已有的研究成果[23],权重系数可基于以下原则进行选取:角频率偏差与其权重系数相乘后的数值应该和VSG输入转矩差与其权重系数相乘后的数值大小相当,即αω′≈βΔTm,否则,如果αω′≪βΔTm,性能指标主要目标是减小VSG的出力成本,那么系统频率可能无法快速恢复;反之,如果αω′≫βΔTm,性能指标的主要目标是使系统频率恢复,而不考虑VSG的出力成本,可能无法做到资源的合理利用,甚至因其出力调节的变化率过快而威胁系统稳定性。据此可进行权重系数的合理选取。

3 控制策略设计与分析

3.1 控制系统总体架构

根据微网频率波动情况,利用MPC算法计算出能够提升频率动态特性的功率增量,以此来改变VSG输入功率设定值。系统的控制框图见图2。

图2中,锁相环用于采集当前时刻系统角频率信号,互感器量测的电压电流用于计算输出功率。结合VSG当前输入值Pm,可计算出下一时刻的输入增量ΔTm,将其转化为ΔPm用于VSG控制,产生电压参考信号驱动逆变器工作。

MPC算法和VSG控制构成一个闭环控制系统,即MPC-VSG。两者的交互具体表现为VSG的输出功率Pe和电网频率f是MPC算法的输入,MPC算法的输出是VSG指令功率的增量。电网频率f增加时,VSG与系统功角差变小,VSG输出功率Pe变小。当f变大,Pe变小时,经过MPC算法计算后,输出为一负值,即减小了VSG的功率输入设定值,进而使VSG输出功率减小,电网频率随之降低;反之亦然。因此,上述MPC-VSG控制可有效抑制系统频率的变化。

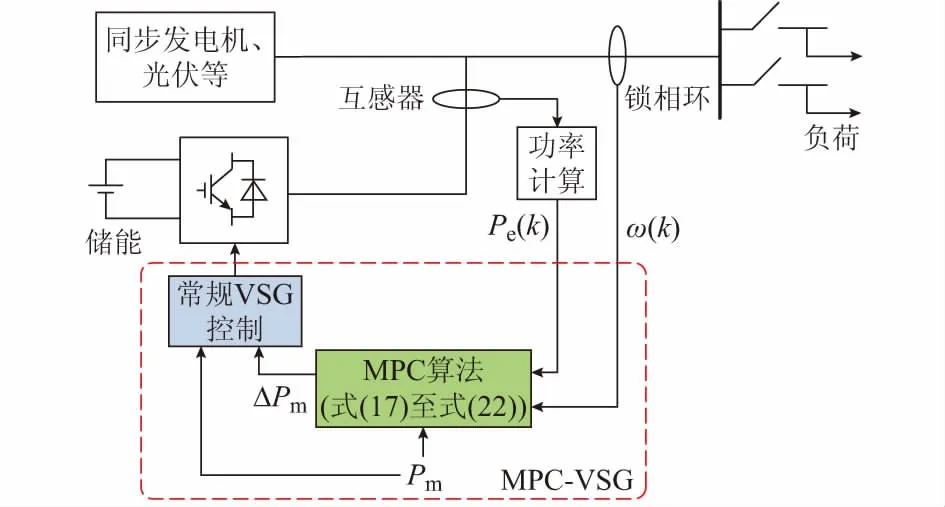
图2 系统控制框图Fig.2 System control diagram

3.2 控制策略求解

为了求解式(10),可先将其化为二次规划的标准形式。该模型中优化变量为ΔUk,若能将目标函数化为二次标准型,同时将不等式约束改写成CΔUk≤b的线性标准形式,则可用内点法进行求解[21]。

首先,计算式(10)对应的预测输出量Yp(k+1|k)。根据式(2)中对预测输出量的定义及式(10)中第1个式子可推导得出Yp,ω(k+1|k)的表达式为:

Yp,ω(k+1|k)=

[ω′(k+1|k)ω′(k+2|k) …ω′(k+p|k)]=

SωΔω′(k)+γω′(k)+SuΔUk+SdΔd(k)

(13)

分析可知,预测域的选取过大,会加重计算负担,可能无法实现在线求解控制率,而预测域选取过小,可能会造成控制不精确,影响控制效果。本文预测域的选取参考文献[24],式(13)中各系数为:

(14)

根据式(12)可得目标函数表达式为:

J(ω′(k),ΔUk)=‖ΓωYp,ω(k+1|k)‖2+

‖ΓuΔUk‖2

(15)

式中:Γω和Γu分别为角频率差和VSG出力的权重系数矩阵,即Γω=diag(α,α,α),Γu=diag(β,β,β)。

定义中间变量:

Ep(k+1|k)≜-SωΔω′(k)-γω′(k)-SdΔd(k)

(16)

将式(13)代入(15)可得:

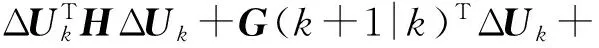
(17)

(18)

对于控制输出的约束,可将其转化为Cz≤b的形式,定义控制输出量为:

Yc(k+1|k)=

[Δω′(k+1|k) Δω′(k+2|k) Δω′(k+3|k)]

(19)

推导可知:

Yc(k+1|k)=Sω,cΔω(k)+Su,cΔUk+Sd,cΔd(k)

(20)

(21)

因此,控制输出约束可表示为:

(22)

综合上述分析,可得到如图3所示的控制策略流程。

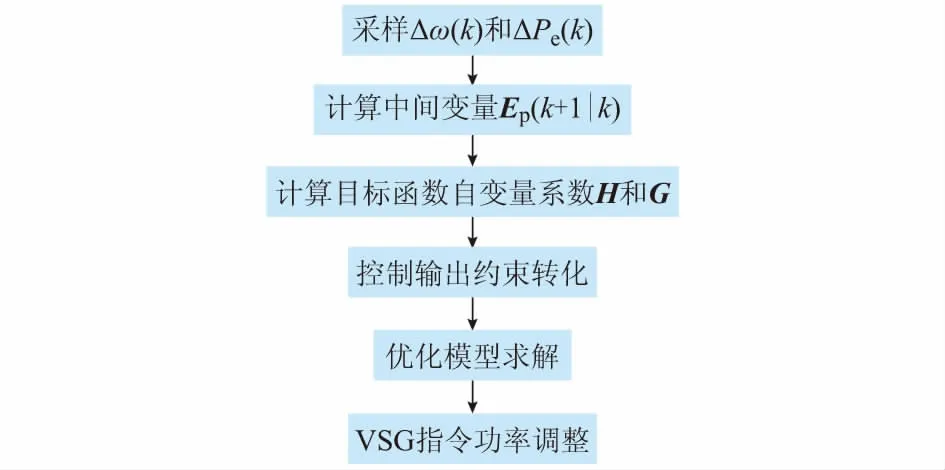
图3 控制策略流程图Fig.3 Flow chart of control strategy

3.3 控制策略分析

VSG的输入功率设定值来自于模型预测算法计算的结果,算法的稳定性将直接影响控制策略的效果。而分析算法稳定性的关键在于将模型预测算法得到的结果作为VSG的功率输入设定值代入系统状态方程,校验微网频率是否能够恢复。

模型预测算法所提模型为有约束的离散模型。由于约束的存在,式(17)难以直接获得控制律的解析表达式,为了分析算法稳定性,可分情况讨论。

1)当式(17)的解落在可行域的边界内,即式(22)取小于号时,原模型退化为一个无约束模型,由式(17)可计算出控制率为:

(23)

用于调整VSG功率输入的控制量为:

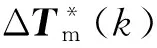
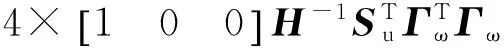
KEp(k+1|k)

(24)

将式(24)代入式(10)中的第1个式子可得:

Δω′(k+1)=(A-BuKSω)Δω′(k)-

BuKγω′(k)+(Bd-BuKSd)Δd(k)

(25)

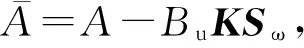
(26)

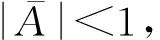
2)当式(17)的解达到约束边界,即式(22)取等号时,MPC算法得出的VSG的输入功率设定值将为允许范围内VSG的出力上限。此时,VSG按照此上限值输出有功功率,微网频率的变化情况将主要由系统内其他机组及储能装置的调节作用决定。

综上,本文所采用的MPC算法能够保证VSG在微网出现扰动后,能够基于减小频率变化率和频率偏差的原则,迅速调整自身输出功率,以提升频率响应特性。

4 仿真分析

4.1 仿真工况

在MATLAB/Simulink软件环境下对上述控制策略进行测试,仿真算例的拓扑结构如图1所示。柴油发电机采用二阶模型[16,18],调速器结构及控制参考文献[20, 25]进行设计,具体控制参数见附录B表B1。光伏发电系统采用最大功率点跟踪控制[26],按照算法计算出的功率指令向微网注入功率,其大小受外界条件影响。VSG容量为10 kVA,具体控制参数见附录B表B2。

MPC为离散系统,结合系统复杂程度及MATLAB计算能力,采样周期取为Ts=100 μs;约束条件中,角频率的变化率阈值可参考ISO标准8525-5,即|Δω′(k)|≤2π×0.6/10 000。

结合本文仿真中工况,系统频差的变化的上限大约为0.2 Hz,折合成角频率约为1.26 rad/s,而VSG可调整出力的变化上限为4～5 kW,折合成转矩约为13 N·m。角频率偏差上限数值约为VSG可调整出力上限数值的10倍,因此可以选择β=1,α=10β=10。

4.2 算例分析

仿真算例包含两部分,分别测试在负荷投切和光伏电源出力波动两种情况下,本文所提的MPC-VSG控制策略和常规VSG控制方法[17-18]两种模式下系统频率的变化及各电源的出力情况。

1)负荷投切

仿真时长为50 s。初始时刻,柴油发电机和光伏出力分别为15 kW和6 kW,VSG出力为5 kW,总负荷为26 kW,系统功率平衡,频率稳定于50 Hz。t=5 s时刻,投入5 kW负荷,t=25 s时刻,切除5 kW负荷。图4(a)和图4(b)分别给出了两种不同控制模式下系统频率变化和各电源出力情况。

由图4(a)可知:当负荷突然接入或切除时,系统出现功率不平衡,频率发生相应变化。若采用传统的控制方法,系统频率波动最大值约为0.34 Hz,超过安全阈值;而MPC下系统频率波动最大值仅为0.2 Hz,振荡幅值减小至原来的58.8%,且频率变化速度变慢。从图4(b)可以看出,当VSG采用MPC方法时,其出力能够较快响应负荷投切引起的功率失衡,同步发电机出力调整速度变慢,调节负担变小。

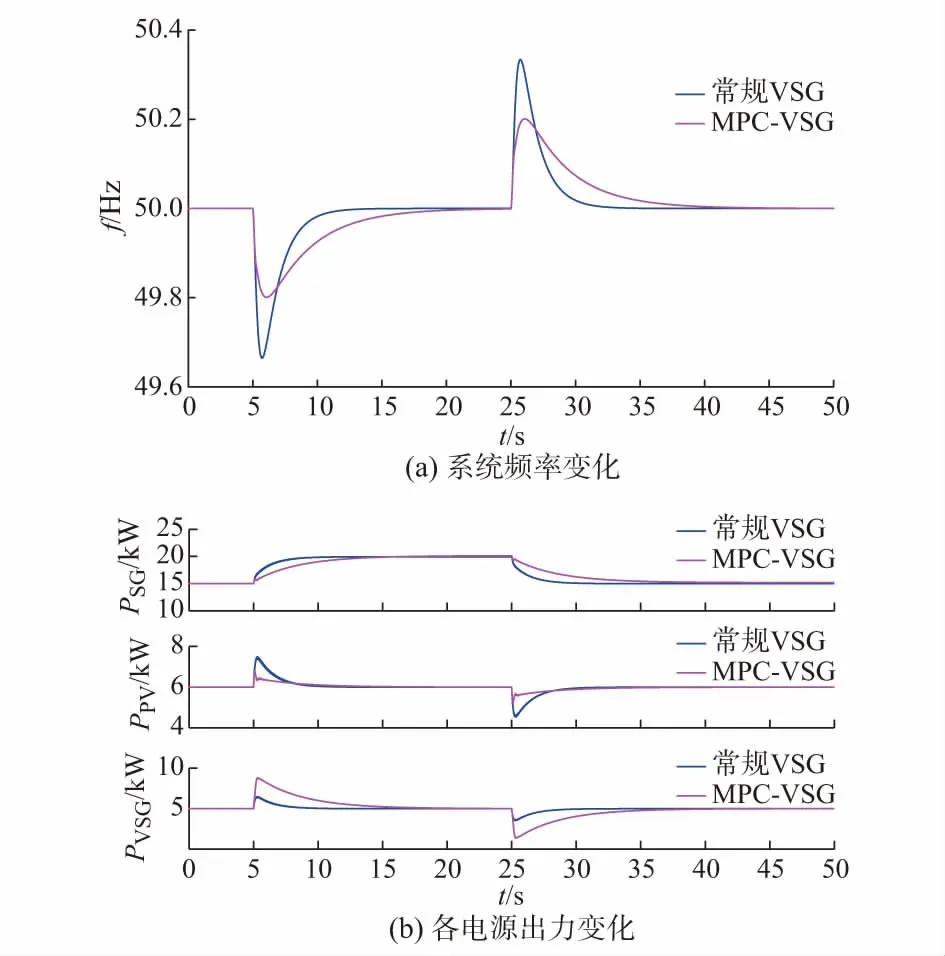
图4 负荷投切时仿真波形Fig.4 Simulation waveforms in load switching

2)光伏出力波动

仿真时长设定为50 s,柴油发电机和光伏出力分别为15 kW和10 kW,VSG出力为5 kW, 系统总负荷为30 kW。光伏电源按照最大功率点跟踪控制,其输入功率变化采用EN50530标准[27],t=5～16 s期间,光照减弱光伏输入功率出现暂降,t=16 s时刻以后,光照恢复正常。其功率输入见附录B图B1。

图5(a)和图5(b)比较了MPC和传统控制模式下,系统频率和各电源的出力情况。

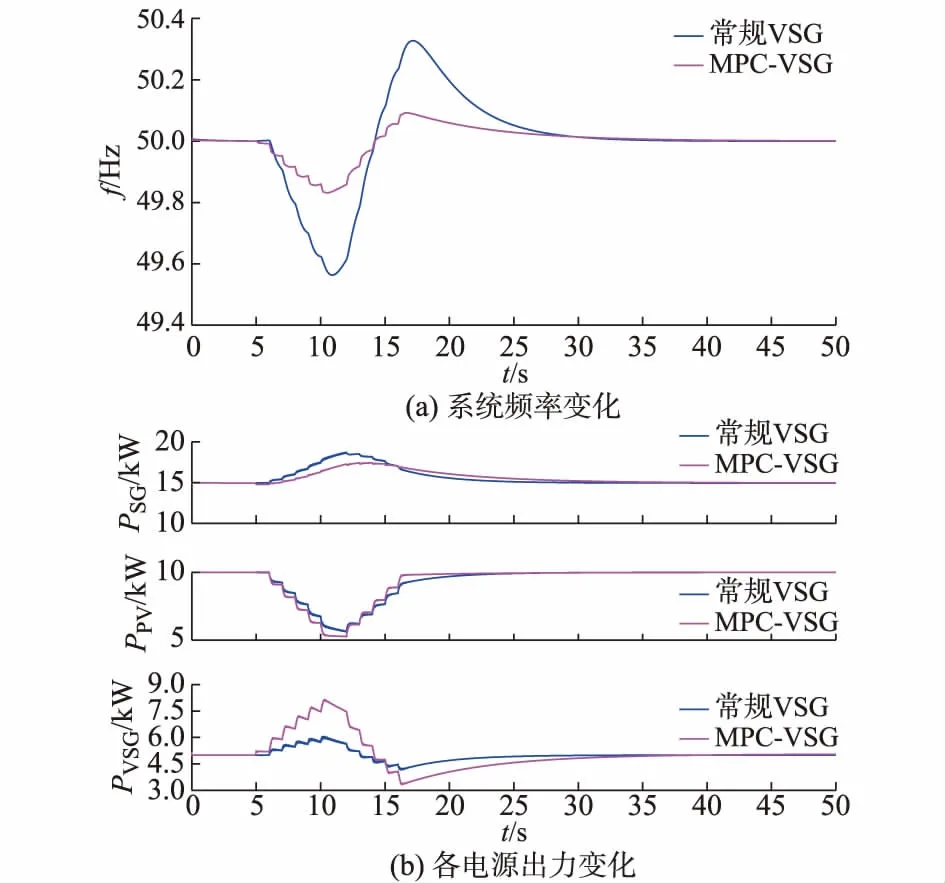
图5 光伏出力波动时仿真波形Fig.5 Simulation waveforms in PV output fluctuation

由图5可知,当天气条件变化引起光照强度改变时,光伏出力发生相应的变化。采用传统控制时,系统频率波动幅值约为0.45 Hz,而采用MPC-VSG时,频率波动幅值减小至0.16 Hz,频率动态特性得到显著提升,且同步发电机的出力波动幅值减小。

从上述两种工况的仿真结果可以看出,由于可再生能源出力波动或负荷投切等因素造成微网内功率不平衡时,微网频率出现明显波动。与传统控制方法相比,MPC模式下的VSG能够较快跟踪系统功率变化,通过调整自身出力及时平衡功率,从而改善暂态过程中频率动态特性,同时减小了其他电源的调频负担,提高了系统的稳定性能。

5 结语

针对独立微网内负荷投切或光伏出力波动导致系统功率失衡,引起频率振荡甚至超过安全阈值的问题,本文提出一种基于MPC的VSG控制策略。首先建立了VSG频率调节的预测模型,在此基础上,设计了利用预测模型计算能够提升微网频率动态特性的功率增量,并将其用于VSG出力调整的控制策略。通过对控制率求解算法收敛性的分析,为关键参数的选取提供了依据。两种典型工况的仿真结果表明,在所提控制策略下,VSG能够迅速调整自身出力,响应系统功率变化,从而将频率波动限制在安全范围内,改善了系统的频率动态特性。

值得一提的是,目前本文主要通过理论和仿真分析对所提控制策略的正确性和有效性进行了验证,在今后的研究中,还将对控制策略进行有效的实验测试,以促进其应用于工程实际。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] LASSETER R H. Microgrids[C]// Power Engineering Society Winter Meeting, January 27-31, 2002, New York, USA: 305-308.

[2] POGAKU N, PRODANOVIC M, GREEN T C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 613-625.

[3] 鲁宗相,王彩霞,闵勇,等.微电网研究综述[J].电力系统自动化,2007,31(19):100-107.

LU Zongxiang, WANG Caixia, MIN Yong, et al. Overview on microgrid research[J]. Automation of Electric Power Systems, 2007, 31(19): 100-107.

[4] CHEN L, MEI S. An integrated control and protection system for photovoltaic microgrids[J]. CSEE Journal of Power and Energy Systems, 2015, 1(1): 36-42.

[5] MEEGAHAPOLA L G, ROBINSON D, AGALGAONKAR A P, et al. Microgrids of commercial buildings: strategies to manage mode transfer from grid connected to islanded mode[J]. IEEE Transactions on Sustainable Energy, 2014, 5(4): 1337-1347.

[6] WANG Y, REN B, ZHONG Q C. Robust power flow control of grid-connected inverters[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 6887-6897.

[7] 时珊珊,鲁宗相,闵勇,等.微电网孤网运行时的频率特性分析[J].电力系统自动化,2011,35(9):36-41.

SHI Shanshan, LU Zongxiang, MIN Yong, et al. Analysis on frequency characteristics of island microgrid[J]. Automation of Electric Power Systems, 2011, 35(9): 36-41.

[8] OUREILIDIS K O, BAKIRTZIS E A, DEMOULIAS C S. Frequency-based control of islanded microgrid with renewable energy sources and energy storage[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(1): 54-62.

[9] de BRABANDERE K, BOLSENS B, van den KEYBUS J, et al. A voltage and frequency droop control method for parallel inverters[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1107-1115.

[10] 郑永伟,陈民铀,李闯,等.自适应调节下垂系数的微电网控制策略[J].电力系统自动化,2013,37(7):6-11.

ZHENG Yongwei, CHEN Minzhou, LI Chuang, et al. A microgrid control strategy based on adaptive drooping coefficient adjusting[J]. Automation of Electric Power Systems, 2013, 37(7): 6-11.

[11] 陈任峰.光伏微网大规模应用关键技术研究[D].北京:清华大学,2013.

[12] ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.

[13] 郑天文,陈来军,陈天一,等.虚拟同步发电机技术及展望[J].电力系统自动化,2015,39(21):165-175.DOI:10.7500/AEPS20150598006.

ZHENG Tianwen, CHEN Laijun, CHEN Tianyi, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175. DOI: 10.7500/AEPS20150598006.

[14] BECK H P, HESSE R. Virtual synchronous machine[C]// 2007 9th International Conference on Electrical Power Quality and Utilisation, October 9-11, 2007, Barcelona, Spain: 1-6.

[15] GAO F, IRAVANI M R. A control strategy for a distributed generation unit in grid-connected and autonomous modes of operation[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 850-859.

[16] 石荣亮,张兴,徐海珍,等.基于虚拟同步发电机的多能互补孤立型微网运行控制策略[J].电力系统自动化,2016,40(18):32-40.DOI:10.7500/AEPS20151015005.

SHI Rongliang, ZHANG Xing, XU Haizhen, et al. Operation control strategy for multi-energy complementary isolated microgrid based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2016, 40(18): 32-40. DOI: 10.7500/AEPS20151015005.

[17] 杨向真,苏建徽,丁明,等.微电网孤岛运行时的频率控制策略[J].电网技术,2010,34(1):164-168.

YANG Xiangzhen, SU Jianhui, DING Ming, et al. Research on frequency control for microgrid in islanded operation[J]. Power System Technology, 2010, 34 (1): 164-168.

[18] 孟建辉,石新春,王毅,等.改善微电网频率稳定性的分布式逆变电源控制策略[J].电工技术学报,2015,30(4):70-79.

MENG Jianhui, SHI Xinchun, WANG Yi, et al. Control strategy of DER inverter for improving frequency stability of microgrid[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 70-79.

[19] LOPES L A C. Self-tuning virtual synchronous machine: a control strategy for energy storage systems to support dynamic frequency control[J]. IEEE Transactions on Energy Conversion, 2014, 29(4): 833-840.

[20] 石荣亮,张兴,刘芳,等.提高光储柴独立微网频率稳定性的虚拟同步发电机控制策略[J].电力系统自动化,2016,40(22):77-85.DOI:10.7500/AEPS20160322016.

SHI Rongliang, ZHANG Xing, LIU Fang, et al. Control strategy of virtual synchronous generator for improving frequency stability of island photovoltaic-battery-diesel microgrid[J]. Automation of Electric Power Systems, 2016, 40(22): 77-85. DOI: 10.7500/AEPS20160322016.

[21] 陈虹.模型预测控制[M].北京:科学出版社,2013.

[22] CORTÉS P, KOURO S, LA ROCCA B, et al. Guidelines for weighting factors design in model predictive control of power converters and drives[C]// IEEE International Conference on Industrial Technology, February 10-13, 2009, Gippsland, VIC, Australia: 1-7.

[23] 梁营玉,张涛,刘建政,等.向无源网络供电的VSC-HVDC模型预测控制[J].电工技术学报,2015,30(11):78-89.

LIANG Yingyu, ZHANG Tao, LIU Jianzheng, et al. Model predictive control for VSC-HVDC supplying passive networks[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 78-89.

[24] 郑泽东,王奎,李永东,等.采用模型预测控制的交流电机电流控制器[J].电工技术学报,2013,28(11):118-123.

ZHENG Zedong, WANG Kui, LI Yongdong, et al. Current controller for AC motors using model predictive control[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 118-123.

[25] 李涵,王毅,张丽荣,等.孤岛模式下的微电网频率的协调控制研究[J].电力科学与工程,2012,28(12):56-62.

LI Han, WANG Yi, ZHANG Lirong, et al. Frequency coordination control strategy for microgrid in island operation[J]. Electric Power Science and Engineering, 2012, 28(12): 56-62.

[26] 焦阳,宋强,刘文华.光伏电池实用仿真模型及光伏发电系统仿真[J].电网技术,2010,34(11):198-202.

JIAO Yang, SONG Qiang, LIU Wenhua. Practical simulation model of photovoltaic cells in photovoltaic generation system and simulation[J]. Power System Technology, 2010, 34(11): 198-202.

[27] SHI H, ZHUO F, YI H, et al. A novel real-time voltage and frequency compensation strategy for photovoltaic-based microgrid[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3545-3556.

陈来军(1984—),男,副教授,主要研究方向:新能源发电与储能技术。

王 任(1992—),男,硕士研究生,主要研究方向:新能源发电与并网。

郑天文(1987—),男,通信作者,博士,主要研究方向:新能源发电运行控制。E-mail: tianwenscu@163.com