面向分布式光伏虚拟集群的有源配电网多级调控

窦晓波, 常莉敏, 倪春花, 段向梅, 葛浦东, 吴在军

(东南大学电气工程学院, 江苏省南京市 210096)

0 引言

分布式光伏(PV)出力具有较强的间歇性、波动性和不确定性,其分散、高渗透接入配电网将导致严重的电压波动、电压越限等问题,影响电网经济安全运行[1-3]。

针对以上问题,目前研究方向主要集中在分布式光伏本地控制与基于全面量测的全局优化两个方面。本地控制主要利用逆变器功率调节能力进行短时间尺度调节。文献[4]将无功检测和补偿控制与光伏并网发电控制相结合,实现并网发电与无功补偿的统一控制;文献[5]提出了光伏有功/无功功率综合控制方案,通过实时设定光伏有功功率并利用逆变器吸收剩余无功功率,从而限制节点电压水平;文献[6]提出了自适应性有功控制策略,限制光伏有功出力以抑制过电压;文献[7]提出基于并网点电压的有功调节与无功调节控制策略;文献[8]提出一种分散式无功就地控制,根据无功功率与电压幅值关系确定光伏无功出力。但单个分布式光伏的调节能力受功率因数、容量等条件限制,仅根据并网点运行状态对其出力进行调节难以实现较大范围的电压调节效果。全局优化则综合考虑配电网全局调控需求,协调各可调控资源进行长时间尺度调度。文献[9]针对有源配电网运行特点,建立综合调度分布式光伏和无功补偿设备的全局优化模型,对过电压进行有效的预防控制。文献[10]针对含高渗透分布式光伏的配电网,提出基于模型预测控制的配电网电压集中控制策略。文献[11-13]以全天有功损耗最小或设备动作次数最小为目标,建立包含如有载调压变压器(OLTC)、电容器(CB)、静止无功补偿器(SVC)等设备与分布式光伏的混合整数动态优化模型;但随着分布式光伏接入点增多,全局优化需协调的调节设备分布广、数目多且存在广域通信延时,导致调控维数高、优化求解过程复杂、响应速度慢,优化结果与配电网实际运行状况偏差大。

为弥补全局优化和本地控制在调控时间尺度、空间范围上的差异性空缺,达到兼顾调节实时性和网络复杂度的效果,本文提出面向分布式光伏虚拟集群的有源配电网多级调控。根据区域配电网多样化的调控目标,基于社团理论动态划分分布式光伏虚拟集群,并对其进行可控能力等值建模;然后,通过研究计及分布式光伏无功调节特性的双时间尺度全局优化调度、基于二次规划的集群趋优控制、含动态修正环节的本地消纳控制,实现对分布式光伏的灵活高效控制;最后,在某实际含高渗透分布式光伏中压配电网改造的38节点网络拓扑上进行仿真,通过算例及仿真分析验证了所提调控方法的正确性和有效性。

1 有源配电网多级调控框架

本节首先提出虚拟集群的概念及其形成。接着,针对有源配电网高维数—多尺度的调控特点,提出面向分布式光伏虚拟集群的多级调控框架,在全局优化调度和本地消纳控制之间增加集群趋优控制环节,明确虚拟集群参与多级调控的过程。

1.1 虚拟集群

虚拟集群以电气距离接近、调控能力相似、控制运行方式一致、利于集中管理等为原则,对分布式光伏进行一体化整合,实现分布式光伏多机统一调度。区别于内部成员固定不变的物理集群,虚拟集群的成员是动态变化的,具有灵活性,能够有效适应配电网调控元素复杂多样、网架结构灵活可变的特点。

虚拟集群的形成主要包括以下几个阶段。

1)系统静态分区。为降低配电网调控的复杂性,采取规则式的方法,以就地消纳、避免无功大范围转移为原则,根据地理属性或行政管理范围,并考虑变电设备位置将配电网划分为多个区域,实现空间解耦。

2)主导节点选取。主导节点需具有可观性和可控性。在一个区域内,以消除某节点电压偏差使区域内其余各节点的电压偏差期望最小为原则[14],选取能反映区域电压水平的节点为主导节点,通过对其进行电压监控,实现对区域节点的监控。

主导节点选择的目标函数为:

(1)

式中:ΔVL为负荷节点电压偏差;κx为衡量负荷相对重要性的变量,其值越大表明负荷重要程度越高。

将含分布式光伏的配电网进行线性化可表示为:

(2)

式中:SLL,SLG,SGL,SGG为灵敏度矩阵;ΔXL为负荷节点扰动量;ΔYG为分布式光伏节点控制量;ΔVG为分布式光伏节点电压偏差。

由式(2)推导得到ΔXL,ΔYG和ΔVL的关系为:

ΔVL=SLLΔXL+SLGΔYG

(3)

从区域中选取P个主导节点,主导节点电压变化ΔVP可以表示为:

ΔVP=CΔVL=MΔXL+BΔYG

(4)

式中:C为0-1矩阵,当节点j为第i个主导节点时,其元素Cij为1,否则为0;M=CSLL;B=CSLG。

利用ΔYG消除主导节点的电压偏差,式(4)可变换为:

ΔVP=MΔXL+BΔYG=0

(5)

为保证调节设备的无功储备,式(5)以控制变量ΔYG最小为目标。

3)虚拟集群分类与划分。针对一个区域内的分布式光伏,根据配电网不同调控目标:经济优化与电压安全,分别划分经济调控集群与紧急调控集群。依据灵敏度信息(相对于主导节点),将电气距离接近、调控能力相似、控制方式相同的分布式光伏划分为满足调控目标的虚拟集群,用于解决区域主导节点电压波动或越限问题。集群对外等值为统一的特性,实现多个集群间协同;集群内具有相应的控制策略,实现群内分布式光伏的协调控制。

1.2 多级调控框架

面向分布式光伏虚拟集群的多级调控框架如图1所示。全局优化调度级以区域经济运行为目标,面向区域内传统无功调节设备(如OLTC,CB,SVC等)和分布式光伏,进行长时间尺度区域经济调度。集群调控主站以T为调度周期,基于最优潮流定时触发全局优化,并划分分布式光伏虚拟集群。考虑到OLTC,CB,SVC以及分布式光伏的不同调节特性,设计全局优化调度模型,为集群趋优控制提供节点电压最优参考值与灵敏度信息。

集群趋优控制级以兼顾区域经济性与安全性为目标,面向区域内分布式光伏虚拟集群,解决调度周期内主导节点电压波动及越限问题。在调度周期T内,采用事件触发方式,集群调控主站根据主导节点电压实时值VP,RT运行区域明确配电网调控目标,进而构造集群趋优目标函数,设计集群趋优控制模型,实现集群间协同优化;集群优化指令快速分配给群内分布式光伏执行,实现对趋优目标的快速协调响应。

本地消纳控制级以保证分布式光伏并网点电压在合格范围内为目标,面向区域内分布式光伏,解决调度周期内并网点电压越限事件。采用事件触发方式,考虑控制过程的动态特性,利用逆变器的功率调节能力,建立含动态修正环节的本地消纳控制模型。

在每个调度周期T内,当负荷波动、分布式光伏出力变化等引起并网点电压越限时,本地控制器优先动作,在较短时间内快速调节并网点电压;之后,集群调控主站根据主导节点电压运行区域,选取合适的虚拟集群类型,基于虚拟集群划分结果协调多个集群进行趋优控制,进一步改善区域电压水平。

主导节点电压运行区域判定如图2所示。对节点电压最优参考值进行适当松弛形成电压优质区,认为配电网的运行同时满足安全性和经济性要求;电压优质区限值与Umax和Umin之间形成电压警戒区,其中Umax和Umin分别为电力系统安全运行规定的上下限值。高于Umax或低于Umin则认为主导节点电压运行在电压不合格区。

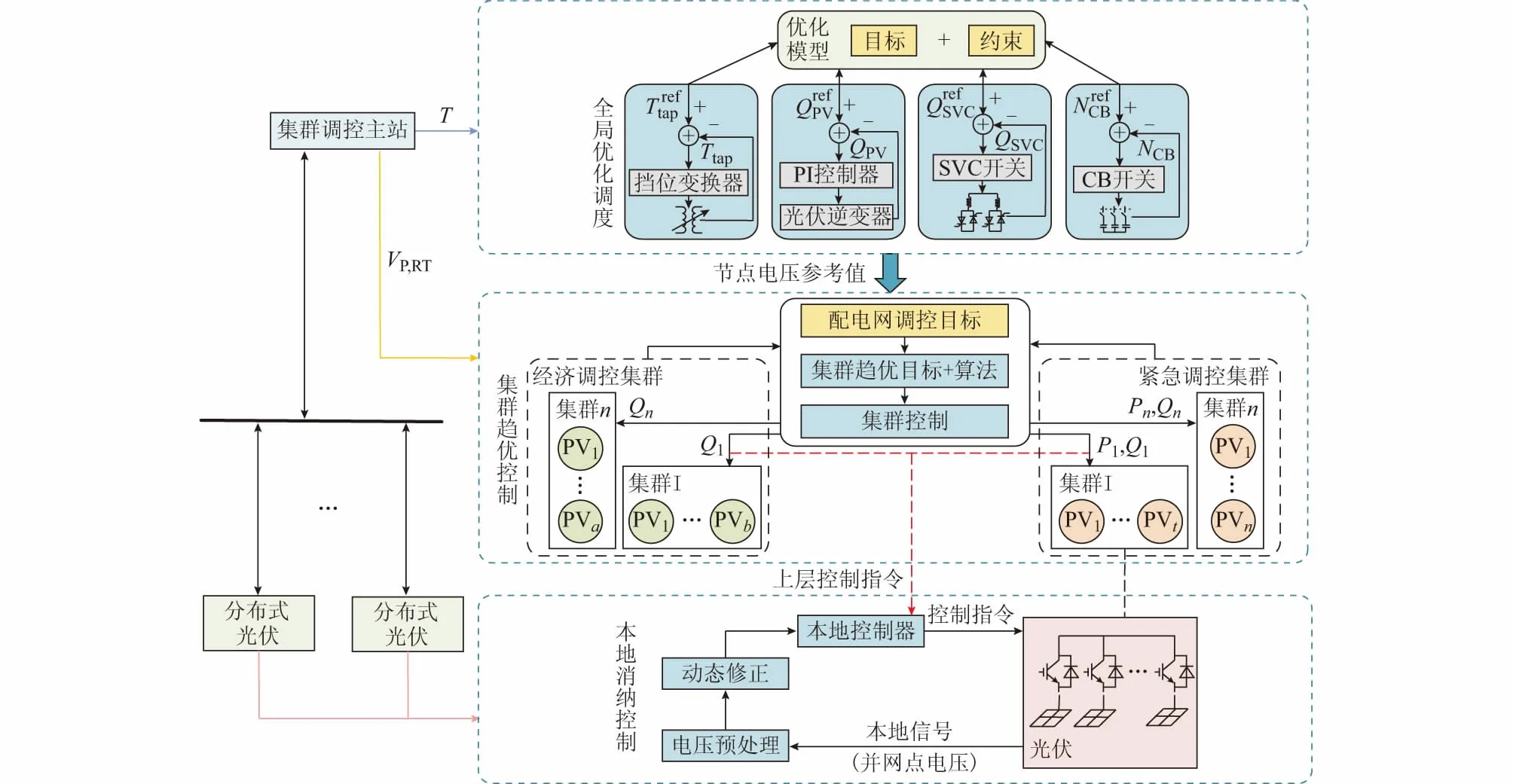
图1 配电网多级调控框架Fig.1 Framework of multi-level dispatching and control in distribution network

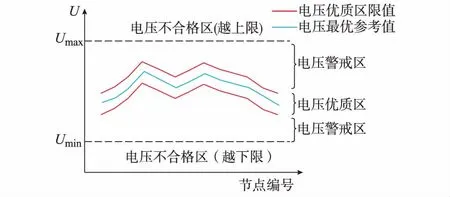
图2 节点运行电压区域判定示意图Fig.2 Schematic diagram of judgment for operation voltage region of node

2 适应调控目标变化的虚拟集群动态划分

本节综合分析分布式光伏调控特性,建立完整的虚拟集群划分指标体系,并根据调控目标选取相应集群的划分指标,据此计算相似度矩阵,建立分布式光伏网络,基于社团理论划分虚拟集群。最后,针对集群参与调控所关注的稳态特性进行可控能力等值建模。

2.1 虚拟集群的划分指标体系

划分分布式光伏虚拟集群需综合考虑分布式光伏的空间分布、调控能力、响应特性、运行方式等特性,主要考虑以下几类划分指标x。

1)有功电压灵敏度JP和无功电压灵敏度JQ

利用灵敏度值反映主导节点电压对不同接入位置的分布式光伏注入功率的响应特性。根据文献[9],基于牛顿—拉夫逊法潮流计算的修正方程并做相应的近似简化,得到主导节点电压变化ΔVP与节点注入功率的线性关系如式(6)所示、有功电压灵敏度JP如式(7)所示、无功电压灵敏度JQ如式(8)所示。

ΔVP=[(B+Q)(G-P)-1(B-Q)+

(G+P)]-1ΔP-[(G-P)(B+Q)-1·

(G+P)+(B-Q)]-1ΔQ

(6)

JP=[(B+Q)(G-P)-1(B-Q)+(G+P)]-1

(7)

JQ=-[(G-P)(B+Q)-1(G+P)+(B-Q)]-1

(8)

式中:B和G分别为节点导纳矩阵的实部和虚部;P和Q分别为节点注入的有功和无功功率矩阵。

2)有功调节容量Pa和无功调节容量Qa

利用调节容量反映分布式光伏的调节能力,对划入集群的分布式光伏进行筛选。分布式光伏的有功、无功出力调节范围分别为:

(9)

(10)

式中:PMPPT为最大功率点跟踪(MPPT)控制方式下分布式光伏有功出力;PRT为分布式光伏有功出力实时值;φmax为最大功率因数角;S为分布式光伏视在功率;Qmax为无功调节容量上限。

3)调节成本L

分布式光伏调节成本包括无功服务补偿成本LQ及有功弃光成本LP,计算公式分别为:

(11)

L=LP+LQ

(12)

式中:Fpv为光伏上网价格;ΔPloss,pv为调节无功增加的损耗;ΔPquit,pv为光伏弃电量。

4)控制方式R、通信方式Y

为降低配电网调控的复杂度,认为集群内各分布式光伏具有相同的控制方式和通信方式。

根据配电网调控目标的不同,对应选取不同类型虚拟集群的划分指标。经济调控集群主要关注调节的经济成本,因此选择JQ,Qa,L,R,Y为划分指标;紧急调控集群则主要关注调节的响应速度,则选择JP,JQ,Pa,Qa,R,Y为划分指标。各划分指标的权重反映其对集群控制的重要程度,对集群划分结果起关键作用。权重的确定需综合考虑调控目标与实际情况,利用主观赋权和客观赋权相结合的方法合理确定。

2.2 虚拟集群的动态划分方法

集群内分布式光伏调控特性相近,集群间分布式光伏调控特性相差较大,与社团结构的特点相似,根据文献[15],利用社团理论可实现分布式光伏集群划分。首先对划分指标进行归一化处理并确定权重,然后计算分布式光伏的相似度矩阵,最后通过优化社团网络评价指标Q值函数实现集群划分。划分流程如附录A图A1所示。

1)划分指标的归一化处理

划分指标x具有不同的量纲,对各个指标作适当的处理使其归一化,压缩到[0,1]中,变换公式为:

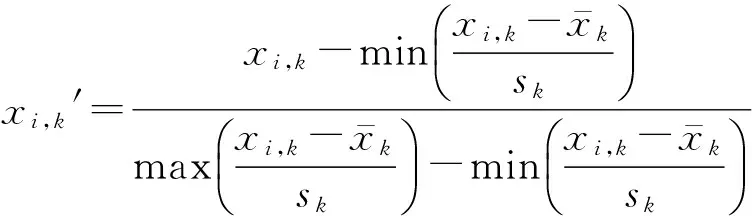
(13)

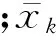
2)相似度矩阵的计算

相似度矩阵中数值越接近1,表示两个分布式光伏特性越相似。本文采用数量积法,计算公式为:

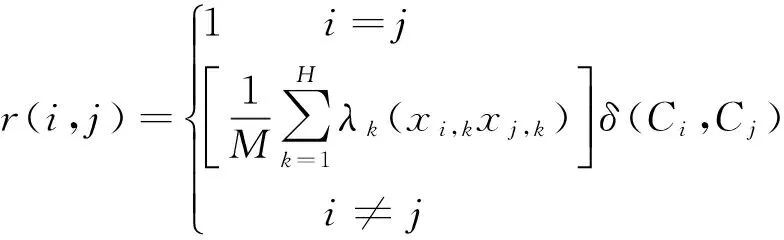
(14)

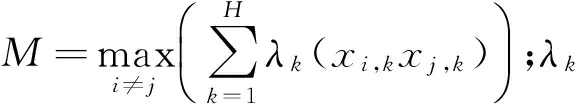
3)优化Q值函数

将单个分布式光伏视为节点,各个节点之间具有连边,连边的权值为分布式光伏的相似度,从而构造分布式光伏网络。Q值函数是社团结构的评价指标,Q值越接近1,表明社团结构越明显[15]。采用层次聚类算法实现Q值函数的优化,即初始以各个节点单独为一个集群,每次按照Q值函数增大的方向进行合并得到新的集群,直至Q值最大,最终得到满足Q值函数最优的分布式光伏虚拟集群划分结果。

分布式光伏网络为加权网络,对Q值函数进行推广,计算公式为:

(15)

式中:gij为网络的连边;ai和aj分别为在节点i,j上连边的权值和;a为网络中所有连边的权值和;Gi为节点i所在集群,当Gi=Gj时,δ=1,否则为0。

2.3 集群可控能力模型

集群可控能力的差异主要体现在灵敏度、功率调节容量、通信方式以及调节成本等方面,因此单个集群等值矩阵E可以表示为:

(16)

忽略各分布式光伏灵敏度的相互影响,节点电压变化采用线性叠加,则集群灵敏度等值公式为:

(17)

(18)

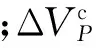
集群功率可调容量与群内各分布式光伏调节能力采用“最大限值和”的形式确定:

(19)

3)集群调节成本Lc

集群调节成本等值主要用于判断集群与其他调节设备之间的成本差异,故在本文中认为不同集群的各分布式光伏调节成本一致。

4)集群控制方式Rc和通信方式Yc

利用不同状态标志表示不同的控制、通信方式。

3 计及分布式光伏无功调节特性的双时间尺度全局优化调度

考虑不削减分布式光伏有功出力以保障用户利益为原则,并计及配电网对离散型无功调节设备(OLTC和CB)的动作次数限制,进行日前动态无功优化。此外,因分布式光伏出力具有波动性,仅依靠日前调度无法对环境等因素做出及时响应,故基于最优潮流及二阶锥规划,计及分布式光伏无功调节特性,设计了一种包含日前计划和日内短期调度的全局优化调度模型。

3.1 双时间尺度调度模型

全局优化调度模型见附录A图A2。

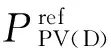
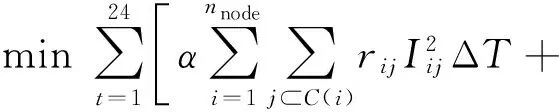
(20)

式中:nnode为网络节点数;j⊂C(i)表示与节点i相连节点构成的集合;rij为支路i-j的阻抗值;Iij为支路i-j的电流幅值;ΔT为调度周期时长;nOLTC和nCB分别为OLTC和CB个数;α,β,γ为各目标权重系数。

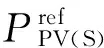
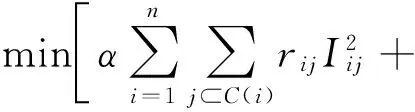
(21)

3.2 数学模型

1)分布式光伏无功调节模型

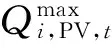
(22)

2)计及分布式光伏无功调节特性的离散设备模型

OLTC以挡位进行调节,其模型可表述为:

(23)

式中:Ti,tap,max和Ti,tap,min分别为第i个OLTC挡位上下限;Ki,t为t时刻OLTC变比;K0和ΔKi分别为标准变比和调节步长;Tmax为一个调度周期内OLTC动作次数限值;Ti,k为相邻调度时刻OLTC调节挡位限值。

CB则以组的形式进行投切,其模型可表述为:

(24)

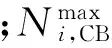
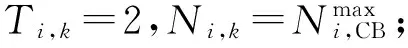
(25)

式中:nPV为分布式光伏个数;ρ为常数。

3)支路潮流模型

根据文献[12],支路潮流模型可表示为:

(26)

式中:Pij和Qij分别为支路i-j的有功和无功功率;Pj,PV和Qj,PV分别为节点j所接分布式光伏注入的有功、无功功率;Pj,d和Qj,d为节点j所接负荷;Qj,CB和Qj,SVC分别为节点j所接CB和SVC注入的无功功率。当支路不含OLTC时,Ki,t=1。

4)关口功率、节点电压、SVC约束见文献[9]。

4 基于二次规划的集群趋优控制

根据区域主导节点电压运行区域,明确配电网调控目标,研究集群趋优控制策略。基于二次规划,考虑集群趋优控制目标的差异性,提出基于无功优化的经济调控集群控制,提升配电网运行经济性;提出基于有功无功协调优化的紧急调控集群控制,快速响应区域内主导节点电压越限事件,保障配电网运行安全。

4.1 集群趋优控制模型

集群趋优控制模型见附录A图A4。

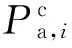
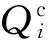
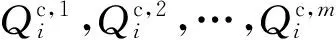
4.2 数学模型

1)集群模型

经济调控集群以主导节点电压偏差最小、集群无功出力变化最小为目标,目标函数如式(27)所示,其物理意义为:①最小化主导节点电压偏差,它隐含尽可能使区域内各节点电压靠近最优参考值的目标;②尽量避免分布式光伏集群出力的反复剧烈变化,它隐含分配调控任务时需考虑各集群的实际状态、尽可能提升调控效率与延长光伏逆变器寿命的目标。

F1=αω1+βω2=

(27)

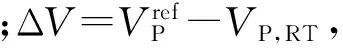
紧急调控集群以主导节点电压偏差最小、集群有功出力削减最小、集群无功出力变化最小为目标,目标函数如式(28)所示,其物理意义为:①以电压安全为首要目标,通过有功无功协调在较短时间内消除电压越限事件;②在保证电压安全前提下,尽可能少削减分布式光伏的有功出力,提高分布式光伏利用率。

F2=αω3+βω4+γω5=

(28)

式中:nem为紧急调控集群个数。

同时,根据集群灵敏度与集群出力的关系,式(27)和式(28)中的ω1和ω3表达式可转换为:

(29)

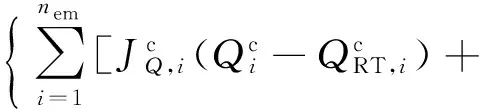
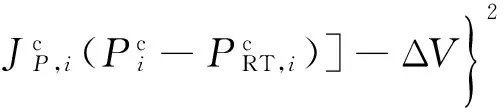
(30)

此外,集群模型应满足功率约束,即

(31)

2)群内功率分配模型

集群内进行功率分配时,各个分布式光伏之间存在参数的差异,如功率上限、实时功率状态以及有功/无功电压灵敏度(相对于主导节点)。由于集群划分时已计及灵敏度的相似性,故主要考虑功率上限和实时功率状态,即分布式光伏的调节裕度。此外,集群模型中以集群出力变化量最小为目标,则在群内功率分配时也需考虑此因素,即分布式光伏的调节效率。因此,依照分布式光伏实时出力比例进行群内功率指令分配。则集群有功功率分配指令可以表示为:

(32)

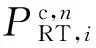
各分布式光伏进行无功调节时,能够吸收或发出容性无功功率,可将实时无功功率值和无功功率上限值同时平移功率上限值进行比例分配。即

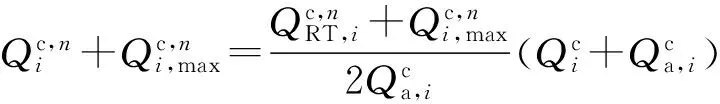
(33)

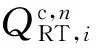
5 含动态修正环节的本地消纳控制

为确保分布式光伏并网点电压在安全范围内,并尽可能提高分布式光伏消纳能力,基于比例—积分(PI)控制,提出充分利用光伏无功能力的本地消纳控制方法。此外,为提高控制过程的动态性能,计及逆变器对功率指令跟踪的时滞性,设计含动态修正环节的本地消纳控制模型,进一步降低分布式光伏并网点电压越限的可能。

5.1 本地消纳控制框架

本地消纳控制主要包括如下3个环节。

1)闭环跟踪控制:以全局优化得到的灵敏度为基础,通过分布式光伏内各并网逆变器的功率跟踪,准确控制分布式光伏并网点电压Vpcc,减少灵敏度误差以及闭环控制过程中产生的误差。同时,分布式光伏可接受全局优化调度和集群趋优控制的控制指令。

2)电压预补偿:基于二次指数平滑法,对分布式光伏出力波动带来的电压波动趋势进行预判,利用指数平滑法所需数据量少、短期预测较准确等特点,简单有效地避免控制器对并网点电压控制的时滞性。

3)电压基准动态修正:以并网点电压预补偿为基础,根据电压预补偿值Vpred,动态修正闭环控制的电压基准值,加快闭环控制指令产生的动态过程,快速抑制电压波动的趋势。

5.2 数学模型

1)闭环跟踪控制模型

模型结构如附录A图A5所示。各逆变器出力据其能力按比例分配,即

(34)

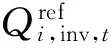
2)电压预补偿

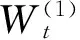
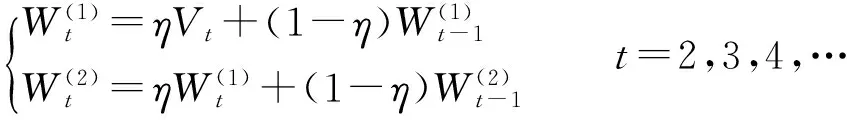
(35)

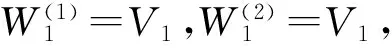
电压预补偿值Vpred取下一个周期预测值,即

(36)

平滑常数η的选取直接影响电压预补偿的精度。需要考虑分布式光伏出力明显且迅速上升或下降的趋势所带来的并网点电压短时波动,宜选择较大的η值,可在0.6至0.8间选值,以使预测模型灵敏度较高。

3)电压基准动态修正

根据分布式光伏并网点Vpred的变化,动态调整闭环控制的电压基准值Vref。当Vpred越限时,通过调整上下限值Vlimited_up和Vlimited_down加快闭环控制功率指令产生的动态过程,尽可能避免分布式光伏并网点电压越限。Vlimited_up和Vlimited_down具体调整如下[16]:

(37)

(38)

式中:μ为比例因子,关系到瞬时电压调整目标。考虑到电压上下限及控制过程可能产生的超调,将电压瞬时调节目标在(Vmax+Vmin)/2的基础上进行缩放,即μ∈(0,0.8(Vmax+Vmin)/2](电压标幺化)。

6 算例分析

6.1 系统参数

基于某地区含分布式光伏的中压配电网实际拓扑,考虑分布式光伏发展趋势对拓扑进行改造,设计如图3所示更典型的含高渗透分布式光伏的配电网结构。详细线路和负荷参数见附录A表A1和表A2。节点1处为OLTC。节点17,19,20,23,27和28处为分布式光伏接入点,光伏接入总容量分别为2.5,2.5,5,1.5,1.5,2.5 MW。默认系统节点电压标幺值上下限为Umin=0.97,Umax=1.07。

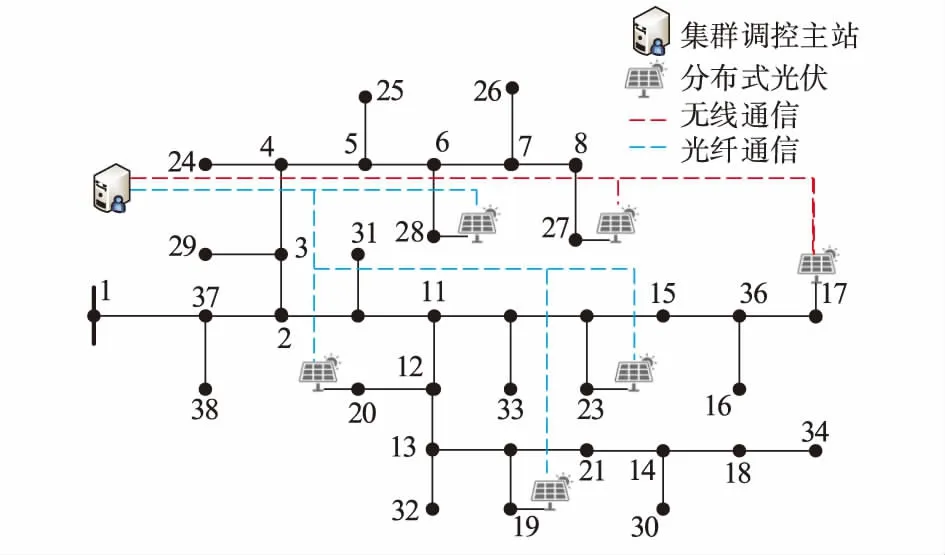
图3 含高渗透分布式光伏的配电网仿真拓扑Fig.3 Simulation topology of distribution network with high-penetration distributed photovoltaic

6.2 结果分析

在分布式光伏高渗透接入配电网的趋势下,过电压是运行控制中较突出的问题。在日间较强光照且较低负荷水平时段,电压越上限问题突出,故选取该具有代表性的极端运行情况进行仿真。

6.2.1集群划分结果

通过对比在不同调控目标下分布式光伏间相似度及集群划分结果的变化,验证配电网运行状态变化时所提划分方法的动态适应性。图3中节点17,27处的分布式光伏与调控主站之间采用无线通信方式,其余节点处的分布式光伏则采用光纤通信方式。经济优化、电压安全调控目标下分布式光伏相似度矩阵的色块分别如附录A图A6(a)和(b)所示。横纵坐标表示分布式光伏接入处的节点编号,不同色块代表不同的相似度值(与色块标尺对应)。分布式光伏间相似度越高,对应值越接近1。相似度矩阵具体计算结果见附录A表A3、表A4。根据相似度矩阵建立分布式光伏网络,优化Q值函数获得如表1所示的集群划分结果。

表1 集群划分结果Table 1 Results of cluster division

6.2.2多级调控结果

模拟天气由阴转晴,各分布式光伏有功出力迅速增大,若此时线路负荷较轻则可能引起线路电压抬升甚至越限。这种情况下,传统配电网通过投入并联电抗器或调整OLTC挡位以调节馈线电压,分布式光伏高渗透分散接入导致各设备协调难度大,可能会出现设备投切振荡。本文所提多级调控方法以虚拟集群的形式协调各分布式光伏参与电压调控,通过全局优化调度、集群趋优控制和本地消纳控制的配合实现高维数—多尺度的区域电压控制。

1)全局优化调度

假设在某调度周期起始时刻,系统节点1处母线电压为1.035(标幺值)(由日前计划确定的OLTC的挡位可知),日内短期调度优化后的分布式光伏出力如附录A表A5所示。全局优化前网络损耗为3.31 kW,优化后的网络损耗为1.02 kW,优化后线路网损降低了69.18%,主导节点20的电压参考值为1.041(标幺值)。各分布式光伏有功出力曲线如附录A图A7所示,日间线路负荷数据见附录A表A2。本文主要研究高渗透分布式光伏有功出力变化对配电网的影响,故算例中未考虑负荷特性变化,采用固定的负荷参数。

2)本地消纳控制

如附录A图A8所示,当采用无动态修正环节的电压闭环控制策略时,t1′时刻主导节点20的电压越上限触发本地消纳控制,t1′+Δt时刻电压越限事件仍未解决,触发紧急调控集群控制,由3个集群协调控制使电压尽快恢复至警戒区;通过增加动态修正环节可有效抑制电压调节过程的超调越限,t1+Δt时刻由于电压越限事件已经解决,并未触发紧急调控集群控制。

3)集群趋优控制

为体现多级调控在保障有源配电网安全经济运行方面的优势,分析不同优化模型在调压效果、调控维数等方面的差异性,对比有功、无功协调优化[9,17](策略1)、分布式光伏并网点电压控制[18](策略2)和本文所提出的多级调控(策略3)等三种调控方法下电网运行状态的变化,如图4所示。

主导节点电压变化如图4(a)所示,t1时刻主导 节点20电压快速上升接近运行上限。采用策略1时,基于全局量测量进行有功、无功协调优化,经过一定延迟,t4时刻开始动作,并于t5时刻主导节点恢复稳定运行。采用策略2时,于t1时刻进行控制,并于t2时刻左右主导节点恢复安全运行。采用策略3时,立即触发分布式光伏本地消纳控制(含动态修正环节),利用其无功调节容量进行闭环调节,由于设计了含动态修正环节的本地消纳控制,本地控制层快速动作,有效避免t2时刻电压越限事件触发紧急调控集群控制,t3时刻主导节点电压运行在警戒区,触发3个经济调控集群协调实现经济优化,使主导节点电压接近优质区。

由图4(a)可直观地看到:策略2虽动作较快,但单个并网点调节能力有限,调压效果较差;策略1和策略3均可达到显著的调压效果,但策略1动作延迟较长。选取图4(a)中所示t5时刻,区域内各节点在策略1、策略2、策略3作用下的整体电压分布如图4(b)所示。可以看出,策略2作用下的区域各节点电压与最优参考值间存在较大偏差,策略3则能保证区域各节点电压非常接近最优参考值。

各调控方法下的网络损耗、节点平均电压偏差、计算时间、调控维数以及分布式光伏有功削减与无功出力等具体如表2所示。

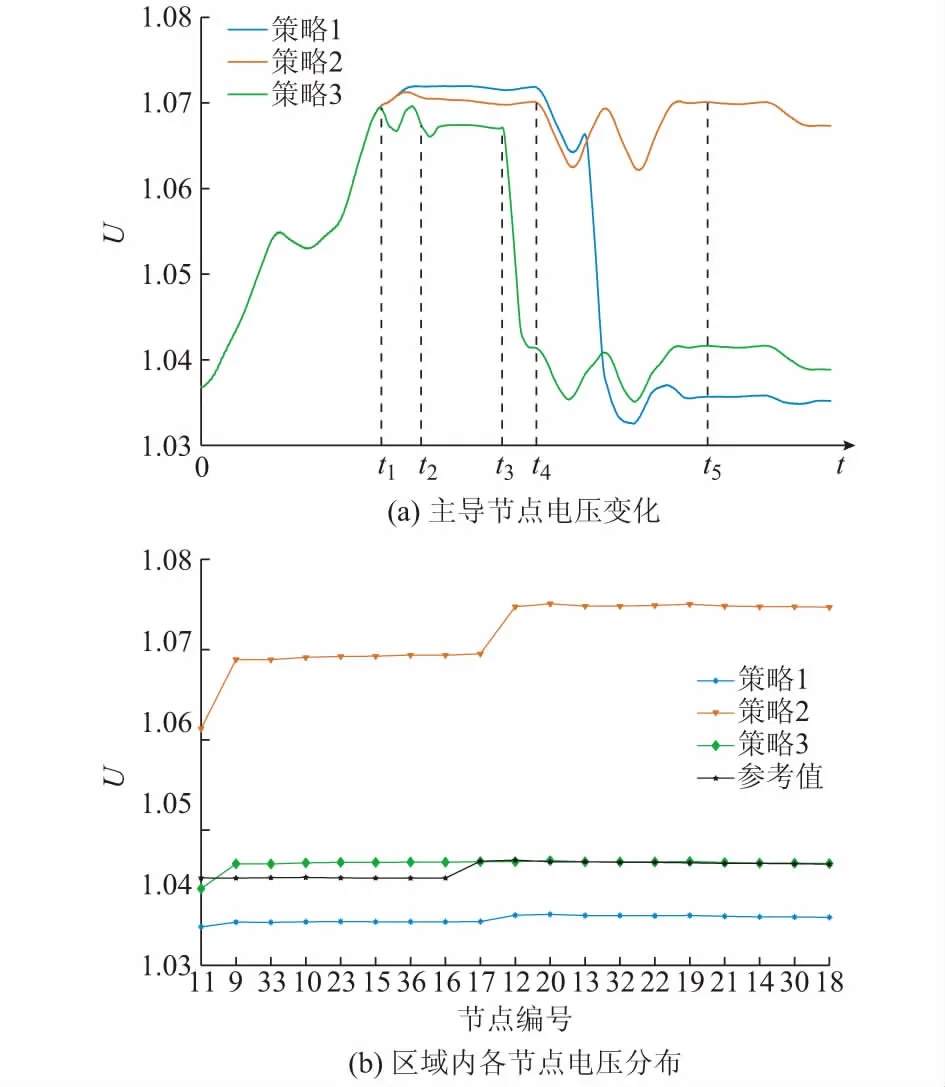
图4 不同调控策略节点电压状态Fig.4 Node voltage states under different control strategies

由表2数据分析可知:①调压效果方面,策略3作用下节点平均电压偏差最小,相较于策略1和策略2分别减少48.78%和86.71%;②调控维数方面,策略2调控维数最小,策略3相较于策略1减少75%;③计算时间方面,策略1计算时间最长,策略3相较于策略1减少92.2%;④经济性方面,策略1作用下节点19,20分布式光伏削减一定有功功率,策略3作用下网络损耗有所增加。这说明,由于多级调控主要通过调节分布式光伏无功出力来快速调整运行电压,故可能会引起系统网络损耗的增加,但其对消除电压偏差起到更积极的影响。

因此,本文所提多级调控策略3相对于策略1在调控维数、计算时间方面具有较大优势,相对于策略2具有更显著的调压效果,能够实现调控的快速性与有效性,保障有源配电网运行安全经济。

7 结语

本文提出虚拟集群概念,并基于社团理论提出适应调控目标变化的虚拟集群动态划分方法。基于此,研究了包含全局优化调度、集群趋优控制、本地消纳控制的有源配电网多级调控,为含高渗透分布式光伏配电网的调度控制难题提供了一种有效的解决方法。然而,本文工作在功率电压灵敏度获取、通信等方面存在一定局限性,今后将研究功率电压灵敏度修正方法,及应对复杂通信状况的有源配电网集群调控方法。

本文受到智能电网保护和运行控制国家重点实验室资助,特此感谢。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 尤毅,刘东,于文鹏,等.主动配电网技术及其进展[J].电力系统自动化,2012,36(18):10-16.

YOU Yi, LIU Dong, YU Wenpeng, et al. Technology and its trends of active distribution network[J]. Automation of Electric Power Systems, 2012, 36(18): 10-16.

[2] WALLING R A, SAINT R, DUGAN R C, et al. Summary of distributed resources impact on power delivery systems[J]. IEEE Transactions on Power Delivery, 2008, 23(3): 1636-1644.

[3] SCHONARDIE M F, MARTINS D C. Application of thedq0 transformation in the three-phase grid-connected PV systems with active and reactive control[C]// 2008 IEEE International Conference on Sustainable Energy Technologies, November 24-27, 2008, Singapore: 18-23.

[4] 汪海宁,苏建徽,张国荣,等.光伏并网发电及无功补偿的统一控制[J].电工技术学报,2005,20(9):114-118.

WANG Haining, SU Jianhui, ZHANG Guorong, et al. Unitive control of PV grid connected generation and reactive compensation[J]. Transactions of China Electrotechnical Society, 2005, 20(9): 114-118.

[5] 李清然,张建成.含分布式光伏电源的配电网电压越限解决方案[J].电力系统自动化,2015,39(22):117-123.DOI:10.7500/AEPS20150125001.

LI Qingran, ZHANG Jiancheng. Solutions of voltage beyond limits in distribution network with distributed photovoltaic generators[J]. Automation of Electric Power Systems, 2015, 39(22): 117-123. DOI: 10.7500/AEPS20150125001.

[6] ALYAMI S, WANG Y, WANG C, et al. Adaptive real power capping method for fair overvoltage regulation of distribution networks with high penetration of PV systems[J]. IEEE Transactions on Smart Grid, 2014, 5(6): 2729-2738.

[7] 魏昊焜,刘健,高慧.分布式电源的本地电压控制策略[J].电力自动化设备,2016,36(9):40-45.

WEI Haokun, LIU Jian, GAO Hui. Local voltage control of distributed generations[J]. Automation Electric Power of Automation Equipment, 2016, 36(9): 40-45.

[8] MOLING G A, MASTROMAURO R A, LISERRE M. A combined centralized/decentralized voltage regulation method for PV inverters in LV distribution networks[C]// IEEE PES General Meeting/Conference & Exposition, July 27-31, 2014, National Harbor, MD, USA: 1-5.

[9] 刘一兵,吴文传,张伯明,等.基于有功——无功协调优化的主动配电网过电压预防控制方法[J].电力系统自动化,2014,38(9):184-191.DOI:10.7500/AEPS20131101003.

LIU Yibing, WU Wenchuan, ZHANG Boming, et al. Overvoltage control method based on active and reactive power coordinated optimization in distribution network[J]. Automation of Electric Power Systems, 2014, 38(9): 184-191. DOI: 10.7500/AEPS20131101003.

[10] VALVERDE G, VAN CUTSEM T. Model predictive control of voltages in active distribution networks[J]. IEEE Transactions on Smart Grid, 2013, 4(4): 2152-2161.

[11] DARATHA N, DAS B, SHARMA J. Coordination between OLTC and SVC for voltage regulation in unbalanced distribution system distributed generation[J]. IEEE Transactions on Power Systems, 2014, 29(1): 289-299.

[12] 刘斌,刘锋,梅生伟,等.基于二阶锥优化的含有载调压变压器主动配电网最优潮流[J].电力系统自动化,2015,39(19):40-47.DOI:10.7500/AEPS20150104003.

LIU Bin, LIU Feng, MEI Shengwei, et al. Optimal power flow in active distribution networks with on-load tap changer based on second-order cone programming[J]. Automation of Electric Power Systems, 2015, 39(19): 40-47. DOI: 10.7500/AEPS20150104003.

[13] 刘明波,朱春明,钱康龄,等.计及控制设备动作次数约束的动态无功优化算法[J].中国电机工程学报,2004,24(3):34-40.

LIU Mingbo, ZHU Chunming, QIAN Kangling, et al. Dynamic reactive power optimization algorithm incorporating action number constraints of control devices[J]. Proceedings of the CSEE, 2004, 24(3): 34-40.

[14] 贠志皓,刘玉田,梁军,等.考虑风电功率波动概率特性的主导节点选择方法[J].电力系统自动化,2014,38(9):20-25.DOI:10.7500/AEPS20130326003.

YUN Zhihao, LIU Yutian, LIANG Jun, et al. A pilot node selection method considering probability characteristics of wind power fluctuation[J]. Automation of Electric Power Systems, 2014, 38(9): 20-25. DOI: 10.7500/AEPS20130326003.

[15] 潘高峰,王星华,彭显刚,等.基于社团结构理论的电网无功分区及主导节点选择方法研究[J].电力系统保护与控制,2013,41(22):32-37.

PAN Gaofeng, WANG Xinghua, PENG Xiangang, et al. Improved network partition and pilot node selection method for reactive power/voltage control based on community detection algorithm[J]. Power Systems Protection and Control, 2013, 41(22): 32-37.

[16] ALI M, REZA I. Online set point adjustment for trajectory shaping in microgrid applications[J]. IEEE Transactions on Power Systems, 2012, 27(1): 216-223.

[17] 吴富杰,苏小林,阎晓霞,等.基于多目标的主动配电网有功无功协调优化[J].自动化技术与应用,2015,34(11):59-65.

WU Fujie, SU Xiaolin, YAN Xiaoxia, et al. Multi-objective based optimization on active and reactive power coordinated control in active distribution network[J]. Techniques of Automation & Application, 2015, 34(11): 59-65.

[18] 周林,晁阳,廖波,等.低压网络中并网逆变器调压策略[J].电网技术,2013,37(9):2427-2432.

ZHOU Lin, CHAO Yang, LIAO Bo, et al. A voltage regulation strategy by grid-connected PV inverters in low-voltage networks[J]. Power System Technology, 2013, 37(9): 2427-2432.

窦晓波(1979—),男,通信作者,博士,教授,主要研究方向:分布式电源(储能)变流器优化控制、分布式电源高渗透配电网、分布式发电与微电网。E-mail： dxb_2001@sina.com

常莉敏(1992—),女,硕士研究生,主要研究方向:分布式电源高渗透配电网优化。E-mail: changlimin310@163.com

倪春花(1992—),女,硕士研究生,主要研究方向:分布式电源高渗透配电网。E-mail: nch_seu@163.com