直流配电网下垂参数小干扰稳定优化调控方法

孙峰洲, 马骏超, 朱 洁, 赵 贺, 于 淼, 韦 巍

(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 国网浙江省电力有限公司电力科学研究院, 浙江省杭州市 310014; 3. 国网北京电力科学研究院, 北京市 100075)

0 引言

随着新能源的快速发展,分布式电源(DG)和配电网的耦合问题受到了广泛关注[1]。在此背景下,直流配电网由于具有新能源接入效率高、负荷供电可靠性强、系统调控灵活性好等优势,其应用前景不可小觑[2]。在直流配电网运行调控中,下垂控制是一类较为主流的控制方式,通过多变流器间的下垂协调来提供电压支撑,可以在降低通信需求的同时,减少不确定源荷功率随机波动对系统的影响,从而有效提高系统运行的安全性和经济性[3]。

下垂参数的合理设置对直流配电网的安全经济运行至关重要。针对下垂控制模式下系统的经济运行问题,文献[4]基于发电成本曲线提出了一种直流系统分布式下垂调控策略,在降低系统通信需求的同时,满足负荷用电、降低发电成本。文献[5]对中压直流配电网的变流器下垂参数进行多时间尺度协调优化,有效降低了不确定性源荷预测误差对系统调控过程中经济性和安全性的不利影响。文献[6]针对不确定源荷的功率随机波动问题,提出基于动态下垂控制的联络线定功率控制方法,使功率波动量得到经济合理分配。但上述文献均未详细考虑下垂斜率对系统小干扰稳定的影响,系统在调控指令的作用下能否稳定运行有待进一步理论验证。

针对小干扰稳定问题,文献[7]基于矩阵摄动理论对交流微网中逆变器的下垂参数进行协调优化,从而保障交流微网的小干扰稳定运行。但是该方法仅以系统稳定性作为优化目标,忽略了由下垂控制单元分担系统净功率波动时的经济性。文献[8]基于状态空间模型,提出交流配电网下垂调控策略,在实现系统小干扰稳定运行的同时,一定程度上提高了功率利用效率。但该策略没有考虑下垂控制和系统潮流间的交互作用,忽略了不确定源荷功率随机波动的影响,同时下垂参数的选取也较为保守,没有进行优化,因此系统经济性有待进一步提高。

综上所述,在系统运行优化问题中同时考虑经济性和小干扰稳定性十分必要。文献[9]研究了包含小干扰稳定约束的最优潮流模型,但未考虑变流器动态特性对系统稳定运行的影响。同时采用序列线性规划算法求解优化潮流(OPF)模型,其优化结果和收敛性对初值较敏感,且特征值近似误差在迭代过程中存在不断积累的问题,最终将对优化结果产生较大影响,因而有待改进。文献[10]采用转换模型法将考虑特征值约束的非线性半定规划模型转化为一般非线性规划模型,但该方法会极大地增加优化问题的求解规模,计算效率有待进一步提升。

鉴于以上问题,本文针对含AC/DC和DC/DC变流器的环状直流配电网小信号状态空间模型[11-14],考虑其下垂控制模式,分析了下垂参数对直流配电网小干扰稳定性的影响。基于状态空间模型建立了考虑小干扰稳定约束的直流配电网下垂参数优化调控模型。在该模型中以下垂斜率作为优化变量,将小干扰稳定条件作为问题约束,从而保证系统在预测场景和极端场景下的稳定运行,并使得总运行网损最小。方法创新点如下:①考虑短期预测数据存在误差,提出基于极端场景的小干扰稳定约束,提高系统应对不确定源荷功率随机波动的鲁棒性,以较小的经济代价换取系统安全性的显著提升;②对于优化模型的求解,在序列非线性规划算法和遗传算法的基础上提出相应改进策略,在保证优化结果可靠有效的前提下提高算法的寻优能力和计算效率。最后通过数值实验和仿真对本文所提方法的调控效果进行了验证。

1 直流配电网状态空间模型

以环状拓扑为例,直流配电网典型结构[11]如图1所示。直流配电网中包含了AC/DC和DC/DC两类最为常见的电力电子变流设备。系统通过前者可拓展接入风机、交流负荷与交流可控DG,通过后者可拓展接入光伏、储能和直流负荷。

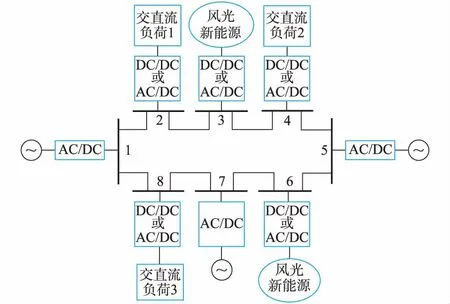
图1 直流配电网结构Fig.1 Configuration of a DC distribution system

1.1 AC/DC变流器小信号模型

AC/DC变流器选用三相电压源型换流器(VSC),采用PV下垂及电压电流双环控制,变流器及其控制结构模型见附录A。

电流环采用dq轴解耦控制。由于本文重点研究直流配电网侧不确定源荷功率随机波动带来的稳定问题,故令交直流功率守恒,交流侧大电网电压无扰动,交流侧无功指令为0,q轴电流无扰动,则小信号模型中只需考虑d轴电流控制环[12]。其微分方程模型参考文献[12-13],具体表达式见附录A。对微分方程在稳态运行点附近线性化,即可得到AC/DC变流器小信号状态空间模型。交流负荷并网AC/DC变流器模型与之类似。

1.2 DC/DC变流器小信号模型

DC/DC变流器整体结构及控制框图见附录B。采用Boost/Buck电路,与直流源荷耦合。以光伏并网Boost电路为例,光伏电池采用经典的工程用模型,单电压环最大功率点跟踪(MPPT)控制[14],通过改变Boost电路的占空比D来控制光伏电池的输出电压等于最大功率点电压um。

光伏发电系统微分方程模型参考文献[14],具体表达式见附录B。对微分方程在稳态运行点附近线性化,即可得到光伏发电系统小信号状态空间模型,直流负荷并网DC/DC变流器模型与之类似。

1.3 直流线路小信号模型

直流配电网线路暂态模型见附录C。其微分方程模型包括节点KCL方程和支路电压方程,具体表达式见附录C。对微分方程在稳态运行点附近线性化,即可得到直流线路小信号状态空间模型。

1.4 直流配电网系统小信号模型

结合具体配电网结构,将各模块的状态空间模型联立,保留状态变量,消去其他无关变量,即可得到直流配电网系统整体的小信号状态空间模型:

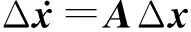
(1)

式中:矩阵A即为系统的状态矩阵,当A的特征值全部在s域左半平面时,直流配电网系统在稳态运行点附近小干扰稳定。稳态点可以通过仿真或解稳态潮流方程获得,本文采用后者计算得到状态矩阵中的稳态运行点参数。

2 考虑小干扰稳定约束的下垂斜率优化模型

变流器下垂控制的调控指令包括下垂参考点和下垂斜率。为协调多个变流器之间的功率输出,提高变流器下垂控制与潮流分布交互影响下的电能利用效率,且保证该过程中系统稳定运行,模型以短期预测数据和下垂参考点作为输入,以下垂斜率作为优化变量。其中,下垂参考点包括电压参考值udcref和功率参考值Pref,可参考文献[5],基于长期预测数据优化得到。

2.1 目标函数

直流配电网功率平衡关系如式(2)所示。

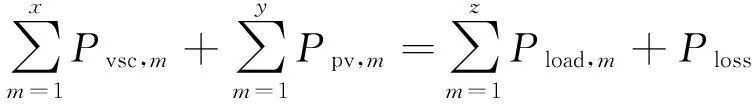
(2)

式中:Pvsc,m为第m台VSC出力;Ppv,m为第m台光伏出力;Pload,m为第m个负荷所需功率;Ploss为考虑网架结构和线路阻抗后的系统网损总和;x,y,z分别为VSC、光伏与负荷的个数。

为提升直流配电网运行经济性,需在满足负荷需求前提下使得系统总网损最小。由式(2)可知,当系统总网损最小时,VSC出力之和最小,故可将VSC出力大小作为直流配电网的网损衡量指标。

定义调控时间窗为指令更新间隔时段,则变流器在调控时间窗的初始时刻接收调控指令,此后根据该指令自动响应不确定性源荷功率的随机波动。基于上述功率平衡关系的分析结果,优化模型以调控时间窗内不同时刻的系统运行总网损累计值最小为优化目标,其目标函数如式(3)所示。

(3)

式中:Pvsc,t,m为调控时间窗内t时刻第m台VSC的出力,是关于下垂斜率k1,k2,…,kx的隐函数;n为调控时间窗内的离散时刻数。

2.2 基于确定性预测场景的约束条件

调控时间窗内的n组确定性短期预测场景均要满足下列约束,以下公式中省略时间下标t。

1)网络潮流功率平衡约束

(4)

式中:Pi,inj为第i个节点的注入功率;un,i和un,j分别为节点i和j的电压;Gdc,ij为网络导纳矩阵中对应节点i和j的元素值;Ndc为网络节点个数。

2)节点电压、支路电流约束

un,min≤un,i≤un,max

(5)

-Il,max≤Il,i≤Il,max

(6)

式中:Il,i为第i条支路的电流,Il,max为其上限;un,max和un,min分别为节点电压的上、下限。电压和电流的上、下限考虑了短期预测数据存在误差时的裕量。

3)VSC容量备用约束

(7)

4)下垂约束

udcref,m-un,i=km(Pvsc,m-Pref,m)

(8)

式中:km为第m个VSC的下垂斜率。

5)小干扰稳定约束

Re(λ)max<ηmax

(9)

式中:ηmax为最大谱横坐标[10],即特征值实部的最大允许值,以衡量系统的稳定裕度;Re(λ)max为状态方程特征值的最大实部。当所有短期预测场景下系统状态方程特征值最大实部满足式(9)时,系统小干扰稳定。

由于状态矩阵的特征值函数无法精确显式解析表示,因此采用矩阵摄动理论对其进行线性化近似[15-16]。当优化变量摄动率足够小时,采用特征值一阶摄动即可得到足够高的精度[7]。对于直流配电网小信号状态空间方程,由于其满足孤立特征值非亏损系统判定条件[15],同时下垂斜率对于稳态运行点的影响在特征值摄动过程中可以忽略[7],故状态矩阵中只有若干元素是下垂斜率的显函数,且均为一次函数,此时矩阵A可以表示为:

A=A0+k1M1+k2M2+…+kxMx

(10)

式中:A0和Mm(m=1,2,…,x)在给定的稳态运行点上为与优化变量无关的定常系数矩阵。

下垂斜率改变时特征值近似解析式为:

λi=λi0+Δk1λi1,1+Δk2λi1,2+…+Δkxλi1,x

(11)

式中:λi0为在某一给定稳态运行点下第i个特征值的初值;Δkm为第m台VSC的下垂斜率改变量,m=1,2,…,x;λi1,m为第i个特征值一阶摄动量的第m个分量,其计算公式为

(12)

vi0和ui0分别为在给定稳态运行点处,λi0对应的正交右特征向量和左特征向量,均为常数向量。

特征值约束式(9)借助式(10)至式(12)得以近似解析表示,则含小干扰稳定约束的优化问题可通过矩阵摄动理论转变为一般非线性优化问题求解。

6)下垂斜率摄动约束。为保证特征值近似计算的精度,需要加入优化变量摄动约束,即

Δkm<αk0,m+ω

(13)

式中:α为单次循环摄动率;k0,m为下垂斜率初值;ω为最小摄动阈值。

2.3 基于极端场景的约束条件

在式(4)至式(13)的约束中,均没有考虑短期预测数据的预测误差。但由于新能源和负荷的发用电功率具有不确定性,实际运行场景与预测场景之间可能存在一定偏差,此时若在小干扰约束中仅考虑确定性场景,则所得优化指令将可能无法保证系统在实际场景下的稳定运行。因此,增加基于极端场景的小干扰稳定约束对上述优化模型进行改进。

通过遍历的方法分析各新能源与负荷节点注入功率变化对系统小干扰稳定性的影响[8]。以图1所示的环状直流配电网接入光伏和直流负荷为例,由蒙特卡洛数值实验可知,该拓扑下直流配电网小干扰稳定性随各节点负荷消耗功率的减少或光伏出力的增加而逐渐下降,分析详见附录D。由此可得,在已知预测数据误差范围的情况下[17],当各负荷功率达到预测范围下限且各光伏出力达到预测范围上限,即系统的净负荷达到预测范围内最小值时,系统稳定性最弱。因此,定义预测范围内净负荷功率达到最小值的场景为极端场景,并通过增加极端场景下的小干扰稳定约束来提高系统应对新能源与负荷功率随机波动的鲁棒性。

在极端场景量化选取方面,每一个确定性预测场景均存在相对应的极端场景,即共有n组极端场景。令某确定性预测场景中第i个负荷预测功率为Pload,i,第i台光伏预测出力为PPV,i,误差率为σ,则该确定性预测场景所对应的极端场景中第i个负荷的功率为Pload,i(1-σ),第i台光伏出力为PPV,i(1+σ)。对极端场景下的稳态运行点进行小信号线性化,增加极端场景下系统小信号状态矩阵的特征值谱横坐标约束。对每个极端场景,如式(4)至式(13)所示约束条件保持不变,同时由于极端场景下的小干扰稳定约束强于确定性预测场景,故确定性预测场景下小干扰稳定约束式(9)至式(12)可省略,以提高优化算法的计算速度。

值得说明的是,系统稳定性和经济性的权衡取决于预测误差率σ,而该参数受预测设备的精度和预测数据的时间尺度等因素影响。σ越大,则极端场景下的小干扰稳定约束越强,系统应对不确定源荷功率随机波动的鲁棒性越强,但网损优化的寻优空间相应缩小,从而导致经济性下降,网损增大。本文参考文献[17],令σ=20%。

3 基于改进策略的求解算法

如前文所述,求解上述模型的方法主要包括基于矩阵摄动理论的序列非线性规划法和遗传算法等智能算法。前者只有一条寻优收敛路径,对初值点敏感,易陷入摄动范围内的局部最优解,且特征值近似误差在迭代过程中可能不断积累,使优化指令的可靠性降低。而后者虽然可以对非凸优化问题进行有效求解,但其本质是寻优空间内多离散点比较寻优的搜索算法,在连续优化空间内准确的最优解几乎无法通过遗传操作得到,同时计算效率较低。

针对下垂斜率优化模型求解,本文在序列非线性规划算法和遗传算法基础上提出如下改进策略。

1)针对基于矩阵摄动理论的序列非线性规划算法单点摄动易陷入局部最优解的问题,采用两层嵌套求解框架,上层采用改进遗传算法[18],下层采用序列非线性规划算法,设计两层优化算法之间的交互协调策略以提高算法效率。其中,下层非线性规划算法采用内点法[10]。将遗传算法和序列非线性规划算法进行嵌套,通过遗传算法对种群每个个体进行特征值摄动迭代,之后再进行比较寻优,能有效跳出局部最优解。同时将传统遗传算法的多离散点比较寻优转变为多子空间局部最优解的比较寻优,可以有效提高算法的寻优能力。

2)针对基于矩阵摄动理论的序列非线性规划算法迭代过程中特征值误差不断积累的问题,在下层内点法向上层遗传算法传递优化结果时增加校验步骤,用QR法[19]求解特征值的准确值,如果由于误差导致实际特征值越限,则在目标函数中添加罚函数项。因此内点法中目标函数保持不变,上层遗传算法目标函数修正为:

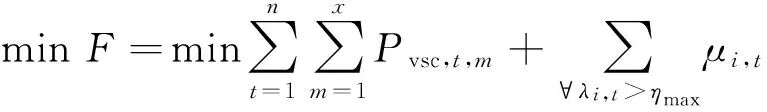
(14)

式中:μi,t为对所有越限特征值设置的惩罚项。

改进策略2)对遗传算法中的目标函数增设罚函数项,用QR法对特征值进行准确校验,能在不显著增加程序运行时间的基础上,有效解决下层算法中特征值近似误差积累的问题。该策略同时能克服部分场景下由于初值不合理而导致优化模型小干扰稳定约束和摄动量约束出现互斥,进而造成内点法不收敛的问题。

3)由于上层引入遗传算法,对每一个个体均要进行完整的序列非线性规划算法收敛过程,随着个体数增加,计算时间成正比增加。摄动率步长和循环迭代次数之间呈近似反对数关系,摄动率的限制会导致循环迭代次数显著增加,从而使计算效率有所降低。

针对上述问题,设计预筛选策略。令下层最大循环次数为Fmax,定义采用内点法进行一次求解,反复迭代至收敛的过程为一个循环,当下层循环次数大于Fmax时,再通过QR法进行特征值校正,否则只采用近似特征值参与循环迭代。下层最大循环次数的设置,其目的在于将种群中每个个体的收敛曲线分层分段实现。每个个体的收敛曲线在下层循环中只完成一段,到达最大循环次数后就返回上层遗传算法进行择优,排除寻优潜力较差的初值点和轨迹,保留收敛性较好的轨迹曲线,再代入下层序列内点法继续寻优过程。

在此基础上,为进一步提高寻优效率,对迭代摄动率采用放缩策略,其流程图见附录D图D2。

令初始摄动率α0为100%,若校验中由于摄动误差导致优化结果实际小干扰不稳定,则在未达到最大校验次数的前提下对摄动率进行紧缩,重新返回下层进行优化。该放缩步骤能显著减少循环迭代次数,进而提高计算效率,同时由于存在特征值校正步骤,不会由于特征值近似误差增加而牺牲算法的寻优准确性。

综上所述,本文所提出的改进策略能在保证优化结果可靠有效的前提下,提高算法的寻优能力和计算效率。

下垂斜率优化算法流程图见附录D图D3。下垂斜率优化程序输入为短期预测数据和下垂参考点,输出为下垂斜率指令。具体步骤说明见附录D。

4 算例分析

算例采用如图1所示的典型环状直流配电网,额定电压等级为800 V[20],功率基值为50 kW,VSC额定容量为100 kW。由于直流配电网中接入分布式直流源和直流负荷时能量利用效率较高,因此算例中以光伏作为城市配电网典型新能源,以直流负荷作为典型负荷。其中,光伏额定容量为50 kW,直流负荷峰值容量为100 kW。直流系统参数见附录D表D1。参考点指令更新周期为5 min,下垂斜率指令更新周期为1 min,1 min内每15 s一组短期预测数据。在该算例下,下垂斜率优化模型参数见附录D表D2。直流配电网状态矩阵具体表达式见附录E。

4.1 下垂参数对直流配电网稳定性的影响

当大量变流器接入直流配电网时,系统模型阶次升高,变流器控制策略和控制参数对电力电子化系统的稳定性产生显著影响[21-22]。为说明下垂斜率优化过程中考虑小干扰稳定约束的必要性,选取标况下的光伏及负荷数据,两台光伏出力均为额定值50 kW,负荷1,2,3的功率依次为50,100,100 kW。基于光伏负荷数据优化得到下垂参考点,将其代入状态矩阵中,可计算得到直流配电网小信号状态矩阵的特征值分布。主导特征值分布主要受下垂环节参数影响,其中下垂斜率的影响起决定性作用[8]。为说明下垂斜率变化对主导特征值的影响,令3台VSC下垂斜率相同,从0开始逐渐增大到0.037 5(标幺值),复平面上3个主导特征值的变化曲线如图2所示。由图2可知,随着下垂斜率增大,主导特征值逐渐右移,当下垂斜率k增大到0.03时有一对主导特征值实部由负变正,系统在稳态运行点小干扰不稳定。由此说明,下垂斜率合理取值对于系统安全稳定运行具有重要意义。

在Simulink中搭建直流配电网仿真模型来验证上述特征值分析。k取0.029和0.03时,直流配电网节点电压仿真对比曲线见附录F。可知,k取0.029时系统能在稳态点保持稳定运行,而k增大到0.03时电压出现振荡,振荡频率约为307 Hz,系统小干扰不稳定,与特征值分析结果一致。

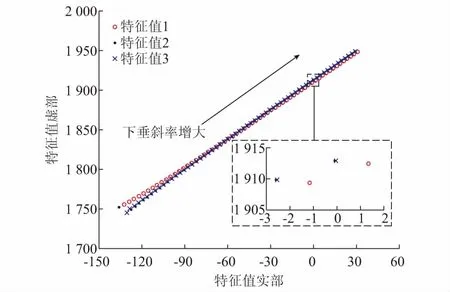
图2 主导特征值随下垂斜率变化曲线Fig.2 Curves of dominant eigenvalues when droop gains vary

4.2 模型调控效果说明

在小信号状态空间方程的基础上,对长期预测数据和短期预测数据进行蒙特卡洛仿真模拟。选取一组典型长期预测数据,光伏1和光伏2的功率分别为30 kW和40 kW。负荷1,2,3的功率分别为30,50,60 kW。下文中均采用该组长期预测数据作为下垂参考点的优化输入数据。

基于长期预测数据优化得到下垂参考点指令[5],详见附录F表F1。假设短期预测数据在长期预测数据基础之上存在±20%的波动,随机生成300组短期预测数据。分别采用以下3种方法对下垂斜率进行优化。值得说明的是,在算例分析中3台VSC的下垂斜率均为独立优化变量,其最终优化下垂指令不一定相同。

方法1:采用基于改进策略的算法进行基于极端场景的鲁棒下垂斜率优化(本文所提出的模型)。

方法2:采用基于改进策略的算法进行基于确定性预测场景的下垂斜率优化。

方法3:进行不考虑小干扰稳定约束的下垂斜率优化,采用内点法求解。

以特征值最大实部作为系统稳定性衡量标准,以网损改善率作为系统经济性衡量标准。定义网损改善率为基准网损和优化后系统网损之差与基准网损的比值。基准网损计算见附录G。将方法3的优化下垂指令分别代入各场景下的状态矩阵中进行校验,300组场景中有37组特征值越限,系统小干扰不稳定比例为12.3%。图3展示了这37组场景下,方法2和方法3的优化结果在对应预测场景中的特征值最大实部对比。由图3可知,方法2得到的下垂指令在所有确定性短期预测场景中均能保证系统小干扰稳定运行,由此说明在下垂斜率优化中考虑小干扰稳定约束至关重要。

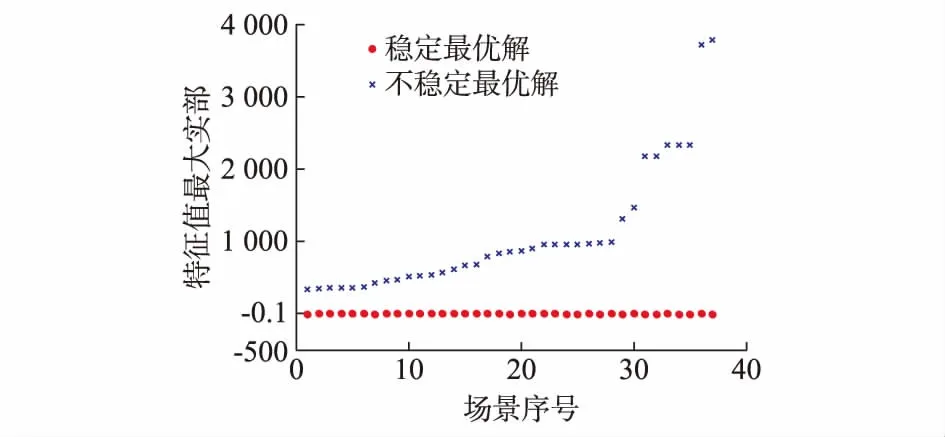
图3 稳定最优解与不稳定最优解特征值最大实部对比Fig.3 Maximal real part comparison of eigenvalues of stable optimal results and unstable optimal results

为说明基于极端场景优化得到的下垂指令的调控效果,令光伏和负荷实际功率在短期预测数据之上叠加±20%的误差,每组短期预测数据由蒙特卡洛方法随机产生200组实际源荷场景,共60 000组实际源荷场景。将方法2的300组优化指令代入对应实际场景中进行稳定性校验,结果表明有45组优化指令在实际光伏负荷场景下特征值越限,系统小干扰不稳定比例为22.5%。

采用方法1对45组不稳定下垂斜率重新进行优化。图4展示了方法2和方法1的优化指令在实际场景中的特征值最大实部对比。由图4可知,基于极端场景的下垂指令在所有光伏负荷实际场景下均能保证系统小干扰稳定,系统实际运行稳定性得到显著提升。

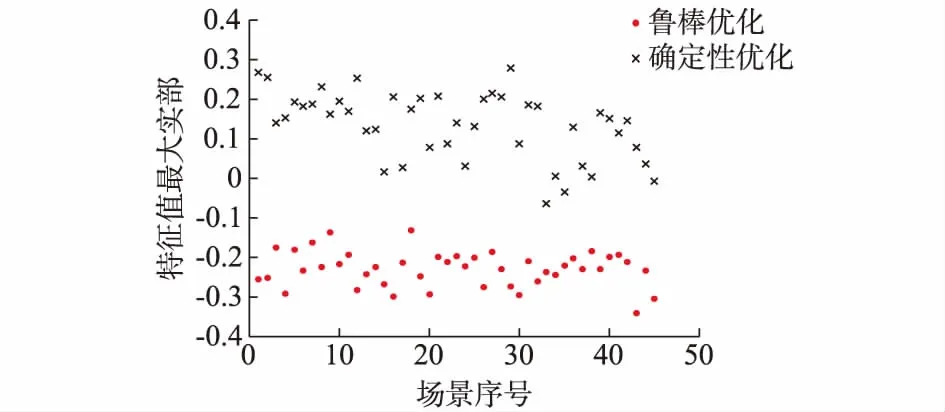
图4 确定性优化与鲁棒优化特征值最大实部对比Fig.4 Maximal real part comparison of eigenvalues of deterministic optimal results and robust optimal results

限于篇幅,3种方法下系统运行经济性的详细对比见附录H。综上所述,在下垂斜率优化模型中加入小干扰稳定约束,其最优下垂指令能在确定性预测数据下保证系统的小干扰稳定运行。基于极端场景的小干扰稳定约束能显著提高系统应对不确定源荷功率随机波动的鲁棒性,在短期预测依然存在误差的情况下,可以完全保证系统稳定且留有设定的稳定裕度,以较小的经济代价换取系统安全性的显著提升。

4.3 算法改进策略效果比较

为说明本文算法改进策略的作用效果,对300组短期预测数据采用下述方法进行下垂斜率优化。

方法4:采用基于矩阵摄动理论的序列非线性规划算法进行基于极端场景的下垂斜率优化。

方法5:采用改进遗传算法进行基于极端场景的下垂斜率优化。

表1展示了方法1,4,5这3种不同算法的求解数据统计结果。

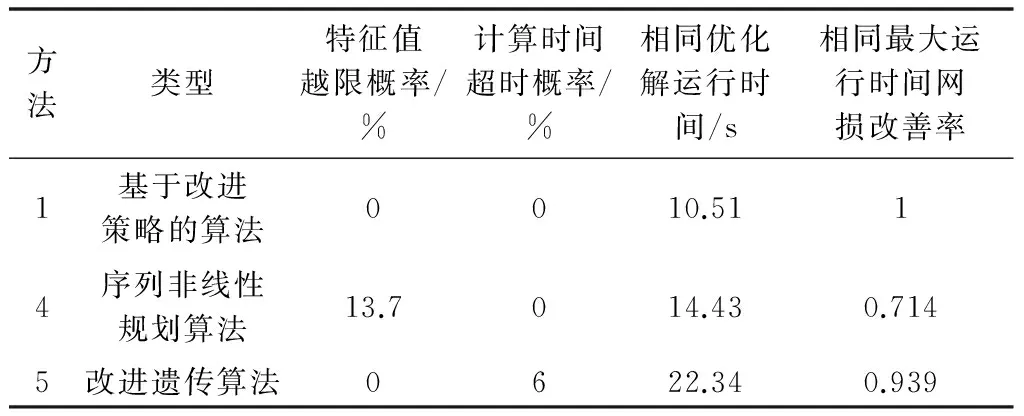
表1 算法比较Table 1 Comparison of different algorithms

表1中以方法1的优化结果作为基准值,将网损改善率进行标幺化表示。算法运行时间对比中迭代停止条件如下式所示:

|o-omin|

(15)

式中:omin为方法1的最优目标函数值;o为另外两种传统算法在迭代过程中的目标函数值;d为目标函数收敛阈值。当式(15)满足时,即认为目标函数相同,停止迭代,记录此时优化程序运行时间。定义特征值越限概率为由于特征值累计误差,对优化指令进行校验时实际系统小干扰不稳定的场景占总场景的比例。本文算例中要求下垂斜率优化程序运行时间小于1 min,定义计算时间超时概率为优化时间超过1 min的场景占总场景的比例。

由表1可知,改进遗传算法可在较短时间内将种群迅速聚集在局部最优解附近,而后可能陷入早熟,收敛性下降,导致寻优过程迅速放缓,整体优化时间较长。基于矩阵摄动理论的序列非线性规划算法虽然收敛曲线更加平滑,但特征值近似误差和单次迭代摄动率约束限制了其寻优能力和计算效率。

由特征值越限概率对比可说明改进策略2)的作用效果。单独采用基于矩阵摄动理论的序列非线性规划算法时,由于特征值近似误差积累,采用QR法对特征值进行校验时,300组场景下有41组场景特征值越限,优化得到的下垂指令实际小干扰不稳定,特征值越限概率为13.7%。而方法1不存在特征值越限问题。

由计算时间超时概率和相同优化解运行时间对比可说明改进策略3)的作用效果。方法4优化解相同时算法平均运行时间为14.43 s,方法5在300组场景优化中有18组场景1 min内目标函数不收敛,计算时间超时概率为6%,优化解相同时算法平均运行时间为22.34 s。而方法1在该策略下,优化解相同时算法平均运行时间为10.51 s,且不存在计算时间超时问题,计算效率得到显著提高。

由相同最大运行时间下的网损改善率对比可间接说明改进策略1)的作用效果。由于表1中所比较的3种非线性优化问题求解算法较难从理论上证明其解的全局最优性,因而只能通过比较相同运行时间下的网损改善率来间接衡量不同算法的寻优能力。相同最大运行时间下,以方法1的网损改善率为基准,方法1比方法4网损改善率平均提高28.6%,比方法5网损改善率平均提高6.1%。可见,方法1与其他两种算法相比有更强的寻优能力。

综上所述,本文在序列非线性规划算法和遗传算法的基础上提出相应改进策略,结合了二者算法的优点,利用遗传算法迅速找到次优解,并在次优解的基础上进行矩阵摄动迭代,能较为快速准确地找到更优的解或最优解,所提出的改进策略能在保证优化结果可靠有效的前提下提高算法的寻优能力和计算效率。

5 结语

本文以下垂控制模式下含AC/DC和DC/DC变流器的环状直流配电网为研究对象,建立了直流配电网状态空间模型,分析了下垂参数对系统小干扰稳定性的影响。基于状态空间模型提出了考虑小干扰稳定约束的直流配电网下垂参数优化调控模型。数值实验结果表明以下几点。

1)基于极端场景的小干扰稳定约束能使得优化下垂调控指令以较小的经济代价大幅提升系统适应不确定性源荷功率随机波动时的鲁棒性。

2)为求解该优化模型,在遗传算法和序列非线性规划算法的基础上,提出了改进策略,能在保证优化结果可靠有效的同时,提高算法的寻优能力和计算效率。

下一步工作考虑进一步丰富完善不确定条件下系统的鲁棒经济优化调度模型。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 雍静,徐欣,曾礼强,等.低压直流供电系统研究综述[J].中国电机工程学报,2013,33(7):42-52.

YONG Jing, XU Xin, ZENG Liqiang, et al. A review of low voltage DC power distribution system[J]. Proceedings of the CSEE, 2013, 33(7): 42-52.

[2] 马骏超,江全元,余鹏,等.直流配电网能量优化控制技术综述[J].电力系统自动化,2013,37(24):89-96.

MA Junchao, JIANG Quanyuan, YU Peng, et al. Survey on energy optimized control technology in DC distribution network[J]. Automation of Electric Power Systems, 2013, 37(24): 89-96.

[3] 王成山,李琰,彭克.分布式电源并网逆变器典型控制方法综述[J].电力系统及其自动化学报,2012,24(2):12-20.

WANG Chengshan, LI Yan, PENG Ke. Overview of typical control methods of grid-connected inverters of distributed generation[J]. Proceedings of the CSU-EPSA, 2012, 24(2): 12-20.

[4] 吕振宇,吴在军,窦晓波,等.自治直流微电网分布式经济下垂控制策略[J].中国电机工程学报,2016,36(4):900-910.

LÜ Zhenyu, WU Zaijun, DOU Xiaobo, et al. A distributed droop control scheme for islanded DC microgrid considering operation costs[J]. Proceedings of the CSEE, 2016, 36(4): 900-910.

[5] MA J, GENG G, JIANG Q. Two-time-scale coordinated energy management for medium-voltage DC systems[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3971-3983.

[6] 刘念,李岩松,张建华,等.微电网互联运行的分时优化与实时控制方法[J].电工技术学报,2016,31(21):1-11.

LIU Nian, LI Yansong, ZHANG Jianhua, et al. Hour-ahead optimization and real-time control method for micro-grid interconnection[J]. Transactions of China Electrotechnical Society, 2016, 31(21): 1-11.

[7] WANG Chengshan, LI Yan, PENG Ke, et al. Coordinated optimal design of inverter controllers in a micro-grid with multiple distributed generation units[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2679-2687.

[8] BARKLUND E, POGAKU N, PRODANOVIC M, et al. Energy management in autonomous microgrid using stability-constrained droop control of inverters[J]. IEEE Transactions on Power Electronics, 2008, 23(5): 2346-2352.

[9] 邢洁,陈陈,武鹏.考虑小干扰稳定约束的有功优化调度[J].电力系统自动化,2010,34(12):24-28.

XING Jie, CHEN Chen, WU Peng. Optimal active power dispatch with small-signal stability constraints[J]. Automation of Electric Power Systems, 2010, 34(12): 24-28.

[10] 李佩杰,韦化,白晓清.小干扰稳定约束最优潮流的非线性半定规划方法[J].中国电机工程学报,2013,33(7):69-76.

LI Peijie, WEI Hua, BAI Xiaoqing. Small-signal stability constrained optimal power flow based on NLSDP[J]. Proceedings of the CSEE, 2013, 33(7): 69-76.

[11] 李岩,易越,李巍巍,等.直流配电系统对可再生能源的消纳能力分析[J].南方电网技术,2017,11(3):46-52.

LI Yan, YI Yue, LI Weiwei, et al. Analysis on ability of renewable energy consumption of DC distribution system[J]. Southern Power System Technology, 2017, 11(3): 46-52.

[12] 金阳忻,徐习东.采用下垂控制的直流配电网小干扰稳定性分析[J].电力系统自动化,2016,40(14):78-85.DOI:10.7500/AEPS20150805006.

JIN Yangxin, XU Xidong. Small-signal stability analysis of DC distribution network adopting droop control[J]. Automation of Electric Power Systems, 2016, 40(14): 78-85. DOI: 10.7500/AEPS20150805006.

[13] POGAKU N, PRODANOVIC M, GREEN T C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 613-625.

[14] 向阳,付明,张爱芳,等.孤岛运行的交直流混合微电网小信号稳定性分析[J].电力建设,2017,38(1):96-105.

XIANG Yang, FU Ming, ZHANG Aifang, et al. Small signal stability analysis of AC/DC hybrid microgrid under isolated island operation[J]. Electric Power Construction, 2017, 38(1): 96-105.

[15] GÜNEL S, ZORAL E Y. Parametric history analysis of resonance problems via step-by-step eigenvalue perturbation technique[J]. IET Microwaves Antennas Propagation, 2010, 4(4): 466-476.

[16] 赵书强,陈慷,马燕峰,等.密集型固有振荡模式电力系统的模态分析[J].电力系统自动化,2011,35(21):6-11.

ZHAO Shuqiang, CHEN Kang, MA Yanfeng, et al. Modal analysis of electric power system with close oscillation modes[J]. Automation of Electric Power Systems, 2011, 35(21): 6-11.

[17] 黄一诺,郭创新,王力成,等.考虑用户满意度的电动汽车分群调度策略[J].电力系统自动化,2015,39(17):183-191.DOI:10.7500/AEPS20150331011.

HUANG Yinuo, GUO Chuangxin, WANG Licheng, et al. A cluster-based dispatch strategy for electric vehicles considering user satisfaction[J]. Automation of Electric Power Systems, 2015, 39(17): 183-191. DOI: 10.7500/AEPS20150331011.

[18] 叶承晋,黄民翔,陈丽莉,等.基于并行非支配排序遗传算法的限流措施多目标优化[J].电力系统自动化,2013,37(2):49-55.

YE Chengjin, HUANG Minxiang, CHEN Lili, et al. Multi-objective current limiters configuration based on parallel fast and elitist non-dominated sorting genetic algorithm-Ⅱ[J]. Automation of Electric Power Systems, 2013, 37(2): 49-55.

[19] 威尔金森J H.代数特征值问题[M].石钟慈,邓健新,译.北京:科学出版社,2001:64-108.

[20] 盛万兴,李蕊,李跃,等.直流配电电压等级序列与典型网络架构初探[J].中国电机工程学报,2016,36(13):3391-3403.

SHENG Wanxing, LI Rui, LI Yue, et al. A preliminary study on voltage level sequence and typical network architecture of direct current distribution network[J]. Proceedings of the CSEE, 2016, 36(13): 3391-3403.

[21] 宋国兵,陶然,李斌,等.含大规模电力电子装备的电力系统故障分析与保护综述[J].电力系统自动化,2017,41(12):2-12.DOI:10.7500/AEPS20170502006.

SONG Guobing, TAO Ran, LI Bin, et al. Survey of fault analysis and protection for power system with large scale power electronic equipments[J]. Automation of Electric Power Systems, 2017, 41(12): 2-12. DOI: 10.7500/AEPS20170502006.

[22] 朱蜀,刘开培,秦亮,等.电力电子化电力系统暂态稳定性分析综述[J]. 中国电机工程学报,2017,37(14):3948-3962.

ZHU Shu, LIU Kaipei, QIN Liang, et al. Analysis of transient stability of power electronics dominated power system: an overview[J]. Proceedings of the CSEE, 2017, 37(14): 3948-3962.

孙峰洲(1994—),男,博士研究生,主要研究方向:配电网与微电网能量管理、运行控制。E-mail： 11610028@zju.edu.cn

马骏超(1989—),男,博士,主要研究方向:配电网能量管理。E-mail: majunchao1989@gmail.com

朱 洁(1972—),女,硕士,教授级高级工程师,主要研究方向:新能源及电动汽车领域。E-mail: zhujie11@sina.com

于 淼(1984—),男,通信作者,博士,副教授,主要研究方向:配电网与微电网运行控制。E-mail: zjuyumiao@zju.edu.cn