基于不确定测度的电力系统抗差状态估计(三)算法对比

陈艳波, 谢瀚阳, 王 鹏, 王金丽, 葛 婷, 王若兰

(1. 华北电力大学电气与电子工程学院, 北京市 102206; 2. 广东电网有限责任公司信息中心, 广东省广州市 510600; 3. 中国电力科学研究院有限公司, 北京市 100192)

国家自然科学基金资助项目(51777067);中央高校基本科研业务费专项资金资助项目(2016YQ02)。

0 引言

本文是该系列文章的第3篇。第2篇在不确定理论体系下,以不确定测度为基础,提出了基于兼顾测点正常率的偏离度最小准则的最大正常率最小偏差度(maximum normal-rate least deviation,MNLD)估计方法[1]。本文将对MNLD方法与已有的状态估计(state estimation,SE)方法进行详细的分析对比。

已有的SE方法中,加权最小二乘(WLS)估计[2]以其数学模型简洁、计算方法简单得到广泛应用。WLS估计假定量测误差服从正态分布,是加权最小方差无偏估计。但是,实际量测误差不一定服从正态分布,此时WLS估计结果没有理论上的保证;WLS估计在使用时需要加上一个基于残差的不良数据辨识环节,如最大标准化残差(largest normal residual,LNR)法,但WLS+LNR对强相关的多不良数据的辨识能力有限。

抗差状态估计(robust state estimation,RSE)在估计过程中可以自动抑制不良数据。加权最小绝对值(weighted least absolute value,WLAV)[3]是基于残差的绝对值最小准则;QC(quadratic-constant)准则[4]是假定一个阈值,将正常量测残差视作正态分布,异常量测残差视作均匀分布,以此赋大小权。基于测量不确定度的最大正常测点率(maximum normal measurement rate,MNMR)[5-7]的思想是通过量测值是否落入测量不确定区间来区分量测数据的“好坏”。

已有SE方法主要建立在概率统计体系下大数定律或测量不确定度的理论基础上。由于实际系统中量测量的数目有限,直接使用小样本或者假定主观先验概率去应用概率统计的数学系统进行计算和求解,估计结果的精度没有理论上的保证。

不确定测度能够合理地处理主观信息[8],本文通过对基于不确定测度的MNLD估计方法与已有的SE方法进行了多个方面的对比,并进行了系统的分析。

1 估计方法比较

电力SE在数学上需要求解一个优化问题,其模型可以统一表示为:

(1)

式中:Fn(·)为ρi的函数;m为系统的量测量个数;Z为m维量测量向量;x为状态向量;h(·)为量测函数向量;ρ为m维量测误差向量;ρi为ρ向量中第i个元素,即第i个测点的测量误差。

不同的估计方法,在于Fn(·)函数的不同。

1.1 WLS估计

WLS估计采用的是残差的加权平方和最小的准则函数,Fn(·)的形式为:

(2)

式中:ωi为第i个测点的权重。

WLS估计对严格服从正态分布的数据为无偏估计。当实际量测误差不服从正态分布时,WLS估计将失去无偏估计的优良性能;WLS估计本身无抗差能力,在使用时常使用WLS+LNR等方法。

1.2 WLAV估计

WLAV估计采用的是残差的绝对值之和最小的准则函数,Fn(·)的形式为:

Fn(ρi)=ωi|ρi|

(3)

WLAV估计方法是量测误差服从拉普拉斯分布时的极大似然估计。在误差分布不服从拉普拉斯分布时,不是最优估计。WLAV估计具有抗差性,但易受杠杆点不良数据的影响[9]。

1.3 QC非二次准则

QC估计对残差进行分段处理,残差较小时以残差的加权平方和最小为目标函数,残差较大时则特殊处理,Fn(·)的形式为:

(4)

式中:σi为第i个测点的不良数据判定的阈值。

QC估计从目标函数的形式来看,可以看作是假定了正常量测时误差服从正态分布,异常量测时误差服从均匀分布的极大似然估计的近似。以阈值的形式判别不良数据,使得QC非二次准则具有抗差性,但是仍不能排除杠杆量测。

1.4 MNMR估计

MNMR估计引入测量不确定度的概念,定义了正常测点和正常测点率,以正常测点率最高为目标函数,其理想模型为:

(5)

式中:Ui为置信概率p对应的第i个测点的扩展不确定度;g(·)为测点评价函数,有

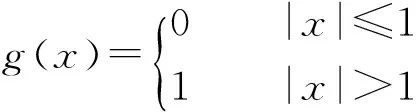
(6)

MNMR估计的目标函数不只是与残差相关,还与测量不确定度相关,若对MNMR理想模型作如下等价变换:

(7)

其中

(8)

这样,目标函数将变成广义的残差函数,Fn(·)的形式为:

Fn(ρi)=geq(ρi)

(9)

文献[10]指出,经过变换后的MNMR估计模型,从目标函数的形式上看,该模型是认为测量噪声服从自适应的均匀分布,通过均匀分布的阈值判别量测量是否为不良数据[11]。而阈值是由基于统计方法得到的测量不确定度决定的,这使得MNMR估计在大样本估计问题中具有较好的抗差性。

1.5 MNLD估计

在数学上MNLD估计是多目标规划问题,它在不确定理论下以测点正常率和量测值偏离估计值程度最小为目标,其理想的目标函数为:

(10)

其中

(11)

θi为测点i量测噪声不确定分布下置信水平为α对应的不确定度。

MNLD估计从第1个目标函数的形式上看,也是首先认为测量噪声服从自适应的均匀分布,通过均匀分布的阈值判别是否为不良数据。其阈值是根据极大熵原理确定分布类型后得到的,因此其自适应性是来自使用于小样本或没有样本的不确定测度,具有较强的抗差性。

从第2个目标函数的形式上看,MNLD估计进一步将剔除了不良数据后的量测值进行最小最大绝对值估计,Fn(·)的形式为:

Fn(ρj)=max(|ρj|)j∈N(1)

(12)

式中:N(1)为正常测点集。

本文对MNLD估计方法,以及上述的WLS,WLAV,QC和MNMR估计方法的性能进行对比测试,分别用IEEE 9,14,30,39,57,118,300节点及实际电网算例进行仿真试验。计算机试验条件为:PC机,DELL,CPU为Intel(R) Core(TM) i5-4590、主频为3.30 GHz、内存4.00 GB,算法采用Java编程。

2 抗差性试验

本节将所提出的MNLD估计方法与已有的常用估计方法WLS,WLAV,QC和MNMR进行抗差性能的对比研究。其中WLS估计不具有抗差性,在WLS估计之后利用LNR法辨识不良数据。

针对电网运行实际可能遇到的一般性不良数据,以及难以处理的强相关的多不良数据和杠杆点不良数据,本节分别采用不同的估计方法对IEEE 9,14,30,39,118节点系统进行仿真试验,包括SE效果、迭代次数和计算时间等。

SE效果的评价指标除了采用本系列文章第1篇所提出的不确定理论下的测点正常率η和考虑测点正常率的偏离度Δn-m进行评价外,对参与正常测量的测点再采用偏差的平均绝对值S1和无穷范数Smax进行评价[12]:

(13)

(14)

S1和Smax分别用以衡量正常测点估计值与真值的整体偏差和最大偏差。

2.1 一般不良数据辨识

通过将潮流计算的结果分别加上2%的高斯噪声或服从均匀分布的噪声,再将部分数据通过符号置反、置零、加减20%以上的手段变为不良数据,得到含不良数据的测量数据。本实验采用IEEE 14节点系统(见附录A图A1),其中包含量测量110个,添加不良数据10个。表1和表2分别给出了加正态分布噪声和均匀分布噪声的IEEE节点的实验结果,图1和图2分别给出了抗差性表现良好的MNLD,MNMR和WLAV抗差估计方法在含正态分布噪声和均匀分布噪声时的估计残差分布。

表1 含正态分布噪声和不良数据的IEEE系统估计结果Table 1 Estimation result of IEEE system containing bad data and noise with normal distribution

表2 含均匀分布噪声和不良数据的IEEE系统估计结果Table 2 Estimation result of IEEE system containing bad data and noise with uniform distribution

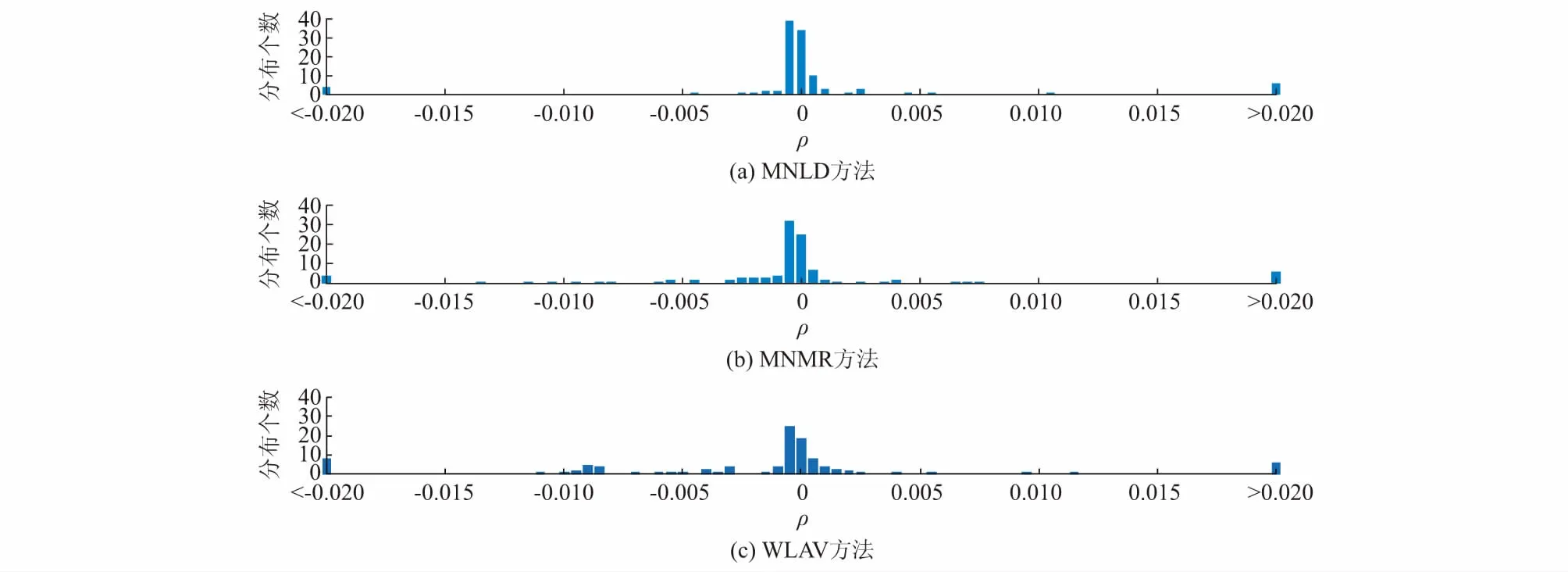
图1 含正态分布噪声的IEEE系统估计残差分布Fig.1 Residual distribution in IEEE system containing noise with normal distribution

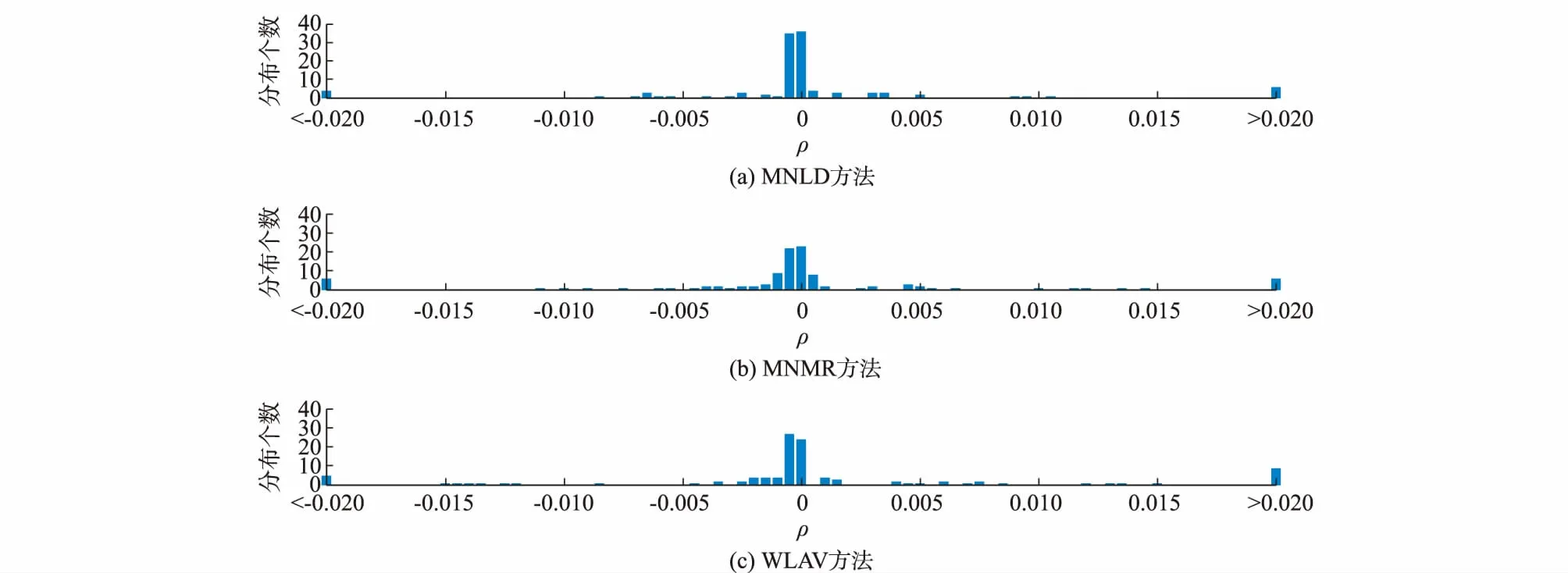
图2 含均匀分布噪声的IEEE系统估计残差分布Fig.2 Residual distribution in IEEE system containing noise with uniform distribution

从表1、表2试验结果可以得出以下结论。

1)量测噪声符合高斯分布时,MNLD方法、MNMR方法和WLS+LNR方法的结果指标η和S1基本相同,而且优于其他两种方法,而MNLD方法的指标Δn-m和Smax优于MNMR方法和WLS+LNR方法;WLAV方法和QC方法次之。

2)量测噪声符合均匀分布时,MNLD方法结果的合理性最优,基本与含正态分布噪声时的结果一致;MNMR方法、WLS+LNR方法和WLAV方法次之,其估计性能不如含正态分布噪声时的表现,特别是指标η和S1;QC方法次之。

3)RSE方法WLAV,MNMR和MNLD的迭代次数与WLS相差不大,QC方法迭代次数相对较多,说明WLAV,MVMR和MNLD方法具有较高的计算效率。

需要指出的是,如图1(a)和(b)所示,在量测噪声符合高斯(正态)分布时,MNLD方法的指标Δn-m和Smax优于MNMR和WLS+LNR方法。这是因为MNLD方法进一步将正常测点的量测值进行最小最大绝对值估计,使得正常量测值偏离估计值最小,残差更集中地分布在0附近,如图1(a)所示,因此其估计结果合理性更好。

而在量测噪声符合均匀分布时,因为相同信噪比下服从均匀分布的噪声的方差比高斯噪声的方差大,而直接与方差相关的测量不确定度因此受到影响,使得基于测量不确定度的MNMR方法的正常测点判据与实际存在偏差,极端情况下可能会将正常量测误判为异常量测,因此合理性下降;WLS+LNR方法因为不良数据辨识是基于残差并假定噪声服从正态分布,也会因为相同的原因导致合理性下降;而基于不确定测度的MNLD方法能合理处理先验信息,使得正常测点判据自适应于实际情况,因此合理性较优。

2.2 强相关多不良数据辨识

强相关不良数据是指不良数据之间存在高度的相关性。强相关不良数据会引起SE结果偏离实际,是电力系统SE的难题。

本节通过将IEEE 14节点系统潮流计算的结果分别加上3%服从正态分布的噪声,再将节点5注入有功功率P5,以及线路5-1首端、线路5-2首端和线路5-4首端有功功率P5-1,P5-2,P5-4按相同比例系数缩小,得到含强相关不良数据的测量数据。含强相关不良数据的IEEE系统量测值与MNLD估计值如附录A表A1所示。对具有抗差性的MNLD,MNMR,WLAV和QC方法进行测试,各个方法的估计结果如表3所示。

表3的估计试验结果表明,MNLD方法和MNMR方法在面对含强相关多不良数据的系统时,估计结果的测点正常率最高,对强相关多不良数据抑制效果显著,但MNLD方法的SE结果评价指标Δ106-110优于MNMR方法,因此MNLD方法的估计结果更具合理性。WLAV方法合理性次之,其节点5注入有功功率的估计结果受到强相关不良数据的严重影响。QC估计方法面对含强相关不良数据的系统时,估计结果严重偏离实际。

表3 含强相关不良数据的IEEE系统估计结果Table 3 Estimation result of IEEE system containing bad data with strong correlation

2.3 杠杆点不良数据辨识

在SE中,杠杆点不良数据会给基于残差的不良数据识别及一般的抗差SE算法带来严峻的挑战。以一个IEEE 14节点系统为例,潮流计算结果分别加上3%的服从正态分布的噪声,通过改变线路2-5的线路阻抗使得线路2-5首端有功功率和无功功率成为杠杆量测,再在杠杆量测中加入不良数据,对具有抗差性的MNLD,WLAV,QC和MNMR方法进行测试,表4所示为各个方法的估计结果。

表4 含杠杆点不良数据的IEEE系统估计结果Table 4 Estimation result of IEEE system containing bad data at leverage point

表4的估计试验结果表明,MNLD和MNMR方法在面对含杠杆点不良数据的系统估计结果合理性相当,能抑制杠杆点不良数据,但MNLD方法的结果评价指标小于MNMR方法,因此MNLD方法的SE结果更具合理性。WLAV,QC和WLS方法在面对含杠杆点不良数据的系统时,估计结果严重偏离实际。

3 计算效率对比试验

为了进行计算效率比较,本节在正常量测条件下分别对5种SE方法WLS,WLAV,QC,MNMR及MNLD进行了测试。在试验中,WLS采用牛顿法求解,其他3种SE采用内点法求解。SE收敛时的迭代次数及平均计算耗时如表5所示。

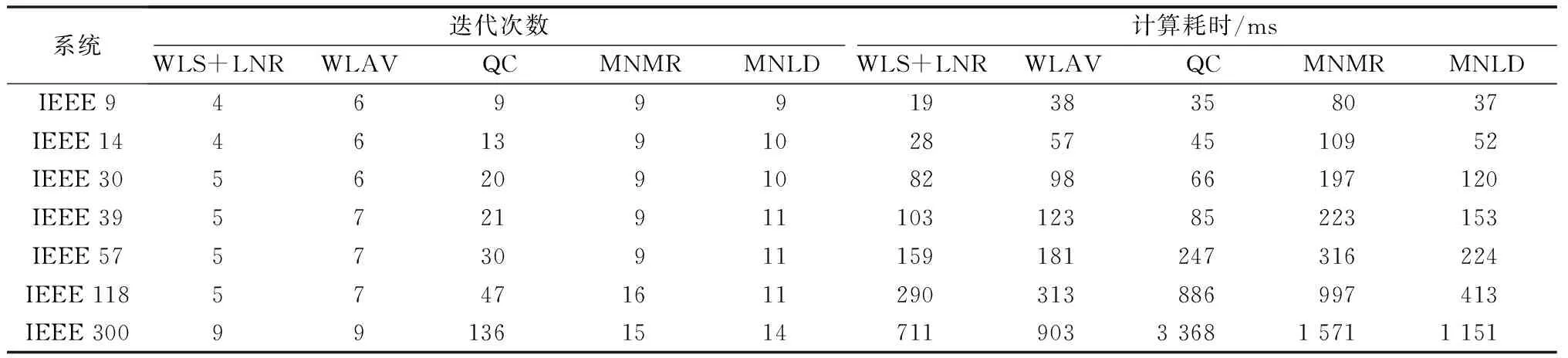
表5 迭代次数与计算耗时的对比Table 5 Comparison of iteration times and calculation time

由表5可见,在这5种状态估计器中,WLS的计算效率最高;而在后4种抗差状态估计器中,MNLD,MNMR和WLAV方法的计算效率较高;而且随着系统规模的增大,MNLD方法的迭代次数及计算耗时增长缓慢,因而MNLD方法适用于实际的大规模系统的估计。

4 实际运行情况

利用东北某实际电网的实际数据断面,应用WLS,WLAV,QC,MNMR及MNLD方法进行SE的计算结果如表6所示。可以看出,MNLD在测点正常率和量测量偏离估计值的程度上都有很大的提高,其合理性优于其他算法。

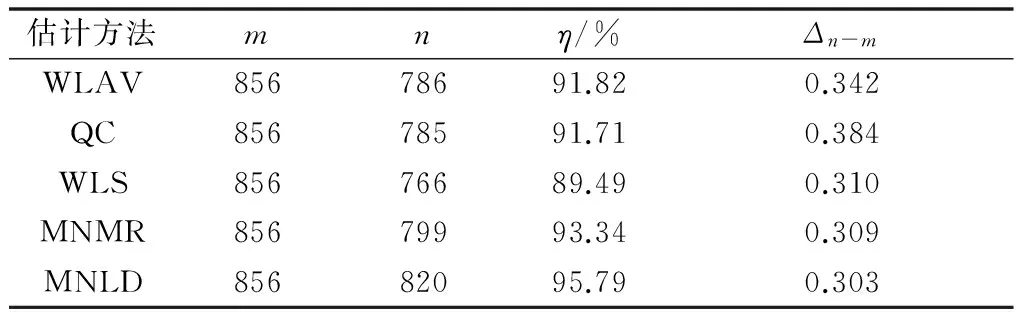
表6 实际电网数据估计结果Table 6 Estimation results of practical data in power grid

5 结语

本文对基于不确定测度提出的MNLD估计方法与已有的估计方法WLS,WLAV,QC和MNMR进行了抗差性、计算效率的对比研究分析。测试结果表明如下。

1)在抗差性能上,MNLD方法对强相关的多不良数据和杠杆点不良数据均具有较强的抑制能力,其抗差性能优于基于残差的传统SE方法和基于测量不确定度的MNMR方法。

2)在计算效率上,MNLD方法计算效率较高,而且随着系统规模的增大,MNLD方法的迭代次数及计算耗时增长缓慢,因而对实际的大规模电力系统的SE,MNLD方法有其应用价值。

值得指出的是,本系列文章所提出的基于不确定测度的MNLD估计方法具有非线性特性,因此对于高阻抗比的电力系统,其收敛性不如WLS方法,如何提高MNLD方法对于高阻抗比电力系统的适应性是下一步的研究方向。同时,仅当不良数据、拓扑错误和参数错误被同时辨识出时,SE才能得到可信的估计结果,如何基于MNLD方法进行状态、拓扑和参数的综合估计也是下一步的研究方向。

本文得到国家自然科学基金项目(51407069)资助,谨此致谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 陈艳波，谢瀚阳，王鹏，等.基于不确定测度的电力系统抗差状态估计：(二)模型方法[J].电力系统自动化，2018，42(2):26-33.DOI:10.7500/AEPS20161213007.

CHEN Yanbo, XIE Hanyang, WANG Peng, et al. Uncertain measure based robust state estimation of power system: Part two model and solution[J]. Automation of Electric Power Systems, 2018， 42(2): 26-33. DOI: 10.7500/AEPS20161213007.

[2] SCHWEPPE F C, WILDES J. Power system static-state estimation: Part Ⅰ, Ⅱ, Ⅲ[J]. IEEE Transactions on Power Apparatus and System, 1970, 89(1): 120-135.

[3] CELIK M K, ABUR A, MELIOPOULOS A P, et al. A robust WLAV state estimator using transformations[J]. IEEE Transactions on Power Systems, 1992, 7(1): 106-113.

[4] BALDICK R, CLEMENTS K A, PINJO-IAZIGAL Z, et al. Implementing non-quadratic objective functions for state estimation and bad data rejection[J]. IEEE Transactions on Power Systems, 1997, 12(1): 376-382.

[5] 何光宇,董树锋.基于测量不确定度的电力系统状态估计:(一)结果评价[J].电力系统自动化,2009,33(19):21-24.

HE Guangyu, DONG Shufeng. Power system static-state estimation based on uncertainty of measurement: Part one result evaluation[J]. Automation of Electric Power Systems, 2009, 33(19): 21-24.

[6] 何光宇,董树锋.基于测量不确定度的电力系统状态估计:(二)方法研究[J].电力系统自动化,2009,33(20):32-36.

HE Guangyu, DONG Shufeng. Power system static-state estimation based on uncertainty of measurement: Part two a new method[J]. Automation of Electric Power Systems, 2009, 33(20): 32-36.

[7] 何光宇,董树锋.基于测量不确定度的电力系统状态估计:(三)算法比较[J].电力系统自动化,2009,33(21):28-31.

HE Guangyu, DONG Shufeng. Power system static-state estimation based on uncertainty of measurement: Part three algorithms compared[J]. Automation of Electric Power Systems, 2009, 33(21): 28-31.

[8] LIU B. Uncertainty theory[M]. Berlin, Germany: Springer, 2007.

[9] CHEN Yanbo, LIU Feng, MEI Shengwei, et al. A robust WLAV state estimation using optimal transformations[J]. IEEE Transactions on Power Systems, 2015, 30(4): 2190-2191.

[10] 陈艳波,马进,文一宇.一种电力系统量测噪声自适应抗差状态估计方法[J].电力系统自动化,2015,39(8):66-73.DOI:10.7500/AEPS20140402006.

CHEN Yanbo, MA Jin, WEN Yiyu. An adaptive robust state estimation approach for measurement noise[J]. Automation of Electric Power Systems, 2015, 39(8): 66-73. DOI: 10.7500/AEPS20140402006.

[11] 陈艳波.基于统计学习理论的电力系统状态估计研究[D].北京:清华大学,2013.

[12] KOTIUGA W W, VIDYASAGAR M. Bad data rejection properties of weighted least absolute value techniques applied to static state estimation[J]. IEEE Transactions on Power Apparatus and Systems, 1982, 101(4): 844-853.

陈艳波(1982—),男,通信作者,博士,副教授,硕士生导师,主要研究方向:电力系统状态估计、信息安全、综合能源系统。E-mail： yanbochen2008@sina.com

谢瀚阳(1992—),男,硕士研究生,主要研究方向:电力系统状态估计。

王 鹏(1982—),男,硕士,主要研究方向:配电网调度自动化系统。

(编辑章黎)

( continuedonpage47)( continuedfrompage13)