泛圈图的谱条件

汪 健，王礼想，夏祥伟，于 涛

(安庆师范大学数学与计算科学学院，安徽安庆 246133)

设G=(V,E)是一个n个顶点m条边的图，如果G中边是没有方向的，而且G中无环无重边以及任意两点都存在一条路，则称G为简单无向连通图。本文讨论的图都是简单无向连通图。设G是一个由顶点集V(G)={v1,v2,…,vn}和边集E(G)={e1,e2,…,en}构成的图。对于任意的vi∈V(G)，我们用d(vi)或者di表示vi的度，记δ为G的顶点的最小度。若一个图的顶点集可以划分为两个非空子集X和Y，而且该图的每条边都有一个端点在X中，另一个端点在Y中，则称这样的图为二部图。在图G中，如果对于每一个k(3≤k≤n)，都含有长度为k的圈Ck，则称G为泛圈图。图G的邻接矩阵A(G)=(aij)n×n定义为：如果vi和vj相邻，则aij=1，否则aij=0。用μ(G)来表示A(G)的最大特征值，称为谱半径。令D(G)为G的度对角矩阵，称矩阵Q(G)=D(G)+A(G)是G的无符号拉普拉斯矩阵，用q(G)来表示G的无符号拉普拉斯谱半径。如果G中每对顶点都有一条边连接，则称它为完全图，记作Kn。用Kn-1+v来表示一个有n-1个顶点的完全图加上一个孤立点。我们用G∨H来表示G和H的连图，它是通过把G中的每个顶点和H中的每个顶点连接起来所获得的。

1 相关引理

引理1[4]设G是一个n阶简单图(n≥3) ，对应的一个度序列是d1≤d2≤…≤dn，如果存在整数k满足dk≤k＜时，有≥n-k。则G是一个泛圈图或二部图。

设NPC是K4∨5K1，K2∨(K3+2K1) ，K3∨4K1，K1,2∨4K1，K2∨(K1+K1,3)，K2∨(K2+2K1) ，K1∨2K2，K2∨3K1这些图的集合。显然，这些图是非泛圈的。

引理2设G是一个图，δ≥2，如果m＞，则G是一个泛圈图，除非G是一个二部图或G∈NPC。

证明：设G有n个顶点和m条边，满足δ≥2。设d1≤d2≤…≤dn是它的度序列。假设G是一个非泛圈图且非二部图，由引理1可知，如果整数k满足dk≤k＜时，有dn-k≤n-k-1。则

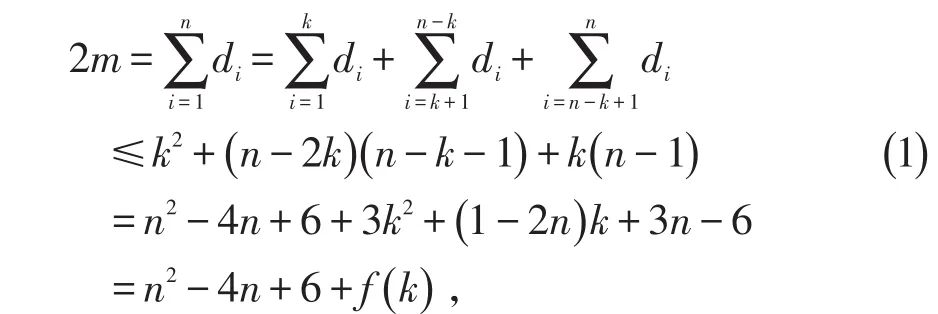
这里的f(k)=3k2+(1-2n)k+3n-6。因为n＞2k≥2dk≥2δ≥4，所以n≥5，k≥2。又因为，所以f(k) ＞0。

当2≤k＜k1时，得到

2n-13＞。然后可知n＜8。

对于n为偶数时，同样地可以得到2＜n＜8。所以n的取值只能为9，7，6，5。

n=9时，有k∈{2,3,4}。因为f(2)=-1，f(3)=-2，f(4)=1，而f(k)＞0，所以k=4。这时，d4≤4，d5≤4。又因为=2m≤52，所以=52即在不等式(1)中等号成立。此时G的度序列是(4,4,4,4,4,8,8,8,8) 。因此G≅K4∨5K1。

n=7时，有k∈{2,3}。得到f(2)=1，f(3)=3。如果k=2，根据定理条件我们知道

n=6时，有k=2 ，而18＜=2m≤20，所以=20即在不等式(1)中等号成立。此时G的度序列是(2,2,3,3,5,5,)，因此G≅K2∨(K2+2K1)。

n=5时，有k=2，而11＜=2m≤14，所以=12或14。由于d2≤2，d3≤2，有三个度序列与G对应。(2,2,2,2,4)，此时G≅K1∨2K2;(2,2,2,3,3)，此 时 G≅K2,3;(2,2,2,4,4)，此时G≅K2∨3K1。注意到G≅K2,3是二部图，且G≅K2∨(K2+K1,2)是泛圈图，与前提假设矛盾。

综上所述，定理证明结束。

引理3[5]设G是一个n阶m条边的连通图，则，等号成立时当且仅当G是K1,n-1或Kn。

引理4[6]设G是一个n阶m条边的图，则。如果G是连通的，则等号成立时当且仅当G是K1,n-1或Kn。如果G不是连通的，等号成立时当且仅当G是Kn-1+v。

2 主要结论

定理1设G是一个顶点数n≥5的连通图，δ≥2。如果，则G是泛圈图除非G是二部图或。

证明：假设G是有m条边的非泛圈图。我们容易发现Kn是泛圈的，而δ(K1,n-1)=1，不满足δ≥2的条件。所以由引理2，我们可知，又因为定理条件要求，所以，解不等式后我们可以得到。再根据引理1，得出G是一个二部图或G∈NPC。通过直接计算(见表一)可以知道除了K3∨4K1，K2∨(K2+2K1)，K1∨2K2和K2∨3K1满足，NPC中其余的图的μ(G)都是小于。定理证明完成。

定理2设G是一个顶点数n≥5的图，δ≥2。如果q(G)≥2n-5+，则G是泛圈图除非G是二部图或G∈{K3∨4K1,K2∨3K1}。

证明：假设G是有m条边的非泛圈图。我们容易发现Kn是泛圈的，而δ(K1,n-1)=1，δ(Kn-1+v)=0，不满足δ≥2此条件。所以由引理3，我们可知。又因为，所以，解不等式后我们可以得到。再根据引理1，得出G是一个二部图或G∈NPC。通过直接计算可以知道除了K3∨4K1和K2∨3K1满足q(G)＞2n-5+，NPC中其余的图的q(G)都是小于2n-5+。定理证明完成。