脉冲型地震下隔震结构的等强度位移需求谱研究

王亚楠， 杜永峰， 胡高兴

(1.西安工业大学 建筑工程学院，西安 710021； 2.西部土木工程防灾减灾教育部工程研究中心，兰州 730050)

隔震支座作为隔震结构的重要部件，在强震作用下将经历很大的变形，如果设计不当或遭遇特殊地震作用，例如，近年来受到广泛关注的脉冲型地震动，极易发生拉裂、失稳等破坏，进而影响上部结构的抗震性能[1]。在对隔震结构进行抗震性能评估时，需要对隔震支座的位移需求进行计算，判断支座位移是否超出其变形能力范围。通常情况下，采用非线性动力时程分析法对隔震支座的位移需求进行计算，该方法虽然严谨但是较为复杂和繁琐，耗时较大，利用非弹性位移需求谱对隔震支座的最大非弹性变形进行估算是一种切实可行且非常高效的方法。

关于非弹性位移需求谱的研究，国内外已有不少文献可供参考。Borzi等[2]建立了用于求解等延性非弹性位移需求谱、位移减小因子的数学表达式以及延性系数和阻尼比之间的关系表达式。Chopra等[3]研究了非弹性单自由度体系和弹性单自由度体系峰值变形之间的关系，建立了以周期比、延性系数或强度折减系数作为参数的非弹性位移比谱表达式。Hatzigeorgiou[4]对单自由度体系在近断层和远场地震动作用下的延性需求谱进行了比较分析，建立了以周期、阻尼比、刚度比以及力减小因子作为基本参数的延性需求谱的数学表达式。Iervolino等[5]在大量近断层脉冲型地震记录的基础上建立了等强度折减系数非弹性位移比谱的解析表达式。Garcia[6]对前向近断层地震动作用下退化和非退化单自由度体系的等强度折减系数非弹性位移比谱进行了研究，建立了非弹性位移比谱的数学表达式。韦承基[7]研究了弹塑性结构最大位移响应与弹性结构最大位移响应之间的关系，建立了可用于结构抗震设计的弹性位移需求谱及弹塑性位移比谱。肖明葵等[8]对采用双线性恢复力模型的弹塑性单自由度体系的位移比谱进行了研究，通过数值拟合方法建立了弹塑性位移比谱的数学表达式。夏洪流等[9]以非线性单自由度体系为研究对象，研究了结构位移响应最大值与结构基本周期、屈服强度系数以及屈服后刚度系数间的关系，建立了最大位移响应的估算公式。黄建文等[10]建立了理想弹塑性结构的等延性非弹性位移比谱，研究了刚度退化、强度退化以及捏拢效应等退化因素对非弹性位移比谱的影响。翟长海等[11]研究了场地条件、屈服强度、自振周期以及恢复力模型等因素对等强度位移比谱的影响规律，建立了等强度位移比谱的数学表达式。徐福江等[12]研究了滞回模型、阻尼比以及屈服后刚度系数对等延性位移需求谱的影响，通过数值拟合方法建立了等延性位移需求谱的数学表达式。

综上所述，已有研究主要针对传统抗震结构的非弹性位移需求谱进行研究，研究中所用恢复力模型、参数的定义和取值等均以传统抗震结构为准。近年来，随着隔震技术在实际工程中的大量应用，围绕隔震结构开展的研究呈多元化发展趋势，其中，易伟建等[13～16]对隔震结构的弹性位移需求谱进行了研究，而关于隔震结构非弹性位移需求谱方面的研究则相对较少。文中以对隔震结构影响显著的近断层脉冲型地震记录作为激励，采用Bouc-Wen模型描述隔震支座的非线性力-变形关系，建立隔震结构非弹性位移需求谱的基本方程，运用Matlab求解得到了隔震结构的等强度位移需求谱，并给出了其数学表达式。

1 运动方程的建立

地震作用下，非弹性单自由度体系的运动方程为

(1)

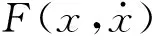
(2)

式中:α代表体系屈服后与屈服前刚度比；k代表体系屈服前刚度；xy代表体系屈服位移；Z代表体系的滞变分量，具体表达式为

(3)

将式(2)代入式(1)，并与式(3)一起组成方程组

(4)

对该微分方程组进行求解可以得到非弹性单自由度体系在地震作用下的位移响应、速度响应和加速度响应。

2 等强度位移需求谱的基本方程

将式(4)两边同除以m，得到建立非弹性位移需求谱的基本方程

(5)

更进一步，如果以圆频率作为自变量，给定其它变量值，通过求解便可以得到圆频率与体系位移响应最大值之间的对应关系，从而建立体系的非弹性位移需求谱。为了建立等强度位移需求谱，先对强度折减系数Ry进行定义，其表达式为

Ry=mSa/fy

(6)

式中:m为体系的质量；Sa为弹性单自由度体系的谱加速度，与非弹性单自由度体系对应；fy为体系的屈服强度;mSa为体系在地震作用下保持弹性所需的最小强度。

将式(5)左右两边同除以xy，引入变量u=x/xy和Ry，通过对方程组进行变形得到以强度折减系数Ry作为参变量的方程组

(7)

以强度折减系数Ry作为参变量，对式(7)进行求解，并对求解结果进行处理，便可以建立体系的等强度位移需求谱。

3 等强度位移需求谱的建立

根据隔震结构的力学特性，在建立隔震结构的等强度位移需求谱时，周期T的取值范围取0.1～6 s，间隔0.1 s，上部结构阻尼比ζ取0.05，支座屈服后与屈服前刚度比α取0.1，用于描述隔震支座非线性行为的Bouc-Wen模型的相关参数β，γ，η，A的取值分别为0.5，0.5，1，1。将上述参数代入前文已经建立的运动方程，以36条脉冲型地震记录(详见文献[16]，研究者在该文献中已对脉冲型地震动的选取准则和选取结果进行了论述，不再赘述)作为输入，求解并建立隔震结构的等强度位移需求谱。

图1(a)和(b)所示为强度折减系数分别取5和6时建立的等强度非弹性位移谱。从图中可以看出，不同脉冲型地震记录作用下等强度位移需求谱的差别很大，谱峰值及其在横坐标轴上的投影值(周期)分布范围很广。

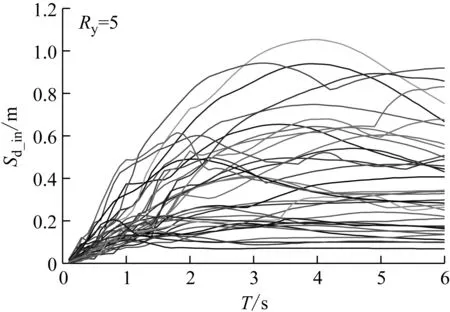
(a) Ry=5

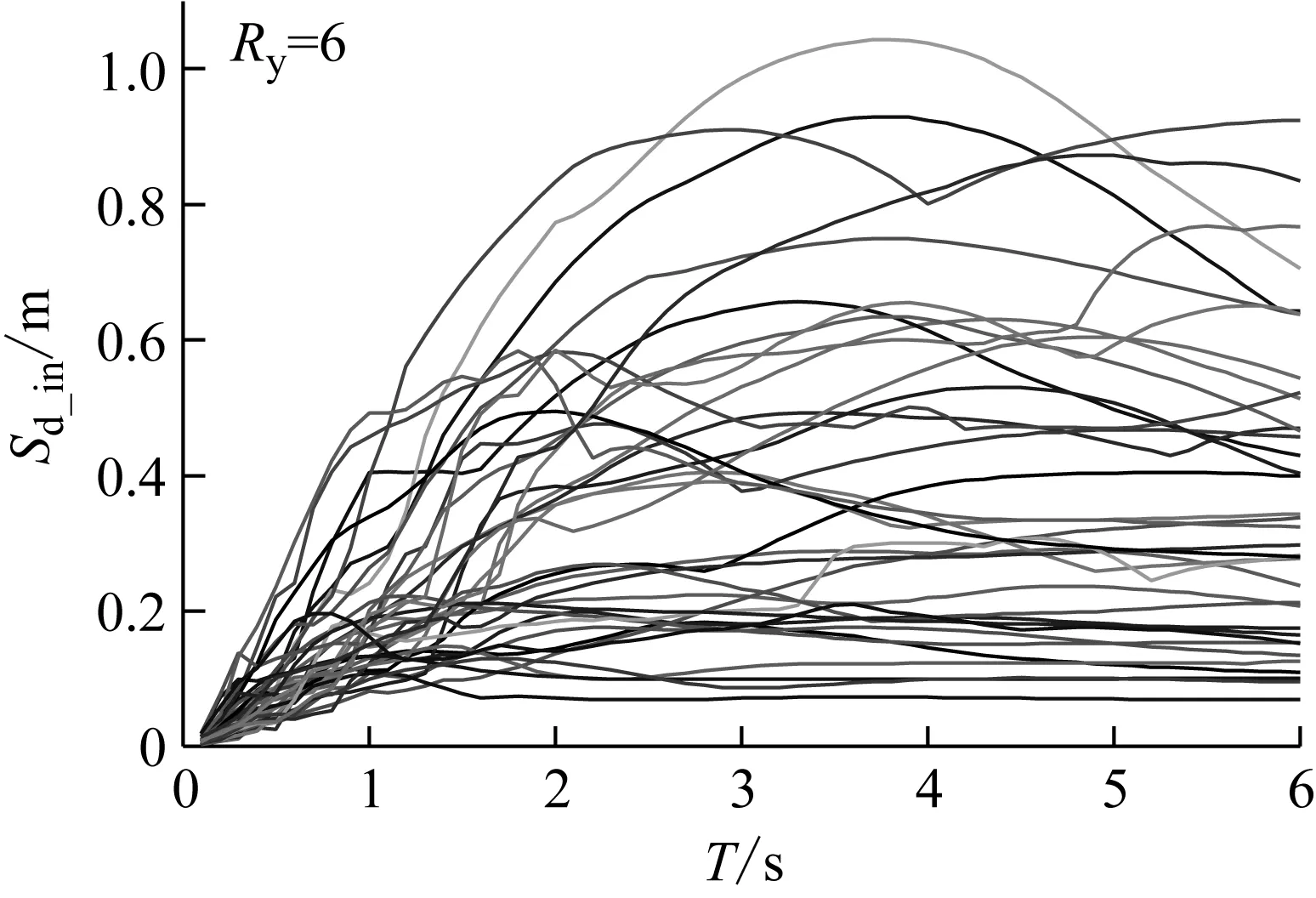
(b) Ry=6

图2(a)和(b)所示为强度折减系数分别取5和6时建立的标准化等强度位移需求谱。从图中可以看出，与原始等强度位移需求谱相比，经标准化后等强度位移需求谱的特征非常明显，如：谱形相似，均包括上升段、下降段、平稳段和水平段四个阶段；均存在明显的谱峰值。但是，谱峰值的变化幅度较大，且强度折减系数对谱峰值存在一定的影响。

图3(a)和(b)所示分别为强度折减系数Ry对平均等强度位移需求谱和单个等强度位移需求谱的影响。从图中可以看出，在等强度位移需求谱中存在一个临界周期，当体系周期小于该临界周期时，位移谱的谱值随强度折减系数的增大呈增大趋势；当体系周期大于该临界周期时，位移谱的谱值随强度折减系数的增大呈减小趋势。另外，强度折减系数在整个周期段对位移谱谱值的影响都较为明显。

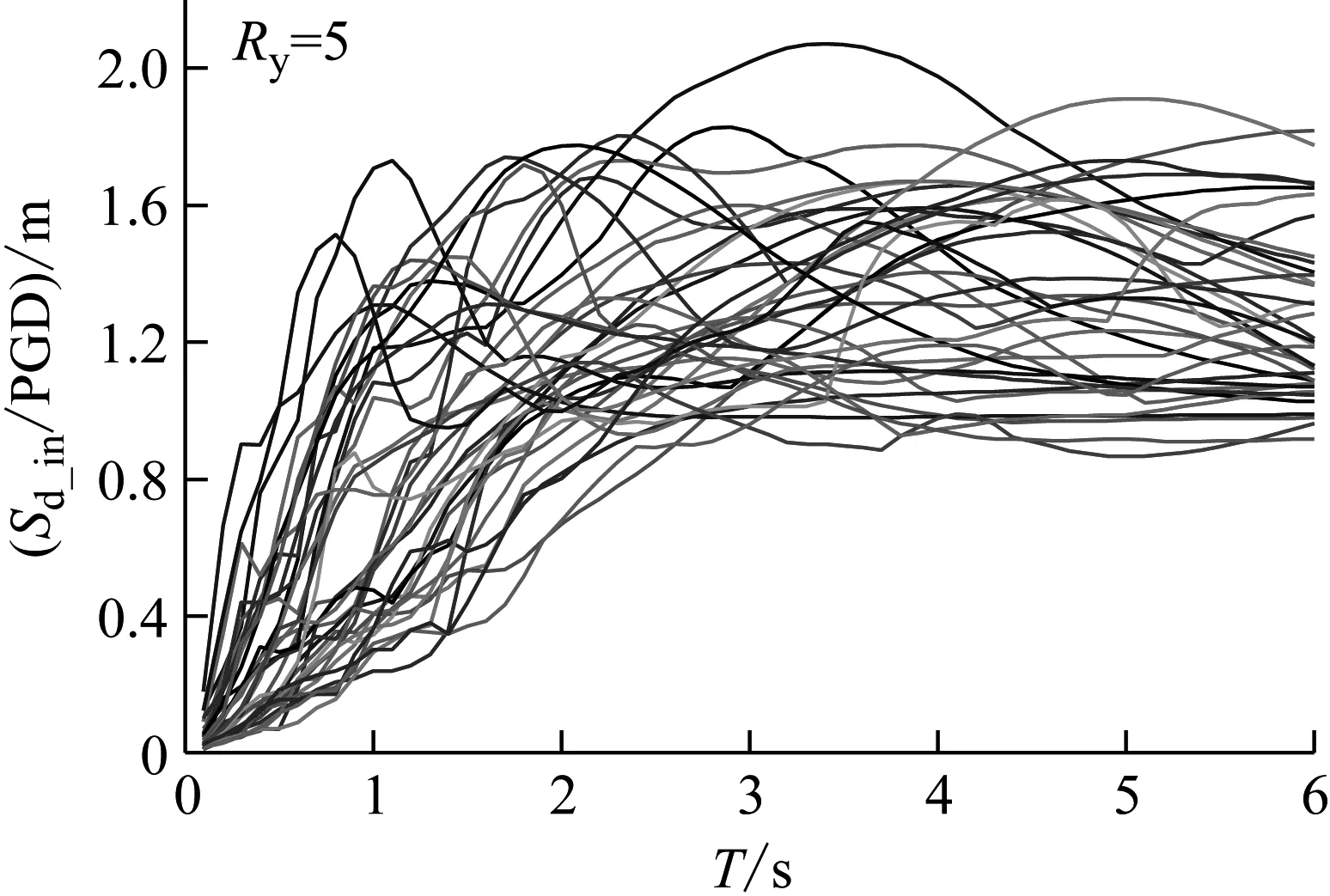
(a) Ry=5

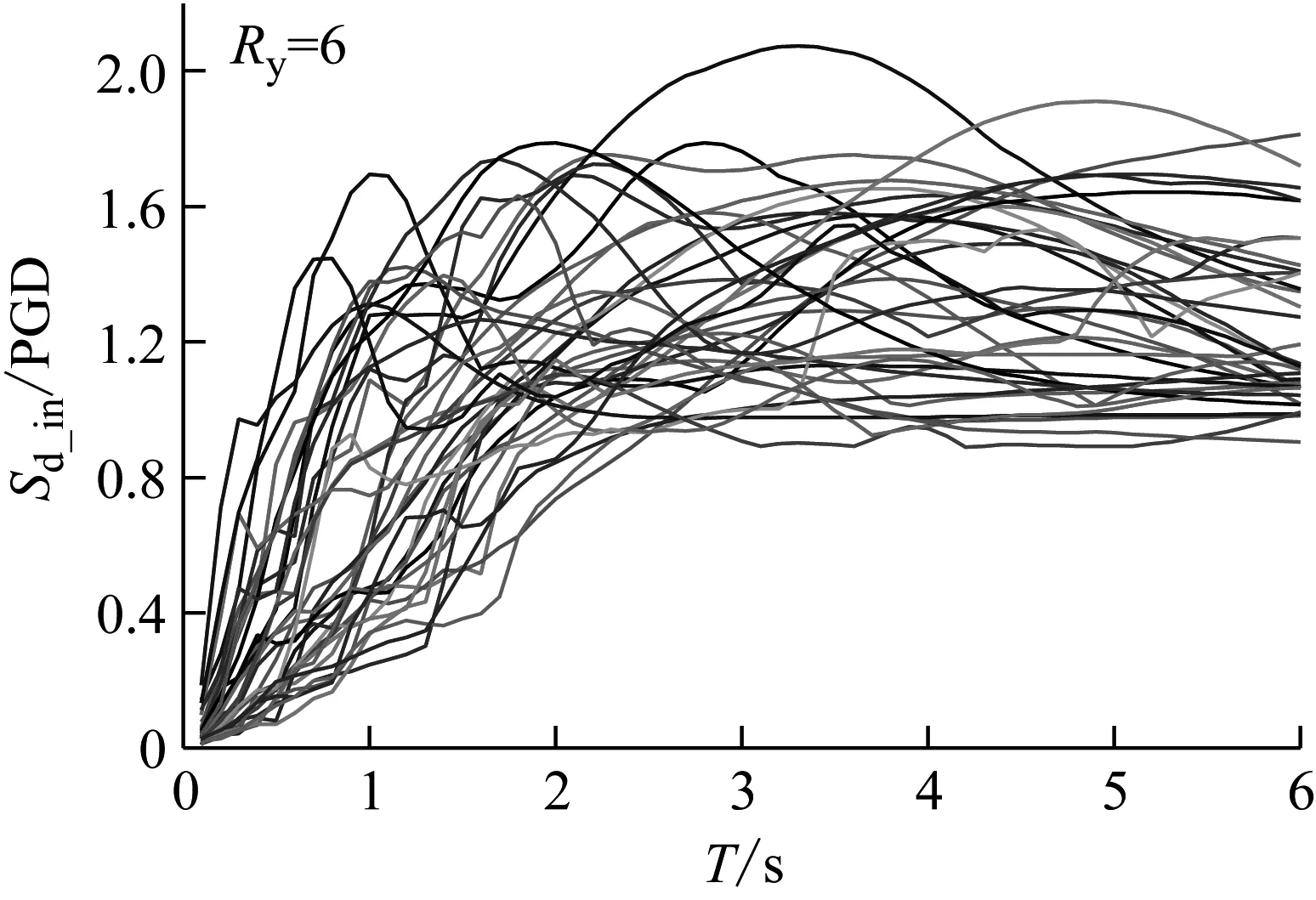
(b) Ry=6

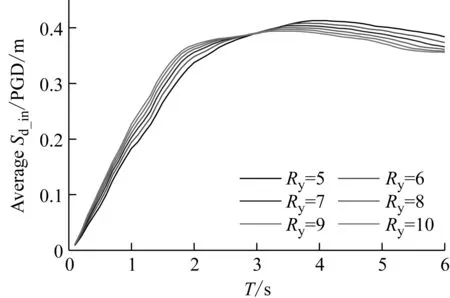
(a) 平均等强度位移需求谱

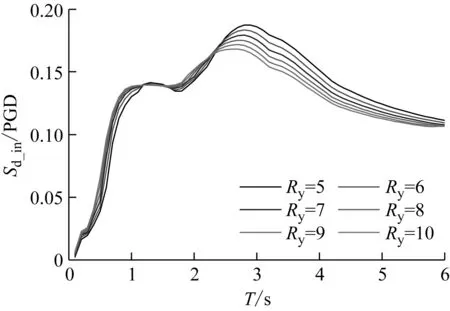
(b) 单条等强度位移需求谱

Fig.3 Influence of strength reduction factor on constant-strength displacement demand spectra

4 等强度位移需求谱的数学表达式

图4(a)和(b)所示为强度折减系数分别取5和6时建立的等强度位移比谱，图中细实线为各地震动作用下的等强度位移比谱，粗实线为平均等强位移比谱。从图中可以看出，在短周期段，等强度位移比谱的波动幅度很大，经平均后呈陡降趋势；在中长周期段，等强度位移比谱的波动幅度较大，经平均后呈平稳下降趋势；在长周期段，等强度位移比谱的波动幅度很小，基本在“1”附近波动。

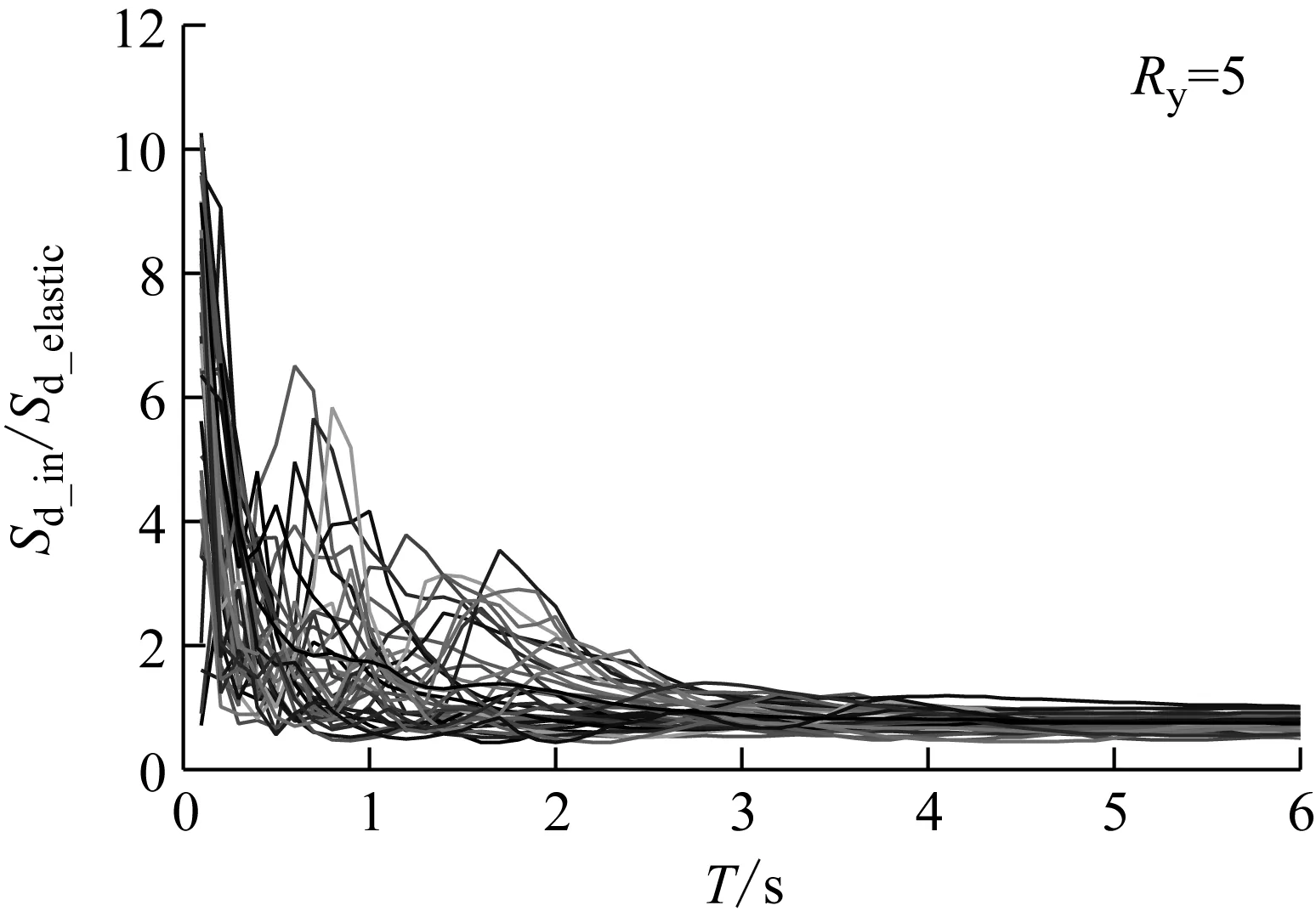
(a) 强度折减系数为5

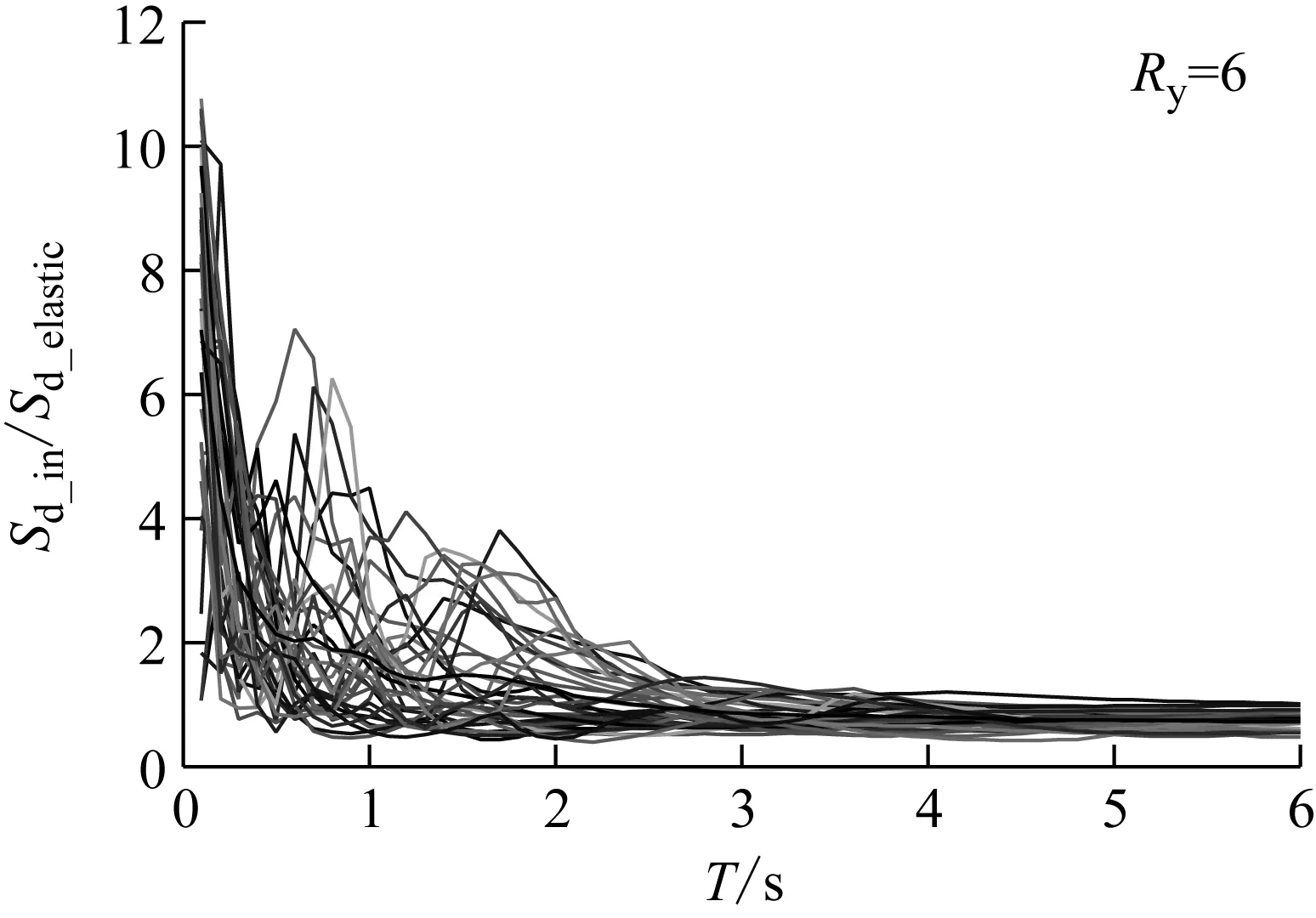
(b) 强度折减系数为6

图5(a)和(b)所示分别为强度折减系数对平均等强度位移比谱和单个等强度位移比谱的影响。从图中可以看出，在等强度位移比谱中存在一个临界周期，当体系周期小于该临界周期时，位移比谱值随着强度折减系数的增大呈增大趋势；当体系周期大于该临界周期时，位移比谱值随着强度折减系数的增大呈减小趋势。另外，强度折减系数对位移比谱值的影响在短周期段和中长周期段较为明显，在长周期段不明显。

通过非线性曲线拟合方法得到了等强度位移比谱的数学表达式，运用该表达式可以直接在弹性位移需求谱的基础上获得等强度位移需求谱，便于在实际工程进行应用，具体表达式为

RDis(T)=aTb+cT+d

(8)

式中:T为体系的自振周期;a,b,c和d为表达式的相关参数，它们的取值与强度折减系数的取值大小有关，见表1。

运用式(8)即可在弹性位移需求谱Sd_el的基础上，得到等强度非弹性位移需求谱Sd_in，具体表达式如下

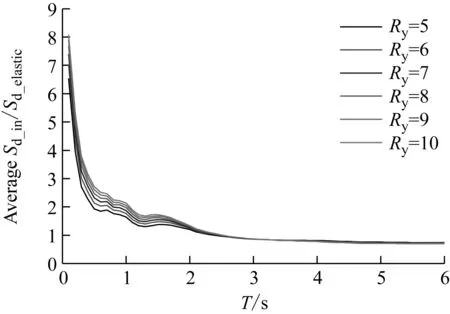
(a) 平均等强度位移比谱

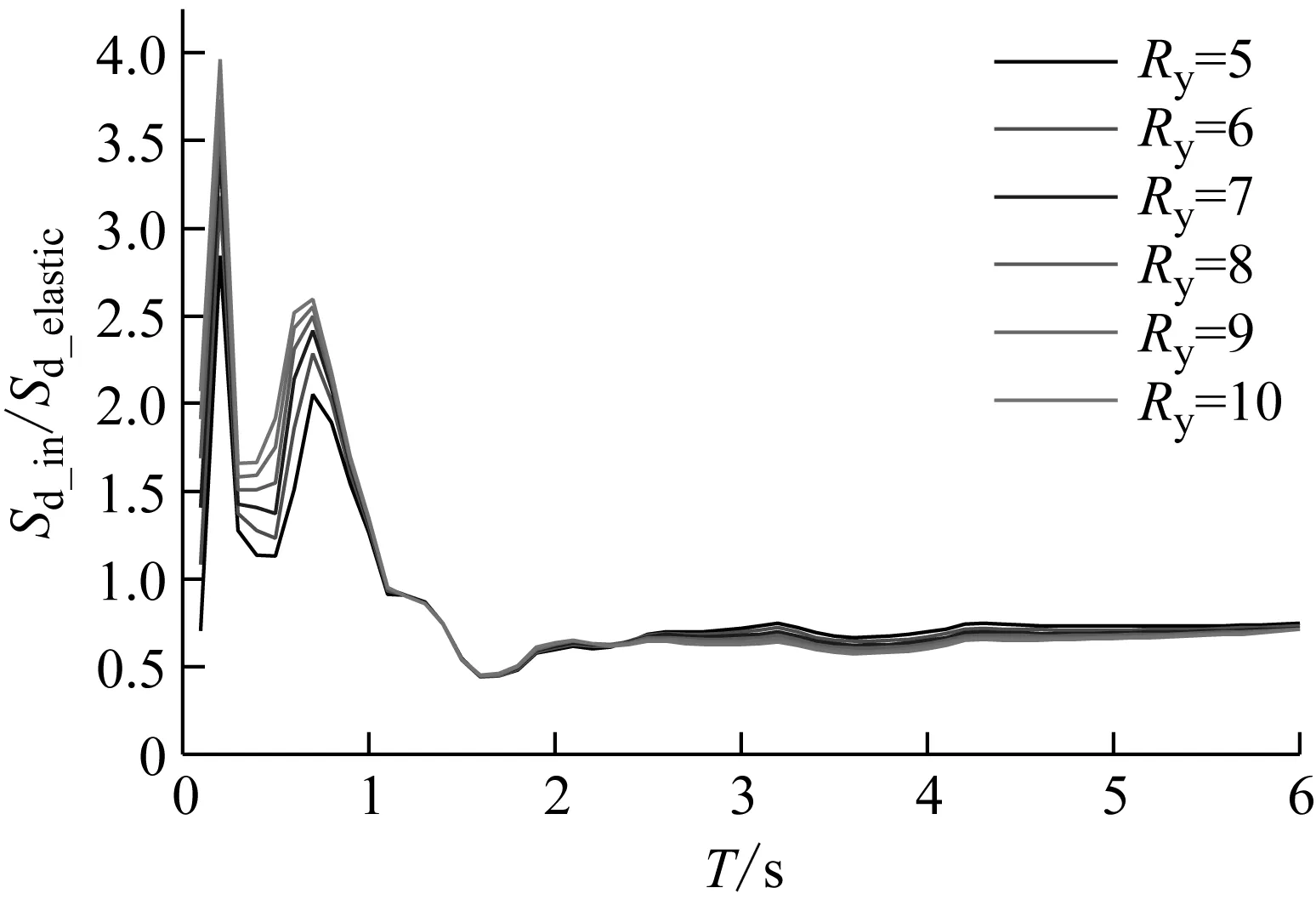
(b) 单条等强度位移比谱

Fig.5 Influence of strength reduction factor on constant-strength displacement ratio spectra

表1等强度位移比谱表达式的参数取值

Tab.1Parametervaluesofconstant-strengthdisplacementratiospectra

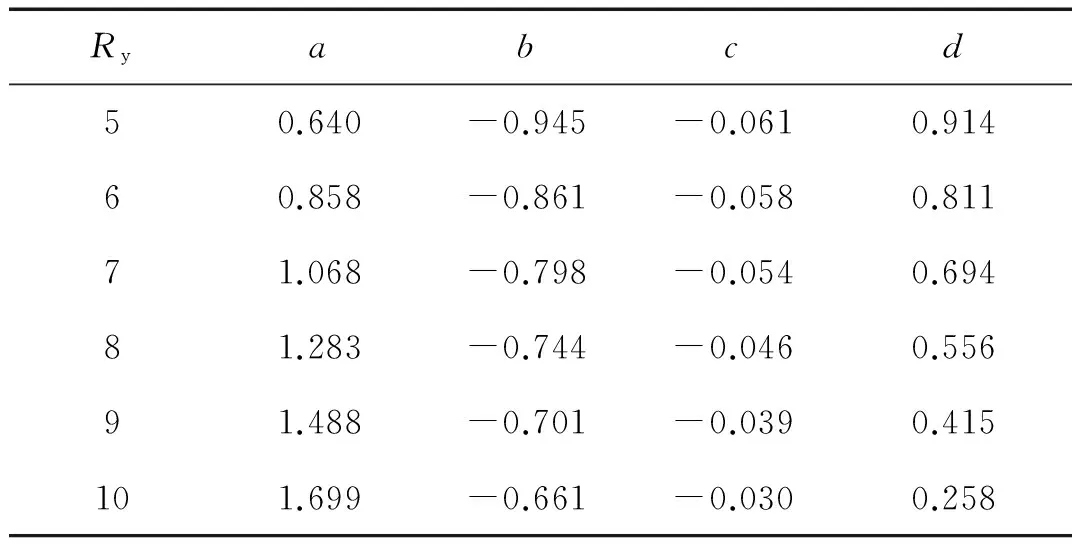
Ryabcd50.640-0.945-0.0610.91460.858-0.861-0.0580.81171.068-0.798-0.0540.69481.283-0.744-0.0460.55691.488-0.701-0.0390.415101.699-0.661-0.0300.258

Sd_in=RDis·Sd_el

(9)

图6(a)和(b)所示为强度折减系数分别取5和6时，真实非弹性位移比谱和拟合非弹性位移比谱之间的对比。从图中可以看出，拟合非弹性位移比谱与真实非弹性位移比谱之间的匹配度很高，表明文中给出的拟合表达式具有一定的准确性。另外，表1列出了拟合表达式中相关参数的取值，便于实际工程应用。

5 结 论

为了对隔震支座的地震位移需求进行快速、高效估算，文中对脉冲型地震动作用下基础隔震结构的等强度位移需求谱进行了研究，研究结果如下：

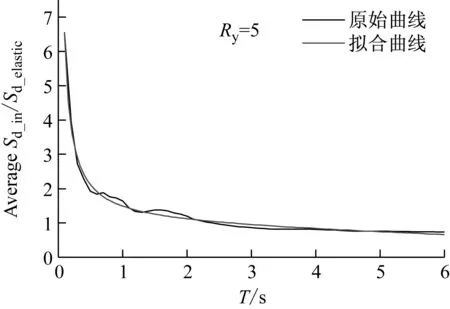
(a) Ry=5

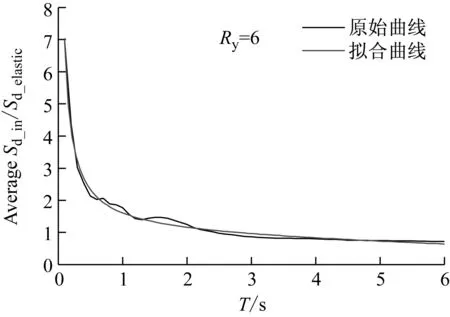
(b) Ry=6

Fig.6 Comparison between realistic and fitting constant-strength displacement ratio spectra

(1) 存在一临界周期，位移需求谱的谱值在该周期两侧随强度折减系数的变化规律截然相反。

(2) 与短周期及中长周期段相比，等强度位移比谱在长周期段围绕“1”小幅波动，受强度折减系数的影响较小。

(3) 给出了等强度位移需求谱的数学表达式，便于隔震支座非弹性位移需求的快速估算。

[1] 王亚楠, 李慧, 杜永峰. TMD-基础隔震混合控制体系在近场地震作用下的能量响应与减震效果分析[J]. 振动与冲击, 2014, 33(4): 204-209.

WANG Yanan, LI Hui, DU Yongfeng. Energy response and anti-vibration effect analysis for a base-isolated structure with TMD under near-field earthquake[J]. Journal of Vibration and Shock, 2014, 33(4): 204-209.

[2] BORZI B, CALVI G M, ELNASHAI A S. Inelastic spectra for displacement-based seismic design[J]. Soil Dynamic and Earthquake Engineering, 2001, 21(5): 47-61.

[3] CHOPRA A K, CHINTANAPAKDEE C. Inelastic deformation ratios for design and evaluation of structures: single degree of freedom bilinear systems[J]. Journal of Structural Engineering, 2004, 28(5): 1309-1319.

[4] HATZIGEORGIOU G D. Ductility demand spectra for multiple near and far fault earthquakes[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(2): 170-183.

[5] IERVOLINO I, CHIOCCARELLI E, BALTZOPOULOS G. Inelastic displacement ratio of near source pulse like ground motions[J]. Earthquake Engineering and Structural Dynamics, 2012, 41(3): 2351-2357.

[6] GARCIA J R. Inelastic displacement ratios for seismic assessment of structures subjected to forward-directivity near-fault ground motions[J]. Journal of Earthquake Engineering, 2011, 15(5): 449-468.

[7] 韦承基. 弹塑性结构的位移比谱[J]. 建筑结构, 1997, 20(3): 40-48.

WEI Chengji. Displacement ration spectrum of elasto-plastic structures[J].Journal of Building Structures,1997,20(3):40-48.

[8] 肖明葵, 王耀伟, 严涛,等. 抗震结构的弹塑性位移需求谱[J]. 重庆建筑大学学报, 2000, 22(增刊1): 34-40.

XIAO Mingkui, WANG Yaowei, YAN Tao, et al.The spectrum of elasto-plastic displacement for seismic structures[J].Journal of Chongqing Jianzhu University,2000,22(Sup1): 34-40.

[9] 夏洪流, 李英民, 杨溥. 罕遇地震作用下SDOF结构位移响应的统计特性分析[J]. 重庆建筑大学学报, 2000, 22(增刊1): 139-143.

XIA Hongliu, LI Yingmin, YANG Pu, et al. Analysis of the statistic characteristics of displacement response of SDOF system under rare earthquake[J]. Journal of Chongqing Jian-zhu University, 2000,22(Sup1):139-143.

[10] 黄建文, 朱晞. 近震作用下单自由度结构的非弹性响应分析研究[J]. 中国安全科学学报, 2003, 13(11): 59-65.

HUANG Jianwen, ZHU Xi. Inelastic response analysis for the SDOF structures under near-field earthquake[J]. China Safety Science Journal,2003,13(11):59-65.

[11] 翟长海, 李爽, 谢礼立,等. 近场脉冲型地震动位移比谱特征研究[J]. 土木工程学报, 2008, 41(10): 1-5.

ZHAI Changhai, LI shuang, XIE Lili, et al. Charac-teristics of displacement ratio spectra for near-field motions[J].China Civil Engineering Journal, 2008, 41(10): 1-5.

[12] 徐福江, 钱稼茹. 常延性系数弹塑性位移需求谱及其应用[J].工程力学, 2007, 24(6): 15-20.

XU Fujiang, QIAN Jiaru. Costant ductility inelastic displacement spectrum and its application[J]. Engineering Mechanics, 2007, 24(6): 15-20.

[13] 易伟建, 张海燕. 弹塑性反应谱的比较及其应用[J].湖南大学学报(自然科学版), 2005, 32(2): 42-45.

YI Weijian, ZHANG Haiyan. Comparison and application of elastic-plastic response spectra[J]. Journal of Hunan University(Natural Science), 2005, 32(2): 42-45.

[14] 翟长海, 李爽, 谢礼立. 抗震结构非弹性位移比谱[J]. 哈尔滨工业大学学报, 2009, 41(2): 1-4.

ZHAI Changhai, LI Shuang, XIE Lili, et al. Inelastic displacement ratio spectra of seismic structures[J]. Journal of Harbin Instiute of Technology, 2009, 41(2): 1-4.

[15] 翟长海, 公茂盛, 谢礼立. 工程结构等强度位移比谱影响因素分析[J]. 哈尔滨工业大学学报, 2005, 37(4): 455-458.

ZHAI Changhai, GONG Maosheng, XIE Lili, et al. Influence analysis on displacement ratio spectra of constant yielding strength for evaluation of existing structures[J]. Journal of Harbin Instiute of Technology, 2005, 37(4): 455-458.

[16] 王亚楠, 李慧, 杜永峰, 等. 近场脉冲型地震动作用下设计位移反应谱[J]. 中南大学学报(自然科学版), 2015, 46(4): 1511-1517.

WANG Yanan, LI Hui, DU Yongfeng, et al. Displacement design spectra for near-fault pulse-type ground motions[J]. Journal of Central South University(Science and Technology), 2015, 46(4): 1511-1517.