基于模态测试的宽幅钢箱梁桥有限元模型建立、修正与分析
2018-02-27谢伟平曹晓宇肖伯强刘海庆
谢伟平, 曹晓宇, 肖伯强, 刘海庆
(1.武汉理工大学 土木工程与建筑学院,武汉 430070; 2.中交第二航务工程局有限公司第六工程分公司,武汉 430070)
为了解决城市交通日益拥挤的问题,城市高架桥桥梁宽度不断增大,同时受到下部行车空间与视野的限制,高架桥普遍采用中心支撑形式,此外在跨越交叉路口、河流湖泊时采用钢材质箱型截面以获得较大的跨越能力、较小截面高度和较短的施工周期。综上,此类钢箱梁桥具有宽跨比大、中心支撑、自重相对较轻等特征。
对于此类桥梁:一方面,由于宽跨比大且中心支撑,桥梁将表现出显著的空间效应,扭转模态对桥梁竖向动力响应的贡献将显著增大,此时传统桥梁模型(单梁[1]、梁格模型[2-3]、梁段元[4-5]等)将难以准确模拟其空间模态与考虑其剪力滞效应,此外采用单一的冲击系数衡量车辆的冲击系数显然也不再适用。另一方面,由于采用钢材质且跨度较大,此类桥梁具有结构轻柔、模态密集、阻尼比较小、自重相对较轻的特点,当重载卡车驶过时车桥耦合振动效应将十分显著且振动衰减较慢,由此带来的振动响应可能引起司乘人员的不舒适甚至恐慌心理。
目前,针对城市宽幅钢箱梁高架桥的施工、静力研究工作相对较多[6-7],广大学者也针对斜拉桥[8]、大跨度车站[9]、高层建筑[10]、大跨度刚构桥[11-12]、预应力混凝土简支梁桥[13-14]等开展了动力特性分析与实测工作,但是鲜见针对宽幅钢箱梁桥的动力特性的现场实测与分析工作。文献[15-16]仅建立了宽箱梁桥有限元模型,却缺乏实测数据验证。
本文首先针对宽幅钢箱梁桥的不同施工阶段开展基于环境激励作用下模态测试与分析工作,然后建立宽幅钢箱梁桥的精细三维有限元模型,并基于实测模态数据采用二阶响应面法对桥梁有限元模型进行修正,最后详细分析了桥梁铺装层、邻跨等效质量对桥梁自振频率的影响。
1 环境激励作用下桥梁模态测试与分析
1.1 工程概况
某在建高架桥为三跨连续钢箱梁桥(L7联),跨度58 m+89 m+58 m,桥面宽度33 m,双向八车道,悬臂端长度3.695 m,采用工厂分节段预制、现场拼装方式施工安装。上部结构为单箱六室封闭式箱型截面,顶板由下向上依次铺装8 cm厚钢纤维混凝土+9 cm厚沥青混凝土,下部采用H形双柱实体墩,墩高分别为9.894 m、8.491 m、9.081 m、11.106 m,墩柱中心间距8.5 m,墩身混凝土C40,采用低桩承台,尺寸10 m×8.5 m×3 m,桩基础采用钻孔灌注端承型,长度约50 m,桥梁两端采用SF320型伸缩缝,支座采用JQGZ万向球形支座。如图1和图2所示。
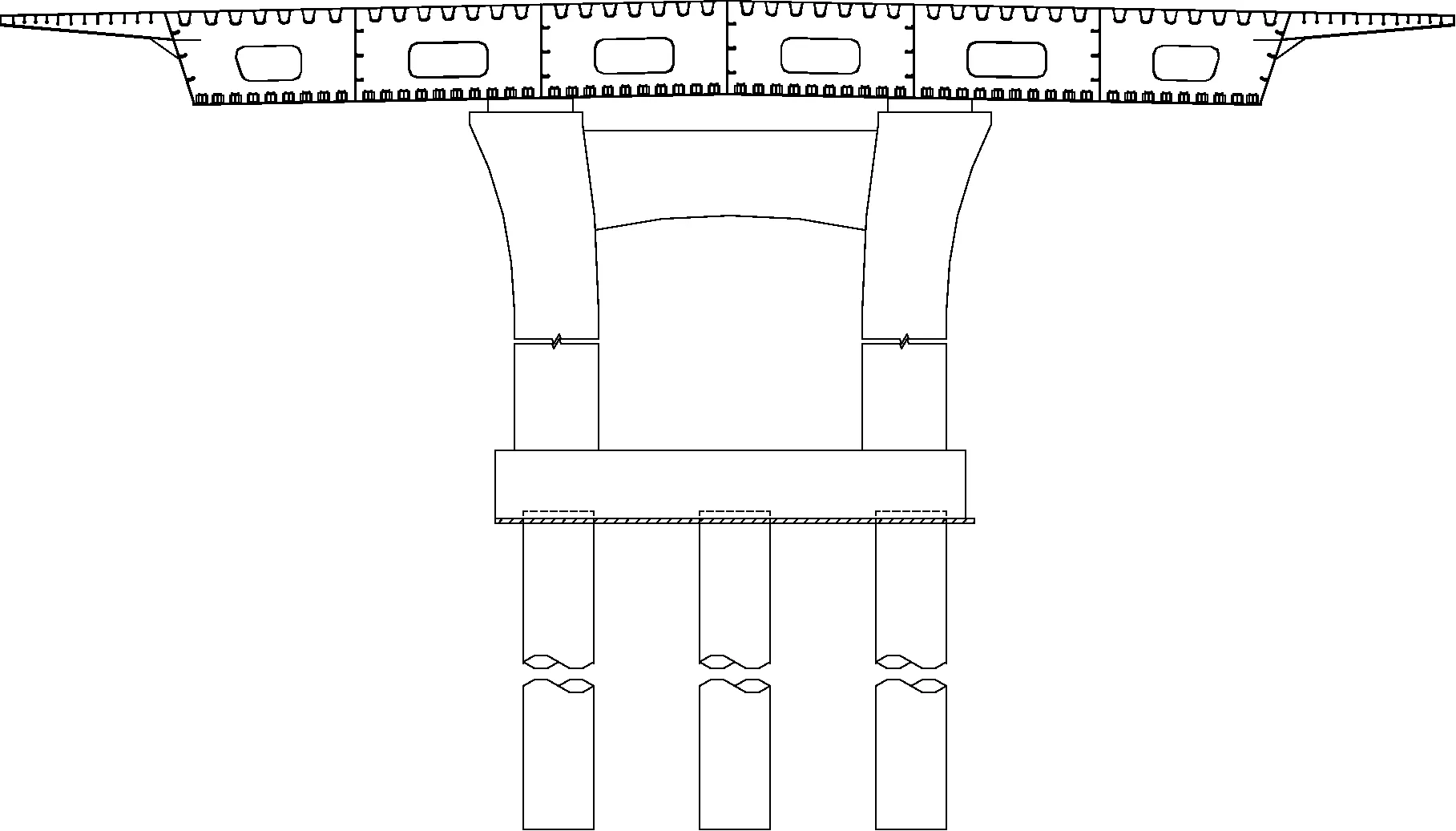
图1 桥梁支座处横截面示意图
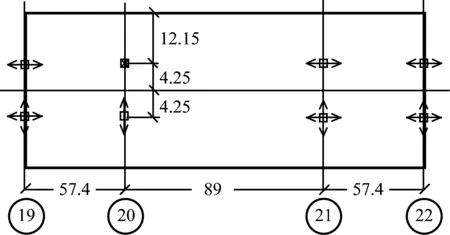
图2 支座平面布置示意图
1.2 模态测试工况及测点布置
针对桥梁的不同施工阶段共开展了3次模态测试,各次测试均采用相同的仪器与测点布置方案。第1次测试工况为下部结构完工,上部主梁完工,护栏安装完工且尚未铺装;第2次测试在第1次基础上,铺装8 cm厚钢钎维混凝土;第3次为全桥完工。
仪器为日本产SPC-51振动采集分析仪,VSE-15-D1伺服型速度传感器,传感器灵敏度:500 mv/(m/s2),频率范围:0.1~70 Hz,加速度量程:±20 m/s2。
从以上分析不难看出,经济是旅游的表象,文化是旅游的本质。从旅游发展史看出,各个时期的旅游活动都有其独特的表现形式及其不同的主题倾向,但在本质上具有一个共同之处,即旅游者在旅游活动中追求的是文化享受③。
所有测点均布置在下部有横隔板的桥面顶板上,测试时间不少于20 min,采样频率200 Hz,铅垂向、横向、纵向分别开展分组测试,具体测点布置见图3。
某组测试中参考点的三向加速度时程如图4和图5所示,从图中可以得出铅垂向加速度响应显著大于横向加速度响应,横向加速度响应大于纵向加速度响应。采用随机子空间法(SSI)与峰值拾取法(PPI)结合自编程序识别桥梁的模态,不同工况下识别的频率与阻尼见表1,见图6。
因工况1受施工干扰影响较大,导致仅有效识别出了结构前四阶竖弯模态与第一阶扭转模态。由表1知:①工况3相对于工况2结构前十二阶频率(第八阶除外)均显著减小,其中第一阶频率减幅达15.6%;②环境激励作用下结构第一阶阻尼比仅0.6%,对于此类大跨度钢结构进行弱振作用下动力分析时阻尼比取值应慎重选取;③对于此类桥梁结构,桥梁模态表现出频率低而密集、扭转模态多且靠前、横向弯曲与竖向扭转模态耦合等特点。
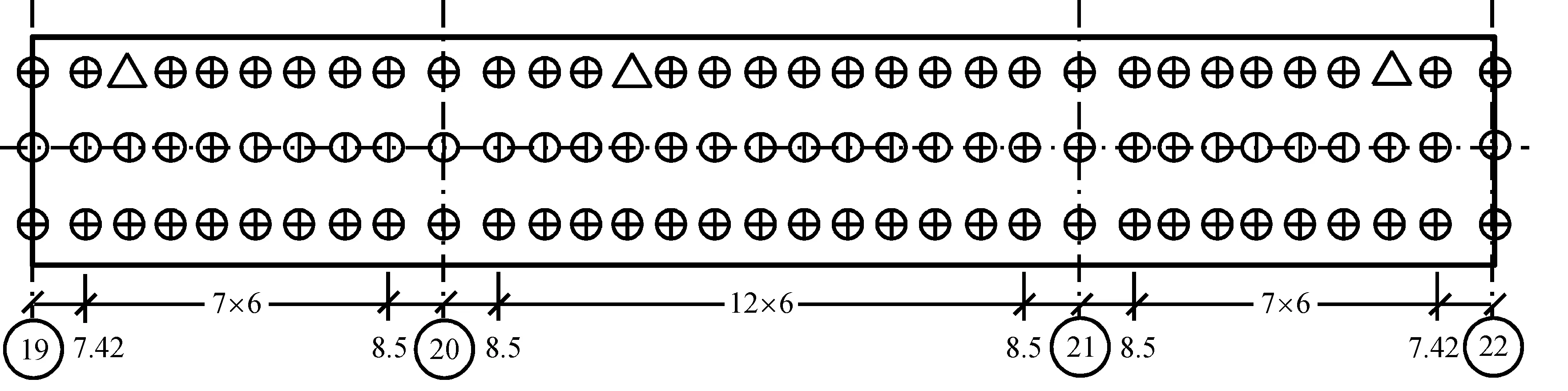

图3 测点布置图(m)
Fig.3 Arrangement of test point (m)
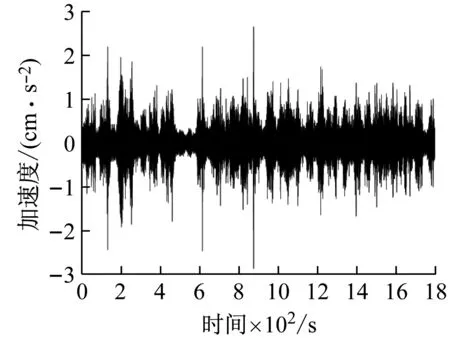
(a) 铅垂向
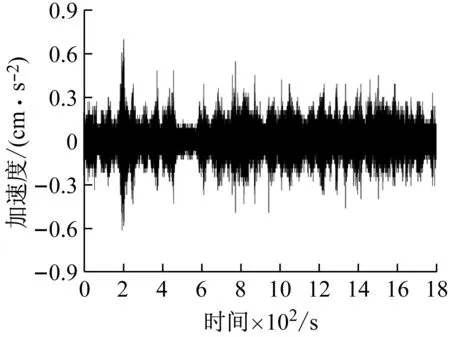
(b) 横向
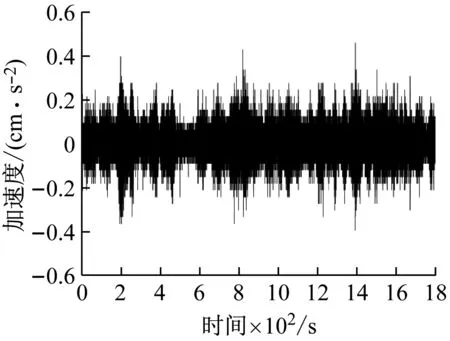
(c) 纵向

(a) 铅垂向参考点稳定图
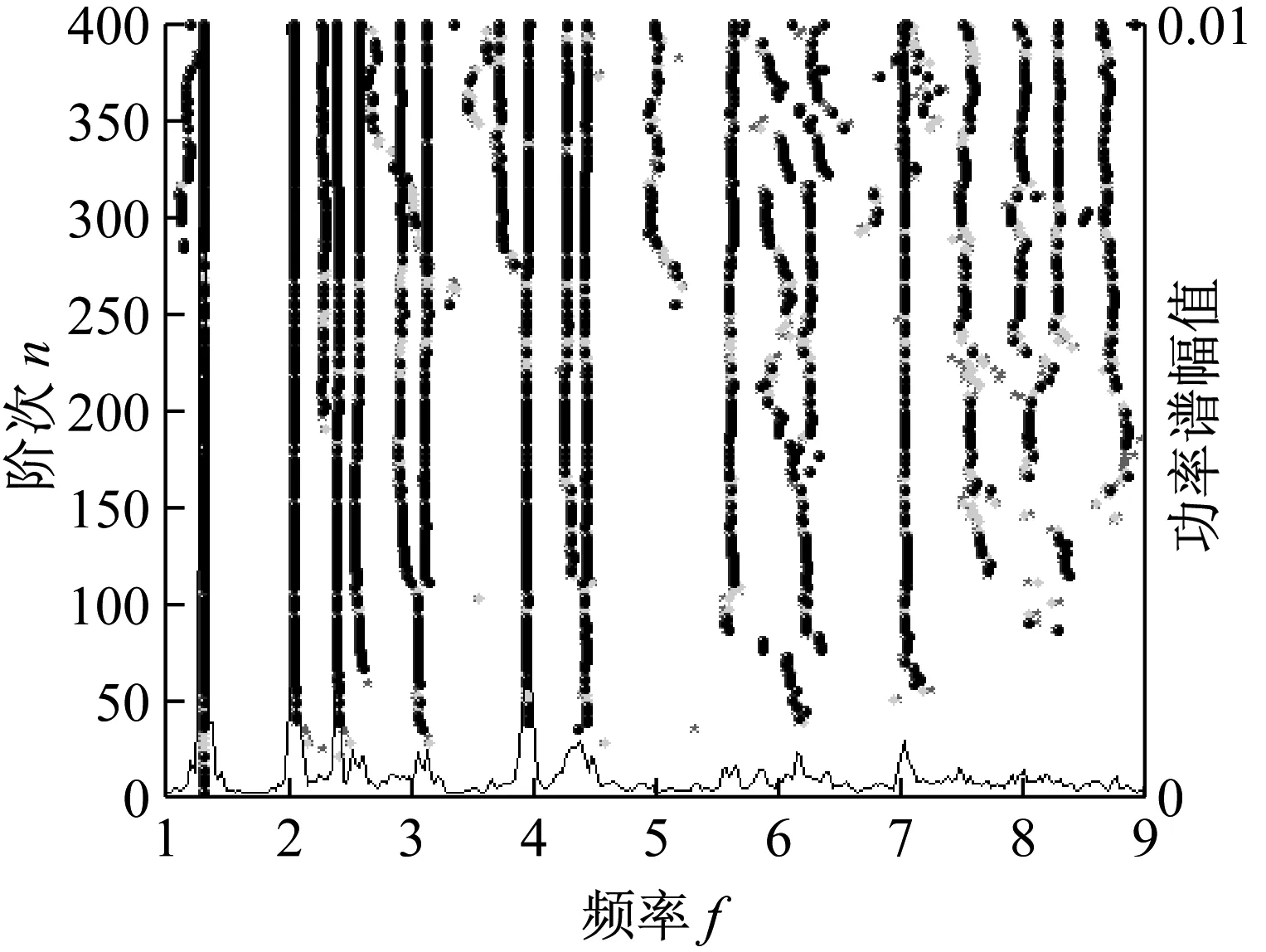
(b) 横向参考点稳定图
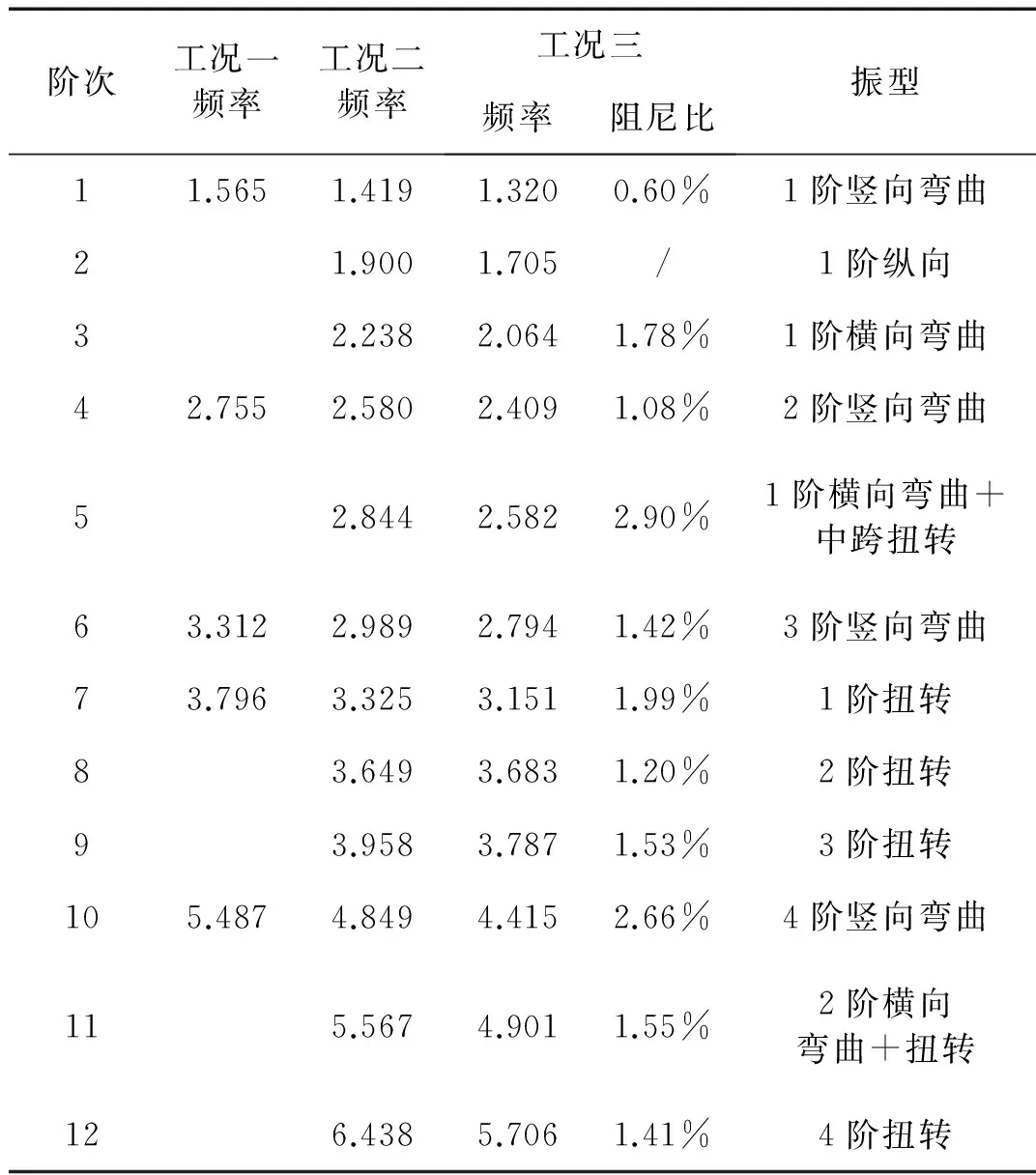
图5 参考点的稳定图
2 桥梁有限元模型建立
由于本文的桥梁结构为薄壁结构且宽跨比大,悬臂段较长,结构存在显著的剪力滞效应[17],考虑到ANSYS单元库提供了丰富有效的单元,可以较好地模拟薄壁结构的特点,故利用ANSYS采用不同的单元结合建立桥梁有限元模型。
对于桥梁各部分构件具体处理方式如下:
(1) 上部主梁,采用shell181单元模拟顶、底、腹板,beam188自定义截面模拟U、T、矩形加劲肋。
(2) 下部结构,采用solid65单元模拟桥墩与承台,beam188单元模拟群桩。
(4) 球形支座,采用6向弹簧单元combin14模拟,因无相关的支座刚度计算公式,且球形支座具有承载力大转动能力强的特点,据此将平动弹簧刚度(UX、UY、UZ)与转动刚度(ROTY、ROTZ)赋予较大的值,对ROTX赋予零值。
(5) 桩-土与承台-土相互作用,采用线性弹簧进行模拟,忽略土体质量与阻尼,具体刚度取值与计算公式根据规范[18]与文献[19]进行计算取值。
(6) 桥梁伸缩缝,采用纵向一维线性弹簧单元模拟,根据实测值调整弹簧刚度以接近实测值。
(7) 防撞护栏,对中防撞护栏采用beam188自定义梁截面模拟,边护栏采用beam188与shell181配合建模。
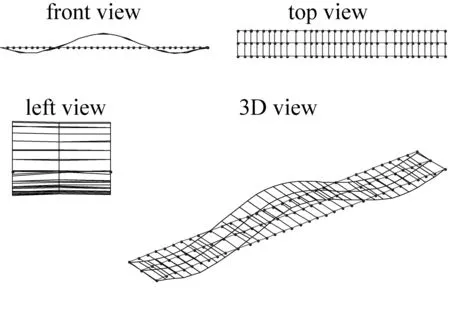
(a) 1阶竖向弯曲振型(1.320 Hz)
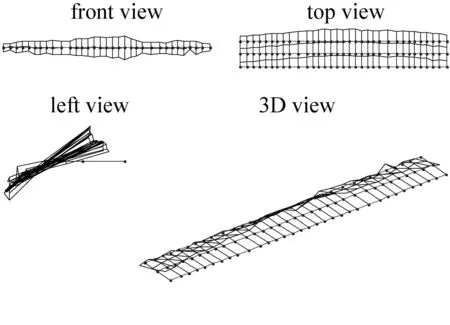
(b) 1阶横向弯曲振型(2.064 Hz)
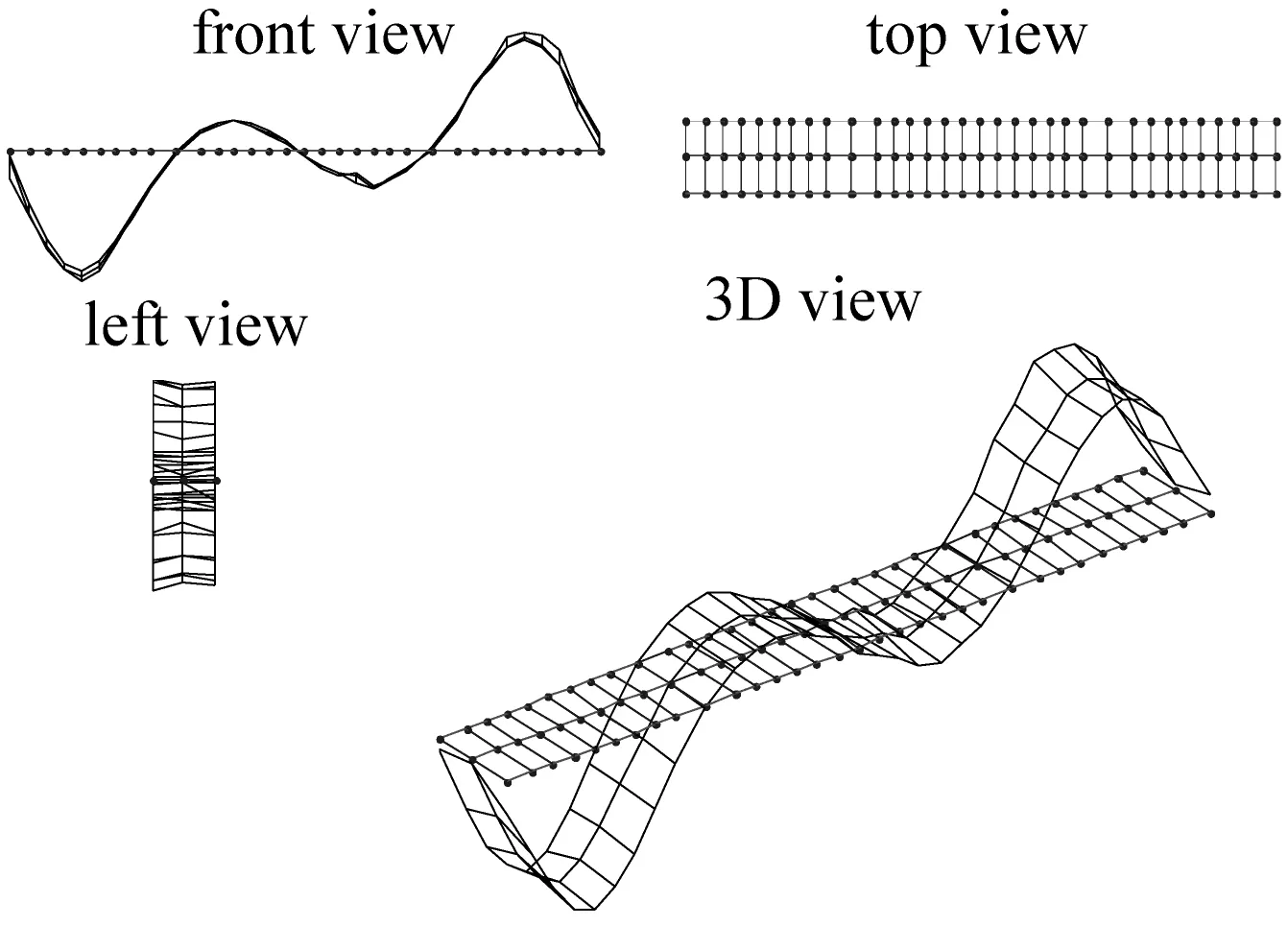
(c) 2阶竖向弯曲振型(2.409 Hz)
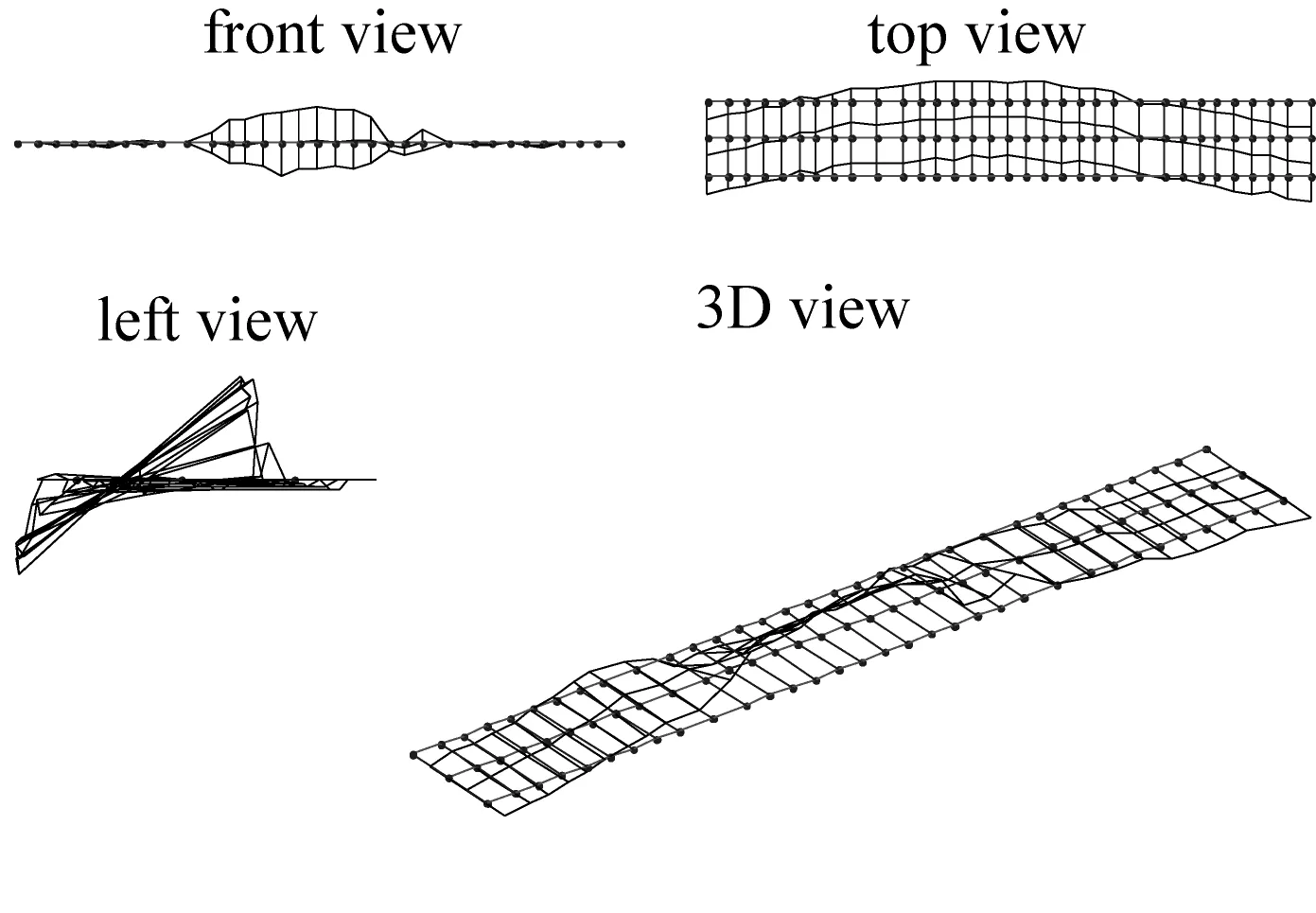
(d) 1阶横向弯曲+中跨扭转振型(2.582 Hz)
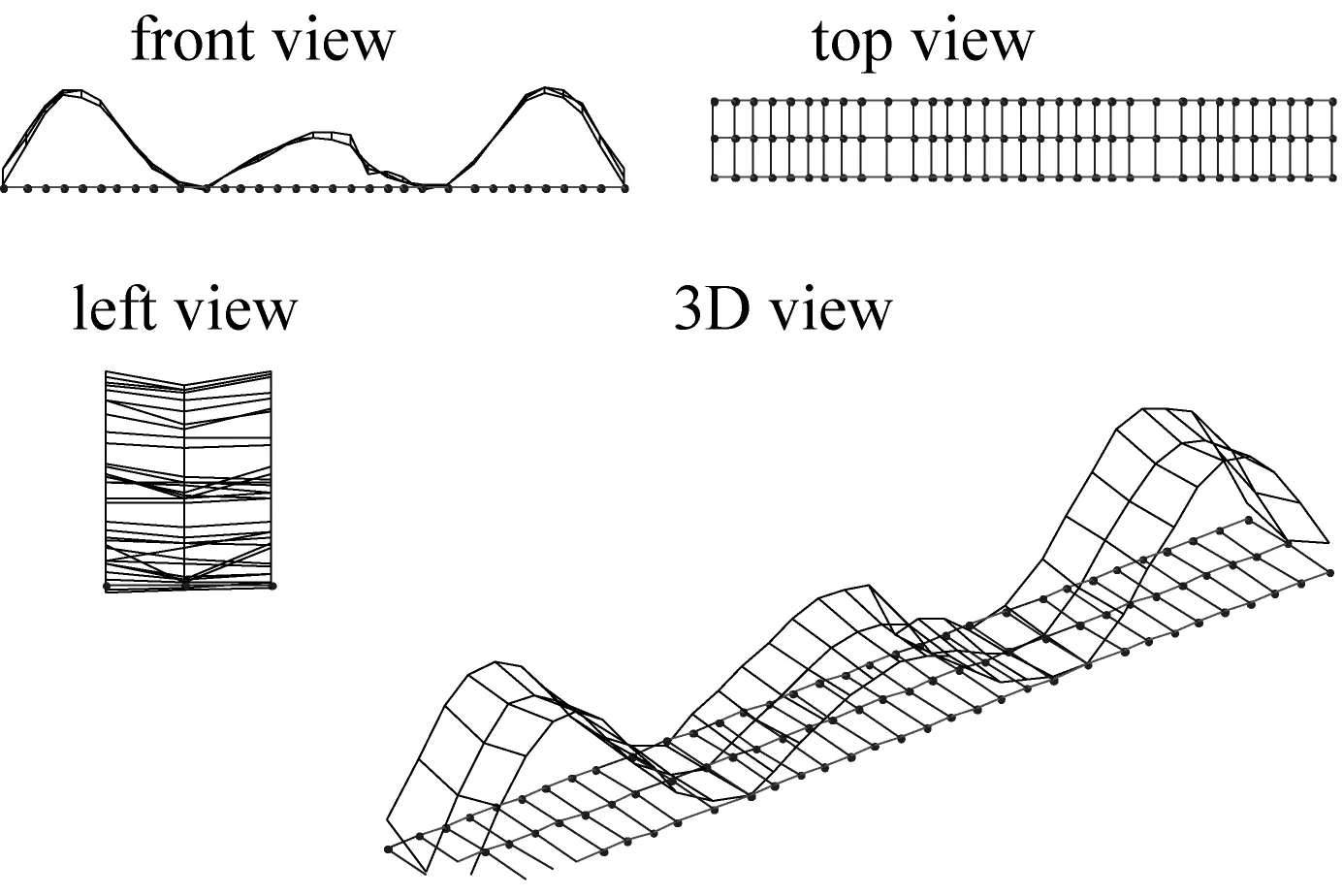
(e) 3阶竖向弯曲振型(2.794 Hz)
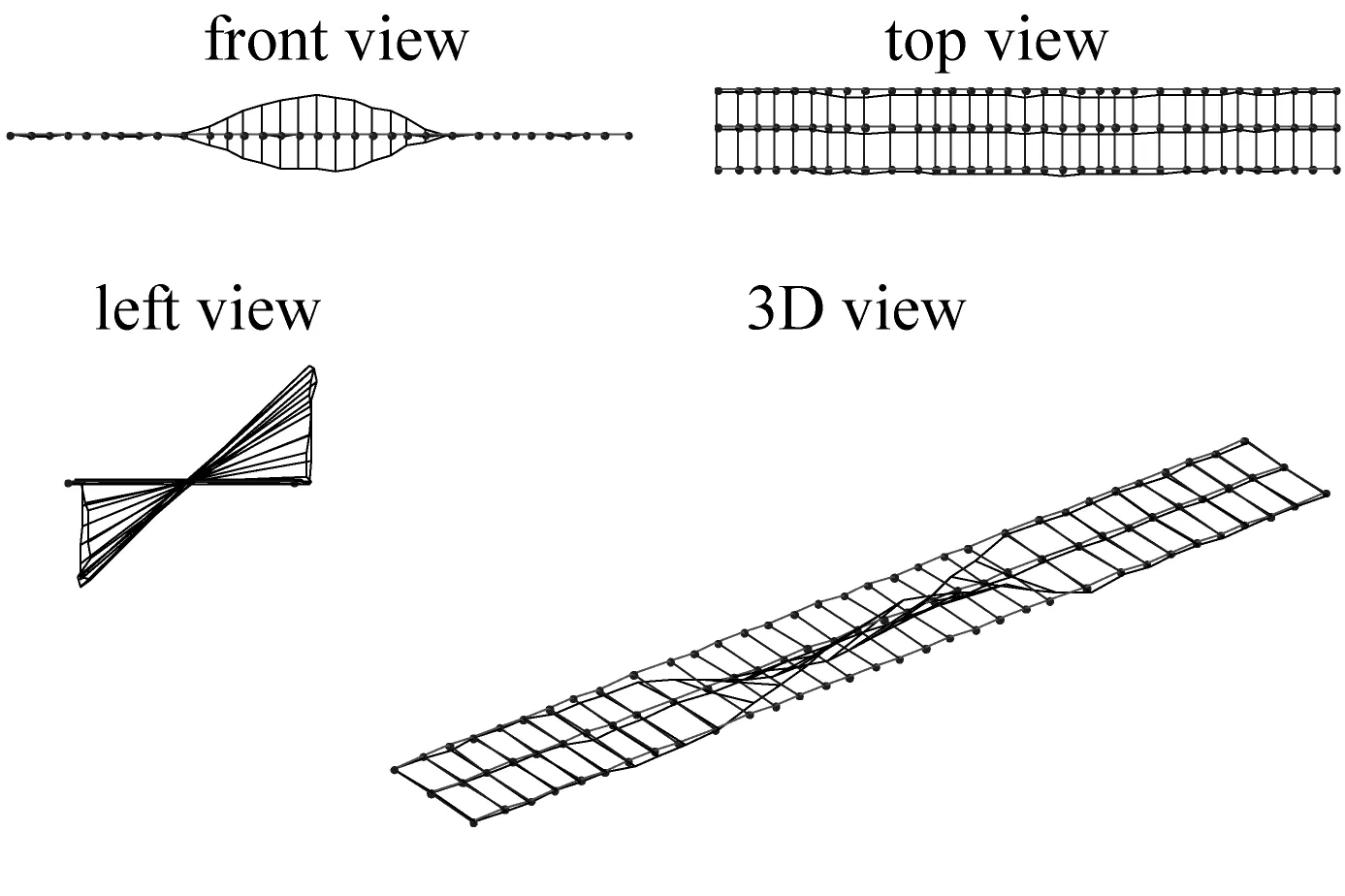
(f) 1阶扭转振型(3.151 Hz)
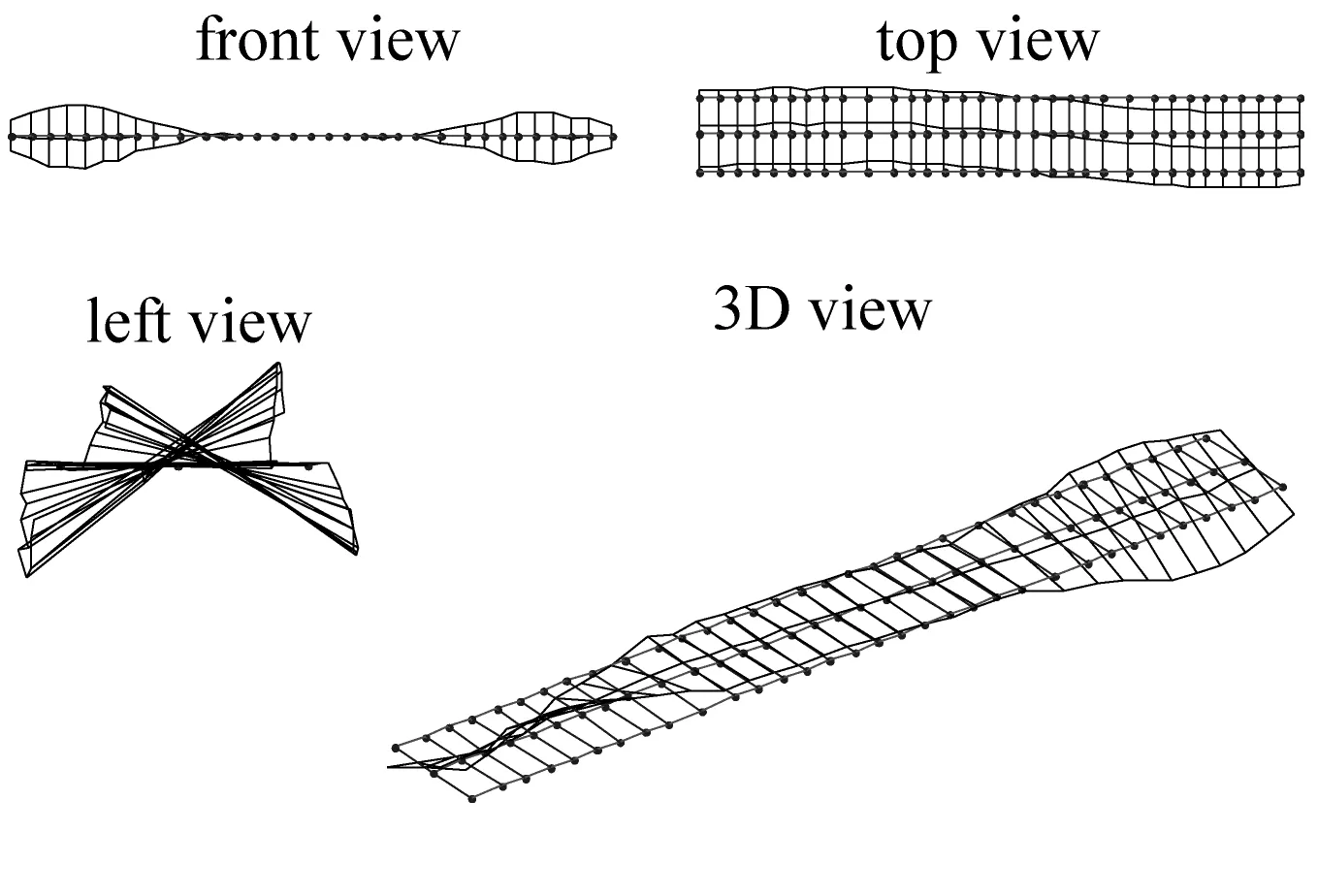
(g) 2阶扭转振型(3.683 Hz)
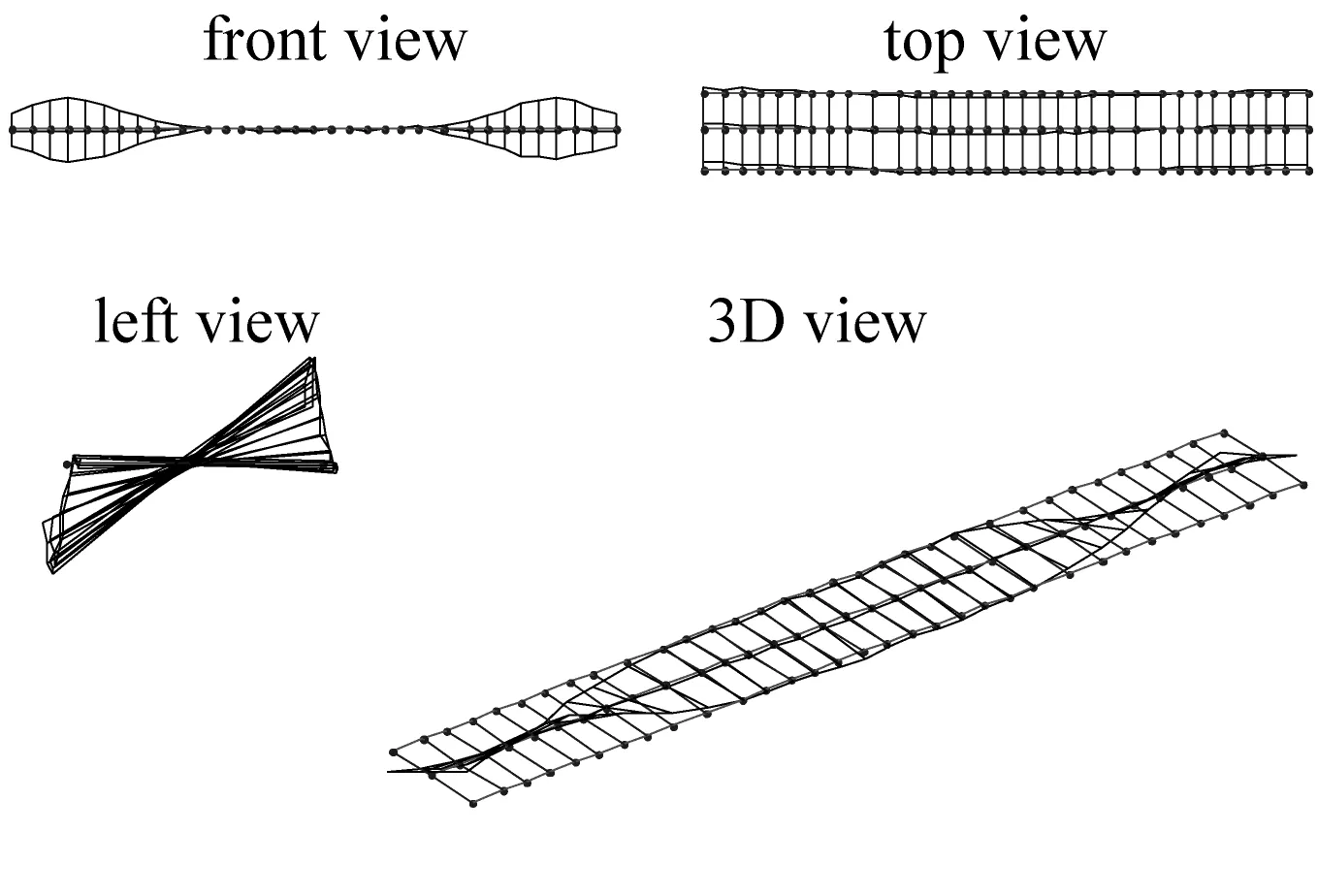
(h) 3阶扭转振型(3.787 Hz)

(i) 4阶竖向弯曲振型(4.415 Hz)
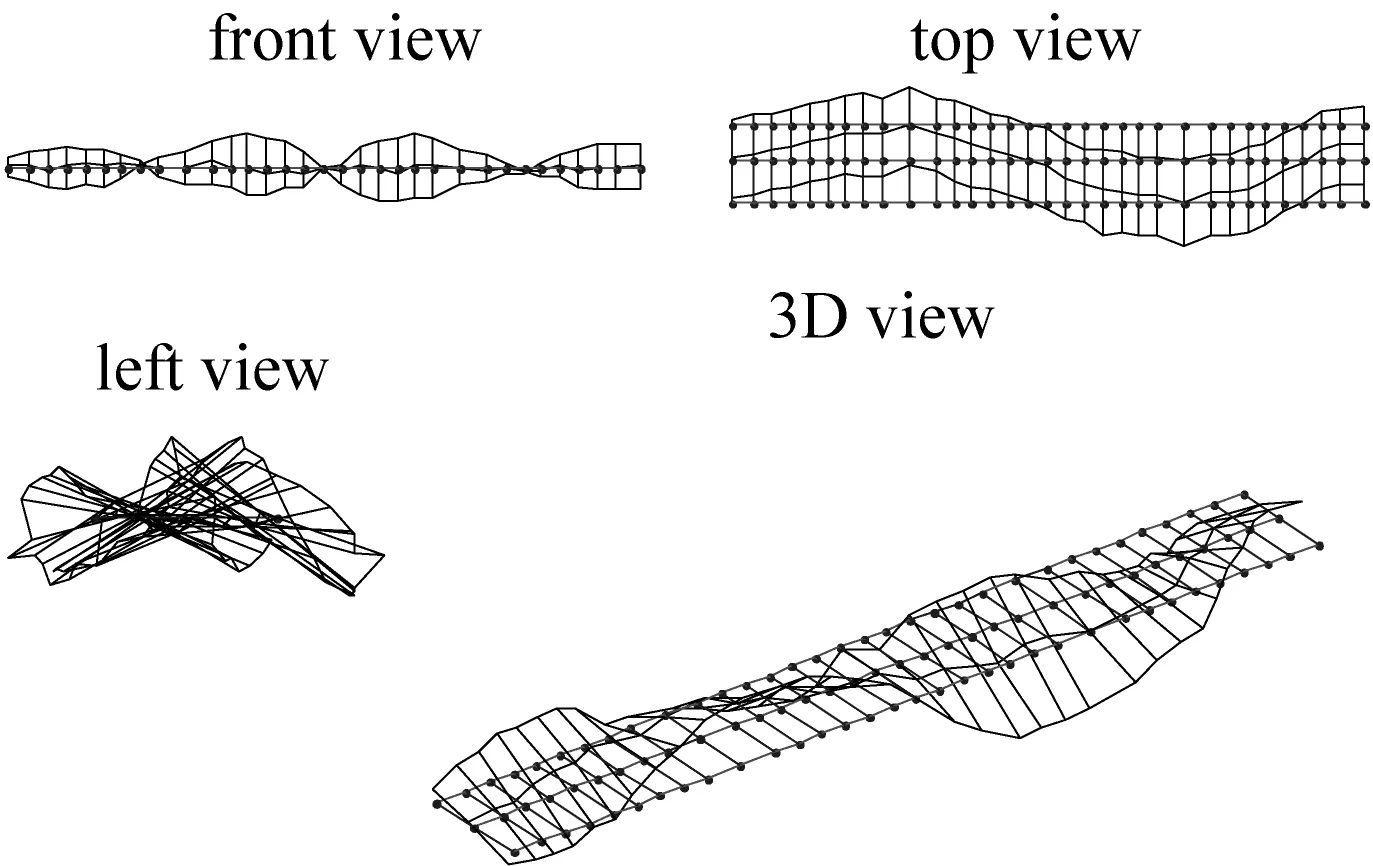
(j) 2阶横向弯曲+扭转振型(4.901 Hz)
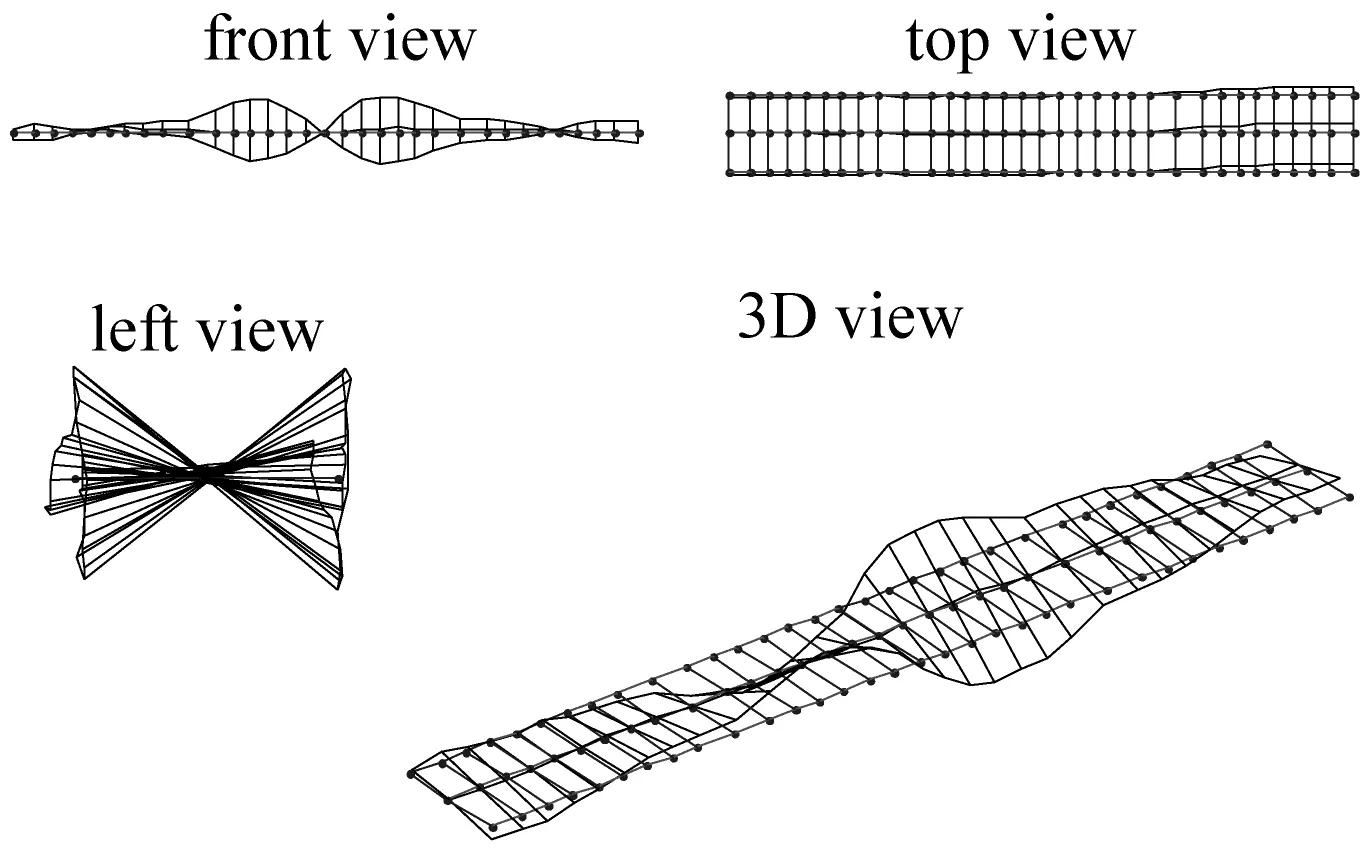
(k) 4阶扭转振型(5.706 Hz)
(8) 不同单元之间自由度不匹配时,根据相互之间的关系采用CE约束方程进行处理。全桥有限元模型如图7所示。
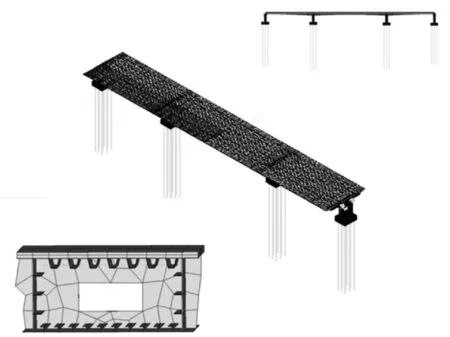
图7 桥梁有限元模型
对建立的L7联有限元模型进行模态分析,得到的模态频率与实测频率的对比数据见表2,模态振型见图8。
通过将数值模拟得到的桥梁振型并与实测振型对比,采用模态置信度值(MAC)衡量二者之间的相关度,如图9所示。
由表2与图9可知:有限元分析频率与实测频率的相对误差均在5%以内,MAC值均大于0.75,表明有限元模型分析得到的结构模态与实测桥梁模态之间具有较高的相关度,其有限元模型具有较高的精度。
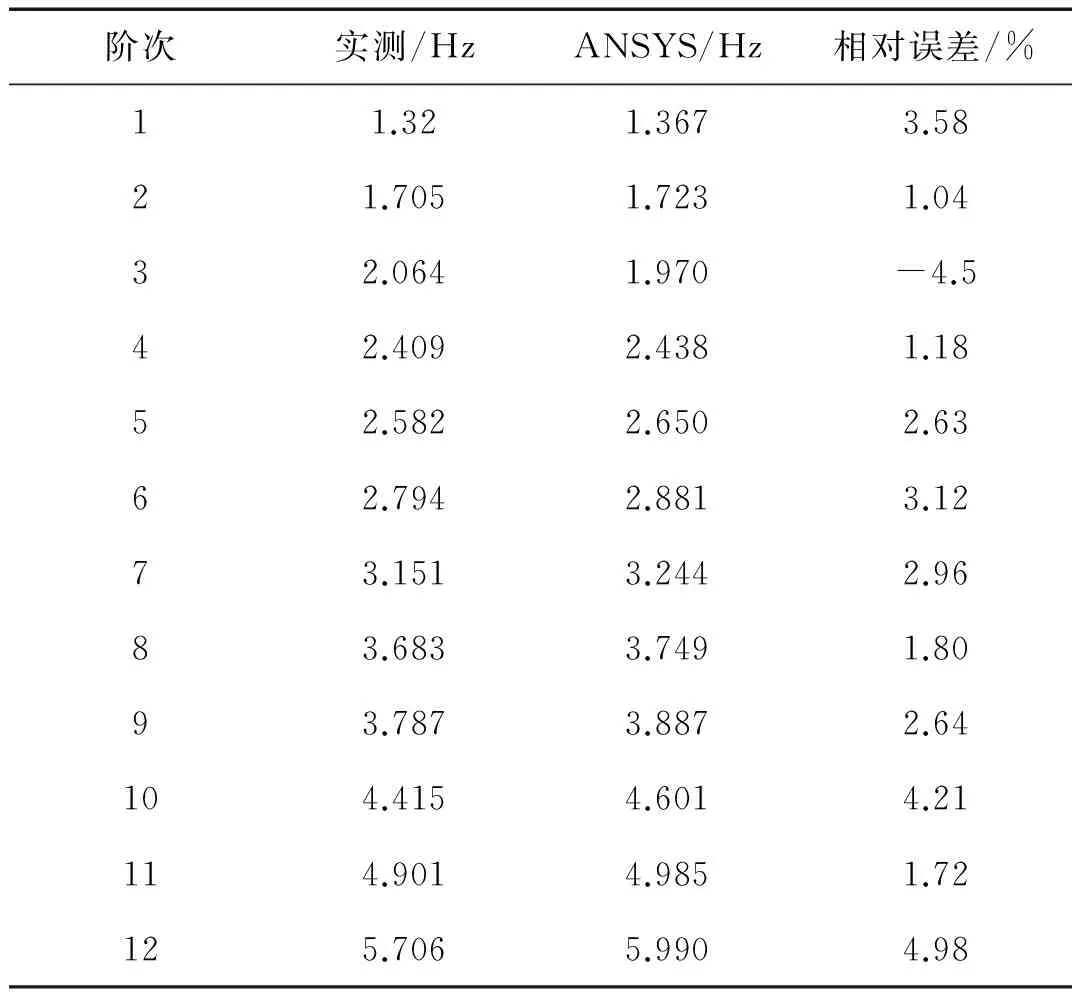
表2 实测频率与有限元频率对比表
3 基于二阶响应面法的桥梁有限元模型修正
由于在建立结构有限元模型的过程中不可避免的会产生阶次误差、参数设置误差、结构误差[20],导致有限元模型难以真实的模拟结构的实际状态,而在实际工程应用中一般总是认为实测数据更为准确和可靠,因此利用实测数据进行有限元模型修正日益受到重视[21]。文献[18]的研究结果表明:某些情况下由试验模态识别而引发的模态参数误差甚至可能已经超过了模型不精确而引起的误差,因此振型信息在模型修正中应慎重使用。结合已有的模态识别结果,本文选取前12阶固有频率的残差作为目标函数采用二阶响应面法进行桥梁有限元模型修正,具体流程如图10所示。
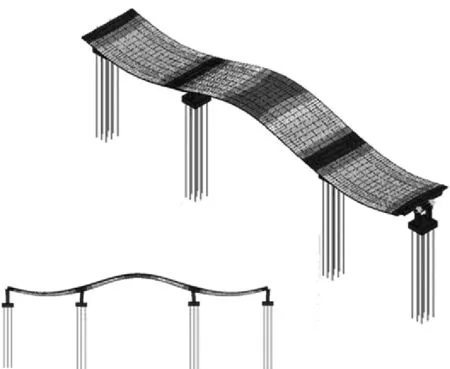
(a) 1阶竖向弯曲振型(1.367 Hz)
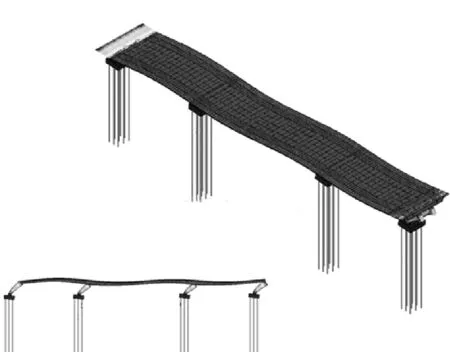
(b) 1阶纵向振型(1.723 Hz)
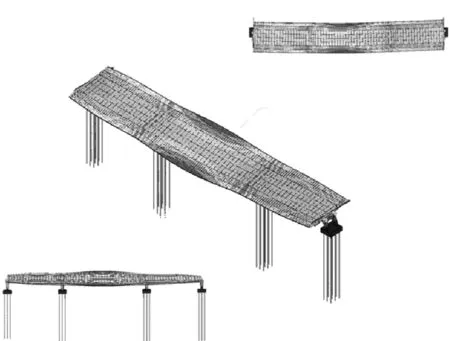
(c) 1阶横向弯曲振型(1.970 Hz)
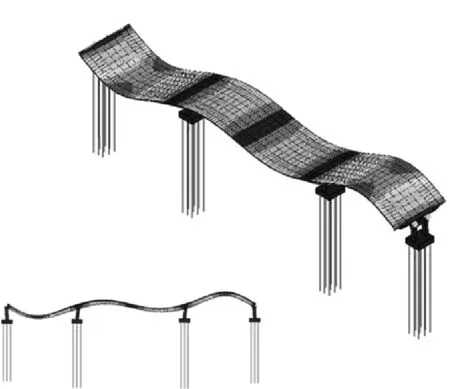
(d) 2阶竖向弯曲振型(2.438 Hz)

(e) 1阶横向弯曲+中跨扭转振型(2.650 Hz)

(f) 3阶竖向弯曲振型(2.881 Hz)

(g) 1阶扭转振型(3.244 Hz)

(h) 2阶扭转振型(3.749 Hz)
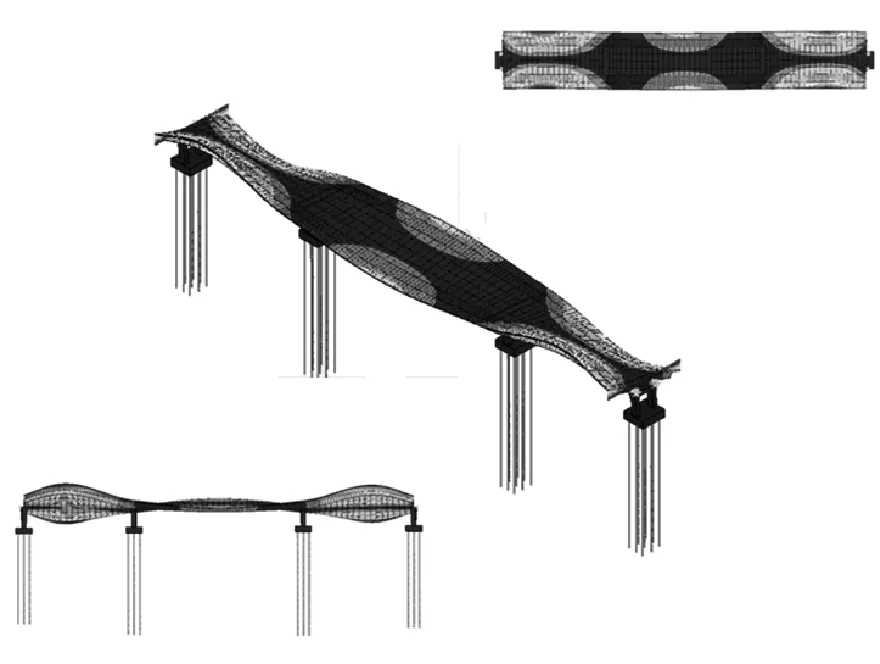
(i) 3阶扭转振型(3.887 Hz)
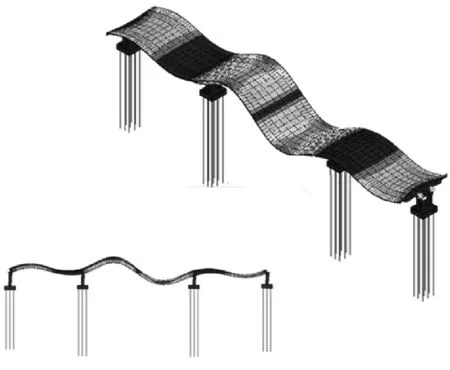
(j) 4阶竖向弯曲振型(4.601 Hz)

(k) 2阶横向弯曲+扭转振型(4.985 Hz)
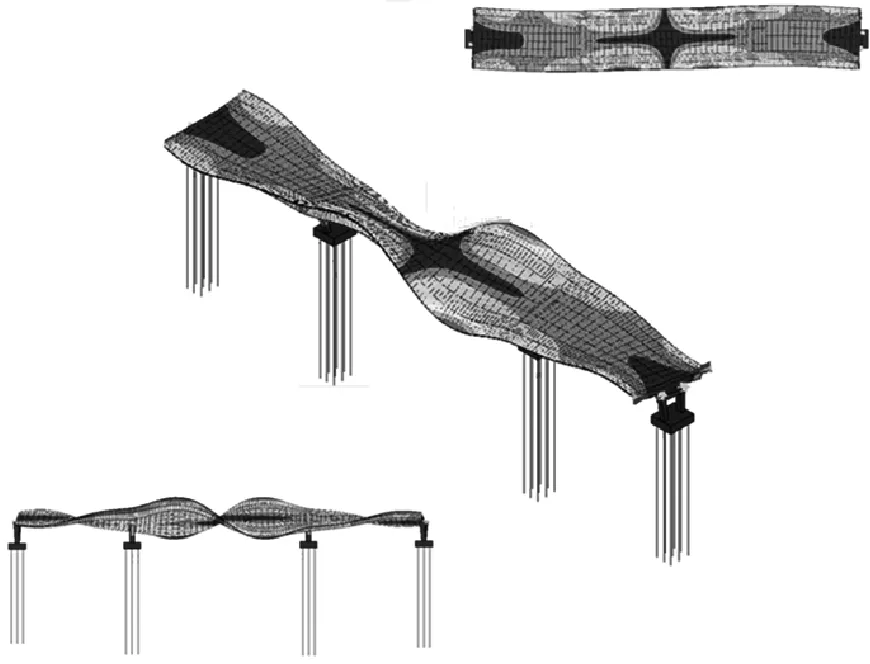
(l) 4阶扭转振型(5.990 Hz)
图8 数值模拟得到的桥梁振型
Fig.8 Mode shapes obtained from finite element analysis
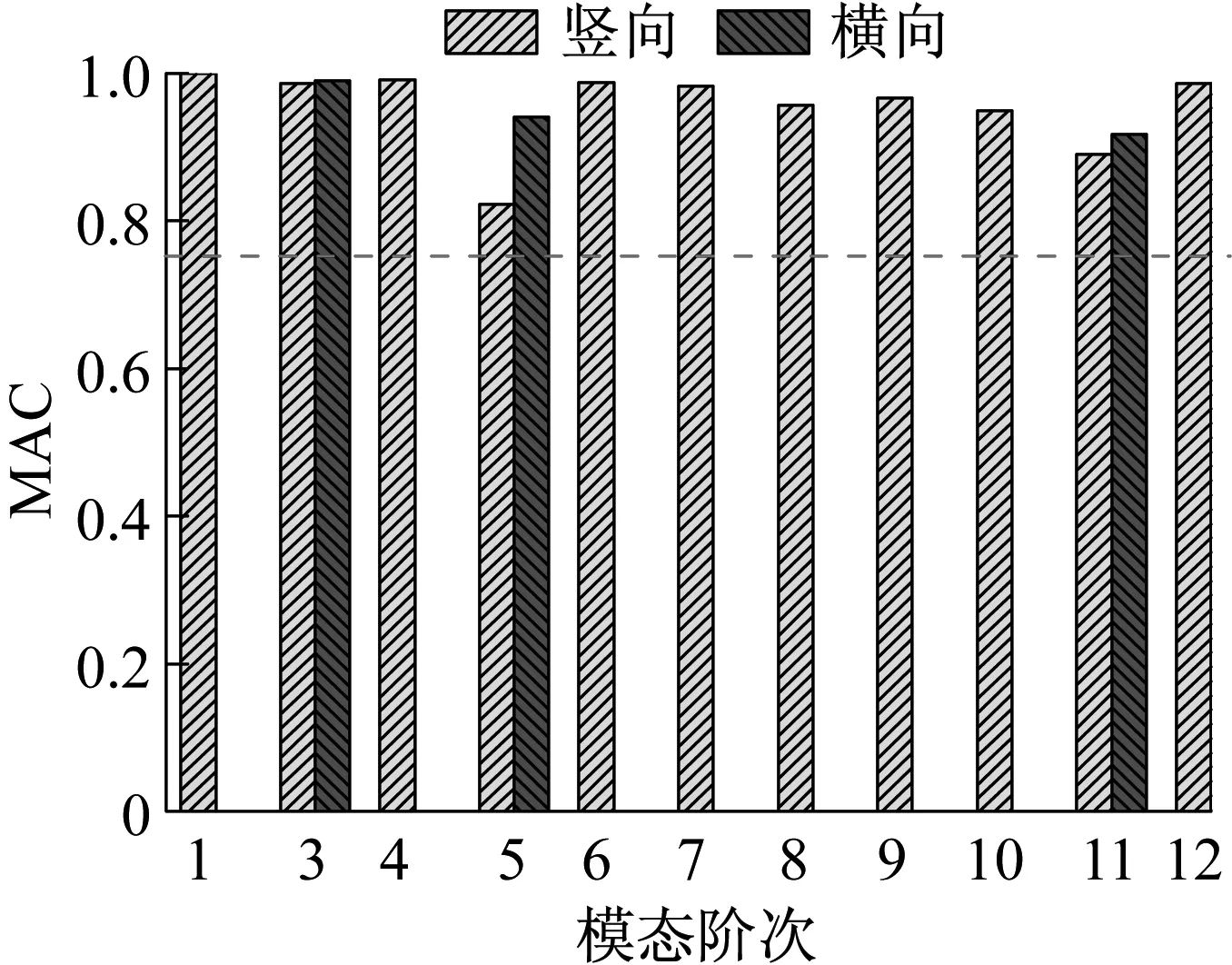
图9 模态置信度值

图10 响应面法桥梁有限元模型修正流程图
Fig.10 The procedures of finite element model updating by using response surface method
首先为避免频率残差数值过小导致出现较大的舍入误差,本文将频率残差扩大100倍作为目标函数, 然后选取若干参数采用中心差分法进行灵敏度分析,最终选取的修正参数包括:钢板质量密度、钢板弹性模量、桥墩混凝土弹性模量、沥青质量密度、伸缩缝纵向弹簧刚度,接着采用中心复合设计方法设计27次正交试验进行响应面方程拟合,拟合过程中采用F检验对各系数进行显著性检测剔除不显著的修正参数及其组合项,剔除后各个响应面方程均只有一次项系数显著,采用R2检验和相对均方根值RMSE进行精度检验,最后利用MATLAB优化工具箱中的遗传算法对目标函数进行优化求解,根据求解结果得到五个修正参数修正后的值,见表3。
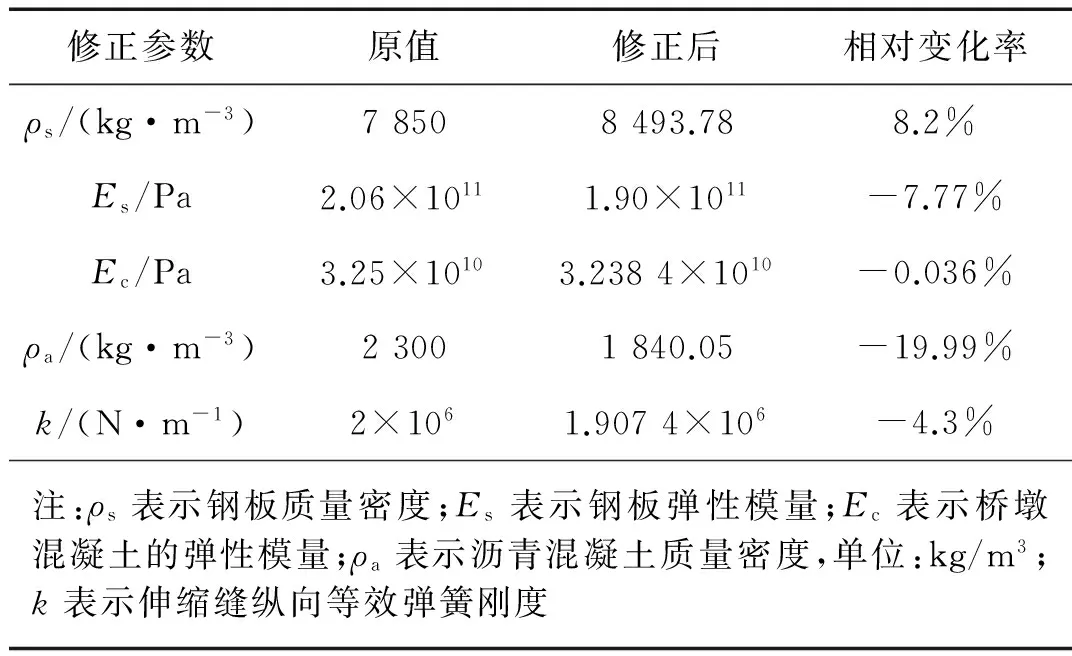
表3 修正前后各参数的值
由表3知:钢板质量密度与弹性模量有一定的变化量,这可能是由于钢箱梁焊接过程导致的,混凝土材料性质一般较稳定,其弹性模量的变化量也很微小,而沥青混凝土质量密度变化较大,这可能是由于沥青混凝土质量密度受配合比影响较大。
根据修正后的参数再次计算有限元模型的模态频率并与实测值对比,对比结果见表4。
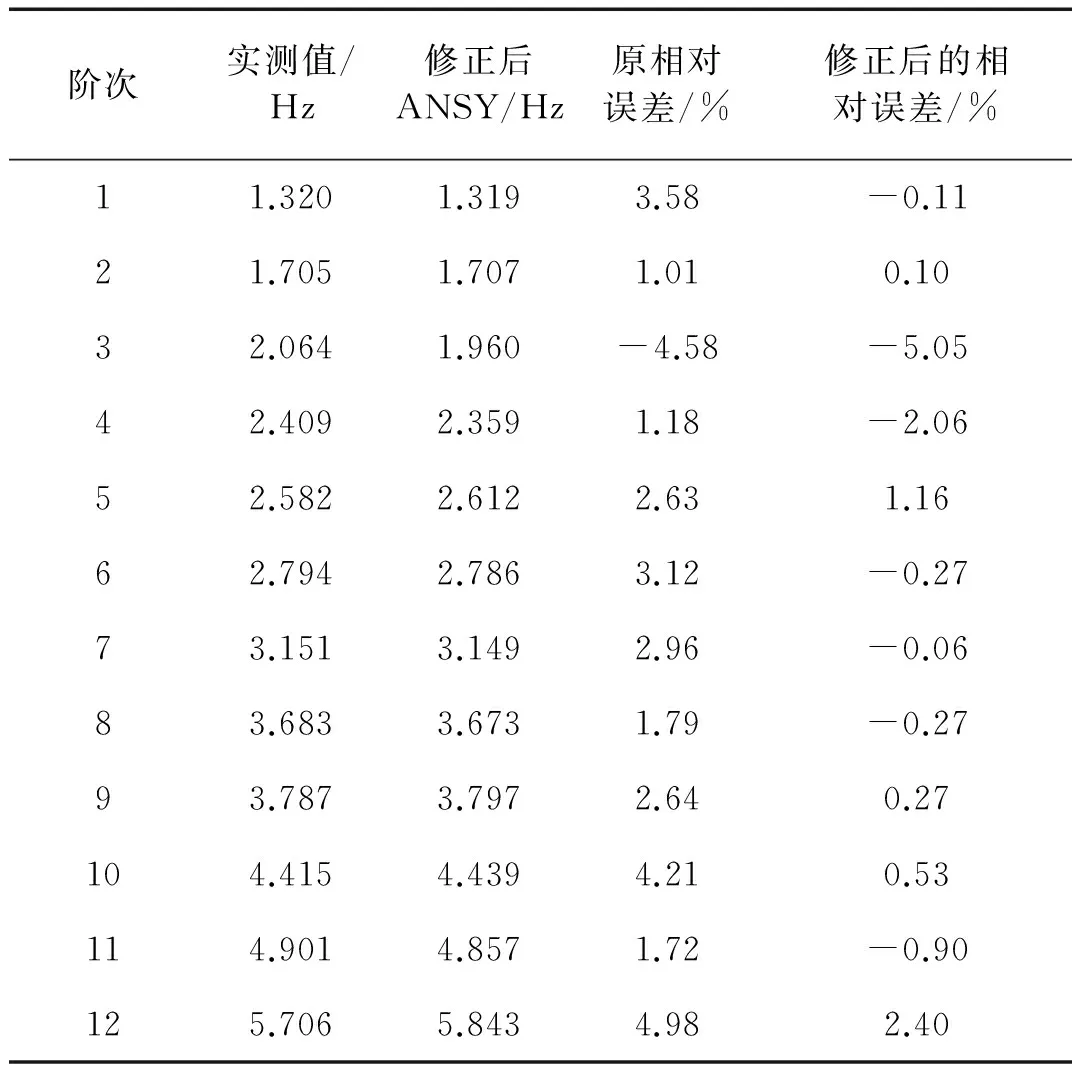
表4 修正前后频率的相对误差
由表4知:除第3、4阶频率外,经过修正后的桥梁各阶频率误差均显著减小,且均在3%之内。而第3、4阶频率误差增大的原因有以下几点:①多目标函数的优化结果是总体达到最优解(非劣解[22]),这个过程可能导致一部分目标函数达到最优,另一部分反而远离最优解;②灵敏度分析只能保证在初始值邻域范围内有效,无法对参数的全局灵敏度进行客观评价,通过灵敏度分析得到的修正参数可能并不是误差最大的参数,这可能导致部分目标函数修正效果欠佳。然而尽管第3阶频率误差略微增大,但是仅有5.05%,而其他各阶频率误差均十分微小(3阶3%以内,8阶1%以内),表明经过修正后桥梁有限元模型精度进一步显著提高。
4 桥梁各构件对动力特性的影响分析
为了给此类桥梁结构的模型建立提供指导意见,进一步研究各构件对桥梁动力特性的影响与简化方法。
4.1 邻跨等效质量的影响
由于多联布置的桥梁存在共用桥墩,邻跨桥梁将会影响共用墩的频率,已有的大量研究与实测资料[23-24]表明:当墩梁刚度比在一定范围内时,桥墩对结构的横向频率有显著的影响,结构将表现出墩梁共同作用的整体模态。
考虑邻跨质量对共用桥墩频率的影响,忽略其刚度贡献,将邻跨分配到支座的质量用质量单元模拟固结于桥墩顶部支座处,并考虑有邻跨等效质量、无邻跨等效质量两种工况进行模态分析,其分析结果见表5。
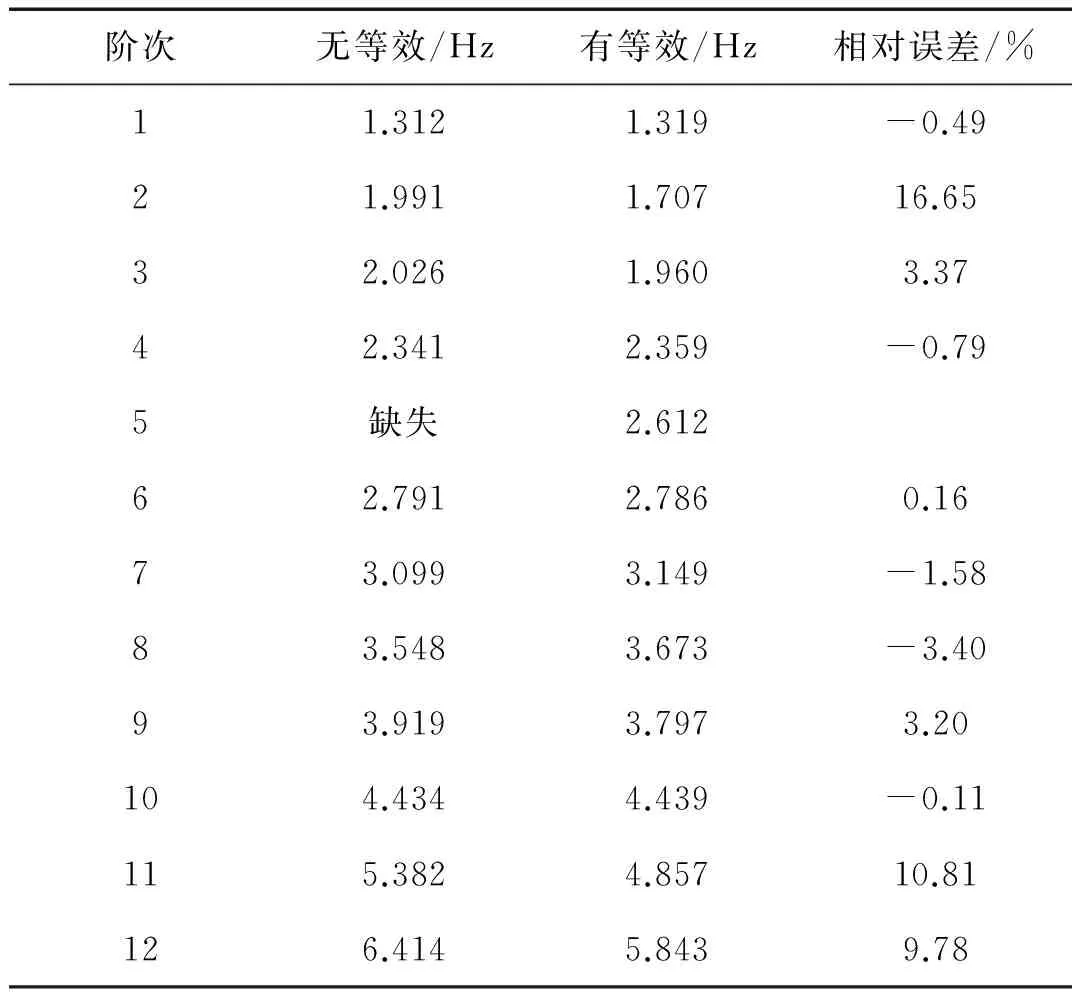
表5 邻跨等效质量对桥梁频率的影响
由表5知:邻跨等效质量对结构前四阶竖弯频率影响十分微小(1%以内),对结构的扭转模态有一定的影响(4%以内),对结构的横向模态有显著响应,使结构横向模态增大约9%~17%,甚至会导致结构的第5阶模态缺失。分析原因:邻跨等效质量作用于桥墩顶部,且等效质量为桥墩墩身自重的2倍~4倍,等效质量会显著影响桥墩横向自振频率进而影响整桥的横向模态。此外邻跨钢箱梁铺装引起的等效质量增量占总等效质量的38%,混凝土桥梁的仅占8%左右,因此等效时对于钢箱梁侧必须考虑铺装层对等效质量的影响。
4.2 铺装层的影响
桥面铺装的作用是对车轮集中荷载起到分散作用,同时保护顶板不受车辆轮胎的直接磨损,并保护桥面板免受雨水的直接冲刷。
不同类型桥梁一般采用不同类型的铺装材料,相较于混凝土材料的桥梁,钢材质桥梁会加铺一层较厚的混凝土面层,而钢箱梁质量相对较轻,此时铺装层的质量占桥梁总质量的百分比将显著增大。铺装层对结构的刚度与质量均有不同程度的贡献,如果单纯忽略其刚度贡献仅将其简化为集中质量显然不尽合理,且无相关资料表明铺装层对不同类型桥梁动力特性具有相同的影响规律,如果按照实际情况进行建模分析又会显著增大计算代价。本文第1节实测结果表明了铺装前后结构动力特性发生了显著变化,但是不能排除其他因素的干扰(邻跨等效质量的影响),为了更加明确地研究铺装层对桥梁模态的影响,本文利用shell181单元的可分层特性,对于不同层按照实际工程定义不同的厚度与材料属性,这样可以尽可能符合实际情况又不会显著增加计算量,本文桥梁铺装层如图11所示。
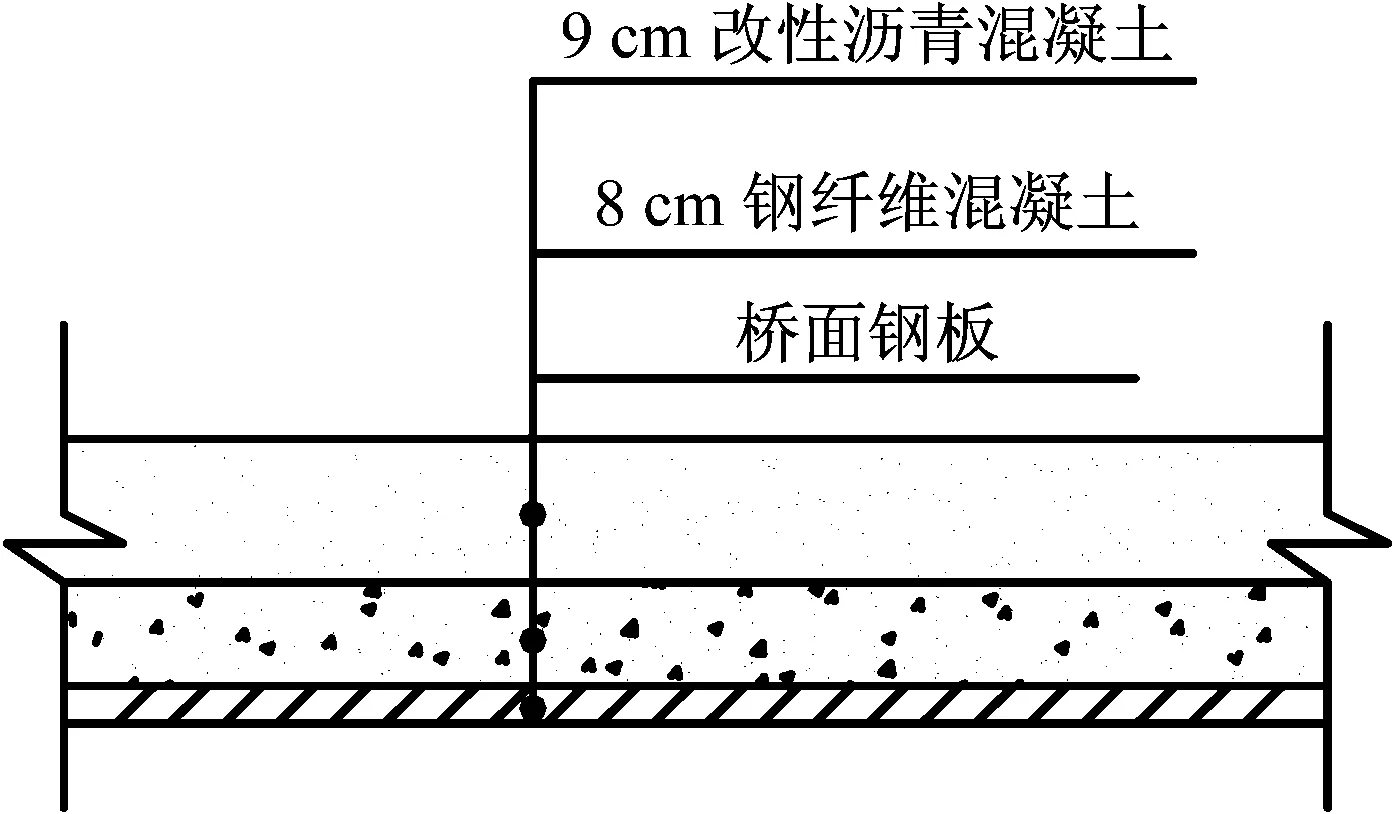
图11 钢桥面铺装层
研究如下三种工况:工况一,桥面无铺装;工况二,桥面铺装一层(8 cm钢纤维混凝土);工况三,桥面铺装两层(8 cm钢纤维混凝土+9 cm改性沥青混凝土),并进行模态分析,分析结果如表6所示。
由表6知:①相比未铺装前,铺装后桥梁结构的前十二阶频率均显著减小,减幅达12%~25%,其中一阶自振频率降低了18.56%,因此在对此类桥梁结构进行动力分析必须考虑铺装层的影响;②混凝土铺装层与改性沥青铺装层对结构频率的减幅基本相当,分析原因为钢纤维混凝土与沥青混凝土质量相差较小(前者约为后者的1.2倍),但是沥青混凝土位于上层对结构的惯性矩贡献相对较大,且结合灵敏度分析可知结构前十二阶频率对铺装层的密度较敏感,对铺装层弹性模量敏感度相对较低。本文分析得到的铺装层对桥梁模态的影响与文献[8]结果不尽相同。
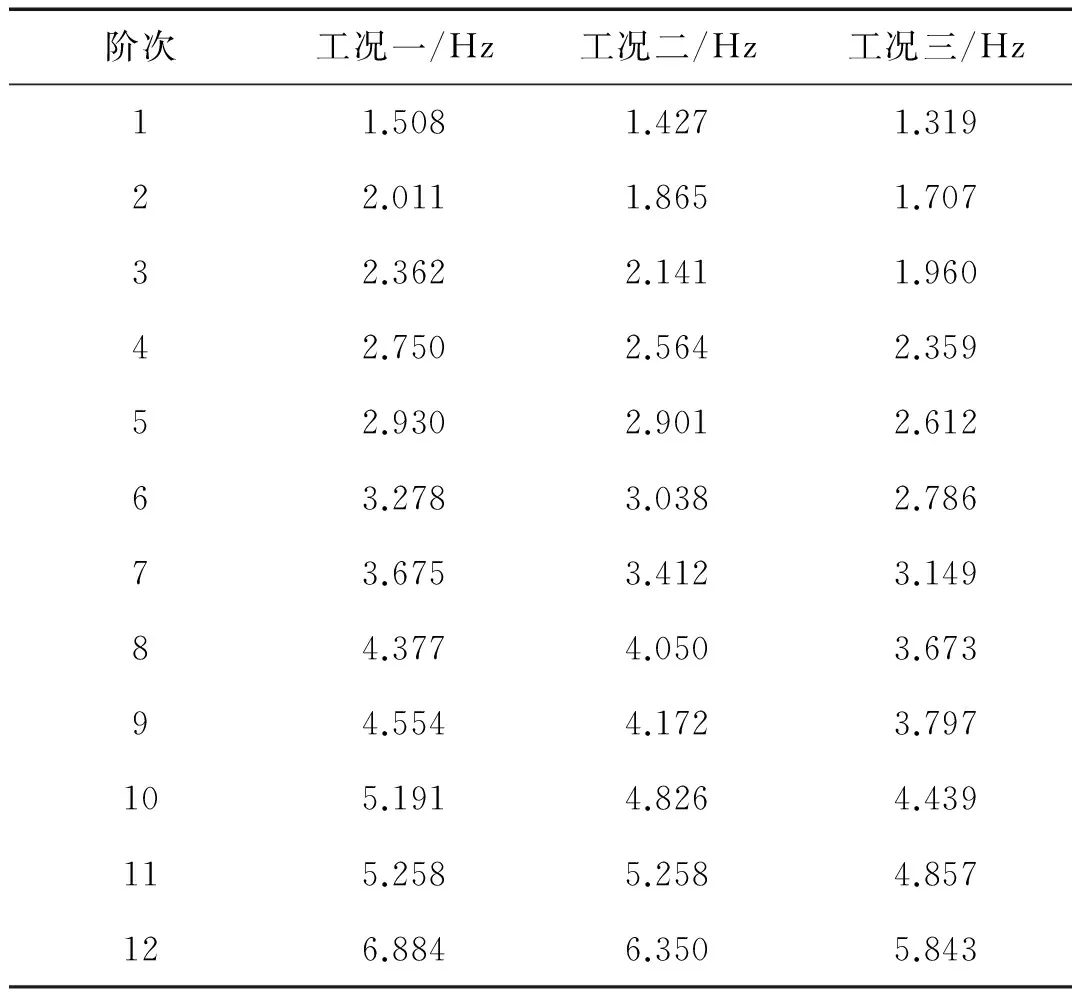
表6 不同工况下桥梁的自振频率
5 结 论
本文基于对宽幅钢箱梁桥不同施工阶段开展的模态测试工作,研究了宽幅钢箱梁桥建模方法及不同构件对此类桥梁动力特性的影响,并对桥梁有限元模型采用二阶响应面进行了修正。主要得出了以下几点结论:
(1) 宽幅钢箱梁桥模态呈现出频率低而密集、扭转模态多且靠前、横向弯曲与竖向扭转耦合、结构第一阶阻尼比较小的特征。
(2) 基于实测模态数据的二阶响应面法模型修正只采用修正参数的一次项即可以得到较高的精度,响应面法具有修正精度高、计算效率高、修正过程清晰明确的优点。
(3) 桥梁邻跨等效质量、铺装层对桥梁动力特性均有一定的影响。其中,邻跨等效质量对桥梁的横向与扭转频率有显著的影响,甚至会导致模态缺失,简化时可以考虑为集中质量放置于桥墩顶部;钢箱梁桥铺装层会显著降低桥梁各阶频率,且沥青铺装层与混凝土层影响效果基本相当,简化时可以利用板单元的分层特性来进行模拟。
通过本文的工作可以详细了解此类桥梁结构的动力特性与各构件、边界条件对桥梁模态的影响,可以为此类结构有限元模型建立、车桥耦合振动研究、结构的损伤识别、结构设计等研究提供指导意见。
[1] 张庆, 史家钧, 胡振东. 车辆-桥梁耦合作用分析[J]. 力学季刊, 2003, 24(4):577-584.
ZHANG Qing, SHI Jiajun, HU Zhendong. Coupled interaction analysis on vehicle-bridge system[J]. Chinese Quarterly of Mechanics, 2003, 24(4):577-584.
[2] 谭国辉. 桥梁与车辆相互作用的系统模拟[J].土木工程学报, 1996, 29(3):34-42.
TAN Guohui. Modeling of the bridge-vehicle interaction system[J]. China Civil Engineering Journal, 1996, 29(3):34-42.
[3] 韩万水, 王涛, 李永庆, 等. 基于模型修正梁格法的车桥耦合振动分析系统[J].中国公路学报, 2011, 24(5):47-55.
HAN Wanshui, WANG Tao, LI Yongqing, et al. Analysis system of vehicle-bridge coupling vibration with grillage method based on model updating[J]. China Journal of Highway and Transport, 2011, 24(5):47-55.
[4] LUO Q Z, TANG J, LI Q S. Finite segment method for shear lag analysis of cable-stayed bridges[J]. Journal of Structural Engineering, 2002, 128(12):1617-1623.
[5] WU Y P, LIU S Z, ZHU Y L, et al. Matrix analysis of shear lag and shear deformation in thin-walled box beam[J]. Journal of Engineering Mechanics, 2003, 129(8):944-950.
[6] 郭铁钧. 高架桥宽幅钢箱梁顶推施工技术[J].铁道标准设计, 2009,5(26):56-58.
GUO Tiejun. Wide steel box girder pushing construction technology [J]. Railway Standard Design, 2009,5(26):56-58.
[7] 陈晓龙. 钢箱梁在弯扭联合作用下的强度研究[D].长沙: 湖南大学, 2013: 41-74.
[8] REN Weixin, PENG Xuelin. Baseline finite element modeling of a large span cable-stayed bridge through field ambient vibration tests [J]. Computer and Structures, 2005, 83(8): 536-550.
[9] 何卫,谢伟平. 基于舒适度评价的大跨度车站结构精细化模型研究[J]. 土木工程学报, 2014, 47(1):13-23.
HE Wei, XIE Weiping. Study on sophisticated calculation model of large-span railway station structures based on vibration serviceability evaluation [J]. China Civil Engineering Journal, 2014, 47(1):13-23.
[10] 谭德先, 周云, 米斯特, 等. 环境激励下高层建筑结构模态测试与有限元建模分析[J].土木工程学报, 2015, 48(9):41-50.
TAN Dexian, ZHOU Yun, MI Site, et al. Ambient vibration dynamic test and finite element analysis for high-rise buildings [J]. China Civil Engineering Journal, 2015, 48(9):41-50.
[11] 宗周红, 赖苍林, 林友勤, 等. 大跨度预应力混凝土连续刚构桥的动力特性分析[J].地震工程与工程振动, 2004,24(3):98-104.
ZONG Zhouhong, LAI Canglin, LIN Youqin, et al. Analysis of dynamic characteristic of a large-span prestressed concrete continuous rigid frame bridge[J]. Earthquake Engineering and Engineering Vibration, 2004,24(3):98-104.
[12] 余印根, 宗周红, 陈宝春,等. 环境温度对连续刚构桥模态频率的影响[J]. 振动、测试与诊断, 2014, 34(1):69-76.
YU Yingen, ZONG Zhouhong, CHEN Baochun, et al. Effects of environmental temperature on modal frequency of continuous rigid frame bridge[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(1): 69-76.
[13] 夏樟华, 宗周红. 预应力对混凝土梁动力特性的影响分析[J].振动与冲击, 2007, 26(7):129-134.
XIA Zhanghua, ZONG Zhouhong. Analysis of influence of prestressing of dynamic characteristics of a concrete beam[J].Journal of Vibration and Shock, 2007, 26(7):129-134.
[14] 殷广庆. 梁式桥有限元模型建立与修正及其应用[D]. 大连: 大连理工大学, 2013: 8-17.
[15] 崔建功. 宽钢箱梁精细化模型的车桥耦合振动分析[D]. 重庆: 重庆交通大学, 2014: 61-66.
[16] 刘合旭. 宽幅连续箱梁桥车桥耦合振动分析[D]. 西安: 长安大学, 2011: 45-48.
[17] REISSNER E. Analysis of shear lag in box beams by the principle of minimum potential energy[J]. Quarterly of Applied Mathematics, 1946, 5(3):268-278.
[18] MOTTERSHEAD J E, FRISWELL M L. Model updating in structural dynamic [J]. Journal of Sound and Vibration, 1993,167(2):347-375.
[19] JONES D R. A taxonomy of global optimization methods based on response surfaces[J].Journal of Global Optimization, 2001, 21(4): 345-383.
[20] 中华人民共和国交通部. 公路桥涵地基与基础设计规范:JTG D63—2007[S].北京:人民交通出版社,2007.
[21] 战家旺, 夏禾, 李泽新, 等. 考虑土体摩擦效应的公路桥墩动力特性分析方法[J]. 土木工程学报, 2013, 46(10):74-80.
ZHAN Jiawang, XIA He, LI Zexin, et al. A method for dynamic characteristic analysis of roadway bridge piers considering soil friction effects [J]. China Civil Engineering Journal, 2013, 46(10):74-80.
[22] 苏金明, 阮沈勇, 王永利. MATLAB工程数学[M]. 北京:电子工业出版社, 2005:260-261.
[23] 张文学, 苏木标, 高军. 墩梁频率比对桥跨结构动力性能的影响研究[J]. 铁道标准设计, 2004, 36(8): 96-98.
ZHANG Wenxue, SU Mubiao, GAO Jun. A research over the impact of pier-beam frequency ratio on the dynamic performance of bridge span structure [J].Railway Standard Design, 2004, 36(8): 96-98.
[24] 岳祖润. 铁路桥梁三维耦合振动仿真与墩台状态评估[D].北京: 铁道部科学研究院, 2002: 44-60.
