移动简谐荷载作用下Kerr地基梁的稳态响应研究

黄 强， 黄宏伟， 张冬梅， 黄 栩

(1. 同济大学 土木工程学院地下建筑与工程系， 上海 200092； 2. 同济大学 岩土及地下工程教育部重点实验室， 上海 200092;3. 中铁二院华东勘察设计有限责任公司， 杭州 310006)

地表列车运行引起轨道结构响应一直是铁路工程师研究的热点[1]。随着现代铁路运行速度越来越高，列车的运行速度有可能超过下卧地层的瑞利波速而引起土层振动的剧烈增加，此时列车速度已经超过了地基-梁系统的临界速度。Krylov[2]预测当列车速度超过下卧土层的瑞利波波速时，将导致地基和轨道的急剧增加，类似于飞机突破音障而产生的音爆现象。地表轨道位移的剧烈增加势必影响到列车运行安全，因此，评估列车运行引起的轨道响应就显得十分必要。

分析地表列车移动引起的地基-梁响应最简单常见的做法是将之视为地基上无限长梁的稳态响应问题。迄今为止，对于地基梁的振动响应研究已是相当广泛。概括而言，可以归纳为三个方面：一是考虑地基模型不同，常见有单参数的Winkler地基[3]、两参数的Pasternak地基[4]、Vlasov地基[5]等，根据地基阻尼考虑与否又可相应地分为黏弹性地基和弹性地基两种情况；二是考虑梁类型不同，一般为欧拉梁(Euler-Bernoulli梁)和铁木辛柯梁(Timoshenko梁)两种；三是考虑荷载形式不同，有移动常载、简谐荷载以及分布线荷载等多种形式。例如，Kenney[6]研究了移动常载作用下Winkler弹性地基梁的稳态响应，地基梁视作Euler-Bernoulli梁。结果表明，当荷载移动速度等于无阻尼条件下的临界速度时，地基梁将发生共振，其挠度增加到无限大；Fryba[7]利用Fourier变换得到了移动常载下Winkler地基梁的挠度响应解答，详细分析了欠阻尼、临界阻尼和过阻尼三种情况下挠度解的形式；Sun[8]利用格林函数和二重Fourier变换方法得到了移动简谐均布线荷载作用下黏弹性地基梁的位移响应封闭解，分析了不同地基阻尼和荷载频率下解的形式，并对解析解进行了验证；Kargarnovin等采用Fourier变换方法和围道积分方法得到了任意分布形式移动简谐荷载作用下Pasternak地基梁的稳态响应解析解答，梁被视为Timoshenko梁，得到了梁的挠度、弯矩以及剪力响应曲线，分析了荷载速度和频率的影响；Mallik等[9]分析了Pasternak地基上欧拉梁的稳态响应，并利用Fourier变换求解方法对解析解数学表达形式进行了验证，比较了欠阻尼和过阻尼情况下位移响应的解答形式；Chen等[10]提出动力刚度矩阵求解方法，分析了移动简谐荷载作用下黏弹性地基上Timoshenko梁的动力响应，认为地基梁的临界速度和共振频率可以通过动力刚度矩阵予以确定；此外，Zhen等[11]研究了移动简谐荷载作用下弹性地基上Timoshenko梁的临界速度问题。

从已有的研究来看，目前的研究主要存在两个不足。首先，高级的地基模型较少采用。如三参数Kerr地基模型[12]；二是对于不同地基模型下的动力响应计算结果缺少对比分析，各模型的适用效果缺少进一步的验证。黄栩[13]以软土隧道上部基坑开挖引起的隧道隆起为例，比较了Kerr地基、Pasternak地基和Winkler地基模型的解析计算结果与有限元计算结果，证明Kerr地基模型与有限元分析结果为最接近，而Winkler地基梁的解析结果误差最大。但是对于动力荷载作用的情况，目前对比研究鲜见报道。

分析地基梁稳态响应，地基模型选择是最关键的因素。高级模型虽然计算过程可能更为复杂，但是其计算精度也更高，在实际应用中仍有重要的价值。目前的研究对于探讨高级地基模型响应的还较少，因此，本文利用Kerr地基模型，分析其在移动荷载作用下的稳态响应特征，最后建立地基-梁有限元模型，比较不同地基梁模型的解析结果和有限元结果差异，指出Kerr地基模型的优势。

1 Kerr地基梁稳态响应解答

Kerr地基梁模型如图1所示。假设梁为欧拉梁，Kerr地基模型由上、下两层弹簧和中间剪切层组成，模型参数为地基压缩系数k1、k2和剪切系数G，剪切层可以起到协调弹簧变形的效果。

图1 Kerr地基梁模型

Kerr地基梁的振动方程为

(1)

式中：y1，y2分别为地基梁和剪切层的挠度，m；E1I1为梁的抗弯刚度，Nm2；m1为每单位长度梁质量，kg/m；k1、k2分别上、下层地基压缩系数，N/m3；c2为地基阻尼，Ns/m3；G为剪切刚度系数，N/m；b为梁的宽度，假设为1 m；p0为荷载幅值，N；w0为荷载圆频率，rad/s；v为列车移动速度，m/s。对式(1)进行双重Fourier积分变换，将时域-空间域的振动方程转换成波数域-频域内的形式。双重Fourier变换及其逆变换形式如下

(2)

经过Fourier变换后的Kerr地基梁振动方程表达为

(3)

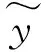
(4)

式(4)中f1(ξ,w)、f2(ξ,w)、f3(ξ,w)表达式如下

f1(ξ,w)=

(5a)

f2(ξ,w)=-(k1+k2+ic2w+Gξ2)

(5b)

f3=k1

(5c)

对式(4)进行傅里叶逆变换，并采用围道积分方法即可得到移动简谐荷载作用下Kerr地基梁挠度稳态响应解析表达式，如式(6)所示

(6)

式中:ξ1，ξ2，ξ3为ξ虚轴正半区域根和ξ实轴负半轴上的根；ξ4，ξ5，ξ6为ξ虚轴负半区域根和ξ实轴正半轴上的根。ξ1-ξ6为f1(ξ,w=w0-ξv)=0的6个复数根。在实际解答中，ξ1，ξ2,…,ξ6可能具有三种不同的根形式：只有实数部分或复数部分，或实数和复数部分都有。

2 Kerr地基梁稳态响应计算结果

各地基模型的地基参数一般可以通过简化弹性空间法换算求得[14]。Kerr地基模型的换算公式为

(7)

式中:Es、Gs分别为地基的弹性模量和剪切模量，Pa；H为土层厚度，m。本文算例中假设Es=50 MPa，泊松比v=0.3，H=15 m，可得Kerr地基参数为k1=13.33 MPa/m，k2=4.44 MPa/m，G0=128.20 MN/m。假设钢轨梁为UIC60钢轨，有E1I1=6.12×106N/m2，m1=60.34 kg/m；假设p0=80 kN。

2.1 地基梁频散曲线

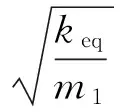
在式(6)中，必须满足w=w0-ξv，于是假设有不同w0下的w=w0-ξv直线，如图2中所示。随着列车速度v增大或w0增大，w=w0-ξv直线逐渐向频散曲线靠近，一旦w=w0-ξv直线与频散曲线相交，即有点(ξ,w)处于频散曲线上，此时f1(ξ,w)=0成立，地基梁就会发生共振，在无地基阻尼时，梁的振动挠度会趋于无穷大，有地基阻尼时，地基梁挠度则会剧增至一较大值[15]。我们把直线w=w0-ξv与频散曲线相切时的列车速度称为临界速度。可以看出，地基梁的临界速度受荷载频率的影响，荷载频率增大，Kerr地基梁临界速度会变小，如图3所示。当荷载为移动常载时，计算得到列车临界速度为537 m/s，荷载频率为20 Hz时，临界速度降为424 m/s。

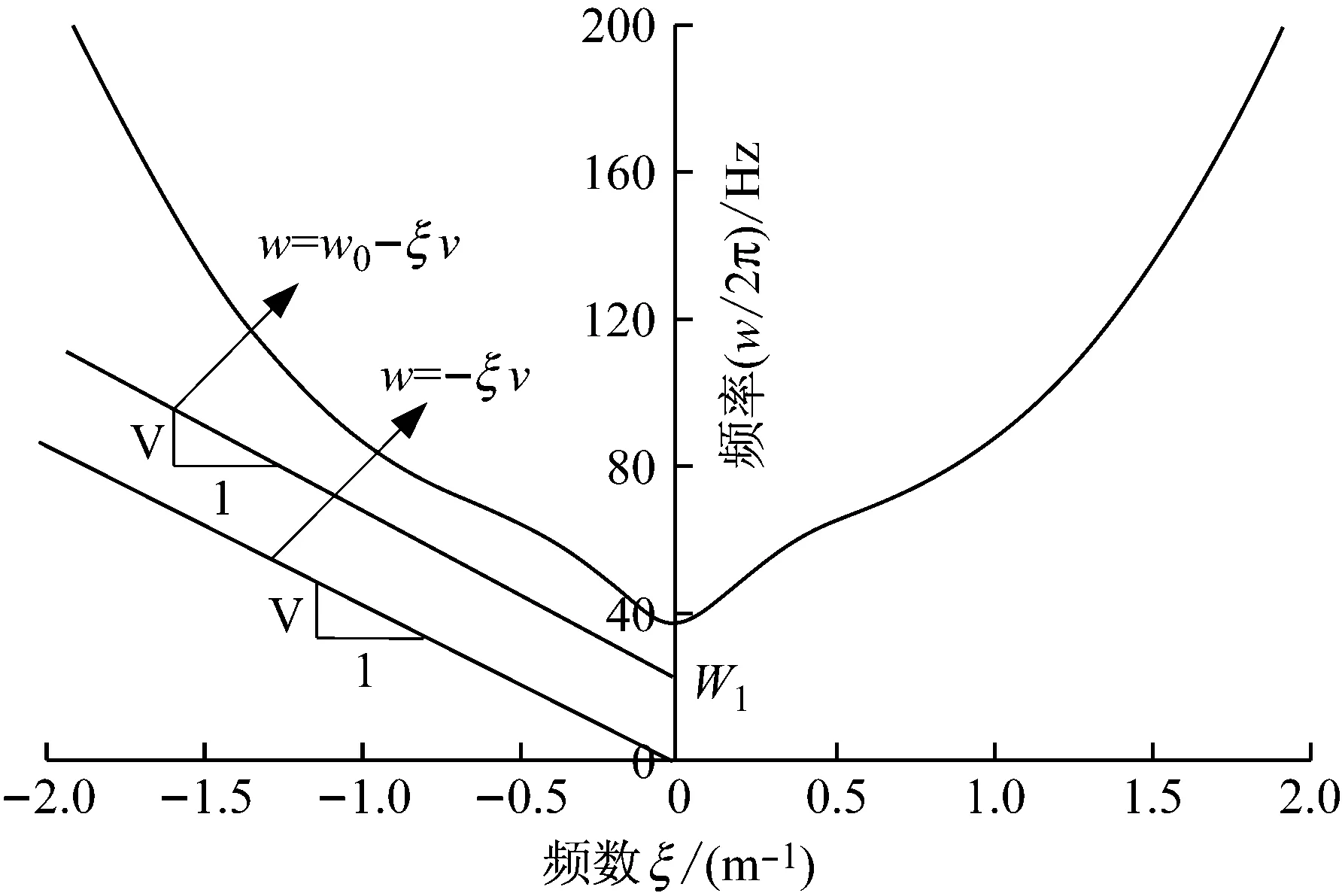
图2 Kerr地基梁频散曲线

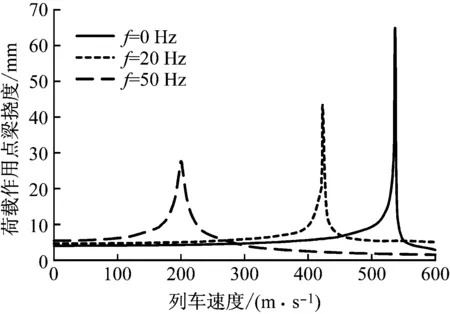
图3 不同荷载频率下Kerr地基梁临界速度

2.2 不考虑地基阻尼时Kerr地基梁响应

当不考虑地基阻尼的存在时(c2=0)，Kerr地基梁为弹性地基梁。通过计算，静载作用下梁的挠度为4.03 mm。

2.2.1 列车运行速度的影响

图3可以看出，不同的荷载频率下地基梁的挠度曲线随列车速度的变化规律相似。在列车速度未达到临界速度之前，地基梁挠度随着列车速度有轻微增加的趋势，当列车运行速度接近列车临界速度时地基梁挠度会急剧增大，而当列车速度超过临界速度后，荷载作用点的挠度急剧下降并随着速度增加逐渐减小。然而，临界速度前后地基梁的挠度响应是大为不同的。以20 Hz下的移动简谐荷载为例，不同速度下的挠度曲线如图4所示。当列车速度远小于临界速度时，地基梁挠度曲线左右对称；当列车速度接近临界速度时，最大挠度值快速增加，同时地基梁两侧会出现挠度波动现象；当列车速度超越临界速度后，地基梁挠度曲线变得左右不对称，荷载后侧方向梁的挠度出现明显起伏，存在多个峰值点，此时梁的最大挠度会在荷载移动向前方出现。

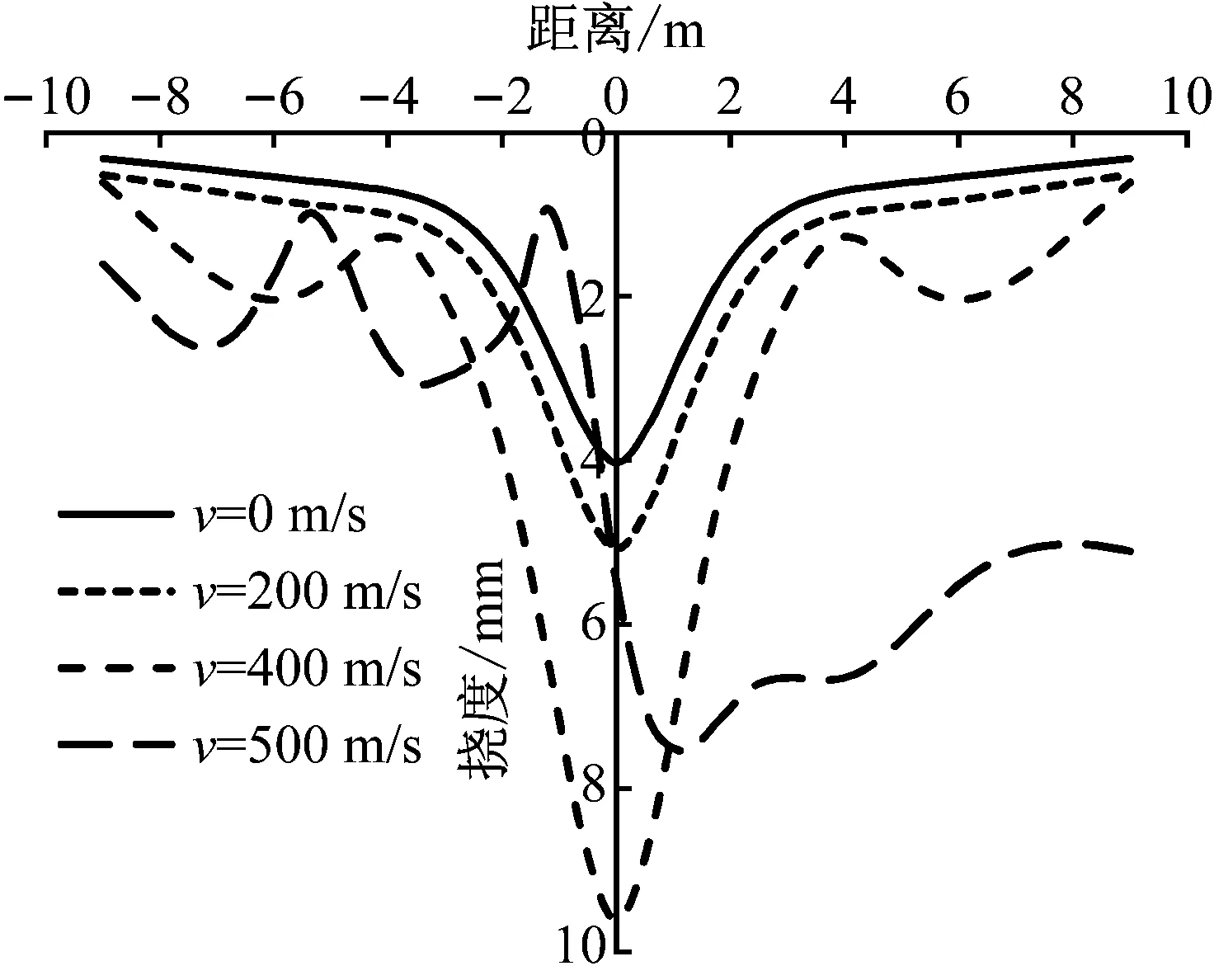
图4 列车速度对Kerr地基梁挠度的影响(f=20 Hz)

2.2.2 荷载频率的影响

荷载频率对地基梁挠度的影响如图5和图6所示。图5表明当列车速度小于临界速度时，地基梁的共振频率等于自振频率，地基梁挠度随荷载频率变化曲线几乎一致；图6表明在共振频率前后地基梁的挠度响应是不同的。未达到共振频率前，梁挠度先随着荷载频率增加逐渐增加，当荷载频率达到地基-梁自振频率时，地基梁发生共振，荷载频率继续增大时，荷载作用点处梁挠度反而减少，左右侧挠度响应不一致，与前述列车速度的影响有相似之处。造成这样的原因是，当荷载频率较小时，w=w0-ξv直线与频散曲线没有交点，故地基梁不会发生共振，当荷载频率超过了自振频率时，w=w0-ξv直线此时与频散曲线有两个交点，导致挠度曲线左右侧都会出现挠度峰值点，此时左右侧的挠度响应并不一致，出现了起伏。

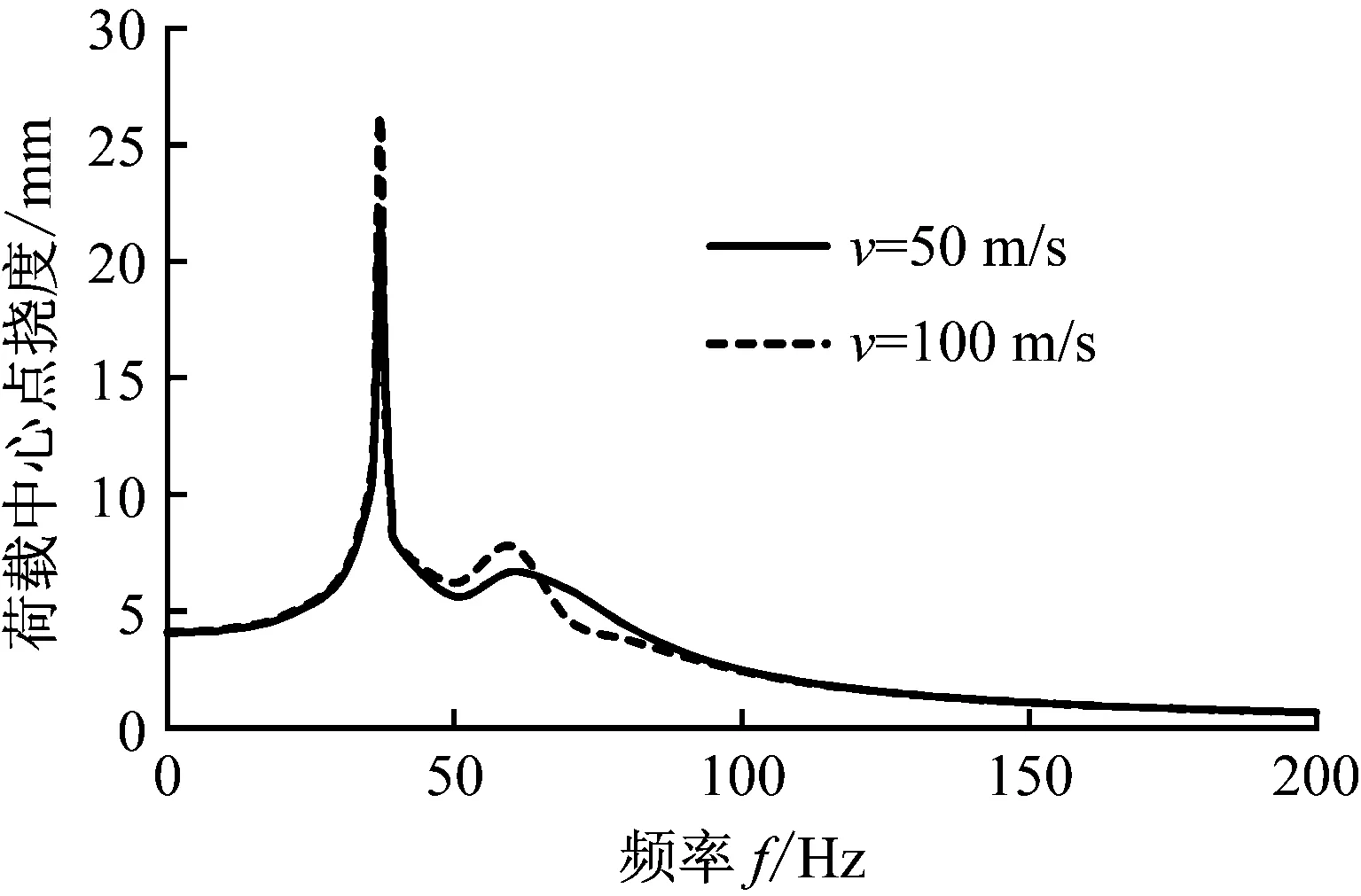
图5 荷载频率对Kerr地基梁挠度影响(低于临界速度)

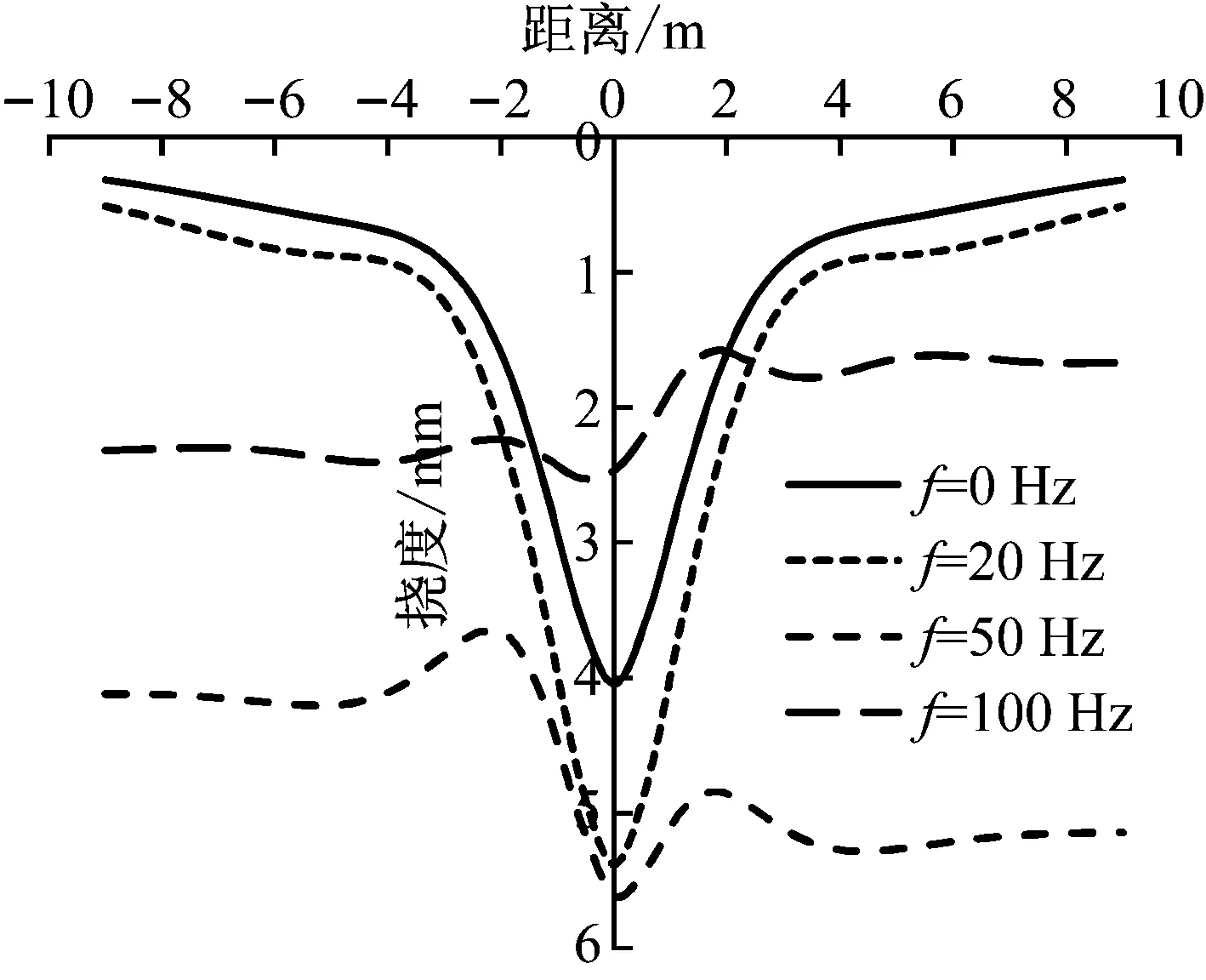
图6 不同荷载频率下Kerr地基梁挠度曲线(v=50 m/s)

2.2.3 地基压缩系数和剪切系数的影响

图7和8给出了不同地基压缩系数和剪切系数下Kerr地基梁挠度曲线。图7可以看出，地基梁挠度受Kerr地基梁上下层地基压缩系数比值影响较大。随着k1/k2比值增大(这里k2一定，k1增大)，梁的挠度会快速减少，但最终地基梁挠度会趋于稳定。这是因为随着k1/k2越大，地基弹簧的等效压缩系数越来越近k2。Avramidis等[16]认为为了获得较精确的计算结果，采用Kerr地基模型时可将上层弹簧压缩系数k1的取值调整为k1=nk2，其中n为调整系数。黄栩在其研究中认为n=7时地基梁的挠度和弯矩计算值与有限元结果最为接近。

图8为地基剪切系数对地基梁挠度的影响，可以发现随着G增大，地基梁的挠度有所减少，但改变幅度在变少，表明一味增大剪切系数G并不能有效减少地基梁的挠度，G0已满足增强地基弹簧协调变形要求。图7和8表明，Kerr地基参数中地基压缩系数比值是影响Kerr地基梁计算精度重要的因素，取k1=7k2，G=G0可满足计算精度的要求。

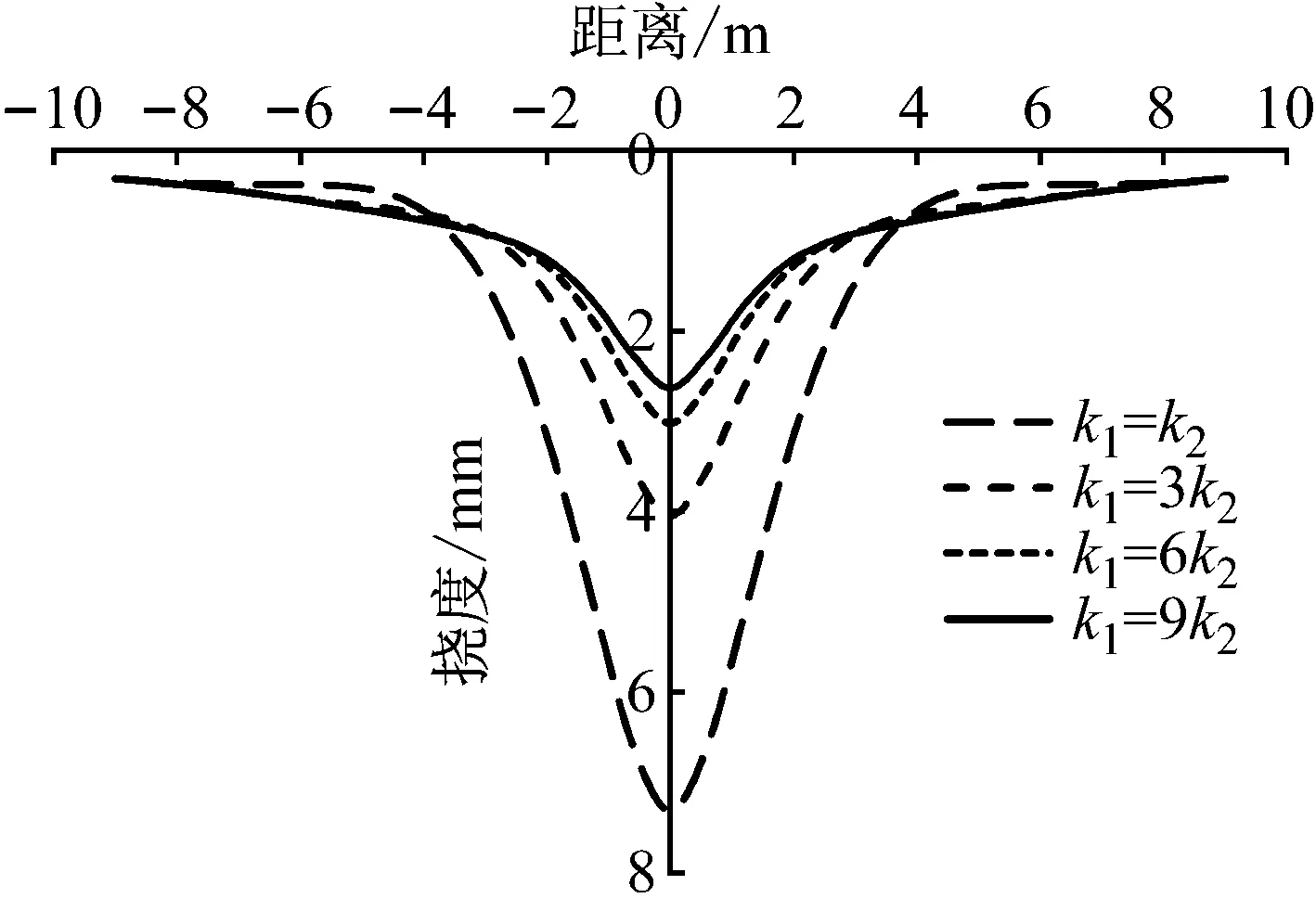
图7 k1/k2比值对Kerr地基梁挠度影响(k2=4.44×106N/m3,v=50 m/s)

Fig.7 Influence ofk1/k2on the deflection of Kerr foundation beam(k2=4.44×106N/m3,v=50 m/s)

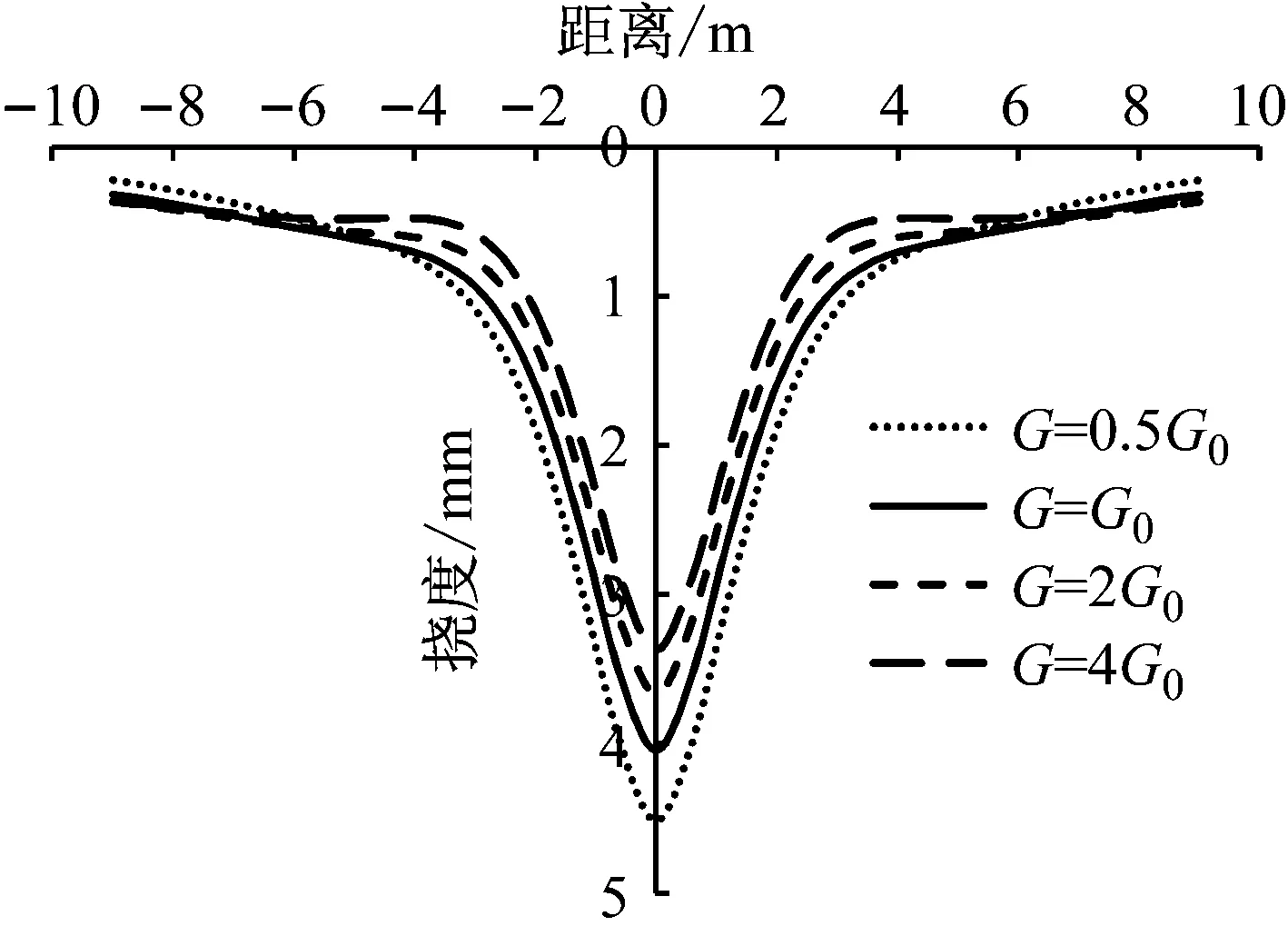
图8 剪切系数G对Kerr地基梁挠度影响(G0=

Fig.8 Influence of shear coefficientGon the deflection of Kerr foundation beam(G0=1.282×108N/m,v=50 m/s)

2.3 考虑地基阻尼下Kerr地基梁稳态响应

地基梁发生共振与列车速度和荷载频率有关，因此，可以分析地基阻尼对临界速度和共振频率的影响。地基阻尼对临界速度的影响如图9所示，地基阻尼增加会使得临界速度有轻微的增加，但阻尼继续增大，临界速度几乎不增加。其次，当荷载频率小于共振频率时，发现阻尼存在会使得地基梁挠度有所减少。在列车速度小于临界速度时，有无阻尼下的地基梁挠度响应曲线相似，而列车速度大于临界速度后，两者的挠度响应会有明显的不同，如图10所示，表明地基阻尼对超过临界速度下的地基梁挠度响应有重要影响。

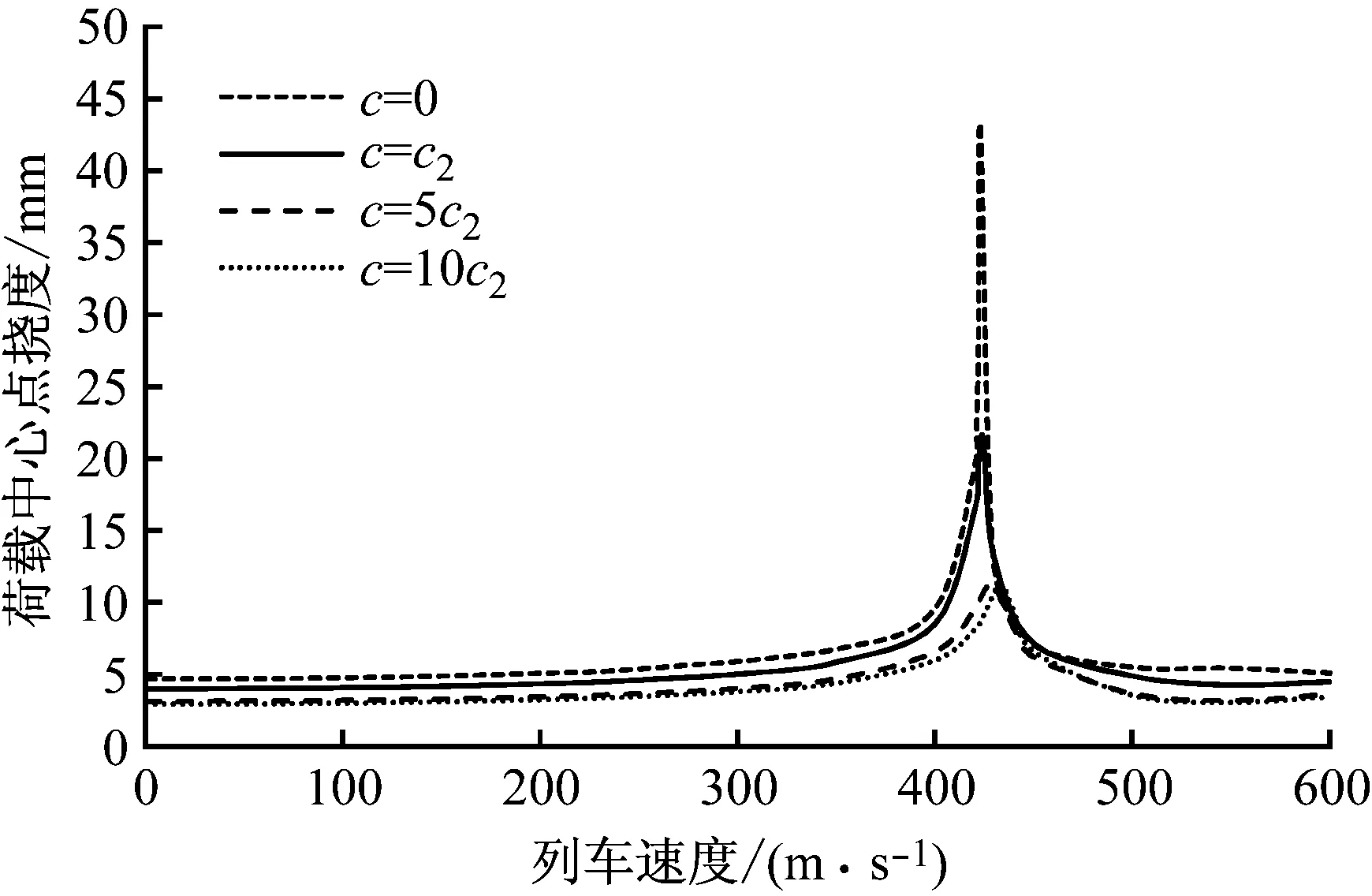
图9 地基阻尼对Kerr地基梁临界速度影响(f=20 Hz)

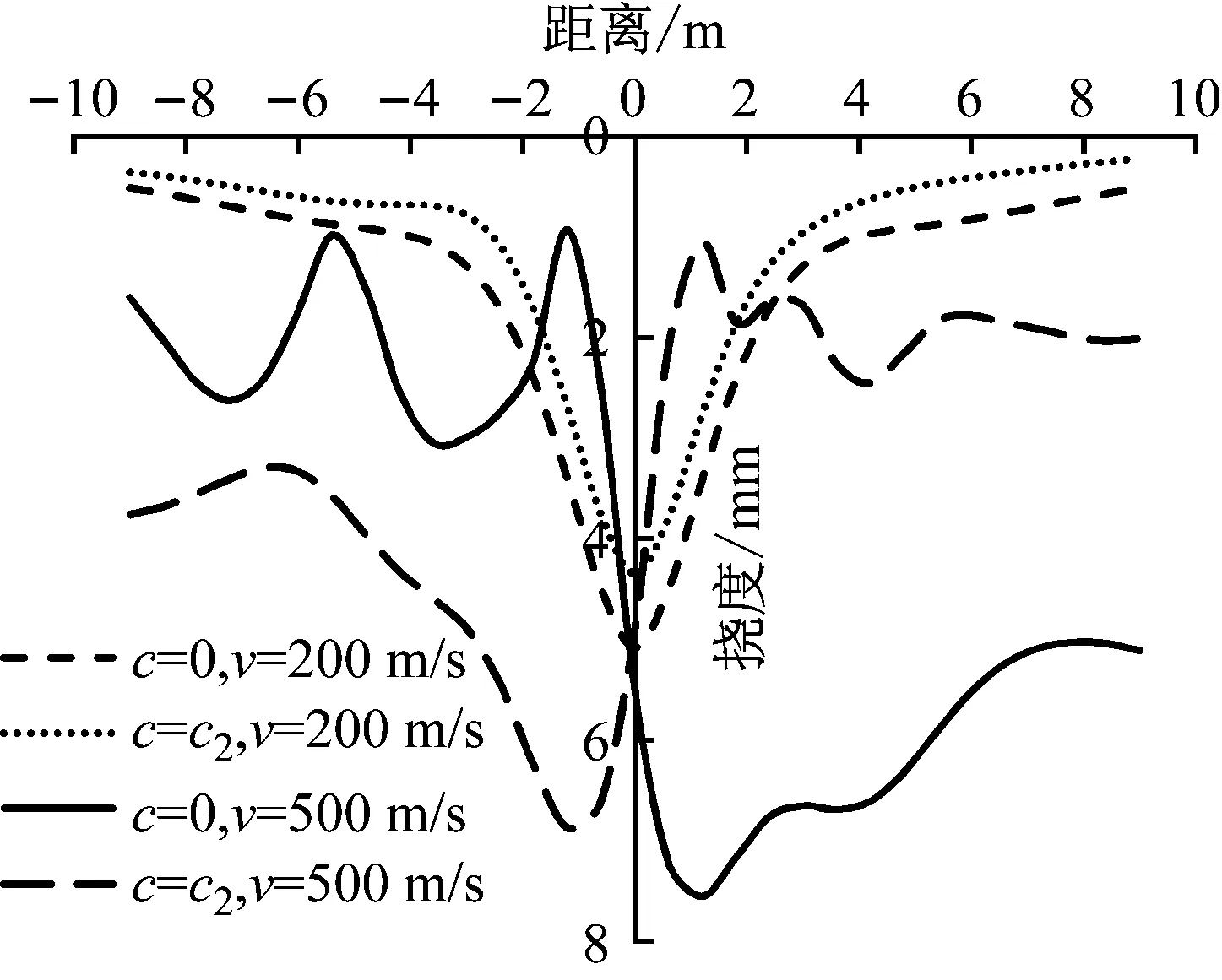
图10 有无地基阻尼下列车速度对Kerr地基梁挠度的影响(f=20 Hz)

Fig.10 Influence of train speed on the deflection of Kerr foundation beam under the existence or nonexistence of damping(f=20 Hz)

图11可以看出，当列车速度小于临界速度时，地基阻尼增加会使得地基梁的共振频率有所增加，从37 Hz增加到72 Hz，但地基阻尼继续增加时，共振频率几乎不变，但发生共振时地基梁挠度最大值会继续增大。比较有无地基阻尼时不同频率下的Kerr地基梁挠度曲线，发现两者基本一致，但是荷载频率小于共振频率时，有阻尼时的地基梁最大挠度小于无阻尼的情况，而荷载频率大于共振频率时，则是有阻尼下的地基梁挠度稍大，说明地基阻尼对超过共振频率下的地基梁挠度响应影响不大。如图12所示。

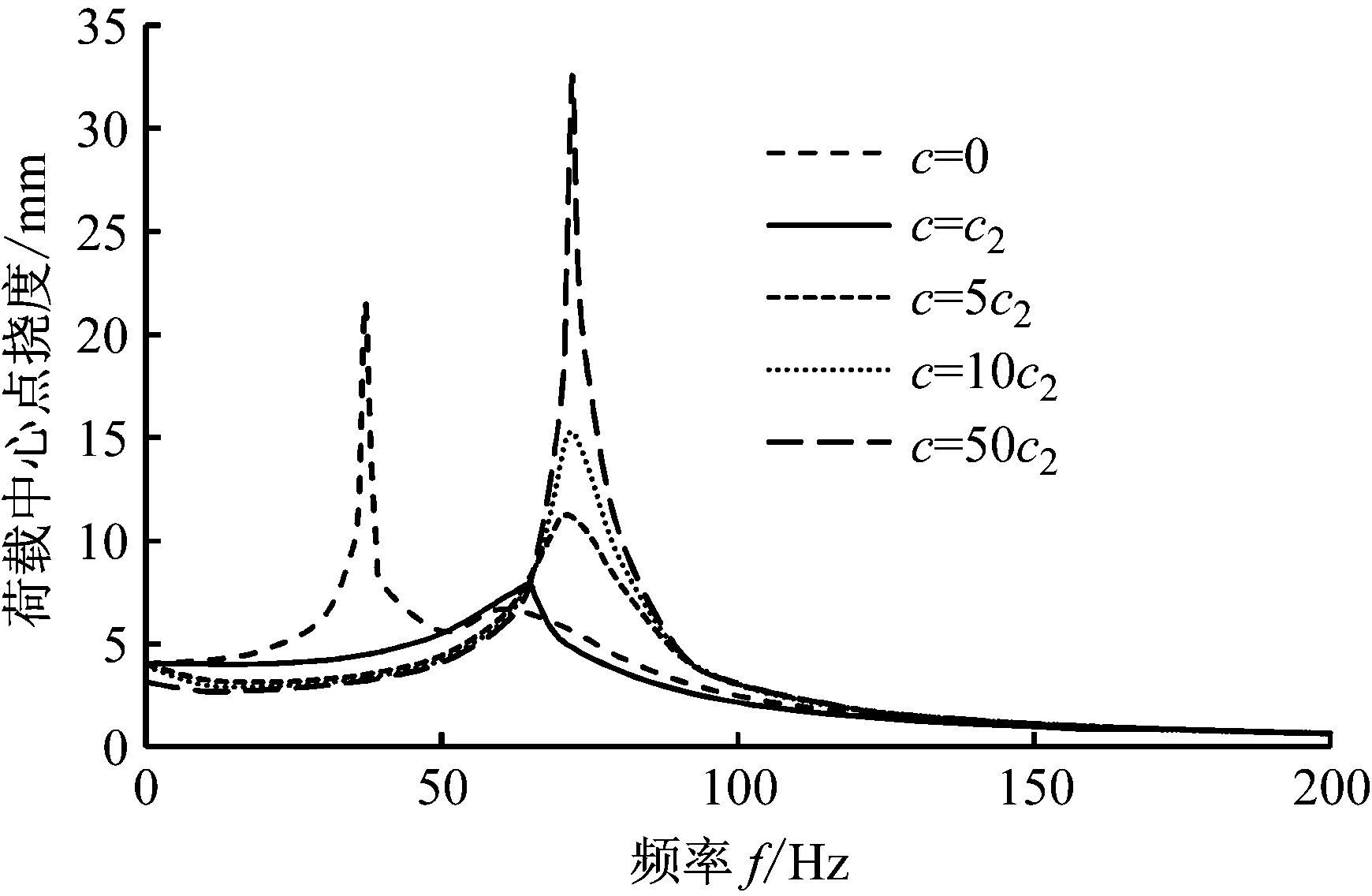
图11 地基阻尼对地基梁共振频率影响(v=50 m/s)

3 Kerr地基梁模型验证以及地基模型比较

为了验证Kerr地基梁解答的合理性，本文将Kerr地基梁的计算结果与Pasternak地基梁和Winkler地基梁进行对比。Pasternak地基梁模型如图13所示，在移动简谐荷载作用下的振动响应方程为

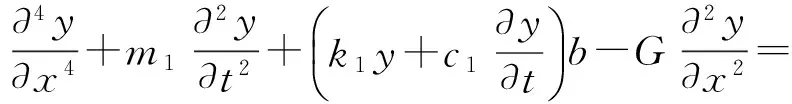
p0eiw0tδ(x-vt)

(8)

图12 有无地基阻尼下频率对地基梁挠度的影响(v=50 m/s)

Fig.12 Influence of frequency on the deflection of Kerr foundation beam in the case of the existence or nonexistence of damping(v=50 m/s)

可以看出，当Pasternak地基剪切系数G=0时，Pasternak地基就退化为Winkler地基。因而可以将Pasternak地基看作Winkler模型的改进，Kerr地基中G=0时也可退化为等效地基压缩系数下的Winkler地基，所以也是一种改进。

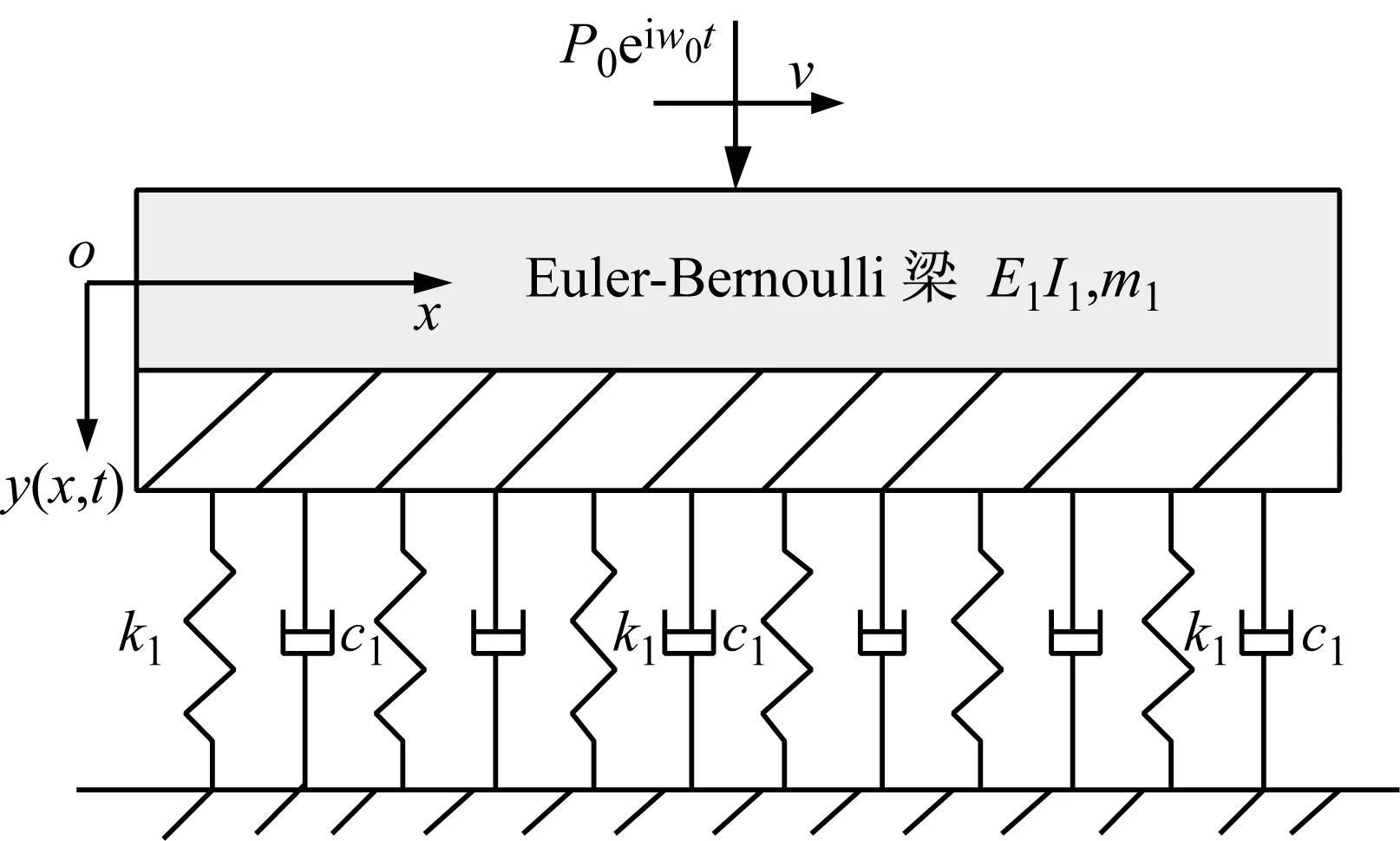
图13 Pasternak地基梁模型

为了比较不同地基梁模型的计算精度，建立二维有限元模型予以验证，如图14所示。梁为UIC60钢梁，参数如前所述，荷载频率为20 Hz，p0=80 kN。

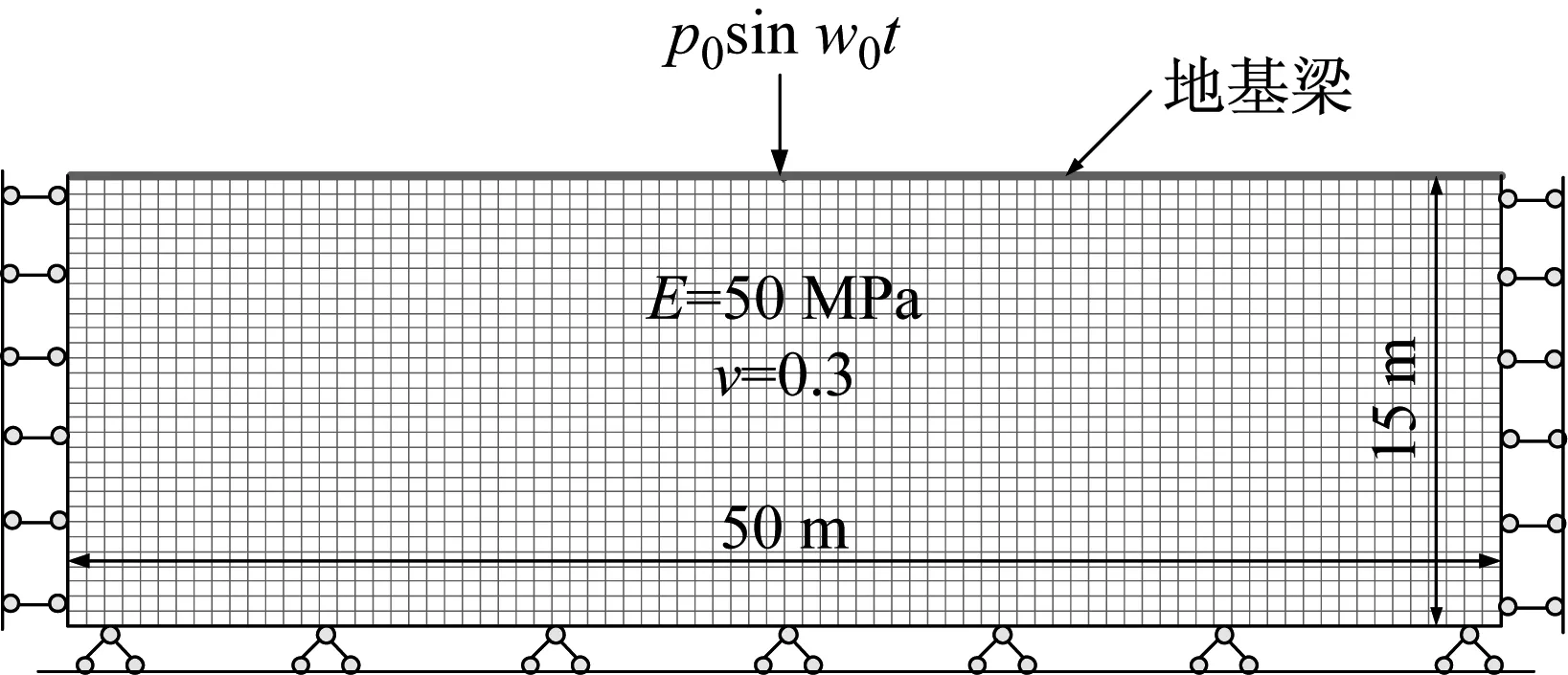
图14 二维有限元模型

根据简化弹性空间法，可以得到Pasternak地基模型和Winkler地基模型参数如下

(9)

式中:kp，Gp分别是Pasternak地基压缩系数和剪切系数；kw为Winkler 地基压缩系数。Kerr地基模型参数取k1=7k2，其他参数仍依据式(7)确定。

比较静载和简谐荷载作用下地基梁模型解析计算和有限元计算结果，如图15和16、17所示。图15可以看出，在静力荷载作用下，有限元计算结果与Kerr地基梁计算结果最为接近，且挠度曲线形态也相似，Pasternak地基梁在荷载作用点处挠度会偏小，Winkler地基梁结果与有限元结果差异最大，且挠度曲线形态与有限元结果也相差较大。由此看出，在静载作用下，Kerr地基梁的计算精度最高，Pasternak次之，Winkler地基模型误差较大。

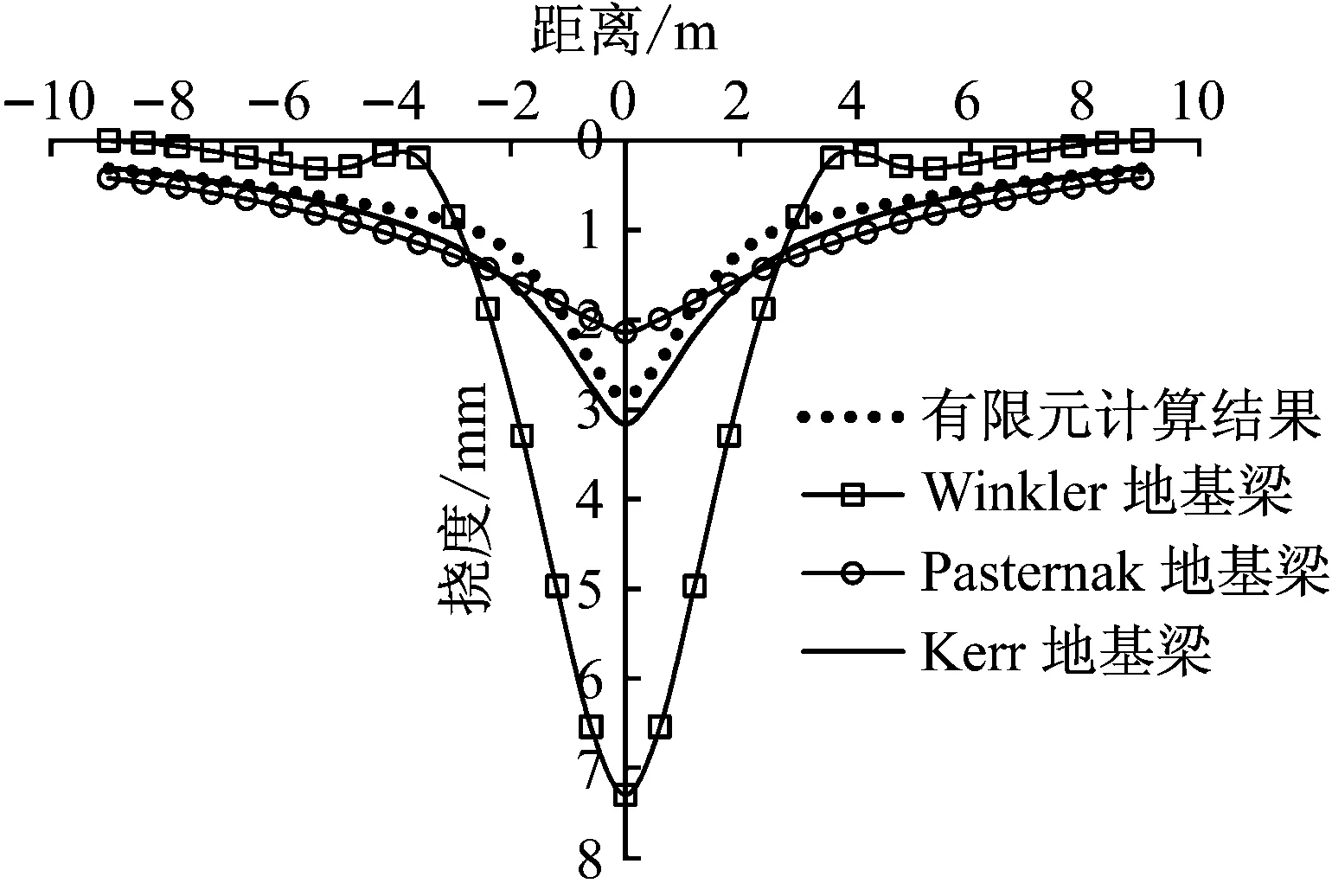
图15 静力荷载作用下各地基梁计算结果比较

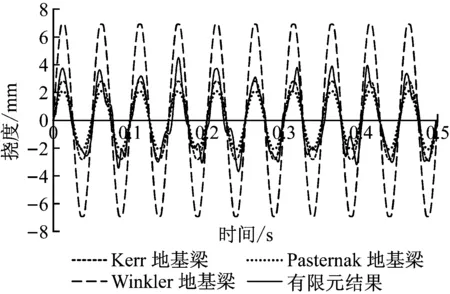
图16 挠度时程曲线对比(x=0 m)

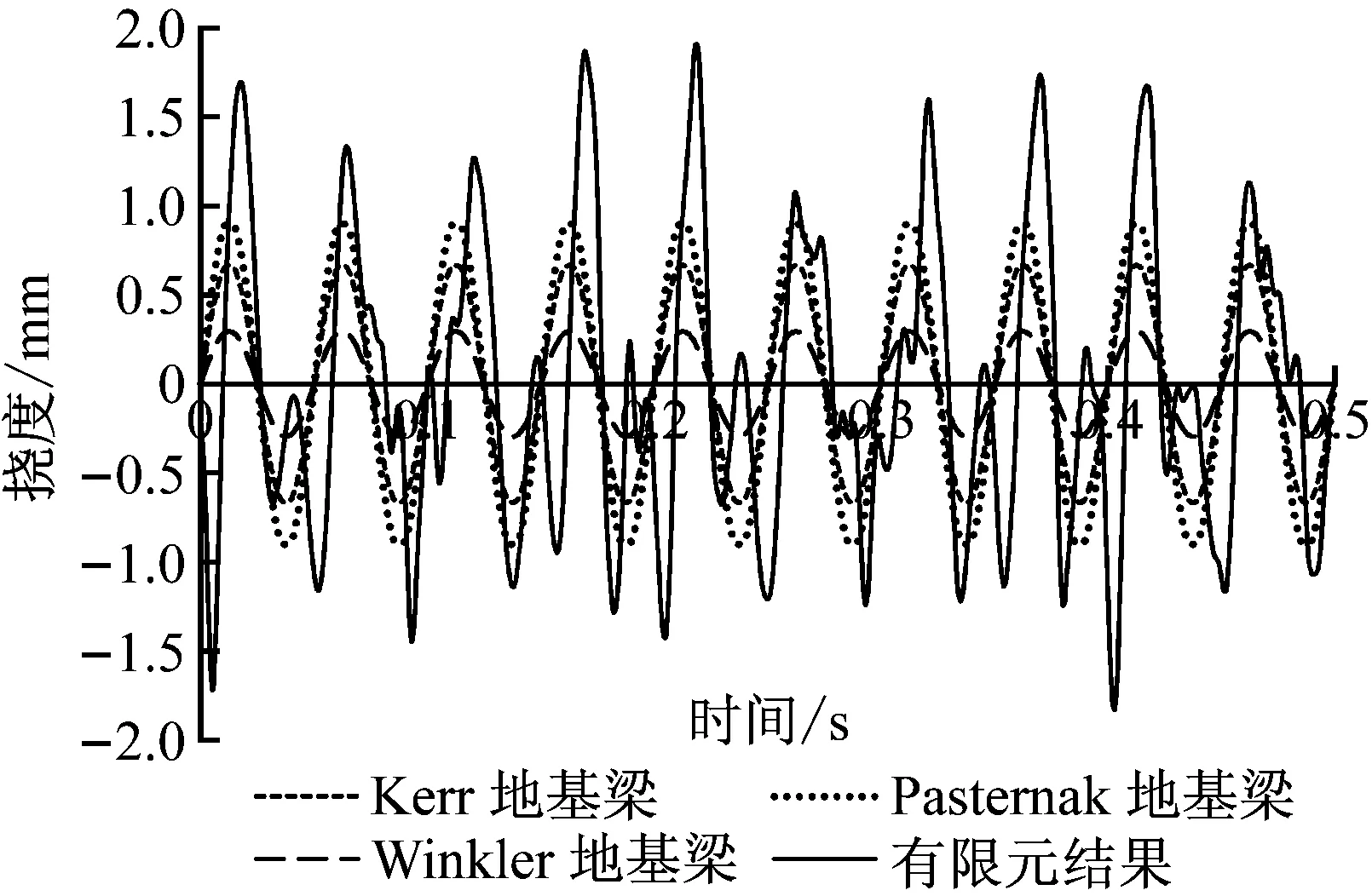
图17 挠度时程曲线对比(x=4.8 m)

图16、17比较了简谐荷载作用下有限元计算结果和解析计算结果。可以看出，动力荷载作用下，有限元结果与解析结果差异与位置有关。在荷载作用点处，有限元计算的位移时程响应与解析计算基本类似。从挠度幅值看，Kerr地基梁计算结果和有限元结果差异最小，Pasternak次之，Winkler地基梁的挠度则偏大较多。在远离荷载位置处，有限元结果和解析结果时程响应曲线相差很大，很难分辨出哪种地基梁模型更为合理。造成如此差异的原因是各地基梁模型中地基被简化为无质量的弹簧和剪切层，而有限元模型中地基是实体单元，地基模型具有质量和惯性，因而在外部动荷载作用下，有限元中梁的挠度响应不可能像各地基梁模型那样与简谐荷载时程曲线完全一致。采用地基梁模型计算结果是一种简单的近似手段。

4 结 论

本文分析移动简谐荷载作用下了Kerr地基梁的稳态响应特征，并同其他的地基梁模型比较，得到以下几个结论：

(1) 利用频散曲线可以确定地基梁的自振频率以及列车临界速度。频率-波数直线与频散曲线是否存在交点是判定地基梁响应在共振前还是共振后阶段的判定，移动荷载作用下地基梁发生共振与临界速度和荷载频率都有关，Kerr地基梁挠度曲线在临界速度或共振频率前后有明显的不同。

(2) Kerr地基梁挠度受上下层地基压缩系数比值和地基剪切系数影响，当地基系数比值和剪切系数不断增加时，地基梁挠度会趋于稳定，取k1=7k2，G=G0可满足计算精度的要求。

(3) 地基阻尼增加会使得地基梁的共振频率和临界速度有所增加，但很快达到稳定。地基阻尼的存在会一定程度上减少地基梁的挠度响应。

(4) 静载作用下，Kerr地基梁的计算精度最高，Pasternak模型次之，Winkler模型计算精度最差，在动力荷载作用下，地基梁的挠度时程响应解析计算结果与有限元计算结果差异较大，仅在荷载作用点处两者的挠度时程响应较为接近。

[1] KARGARNOVIND M H, YOUNESIAN D. Dynamics of Timoshenko beams on Pasternak foundation under moving load[J]. Mechanics Research Communications, 2004, 31: 713-723.

[2] KRYLOV V V. Generation of ground vibration by superfast trains[J]. Applied Mechanics,1995,44:149-164.

[3] WINKLER E. Die lehre von elastizität und festigkeit(The theory on elasticity and fixity)[M]. Prague: Dominicus, 1867.

[4] PASTERNAK P L. Fundamentals of a new method of analyzing structures on an elastic foundation by means of two foundation moduli[M].Moscow: Gosudarstvennoe Izdatelstro Liberaturipo Stroitelstvui Arkhitekture, 1954.

[5] VLAZOV V Z, LEOTIEV U N. Beams, plates and shells on elastic foundations[M].Jerusalem: Israel Program for Scientific Translations, 1966.

[6] KENNEY T. Steady-state vibrations of beam on elastic foundation for moving load[J]. Journal of Applied Mechanics, Transactions ASME,1954,21:359-364.

[8] SUN L. A closed-form solution of a Bernoulli-Euler beam on a viscoelastic foundation under harmonic loads[J]. Journal of Sound and Vibration,2001,242(4):619-627.

[9] MALLIK A K, CHANDRA S, SINGH A B. Steady-state response of an elastically supported infinite beam to a moving load[J]. Journal of Sound and Vibration,2006,291:1148-1169.

[10] CHEN Y H, HUANG Y H, SHIH C T. Response of an infinite Timoshenko beam on a viscoelastic foundation to a harmonic moving load[J]. Journal of Sound and Vibration,2001,241(5):809-824.

[11] ZHEN B, LUO W, XU J. Analysis of critical velocities for an infinite Timoshenko beam resting on an elastic foundation subjected to a harmonic moving load[J]. Shock and Vibration,2014(2):1-9.

[12] KERR A D. Elastic and viscoelastic foundation models[J]. Journal of Applied Mechanics, Transactions ASME,1964:31(3):491-498.

[13] 黄栩. 软土基坑开挖对下卧已建隧道的影响研究[D]. 上海：同济大学，2012.

[14] HORVATH J S. New subgrade model applied to mat foundations[J]. Journal of Geotechnical Engineering, 1983, 109(12): 1567-1587.

[15] HUSSEIN M F M, HUNT H E M. Modelling of floating-slab tracks with continuous slabs under oscillating loads[J]. Journal of Sound and Vibration,2006,297:37-54.

[16] AVRAMIDIS I E, MORFIDIS K. Bending of beams on three-parameter elastic foundation[J]. International Journal of Solids and Structures,2006,43:357-375.