含预制孔容器内爆问题的FEM-SPH耦合算法模拟

胡廷勋， 胡德安

(湖南大学 特种装备先进设计技术与仿真教育部重点实验室， 长沙 410082)

抗爆容器通常是指一定的爆炸物在其内部爆炸时，对周围环境不造成损坏和污染的一种密封抗压容器。在军事、科研、工业以及环保等领域都有应用[1]，一般用于爆轰及爆炸效应的试验研究，也可作为某种特殊要求的安全防护构件。

内爆容器实验研究成本昂贵，对实验环境和测试技术要求高，且受测试技术限制，所测实验数据极为有限。相比较于实验研究，数值计算能够更好地研究抗爆容器内部爆炸载荷的特征和分布规律。光滑粒子流体动力学(Smoothed Particle Hydrodynamics, SPH)方法作为一种具有无网格性质和拉格朗日性质的粒子法，能够很自然的捕获研究对象的运动历程，并且可以很容易地描绘出物质交界面、自由表面以及运动交界面等[2]。SPH方法的无网格特性也使得该方法可以在拉格朗日框架内处理大变形问题，克服计算中大变形相关问题，故适宜采用SPH方法对高能炸药爆炸过程进行模拟分析。但是在小变形动力学问题中，SPH方法的精度和效率总体上没有有限元(Finite Element Method, FEM)方法理想。因此，一个合理的方法就是在大变形区域应用SPH算法，在小变形区域应用传统有限元方法进行模拟分析[3]。

FEM-SPH自适应耦合算法根据等效塑性应变自动将畸变FEM单元转化为SPH粒子，既能避免单元畸变，又能减少了SPH计算区域，已成功应用到爆炸、冲击等问题的数值模拟中[4-6]。王吉等同时采用FEM算法、SPH算法和FEM-SPH自适应耦合算法模拟Taylor碰撞问题，结果显示自适应耦合算法的结果更趋近于光滑粒子法，即畸变单元转化为SPH粒子对模拟结果影响较小，无传统FEM侵蚀算法删除单元产生的误差。因此，在FEM-SPH自适应耦合算法中，可以充分发挥SPH算法模拟大变形问题无单元畸变和FEM算法模拟小变形问题效率高的特点和优势。

目前，对容器内爆问题的模拟主要采用有限差分法、有限体积法、任意拉格朗日欧拉(Arbitrary Lagrange-Euler, ALE)方法[7-9]等开展研究。基于欧拉格式的数值方法需要补充额外的算法追踪界面，并且界面追踪的精度要求越高，计算所需的时间越多。应用FEM-SPH自适应耦合算法对容器内爆问题的模拟可自然的追踪移动界面，但相关研究还比较缺乏。本文结合相关实验，采用FEM-SPH自适应耦合算法模拟含预制孔容器在内爆载荷作用下的动态响应，同时也用LS-DYNA软件中的ALE算法得到的计算结果进行比较分析，研究FEM-SPH自适应耦合算法模拟内爆问题的适用性，为内爆容器问题数值模拟研究提供有效途径。

1 FEM-SPH自适应耦合算法

1.1 基本方程

将人工黏度和人工热量考虑在内的SPH离散格式表示的Navier-Stokes方程组可写为[10]

(1)

式中：m为质量;ρ为密度;e为内能;να为速度分量;σαβ为总应力张量;xα为空间坐标;t为时间;p为各向同性压力;εαβ为黏性剪切应力;∏ij为人工黏度;Hi为人工热量;W为光滑函数。光滑函数选取三维空间的二次光滑函数，即

0 ≤R≤ 2

(2)

式中：h为光滑长度。R=r/h，r为两点间的距离。SPH方法在模拟炸药爆炸和容器内空气时总应力张量只考虑压力作用，而在模拟容器时需考虑黏性剪切应力项。

FEM相关理论已经发展的很成熟，FEM模拟爆炸冲击问题的基本方程详见文献[11]。

1.2 FEM-SPH自适应耦合算法

文中FEM-SPH自适应耦合算法采用三维四面体单元对含预制孔容器、炸药及空气进行初始离散，计算过程中，以材料的等效塑性应变为判据，当表征材料的有限单元等效塑性应变达到预设值时，单元自动转换成SPH粒子。

单元转化为粒子后，粒子的质量、速度和质心与原单元保持一致。粒子半径d的计算公式为

(3)

式中：V为有限单元转化成SPH粒子时的体积。

有限元四面体单元分三种情况转化为SPH粒子，如图1所示。单元A转化为粒子A后，在接触列表中删除三角形面a-b-c和a-c-d，增加面a-b-d和b-c-d，而光滑粒子A只能固接在一个接触面上，选择其中面积最大面进行耦合；光滑粒子B生成以后，原接触主面e-f-g、e-g-h和e-h-f被删除，新增加接触主面f-g-h，粒子B与面f-g-h耦合；单元C的四个面在转化为粒子后则全部删除，粒子C与节点k耦合。针对以上单元和粒子的耦合，本文采用Johnson提出的耦合算法进行处理，文献[12]中给出了具体的耦合算法理论和公式。耦合算法用于处理同一物体内部单元与粒子的相互作用。

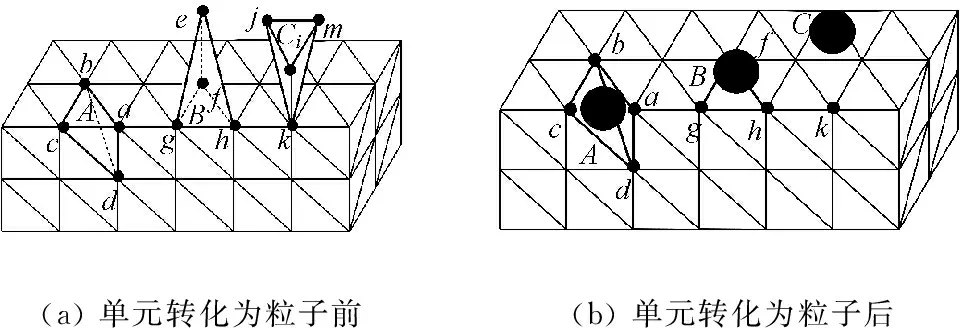
(a)单元转化为粒子前(b)单元转化为粒子后

图1 四面体单元转化为粒子示意图

Fig.1 Schematic diagram of the tetrahedral elements transformed into particles

FEM-SPH自适应耦合算法中存在三种接触，即粒子-单元、单元-单元及粒子-粒子接触，Johnson等[13-14]提出的对称接触、滑移界面算法以及粒子与单元接触算法，能较好地处理单元-单元和单元-粒子之间的接触。Campbell等[15]提出的粒子-粒子罚接触算法，可较好地处理粒子-粒子之间的相互作用。接触算法用于处理不同物体之间的相互作用。

本文所建立的模型中，炸药与空气采用共节点单元进行初始离散，炸药、空气与容器之间的相互作用采用接触算法进行计算。炸药、空气与容器的等效塑性应变判定值分别为0.05、0.01和0.5，能够保证内部炸药与空气起爆后迅速转化为SPH粒子。新产生的粒子在后续的计算中，相关物理量通过SPH方程计算，并引入单元-粒子耦合算法。随着单元不断转化成粒子，单元区域与粒子区域不断发生变化，在计算中会不断更新耦合界面。

2 材料模型

数值模拟中，TNT炸药模型采用以下本构方程[16]为

(4)

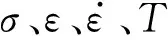
(5)

式中：Tr为室温；Tm为熔化温度。TNT炸药本构方程材料常数见表1。

空气介质在起爆后迅速转化为SPH粒子，转化时其体膨胀率比较小，计算时采用一般的黏性流体运动公式，即[17]

(6)

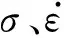
(7)

式中：E为单位体积内能；V为相对体积；C1、C2为材料常数。空气的初始内能为0，密度取1.225 kg/m3，初始相对体积取1.0，C1=C2=0.4。

对TNT炸药爆炸的压力-体积-能量特征的描述采用JWL方程，即

(8)

式中：VT为比容；E0为爆炸气体密度与初始炸药密度的比值；e为单位质量炸药的内能；A、B、R1、R2、ω为拟合系数。在计算中还会用到炸药初始密度ρ0，爆轰速度D，以及Chapman-Jouget压力PCJ。TNT炸药JWL方程相关参数见表2。

含预制孔金属容器采用Johnson-Cook本构模型和Mie-Gruneisen状态方程进行描述，即

(9)

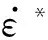
表1 TNT本构关系中的材料常数

表2 TNT炸药JWL方程参数

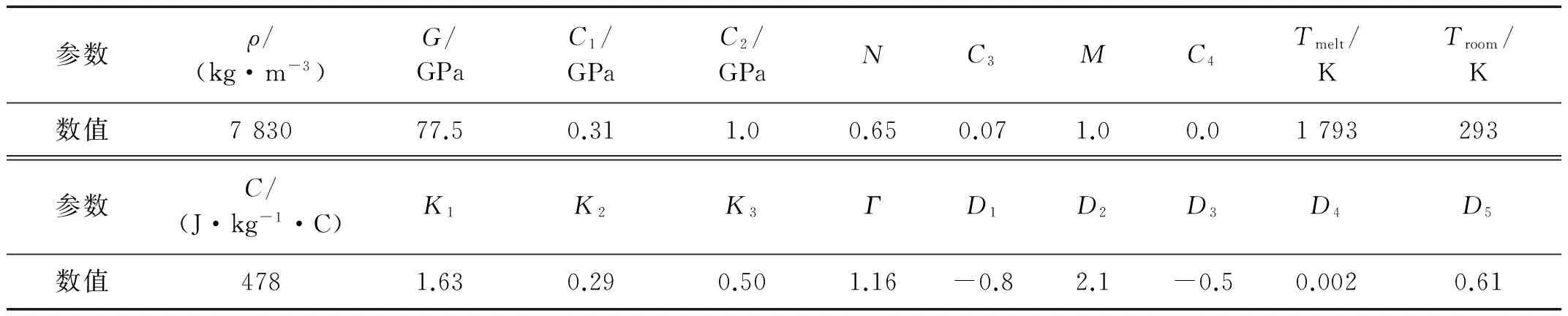
表3 金属容器材料参数

3 数值模型及结果验证

[7-9]中采用不同尺寸的含预制孔金属容器进行了内爆加载实验，实验方案如图2所示。本文建立了不同药量TNT在不同厚度含预制孔容器内的爆炸模型，数值模型与相应实验的试件尺寸、材料，预制孔形貌与位置、装药形状、装药位置保持一致。模型中TNT炸药为等长径比圆柱形。由于模型的特点，采用三维实体建模。为了减小计算规模，建立1/2对称模型。论文分别采用FEM-SPH自适应耦合算法和LS-DYNA软件中ALE算法进行模拟，如图3所示，ALE算法中采用流固耦合定义容器与内部爆炸流场的相互作用。数值模拟获取爆炸过程中筒壁的Von-Mises应力图、鼓包半径以及预制孔变化情况。通过实验结果、FEM-SPH自适应耦合算法结果及ALE算法结果的对比，研究FEM-SPH自适应耦合算法模拟内爆容器爆炸响应的有效性。

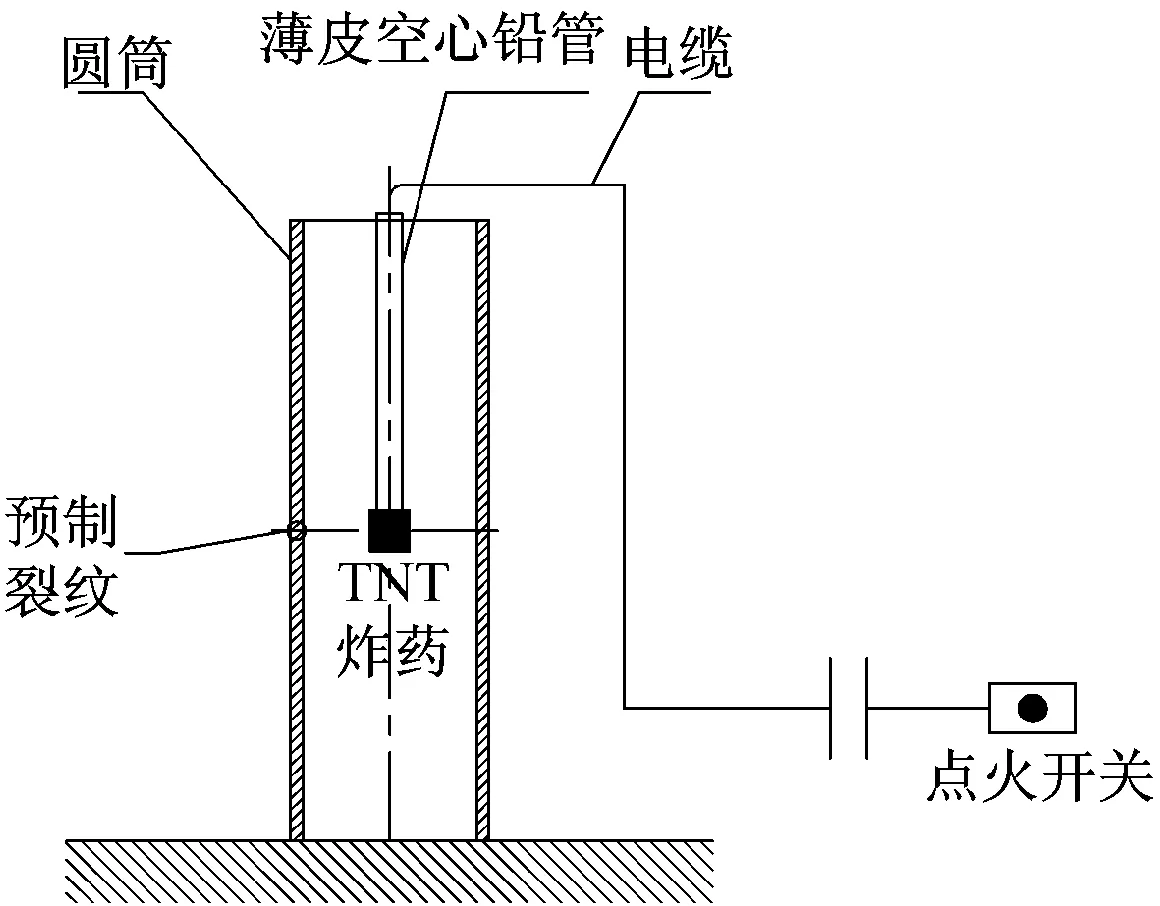
图2 实验装置示意图

为保证本文模型能够对最终破坏形貌进行准确模拟，论文参考文献[18]，将含预制孔容器可能破坏区域的计算网格尺寸设置小于1 mm。

(a)FEM-SPH模型(b)ALE模型

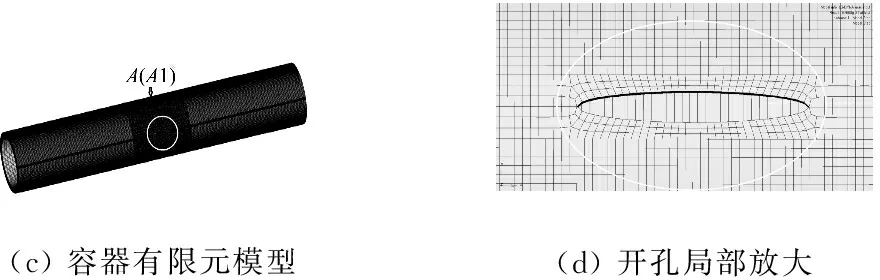
(c)容器有限元模型(d)开孔局部放大

图3 数值计算模型

Fig.3 Numerical model

3.1 15 g TNT炸药内爆加载下的薄壁容器

薄壁容器长度为250 mm，外径为76 mm，厚度为3 mm。预制孔长度为5 mm，宽度为1 mm。图4给出了实验和FEM-SPH自适应耦合算法得到的含预制孔容器在爆炸载荷作用下的最终形貌。实验以及数值模拟得到最终的鼓包半径、收缩长度、预制孔宽度及长度如表4所示。另外，由于参考文献中实验没有给出内爆加载下薄壁容器的动态响应过程量，论文进一步选取即有大变形又远离预制孔应力集中区域的A点(示意图如图3(c)所示)的Von-Mises应力值随时间变化曲线对比分析ALE算法与FEM-SPH自适应耦合算法。由数值模拟结果可以知道，A点应力值在50 μs左右达到最大值，故选取0～70 μs时间段进行比较研究，如图5所示。从图表中可以看出，采用FEM-SPH自适应耦合算法得到的结果与LS-DYNA软件中ALE算法模拟得到的结果及实验结果都比较吻合，定性的验证了FEM-SPH自适应耦合算法模拟薄壁容器内爆问题的有效性。

(a)实验结果(b)FEM-SPH模型计算结果

图4 薄壁容器实验和数值模拟获得的最终形貌

Fig.4 The final morphology obtained by the experiment and numerical simulation for the thin-walled vessel

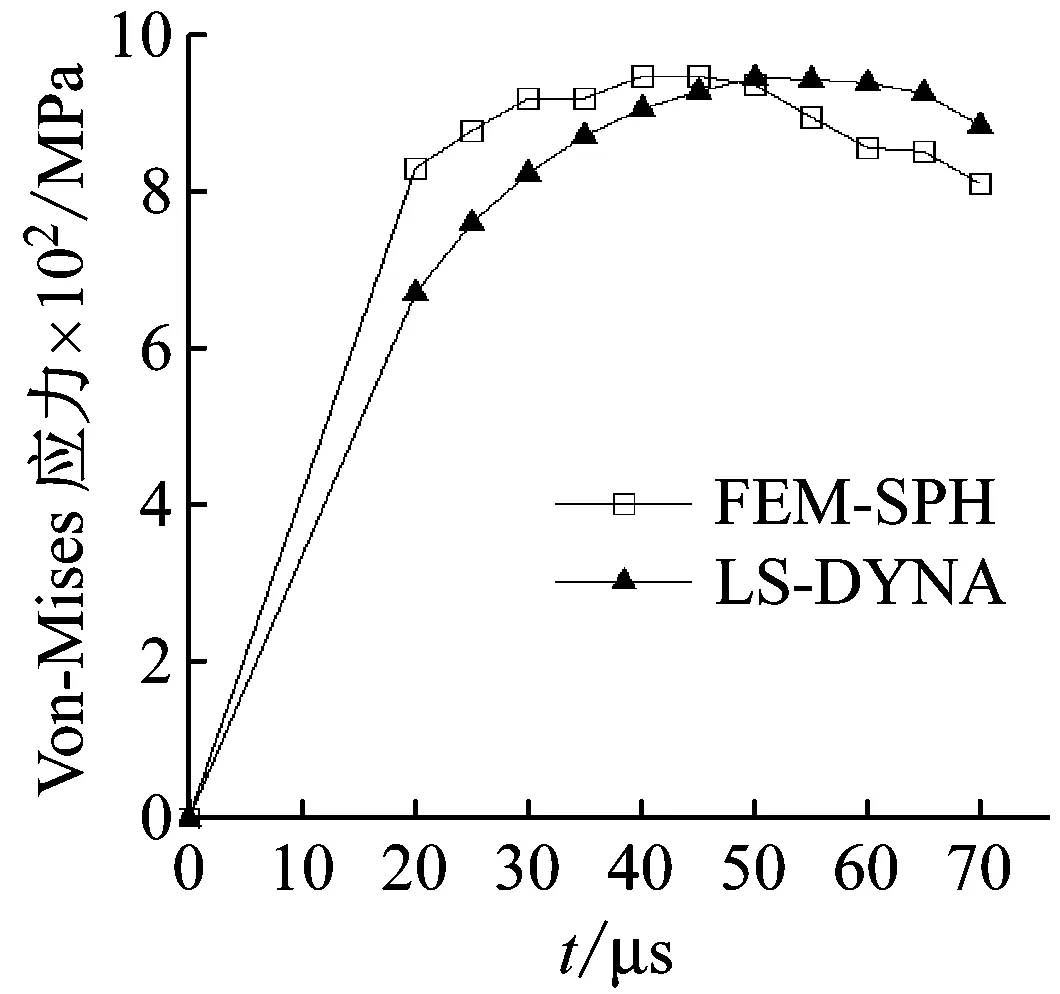
图5 A点的Von-Mises应力

3.2 600 g TNT炸药内爆加载下的厚壁容器

厚壁容器长度为1 000 mm，外径为93.5 mm，厚度为18.5 mm。预制孔长度为15 mm，宽度为2 mm。针对内爆载荷作用下的厚壁容器，文献[9]研究表明预制孔裂纹会沿着绝热剪切带方向扩展，此时将呈现绝热剪切为主导的韧性断裂模式。图6所示为实验得到的最终形貌与FEM-SPH自适应耦合算法计算得到的结果的比较。从图中可以看出，采用FEM-SPH自适应耦合算法模拟结果与实验得到的孔口破坏形貌有一定差别，但基本能反应出绝热剪切破坏。表5中进一步比较了实验、FEM-SPH自适应耦合算法与ALE算法计算得到的鼓包半径、收缩长度、孔口的宽度和剪切角，从表中可以看出FEM-SPH自适应耦合算法与ALE算法模拟结果具有较好的一致性，并且与实验获得的剪切破坏角度吻合较好。表5中数值模拟计算得到的孔端点距离与实验结果有较大差距，这是由于含预制孔容器在内爆加载下金属材料存在断裂破坏，这部分理论在本构方程描述中还有待进一步完善。另外，ALE算法得到的孔口的宽度也与ALE界面追踪算法的精度有关，两种数值模拟方法的结果也仅是定性的比较验证FEM-SPH模型的合理性。

(a)实验结果(b)FEM-SPH模型计算结果

图6 厚壁容器实验和数值模拟获得的最终形貌

Fig.6 The final morphology obtained by the experiment and numerical simulation for the thick-walled vessel

论文为了进一步分析FEM-SPH自适应耦合算法模拟内爆问题的有效性，选取A1点的Von-Mises应力值对FEM-SPH自适应耦合算法与ALE算法进行比较研究，A1点的位置示意如图3(c)所示。由数值模拟结果可知，A1点Von-Mises应力值在100 μs左右达到最大值，所以选取0～120 μs时间段进行研究。图7所示为FEM-SPH自适应耦合算法以及ALE算法得到的A1点在0～120 μs的Von-Mises应力。从图7中可以看出，由FEM-SPH自适应耦合算法得到的A1点的Von-Mises应力值与LS-DYNA中的ALE算法得到结果吻合较好。本模型计算结果进一步阐述了FEM-SPH自适应耦合算法模拟内爆厚壁容器爆炸响应的合理性。

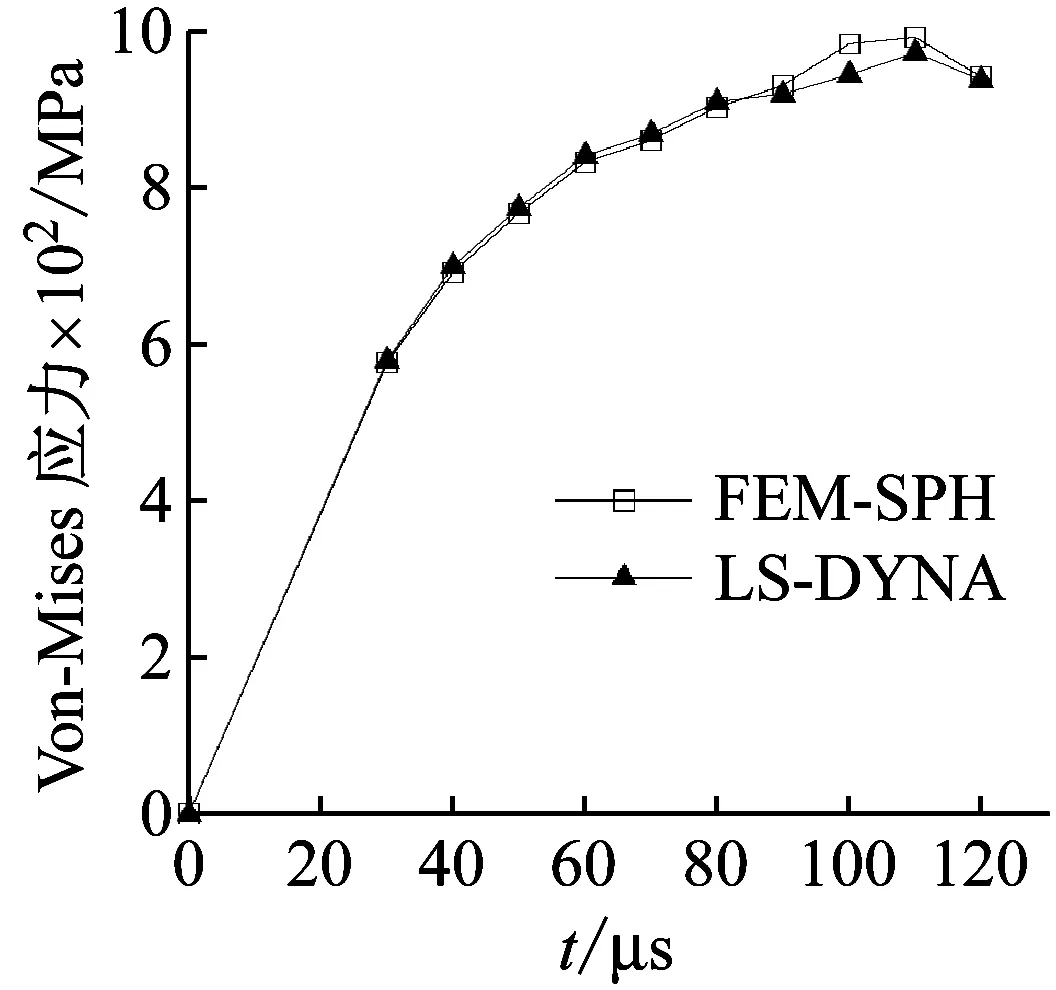
图7 A1点的Von-Mises应力

表4 薄壁容器实验及数值模拟得到的最大鼓包半径、收缩长度、孔口宽度及长度

表5厚壁容器实验及数值模拟得到的最大鼓包半径、收缩长度、孔口的宽度和剪切角

Tab.5Themaximumbulgingradius,finallength,widthandshearangleoftheholeobtainedbytheexperimentandnumericalsimulationsforthethick-walledvessel

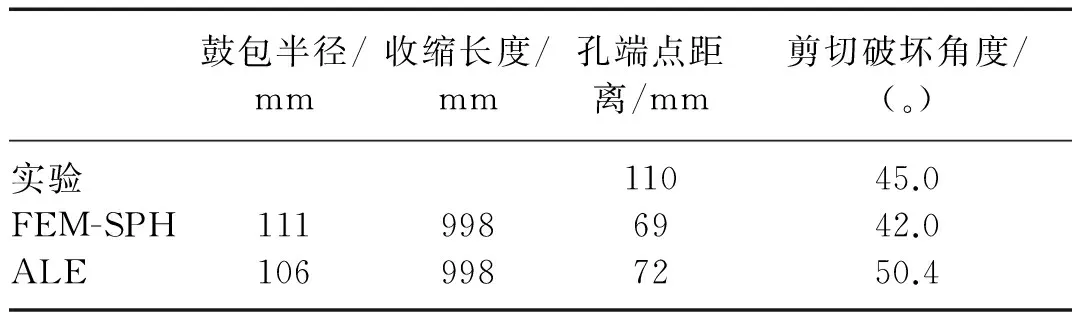
鼓包半径/mm收缩长度/mm孔端点距离/mm剪切破坏角度/(。)实验FEM-SPHALE111106998998110697245.042.050.4

4 容器内介质的动态响应

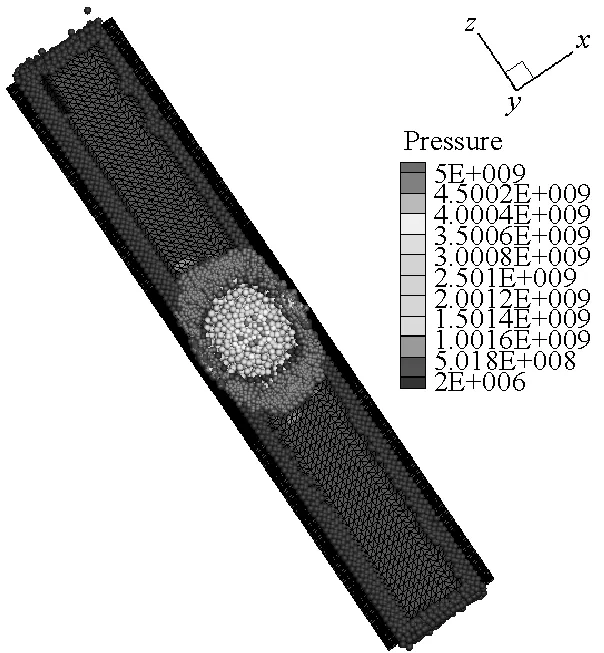
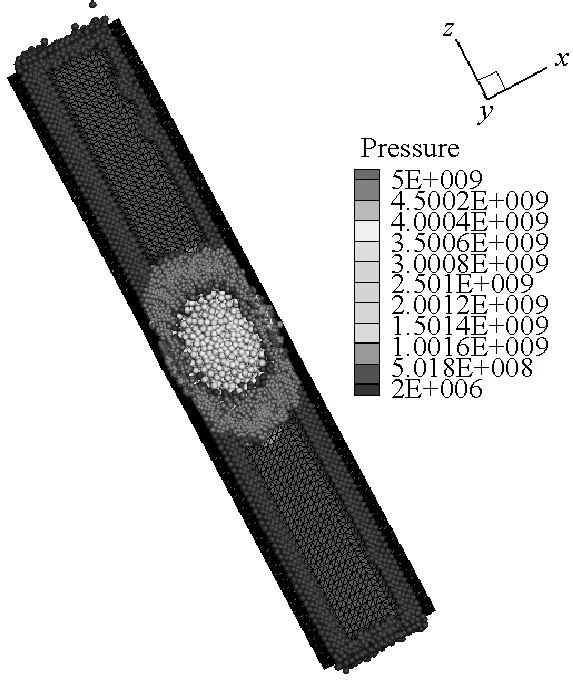
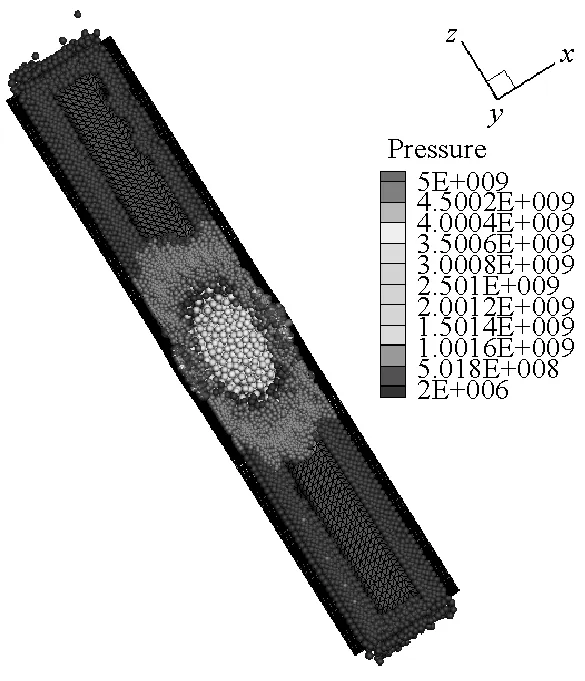
在炸药与靶体距离较近或者嵌入靶体内部的情况下，FEM-SPH自适应耦合算法模拟爆炸问题一般都忽略炸药周围空气对爆炸毁伤效应的影响。由于内爆容器的结构特点，空气介质会对容器的爆炸毁伤效应产生显著影响。因此，本文在前面模型计算中，考虑了空气的影响，并且初始模型全部采用单元进行离散，充分利用FEM计算效率高的特点。计算过程中，将大变形处的单元自动转化为SPH粒子，再利用SPH方法模拟大变形计算精度高、无网格依赖的特点进行模拟计算。图8给出了厚壁容器内70 μs前炸药和空气介质的离

散分布。从图中可以看出炸药和空气介质单元转化为SPH粒子的过程，并且容器内壁处由于接触力的作用，使得单元更先转化为SPH粒子。

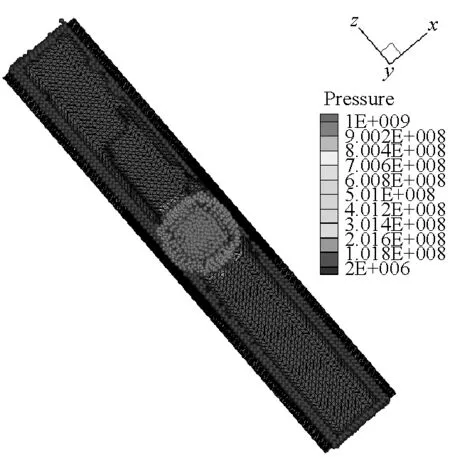
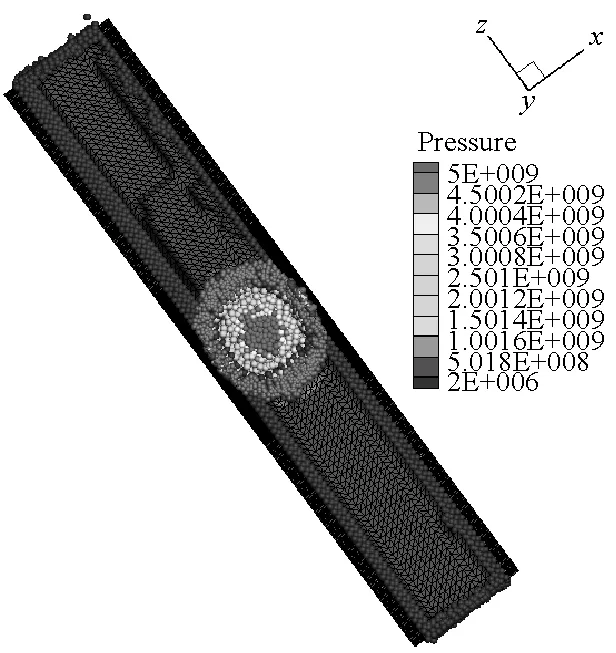
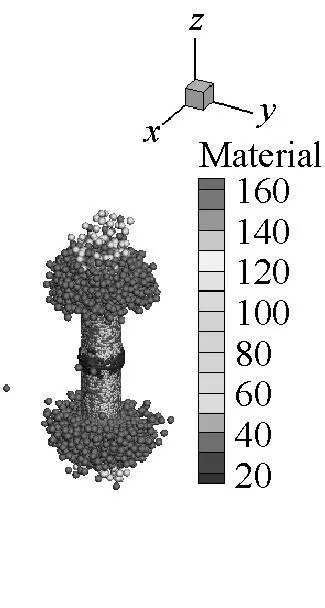
SPH方法作为一种具有无网格性质和拉格朗日性质的粒子法，研究对象的运动历程能够很自然地被捕获，可以很好地描述容器内部空气介质的爆轰变化过程，能够更方便描述爆轰过程对于周围环境的影响。本文薄壁容器和厚壁容器在爆炸载荷作用下内部介质的运动历程分别如图9和图10所示。从图9和图10中可以看出，由于厚壁容器的长度是薄壁容器长度的4倍，尽管厚壁容器内的炸药药量增加了，但是空气从厚壁容器的两个端口喷出的时间还是滞后，并且模拟结果中可以明显看到空气粒子从容器预制孔中喷出。

图11和12给出了薄壁容器和厚壁容器内测点的压力曲线，图中A2和A3点距各自炸药中心的距离与炸药中心到容器壁的距离一致。从图中可以看出，TNT炸药在空气中形成压力脉冲的时间为微秒级，由于厚壁容器内的炸药药量更大，使得其压力脉冲峰值更高，脉冲持续时间更长。薄壁容器测点A2处的压力峰值为220 MPa，压力脉冲持续时间约为40 μs。厚壁容器测点A3处的压力峰值为420 MPa，压力脉冲持续时间约为60 μs。

(a) t=15 μs

(b) t=20 μs

(c) t=25 μs

(d) t=30 μs

(e) t=40 μs

(a) t=20 μs

(b) t=40 μs

(c) t=60 μs

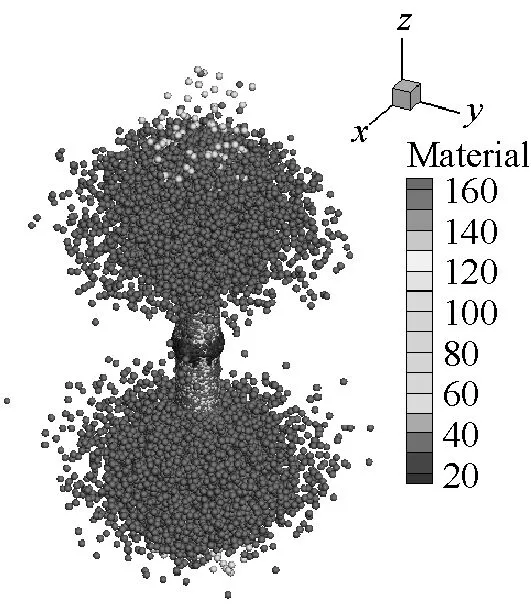
(d) t=100 μs

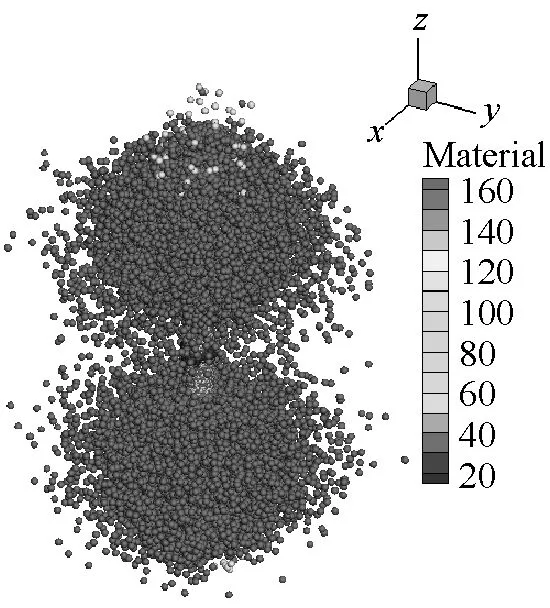
(e) t=150 μs

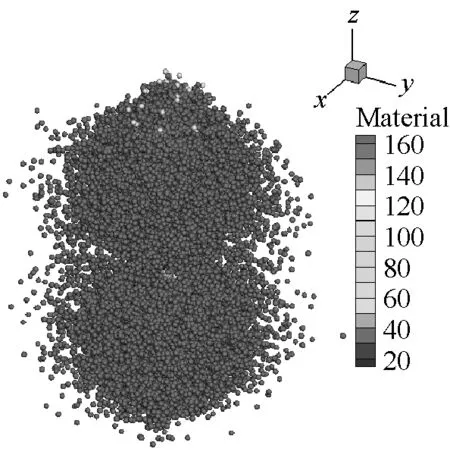
(f) t=300 μs

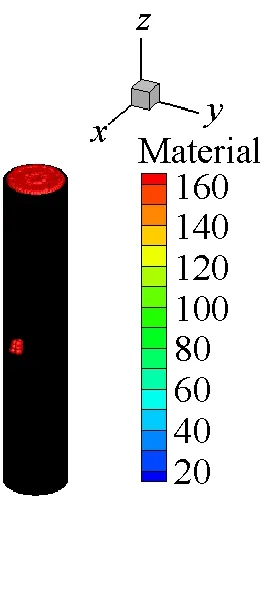
(a) t=20 μs

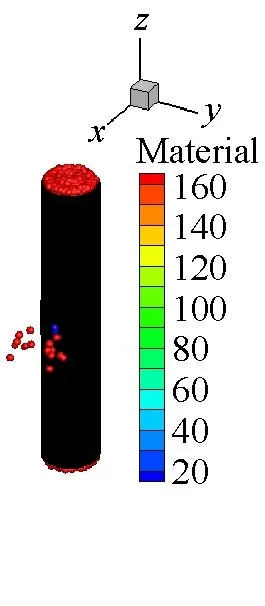
(b) t=40 μs

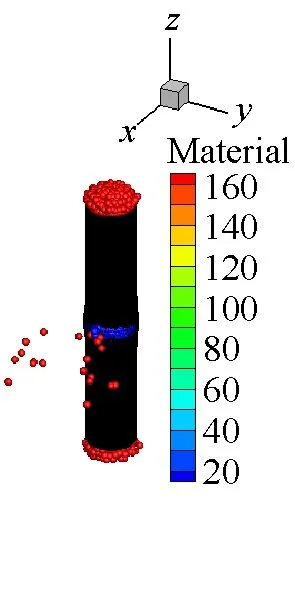
(c) t=70 μs

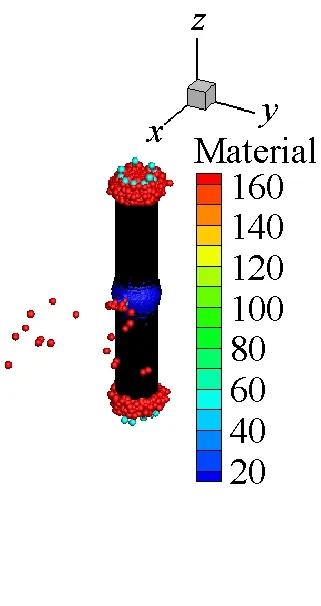
(d) t=100 μs

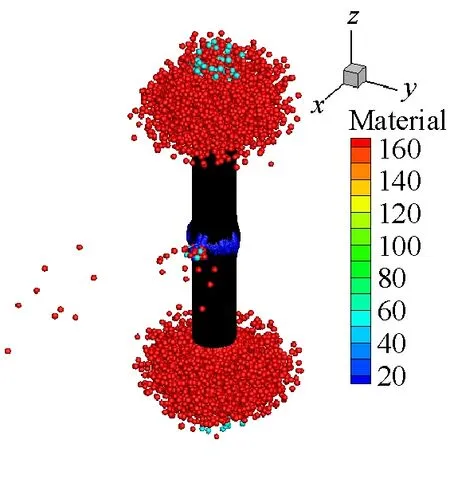
(e) t=150 μs

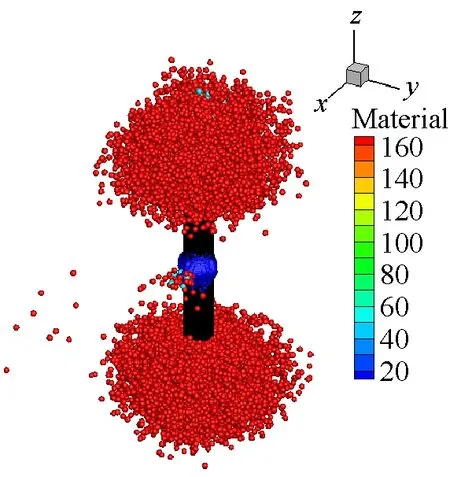
(f) t=200 μs

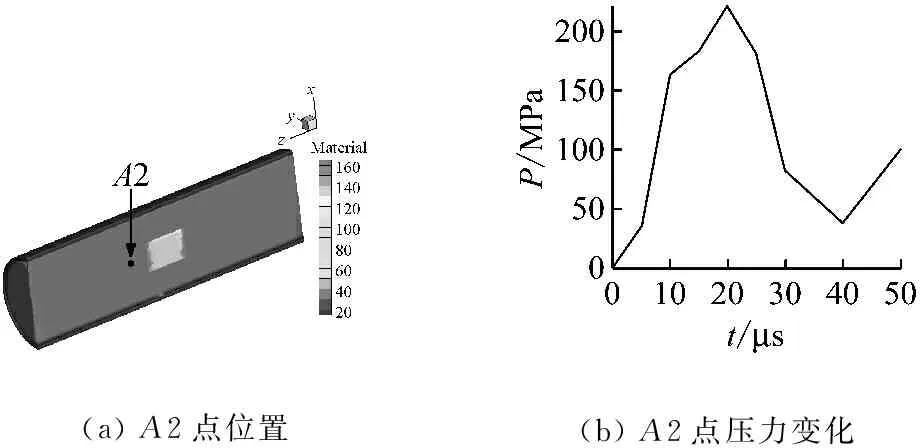
(a)A2点位置(b)A2点压力变化

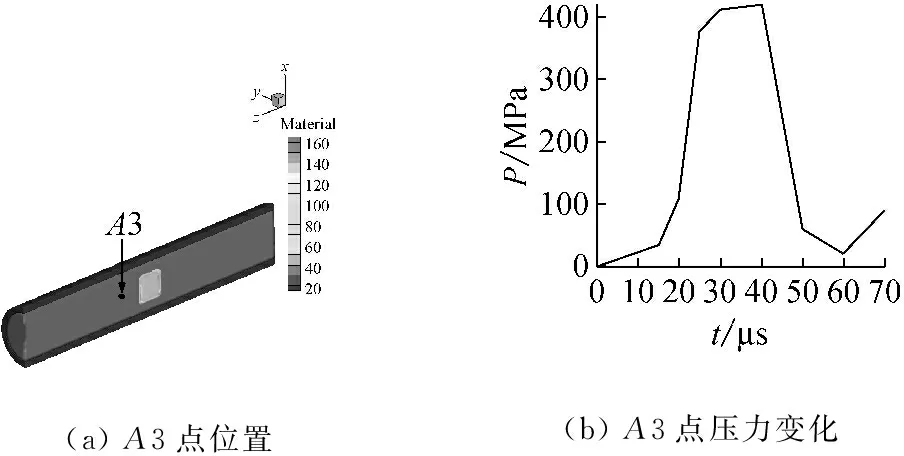
图11 薄壁容器内测点A2处的压力变化

图12 厚壁容器内测点A3处的压力变化

Fig.12 Pressure curve of pointA3 in the thick-walled vessel

5 结 论

本文建模过程中考虑空气的影响，采用三维FEM-SPH自适应耦合算法对不同药量下不同厚度内爆容器的爆炸响应过程进行了数值模拟。通过与实验及LS-DYNA软件中ALE算法的对比，表明FEM-SPH自适应耦合算法能够有效再现带预制孔内爆容器的爆炸鼓包过程和开孔损伤破坏过程。FEM-SPH自适应耦合算法可为容器内爆载荷作用下的动态响应提供有效的模拟计算途径。

论文研究给出了有限单元转化为SPH粒子的过程，表明接触界面处的单元更先转化为粒子。并且单元转化为SPH粒子后，SPH方法可以较容易的捕获内爆容器内炸药和空气介质的运动过程，获得容器内测量点的压力脉冲。论文研究结果表明，本文模型模拟结果符合内爆容器的规律特征，可为内爆容器研究提供参考。

参 考 文 献

[1] 胡八一, 周刚, 郑津洋,等. 爆炸容器研究及应用最新进展评述[C]// 压力容器先进技术-第七届全国压力容器学术会议论文集. 无锡：中国机械工程学会，2009.

[2] LIU M B, LIU G R, ZONG Z, et al. Computer simulation of high explosive explosion using smoothed particle hydrodynamics methodology[J]. Computers & Fluids, 2003, 32(3):305-322.

[3] JOHNSON G R, STRYK R A. Conversion of 3D distorted elements into meshless particles during dynamic deformation[J]. International Journal of Impact Engineering, 2003, 28(9): 947-966.

[4] JOHNSON G R. Numerical algorithms and material models for high-velocity impact computations[J]. International Journal of Impact Engineering, 2011, 38(6): 456-472.

[5] 王吉, 王肖钧, 卞梁. 光滑粒子法与有限元的耦合算法及其在冲击动力学中的应用[J]. 爆炸与冲击, 2008, 27(6):522-528.

WANG Ji, WANG Xiaojun, BIAN Liang. Linking of smoothed particle hydrodynamics method to standard finite element method and its application in impact dynamics[J]. Explosion and Shock Waves, 2008, 27 (6): 522-528.

[6] 胡德安, 孙占华, 朱婷. 三维自适应FE-SPH耦合算法在多层间隔金属靶侵彻问题中的应用[J]. 爆炸与冲击, 2015, 35(3):416-422.

HU Dean, SUN Zhanhua, ZHU Ting. Application of 3D FE-SPH adaptive coupling algorithm to penetration analysis of spaced multi-layered metallic targets[J]. Explosion and Shock Waves, 2015, 35(3): 416-422.

[7] MA L, HU Y, ZHENG J,et al. Failure analysis for cylindrical explosion containment vessels[J]. Engineering Failure Analysis, 2010, 17(5):1221-1229.

[8] MA L, XIN J, HU Y, et al. Ductile and brittle failure assessment of containment vessels subjected to internal blast loading[J]. International Journal of Impact Engineering, 2013, 52:28-36.

[9] 辛健, 马利, 胡洋,等. 内爆载荷作用下不锈钢圆柱壳的断裂失效分析[J]. 压力容器, 2013, 30(2):66-72.

XIN Jian, MA Li, HU Yang, et al. Fracture analysis of stainless steel tube under internal blasting loading[J]. Pressure Vessel Technology, 2013, 30(2): 66-72.

[10] LIU G R, LIU M B. Smoothed particle hydrodynamics: a meshfree particle method[M]. Hefei:World Scientific, 2003: 298-300.

[11] 杨秀敏. 爆炸冲击现象数值模拟[M]. 北京：中国科学技术大学出版社, 2010.

[12] JOHNSON G R. Linking of lagrangian particle methods to standard finite element methods for high velocity impact simulations[J]. Nuclear Engineering and Design, 1994, 150(2/3): 265-274.

[13] JOHNSON G R, STRYK R A. Symmetric contact and sliding interface algorithms for intense impulsive loading computations[J]. Computer Methods in Applied Mechanics & Engineering, 2001, 190(35):4531-4549.

[14] JOHNSON G R, STRYK R A, BEISSEL S R, et al. An algorithm to automatically convert distorted finite elements into meshless particles during dynamic deformation[J]. International Journal of Impact Engineering, 2002, 27(10):997-1013.

[15] CAMPBELL J, VIGNJEVIC R, LIBERSKY L. A contact algorithm for smoothed particle hydrodynamics[J]. Computer Methods in Applied Mechanics & Engineering, 2000, 184(1):49-65.

[16] LINDHOLM U S, JOHNSON G R. Strain-rate effects in metals at large shear strains[J]. Springer US, 1983: 61-79.

[17] 周光坰. 流体力学. 上册[M]. 北京：高等教育出版社, 2000.

[18] 胡八一, 柏劲松, 张明,等. 真实爆炸容器壳体动力响应的强度分析[J]. 应用力学学报, 2001, 18(3):91-95.

HU Bayi, BAI Jinsong, ZHANG Ming, et al. The dynamic response analysis of a real explosion-container vessel[J]. Chinese Journal of Applied Mechanics, 2001, 18 (3): 91-95.