基于性能的耐久性损伤RC构件时变抗震设计方法研究

梁 岩, 李 杰, 罗小勇, 陈 淮

(1.郑州大学 土木工程学院，郑州 450001；2.中南大学 土木工程学院，长沙 410075)

钢筋混凝土结构在长期使用过程中，受环境及荷载的影响，材料的力学性能将随服役年限的延长而发生退化，进而导致抗震性能降低。日本阪神地震及汶川地震震害调查表明：建造年代越久远的结构一般震害较严重，其原因除了早期设计不尽完善之外，就是恶劣环境引起结构损伤的累积降低了结构抗震性能[1]。地震引起的建筑物破坏的主要原因一方面是结构在长期使用过程中，由于材料老化、不利环境及使用不当等造成耐久性损伤，这种损伤积累直接导致了结构承载力下降、耐久性降低、抗震性能退化[2]；另一方面则是由于现行抗震计算理论和规范还存在着不足之处[3]。随着我国经济水平的提高，对建筑抗震设计要求也越来越高，以混凝土结构规范为例，结构的设计安全水平和安全储备从74规范以后逐渐提高，如表1所示。

地震中建筑结构的倒塌主要是由于结构的耗能能力差和塑性变形能力不满足所需的变形要求，基于承载力的设计不能保证结构达到预期的塑性变形或延性要求，而采用基于性能的设计方法可以达到此目的[4]。因此，考虑耐久性退化影响因素，采用基于性能的设计方法对结构或构件抗震设计是必要的。目前国内外对钢筋混凝土构件或结构的抗震设计中还未涉及耐久性要求，耐久性设计中也未设计抗震的要求。

结构抗震性能随着使用年限的延长发生降低，但另一方面，随着结构后续使用年限的减少，基于设计基准期的地震作用也有所降低。抗震设计时，如何共同考虑二者的影响，目前还未见相关研究报道。本文是在作者已有研究成果[6-10]的基础上，采用基于性能设计方法，考虑典型耐久性环境的影响，以及随着后续使用年限的减少后基于设计基准期的地震作用的降低，探讨基于性能的耐久性损伤钢筋混凝土构件时变抗震设计方法。

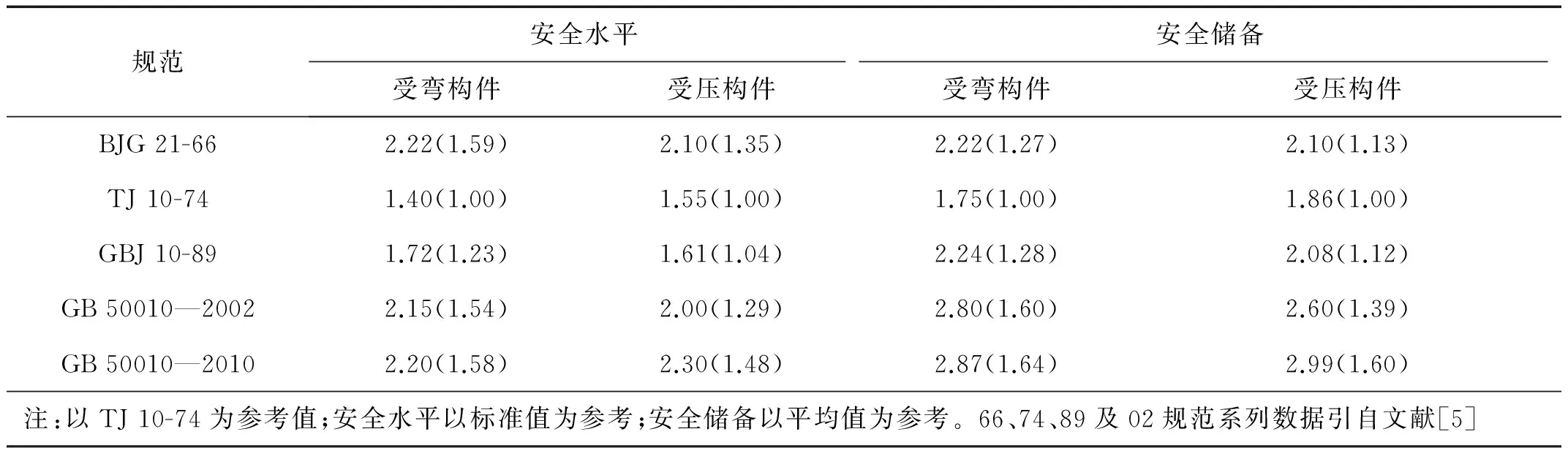
表1 混凝土结构设计规范安全性能对比

1 基于设计基准期的时变地震作用

设计使用年限内耐久性损伤的结构抗震设计，应考虑基于设计基准期的时变地震作用。结构的设计基准期是与评估基准期相对应，后续使用期内小震烈度对应的重现期，对某一具体结构来说，它应是一个随后续使用期变化的量[11]。

地震重现期TR为设计基准期T和超越概率P的函数[12]

TR=1/[1-(1-P)1/T]

(1)

对于不同的基本烈度区，地震重现期为X的设防烈度I可以表示为[13]

I=a(logX)2+blogX+c

(2)

式中:a，b，c为常数，对于不同基本烈度区取值不同。

强度提高系数k是一个与典型环境下使用年限内配箍特征值λv有关的量，随着λv的增加而增大。将k计算式(9)代入式(13)求解λv将使计算变得复杂，不易应用。当λv在0.05～0.2内时(这个范围覆盖了工程常规的配箍特征值)，k变化范围为1.12～1.44，简化计算时，取k=1.4，则式(13)可简化为

峰值加速度A与地震烈度I之间的统计关系式为[14]

2.7.1 疟原虫感染对按蚊吸血的影响 按蚊叮吸正常对照小鼠和感染疟原虫小鼠的吸血率显示，二者差异有统计学意义（P＜0.05）。其中，叮吸正常对照组小鼠按蚊的7.8 min吸血率维持在42%左右，而叮吸疟原虫感染小鼠按蚊的吸血率可高达93%左右，见图6A。目视法统计的吸血率结果与称重法的计算结果一致，见图6B。

A=10Ilg 2-0.01(cm/s2)

(3)

评估地震作用影响系数最大值αmax与地震烈度的关系可表示为

αmax=10Ilg 2-2.755

(4)

根据以上原理，考虑后续使用年限内地震发生的可能性，以抗震设防烈度7度为例，随着后续使用年限的不同，评估烈度、水平地震影响系数最大值及峰值加速度的时变性如图1所示。

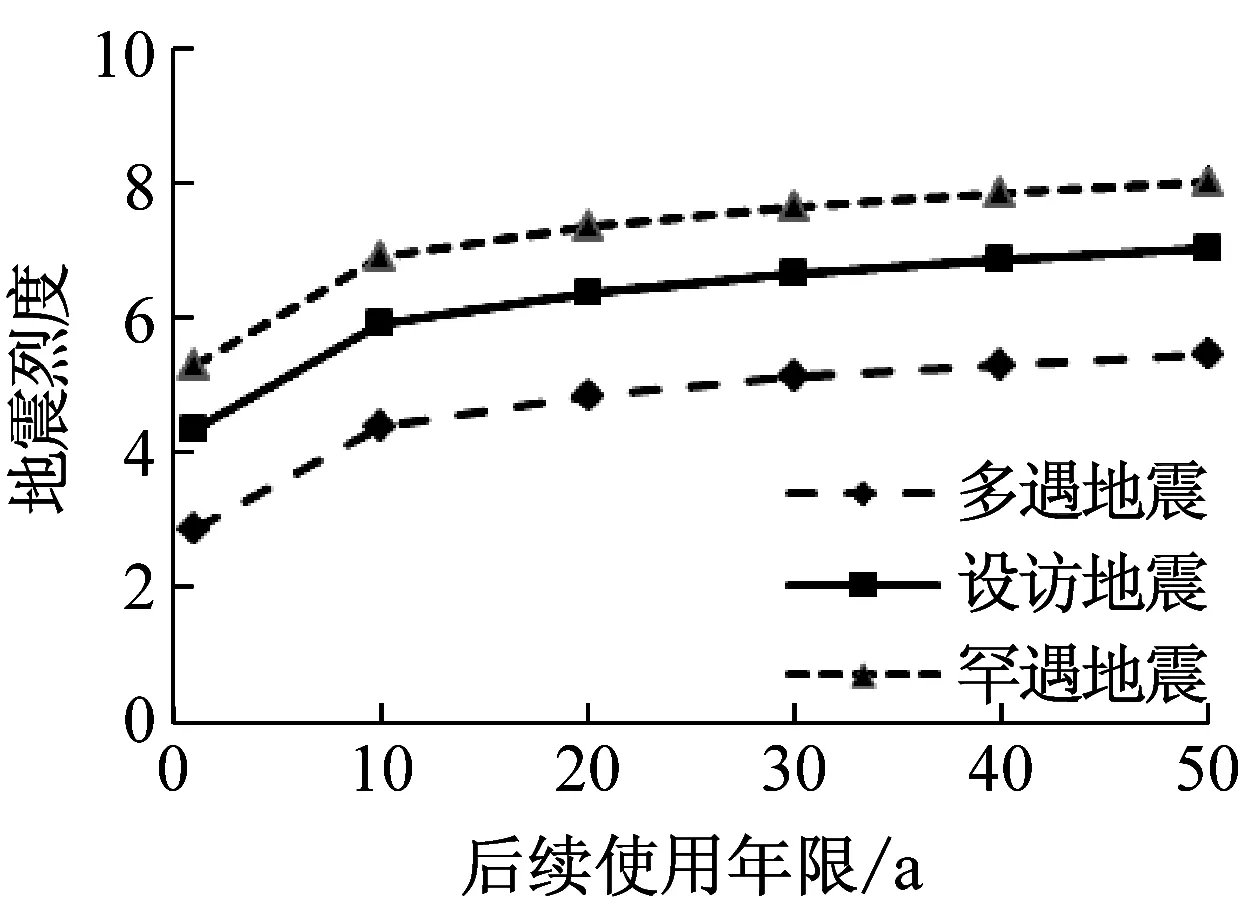
(a)地震烈度

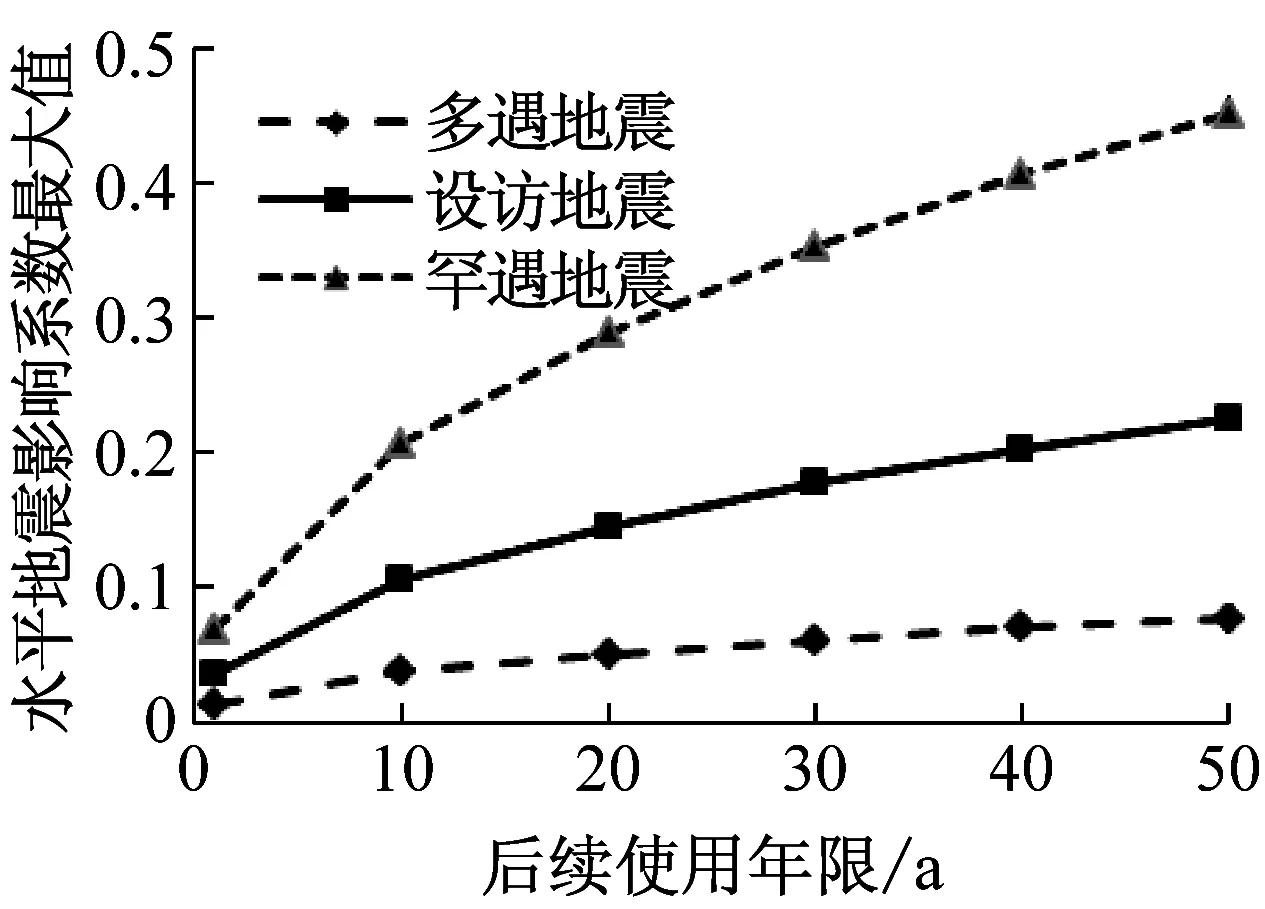
(b)水平地震影响系数最大值

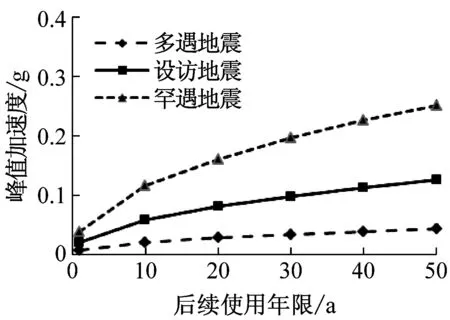
(c)峰值加速度

2 基于性能的耐久性环境下构件时变抗震性能设计方法

钢筋混凝土构件的变形能力主要取决于截面塑性转动量，而影响截面塑性转动量的主要因素是截面的变形能力和塑性铰的长度。塑性铰长度可根据现有研究成果的经验公式确定，而截面的变形能力与混凝土力学性能及相对受压区高度ξ有关。箍筋约束作用可以有效改善混凝土延性，若能建立塑性铰区极限转动量θu或截面曲率延性μφ与相对受压区高度ξ及配箍特征值λv之间的定量关系，则可由变形的性能要求定量设计构件的配箍特征值，也可确定构件的变形能力，评估构件在指定变形需求下的性能状态。

2.1 典型耐久性环境下构件变形关系建立

以受弯构件为例，根据构件截面的曲率关系可得

εcu(E,T)=[xn(E,T)-a′]φu(E,T)

(5)

式中：E,T为典型耐久性环境及使用时间，各参数均为二者的函数；xn为受压区高度，xn=ξnh0；ξn为实际受压区高度系数；h0为截面有效高度；a′为箍筋内边缘到混凝土受压边缘的距离。

构件截面的曲率延性可表示为

φu(E,T)=μφ(E,T)φy(E,T)

(6)

式中：φu为典型环境下使用年限内截面极限曲率；φy为典型环境下使用年限内截面屈服曲率；μφ为典型环境下使用年限内截面曲率延性系数。

由表2可知，在随着使用年限的增长，时变目标曲率延性有所降低，但应箍筋配置应满足配箍特征值要求，从而才能保证构件的变形能力，使得结构具有良好抗震性能。

εcu(E,T)=0.004+

(7)

式中：ρv为典型环境下使用年限内体积配箍率；εsu为典型环境下使用年限内约束箍筋极限拉应变；fyh为典型环境下使用年限内箍筋屈服应力；fcc为典型环境下使用年限内约束混凝土峰值应力，由式(8)确定

fcc(E,T)=kfc0(E,T)

(8)

式中：fc0为典型环境下使用年限内无约束混凝土强度；k为约束混凝土强度提高系数，由式(9)确定

keλv(E,T)-1.254

(9)

式中：ke为矩形截面有效约束系数，取0.75；λv为典型环境下使用年限内配箍特征值，由式(10)确定

(10)

从偏于保守的设计角度出发，取式(16)的上限值代入式(14)，实际受压区高度系数ξn(E,T)≈ξβ(E,T)≈ξ(E,T)/β，并近似取h0与h相等，可使式(14)得以简化

(11)

若忽略式(5)中的a′，则

εcu(E,T)=xnφu(E,T)=

ξn(E,T)h0μφ(E,T)φy(E,T)

(12)

代入式(11)可得

文章认为不合理低价游是旅游者、旅行社和相关管理部门故意无视的结果。只有消除事前的故意无视，事后的默认补偿才能得以解决。如何消除故意无视呢？

λv(E,T)=

(13)

说真的，一个品牌的成功，因素肯定是多方面的，从品质到坚持，从外部环境到历史的机遇，从优秀的团队到强大的执行力，从策略到战略……如果作为一个商业案例来分析，没有个几十页，根本无法稍微深入点讲清楚。但有时候，一些细节和侧面也可见一斑。

λv(E,T)=

(14)

由式(14)可得典型环境下使用年限内构件截面配箍特征值与相对受压区高度及曲率延性的λv-ξn-μφ关系。对于给定曲率延性μφ，确定受压区高度系数ξn后就可计算所需的λv，进而确定所需的箍筋。

文献[17]表示：可采用无约束截面在极限状态下的受压区高度可以近似代替约束截面在任意指定延性下的受压区高度，可采用无约束截面的屈服曲率可近似代替约束截面的屈服曲率。ξβ(E,T)为矩形应力图形计算的受压区高度系数，与规范的等效矩形应力受压区高度系数ξ关系见式(15)，ξ取0.8。

(15)

由图3及图4可知：随着使用年限的增长，构件截面曲率延性及极限转动量逐渐减小，构件变形能力降低。若考虑耐久性退化，为保证典型环境下使用年限内构件的抗震性能，则应根据使用年限及典型的耐久性环境对规范规定的构件抗震性能设计要求做适当调整。

Priestley[18]指出钢筋混凝土截面的屈服曲率与截面配筋基本无关，而与截面高度和受拉钢筋屈服应变有关，提出的混凝土梁截面屈服曲率经验式(16)。

(16)

式中：εsy(E,T)为典型环境下使用年限内纵筋屈服应变；hb为构件截面高度。

其中，10%是Priestley考虑到大多数范围内此公式计算的截面屈服曲率与实际截面的φby偏差。

美国专利链接制度实施几十年以来，随着第IV段专利挑战数量的增加，因此而引发的诉讼数量也随之增加。据统计，1992-2001年10年间，美国共有75件针对首个第IV段专利声明提起的专利诉讼，每年平均仅有7.5件；⑬ 同注释⑫。而在2003年至2009年7年间就有238件此类诉讼，每年平均达34件，且每年的诉讼量逐年上升。⑭ RBC Capital Markets Corp. Analyzing Litigation Success Rates，January 15, 2010.

将式(10)代入式(7)，整理可得

毛先舒从“含蓄为正”出发，在《竟陵诗解驳议》中批评钟惺“指义浅率，展卷即通”，不满“竟陵派”的“高谈性灵”“一往欲尽”，在评价杜甫的诗句“文章有神交有道”时显出不满，毛先舒批评道：“虽云深老，且起有势，却是露句，宋人宗此等失足耳。”而在《诗辩坻》第三卷中对张若虚的《春江花月夜》给予很高的评价：“不著粉泽，自有腴姿，而缠绵蕴藉，一意萦纡，调法出没，令人不测，殆化工之笔哉！”

λv(E,T)=

COPD急性加重期患者因气道黏液分泌亢进,气道分泌物增加,加上患者心肺功能差、咳嗽无力、痰液黏稠,易堵塞呼吸道,引起感染,诱发呼吸衰竭或心力衰竭等并发症,危及患者生命,积极排痰是治疗COPD急性加重期的关键。

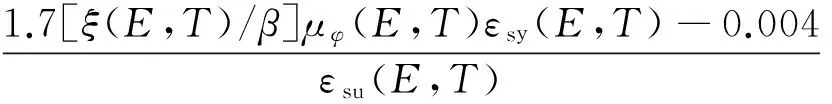
根据规范要求，以长沙典型的耐久性环境下一级框架为例，截面尺寸为350 mm×800 mm，按规范规定的配箍特征值λbv及最小配筋率设计，跨中箍筋HPB300为Φ8@200，受拉钢筋HPB335配置3Φ22，受压钢筋HPB335配置2Φ14，混凝土取C30，按本文方法计算规范值所达到的极限变形能力。将计算得到的曲率延性要求及构件端部塑性极限转动量见图3及图4。

(17)

至此建立了典型环境下使用年限内构件配箍特征值的简化计算式(17)。据此可仅由矩形应力图法得到ξ(E,T)，设定目标曲率延性μφ(E,T)，可计算典型环境下使用年限内配箍特征值λv(E,T)。

以长沙典型耐久性环境为例，构件截面取350 mm×800 mm，受拉钢筋9根直径为32 mm HPB400级钢筋，受压钢筋4根直径为22 mm HPB400级钢筋。地震中，构件发生延性破坏时，延性系数约为10～20，本文中目标曲率延性取15，设计使用年限为100年，根据以上方法该构件在设定目标曲率延性下变形能力设计见表2。

约束混凝土极限压应变εcu采用Paulay等[15]改进的Mander等[16]的计算公式

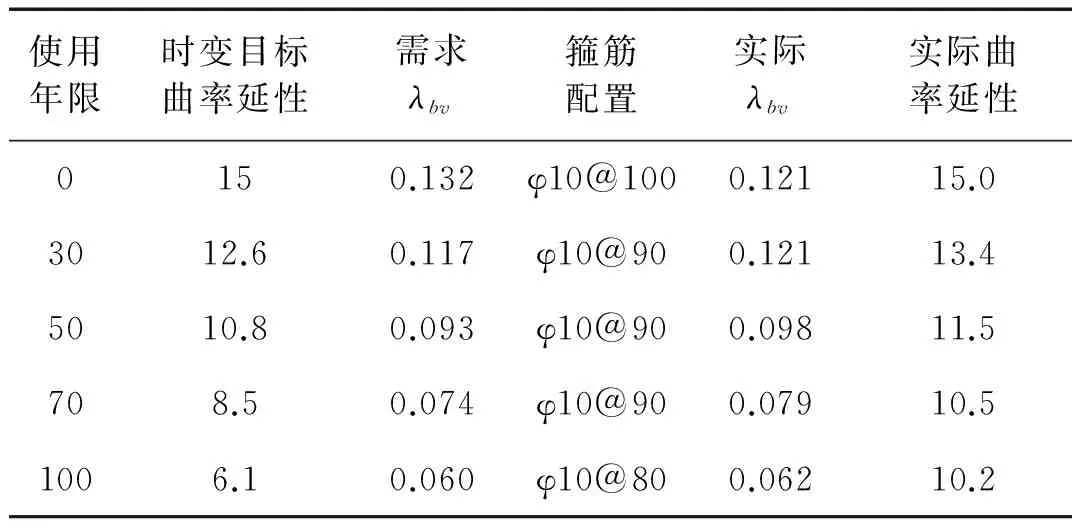
表2 构件变形能力设计

2.2 典型耐久性环境下构件基于性能设计

本文采用钢筋混凝土构件关键受力区域塑性铰区的变形来度量其破损状态，见式(19)

(18)

式中：θ为构件端部的塑性铰转动设计需求量；θu为构件端部塑性铰区极限转动量；DI为破损指标，具体值由性能要求设定。

构件端部的塑性铰长度l可取0.5h，根据性能要求所确定的构件端部典型环境下使用年限内目标曲率φu及目标曲率延性μφ为

(19)

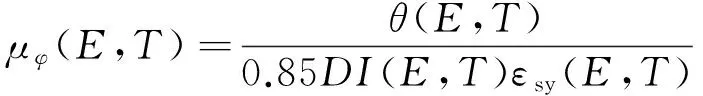
(20)

将式(19)和式(20)代入式(17)经整理得到

λv(E,T)=

教师在谈话过程中要给予学生足够的尊重，这种尊重最基本的表现便是倾听学生的诉说。教师要让学生将事件发生的经过以学生自己的角度进行讲述，让学生将自己心中的实际想法表达出来。教师对于学生的错误要帮助其进行分析和改正，而不能以训斥的和挖苦的方式对待学生。帮助学生改正和弥补错误是首要任务，话难听、脸难看的谈话对于学生来说毫无意义，只能够加深师生之间的对立，使本就叛逆心较强的学生与教师进行对抗。

(21)

式(21)为设计构件变形能力所需的构件端部塑性铰转动需求量θplb及性能要求破损指标DI的关系式，设计流程见图2。周定松等的计算结果表明：塑性铰转动量与受压区高度都相同时，不同性能目标下所需的约束箍筋用量差别较大，对于较高的性能要求，则需更多的约束箍筋，以满足设定性能目标对变形性能的要求。

以长沙典型耐久性环境为例，构件最大破损指标取0.8，相对受压区高度取0.2，塑性铰区转动需求量为0.01，根据以上方法该构件在设定目标性能下配箍设计见表3。

纳入标准：①实验室检查、影像学以及临床表现均符合急性扁桃体炎诊断标准；②患者知情同意并签署知情同意书。排除标准：①伴有急、危重疾病者；②先天性呼吸系统疾病、精神异常者；③入院前采用抗生素、抗病毒药物治疗者。

3 基于性能的耐久性环境下构件时变抗震性能设计要求

GB 50011—2011《建筑抗震设计规范》6.3.4条规定：沿梁全长顶面、底面的配筋，一、二级不应少于2Φ14，且分别不应小于梁顶面、底面两端纵向配筋中较大截面面积的1/4。GB 50011—2010《混凝土结构设计规范》抗震设计条文11.3.6条对框架梁的纵向受拉钢筋的配筋率作出了相应规定；11.3.9条对箍筋的面积配筋率ρsv亦作出了相应规定。

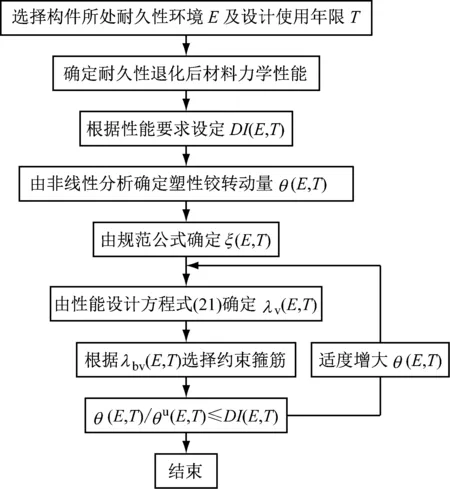
图2 耐久性退化构件基于性能设计流程

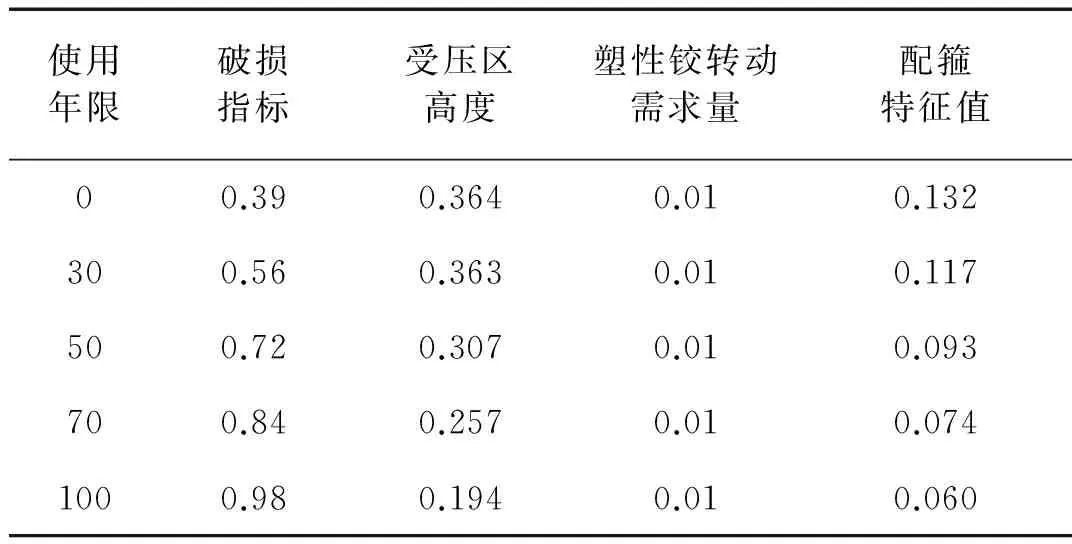
使用年限破损指标受压区高度塑性铰转动需求量配箍特征值00.390.3640.010.132300.560.3630.010.117500.720.3070.010.093700.840.2570.010.0741000.980.1940.010.060

同治六年(1867)三月,图库尔共收集了3000余人，四月，又收集3000余名溃兵，四月之后，又陆续收集4000余人，在近三个月时间里，共收集万余人之多。九月，又有部分塔尔巴哈台十苏木蒙古人西移，陆续至噶扎勒巴什淖尔一带。[注]中国边疆史地研究中心、中国第一历史档案馆合编：《清代新疆满文档案汇编》279，“同治五年四月十六日塔尔巴哈台领队大臣图库尔奏沥陈塔尔巴哈台城失陷情形折”，广西师范大学出版社，2012年，第421～422页。

应用x2检验比较整改前后的药品基数不合理，标识不清，无标识以及摆放不合理情况。搜集比较的数例为300例。

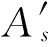
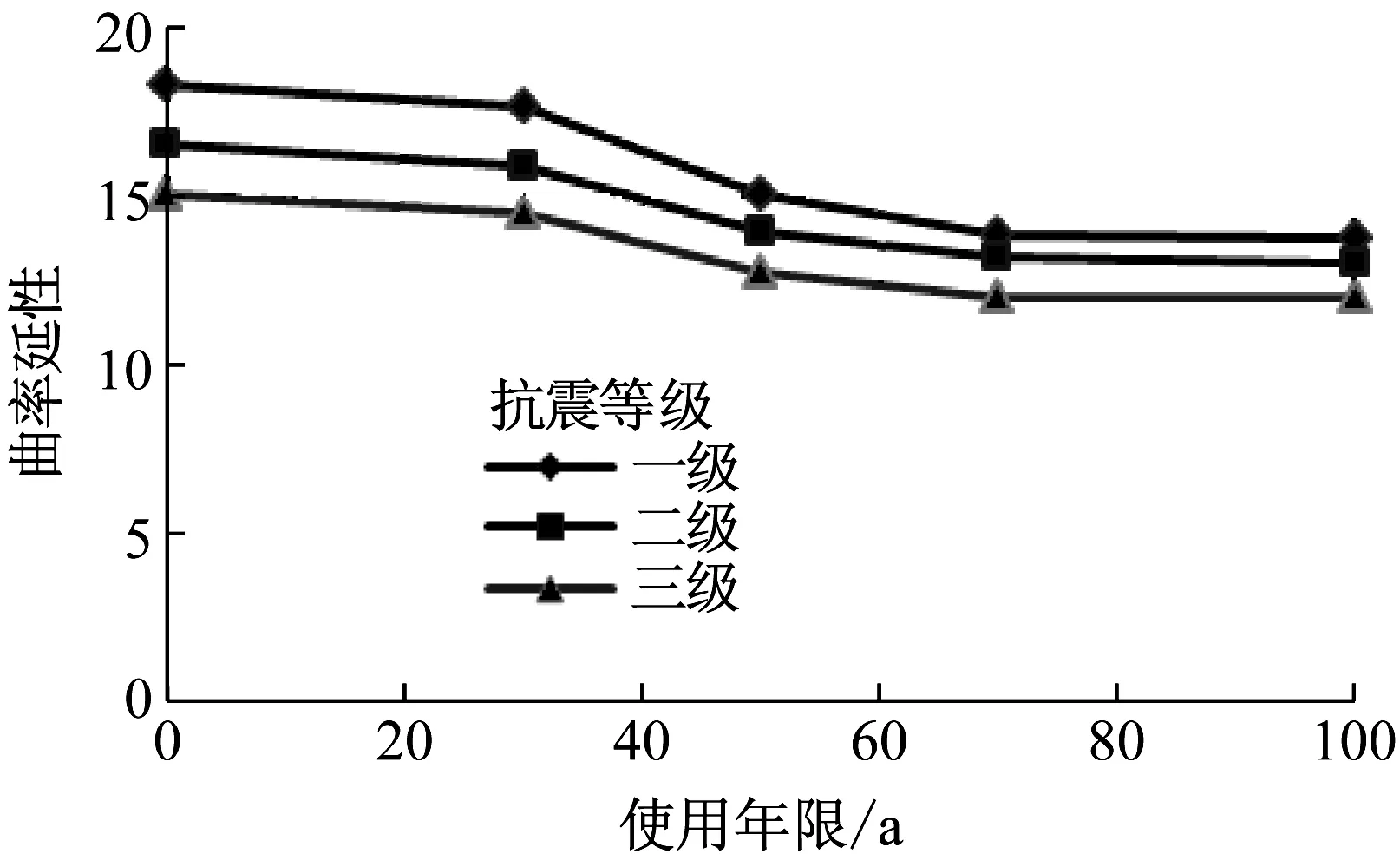
图3 曲率延性随使用年限变化

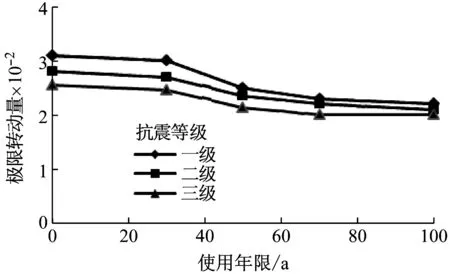
图4 极限转动量随使用年限变化

4 典型耐久性环境下钢筋混凝土构件的抗震设计建议

根据GB/T 50475—2008《混凝土结构耐久性设计规范》规定：“钢筋发生适量锈蚀的极限状态应为钢筋锈蚀发展导致混凝土构件表面开始出现顺筋裂缝，或钢筋截面的径向锈蚀深度达到0.1 mm”，根据作者研究结果，构件达到耐久性极限状态时，按箍筋与纵筋锈蚀程度计算，一般大气环境下，其使用年限分别为27年与44年；近海大气环境下，其使用年限分别为28年与39年。若以“钢筋发生适量锈蚀状态作为极限状态”，此处假设钢筋发生适量锈蚀时锈蚀率为10%，则构件达到耐久性极限状态时，按箍筋与纵筋锈蚀程度计算，一般大气环境下，其使用年限分别为34年与58年；近海大气环境下，其使用年限分别为32年与50年。换言之，箍筋锈蚀控制着结构构件的服役年限，文献[20]也体现了该类似结论。但另一方面，对钢筋混凝土构件抗震耐久性设计时也应考虑纵筋锈蚀导致的承载力下降所造成的不利影响。以未发生耐久性退化时构件曲率延性及极限转动量为标准，抗震设计最低限值提高系数为1，则建议设计使用年限内构件抗震设计最低限值提高系数计算见表4。其中：配筋率提高系数是根据钢筋随使用年限增长锈蚀率增大求得；配箍特征值提高系数是根据本文提出的基于性能的耐久性损伤钢筋混凝土构件时变抗震设计方法求得。

表4 抗震设计限值调整系数

由表4可知，构件使用年限内典型耐久性环境下，建议对规范限值进行修正，特别是配箍特征值限值应适当提高，从而保证构件的抗震性。以钢筋混凝土构件的相对受压区高度限值ξb为例，考虑耐久性环境及使用年限后，纵向受拉钢筋屈服与受压区混凝土破坏同时，发生时有屈服点的普通钢筋的钢筋混凝土构件的相对受压区高度限值ξb可按下列公式计算

(22)

式中：β1为系数，按GB 50011—2010《混凝土结构设计规范》6.2.6条计算；fy(E,T)为典型环境下，使用年限内钢筋屈服强度；Es(E,T)为典型环境下，使用年限内钢筋弹性模量；εcu(E,T)为典型环境下，使用年限内混凝土极限压应变；

权巍，赵云秀，韩成，等.基于立体图像感兴趣区域及对比度的舒适度评价模型[J].光子学报，2018，47(12)：1210002

以长沙典型耐久性环境为例，常用纵筋选用HRB335及HRB400，由上式及材料力学性能的劣化研究成果，可计算构件的相对受压区高度限值ξb随使用年限的变化趋势见图5。

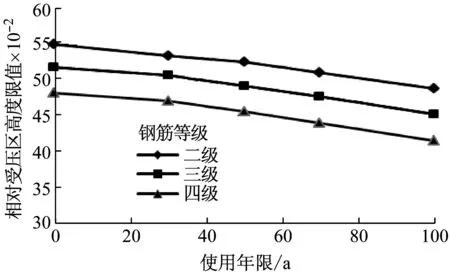
图5 配置不同等级钢筋的ξb变化趋势

由图5可知：一般大气环境下，规范规定的构件相对受压区高度限值应随设计使用年限的增长适当降低，从而保证构件的延性。

在全球化大背景下，企事业单位可能会面临新的形势、新的任务、新的机遇、新的挑战，要想在新环境下有出色的表现，在现代经济中占一席之地，完善单位内部控制是关键，进而制定出合理的内部控制建设方案。

根据GB 50011—2010《混凝土结构设计规范》抗震设计条文11.3.1条要求，考虑使用年限内典型耐久性环境的影响，抗震设计时，梁正截面受弯承载力计算中，计入纵向受压钢筋的梁端混凝土受压区高度，应符合下列要求：

一级抗震等级

x≤0.25μE,Th0

(23)

二、三级抗震等级

x≤0.35μE,Th0

(24)

式中：μE,T为构件延性退化比。

由式(23)及式(24)以一般大气环境为例，构件端部的相对受压区高度限值随使用年限的取值变化趋势见图6。由图6可知：典型环境内构件规范规定的相对受压区高度限值应随设计使用年限的延长适当降低，保证构件的延性，从而避免结构在地震中突然倒塌。

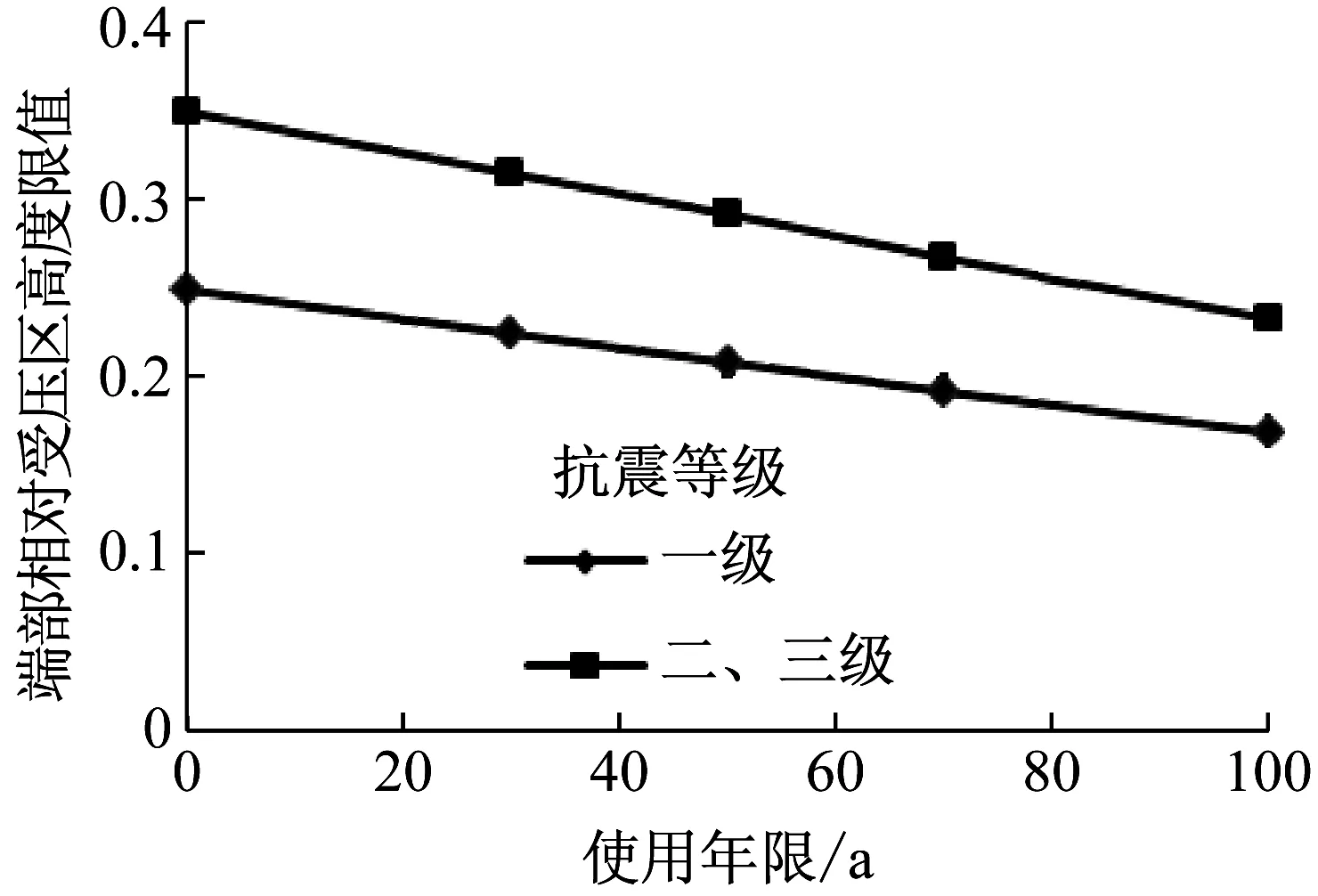
图6 不同抗震等级下的ξb变化趋势

随着使用年限的延长，钢筋锈蚀对构件抗震性能影响较大，是造成构件抗震耐久性退化的主要原因。钢筋锈蚀程度较大，主要是因为箍筋保护层厚度相对较小，加大保护层厚度可推迟钢筋开始锈蚀时间，降低使用年限内钢筋锈蚀率。GB 50011—2010《混凝土结构设计规范》从混凝土碳化、钢筋脱钝和锈蚀的耐久性角度考虑，修订后的保护层厚度比原规范有所加大。但是，对于构件承受拉应力时，加大保护层厚度易使混凝土在过早开裂，降低结构正常使用性能，导致结构不满足正常使用极限状态。因此，对构件抗震耐久性设计时，是否需要对混凝土保护层厚度进行调整，还有待进一步研究。

5 结 论

本文通过对基于性能的耐久性损伤钢筋混凝土构件时变抗震设计方法研究，主要结论如下：

(1)典型耐久性环境下，基于性能的钢筋混凝土构件抗震设计应对构件变形能力进行量化处理，由此建立了使用年限内典型耐久性环境下，构件破损指标、相对受压区高度、配箍特征值及曲率延性的量化关系式，可用于构件截面在目标曲率延性下的变形能力设计。并以实际构件为例，给出了典型环境下构件随使用年限的增长，在目标延性和破损指标下所需的箍筋配置计算方法。

(2)对耐久性退化钢筋混凝土结构的抗震性能评估，应考虑后续使用年限内的地震作用与基于设计基准期的地震作用有所不同，本文给出了随着后续使用年限的不同，评估烈度、水平地震影响系数最大值及峰值加速度等地震作用时变性。

(3)对钢筋混凝土构件抗震耐久性设计时，应根据使用年限及耐久性环境，通过性能目标来调整构件设计要求。建议对规范配箍特征值、最小配筋率及相对界限受压区高度等抗震指标进行调整，从而保证结构的抗震性能。以一般大气环境为例，给出了典型耐久性环境下，构件抗震耐久性设计时的最小配筋率和最小配箍率调整系数，以及不同抗震等级下的相对受压区高度在不同设计使用年限内的限值要求。

RESRAD-BIOTA程序由美国能源部开发，获得核管会批准，是一个用于估算水生和陆地生物辐射剂量的模型软件，目前其数据库中涵盖46种放射性核素。该软件对多种有机体进行了评价，来开发默认曝露参数值。如果用户输入相应的曝露参数的话，RESRAD-BIOTA还有能力评价特定有机体的辐射曝露。该模型采用了三级筛选的方法进行生物辐射影响的评价。

(4)不同地方的断层情况，经地震危险性概率分析得到的地震PGA超越概率分布函数也不同，由于缺乏地震危险性概率分析得到的基础数据，因此更合理的地震重现期与设防烈度的关系还有待进一步分析确定；另外，钢筋混凝土构件配筋率的取值受多种综合因素的影响，不是为了仅保证延性确定的，本文研究内容为耐久性损伤钢筋混凝土构件时变抗震设计提供了一种思路，但定量的设计过程还有待进一步研究。

[1] 杨光，沈繁銮.日本阪神地震灾害的一些调查统计数据[J].华南地震,2005,25(1):83-86.

YANG Guang,SHEN Fanluan. Establishment survey data of Japan hanshin earthquake disasters[J]. South China Journal of Selsmology,2005, 25(1):83-86.

[2] CAIMAS J, PLIZZARI G, DU Y. Mechanical properties of corrosion-damaged reinforcement[J]. ACI Materials Journal, 2005,102(4):256-264.

[3] 金伟良,夏晋.汶川地震中混凝土结构的耐久性的思考[C]∥汶川地震建筑震害调查与灾后重建分析报告.北京：中国建筑工业出版社，2008：326-334.

[4] 季静，肖启艳，黄超，等．基于性能的钢筋混凝土剪力墙受弯破坏变形限值的研究[J]．建筑结构学报，2010，31(9)：35-41.

JI Jing,XIAO Qiyan,HUANG Chao, et al. Research on deformation limits of performance-based RC shear walls controlled by flexure[J]．Journal of Building Structures，2010，31(9)：35-41.

[5] 清华大学、西南交通大学、北京交通大学土木工程结构专家组.汶川地震建筑震害分析[J].建筑结构学报,2008,29(4):1-9.

Civil and Structural Groups of Tsinghua University,Xinan Jiaotong University and Beijing Jiaotong University. Analysis on seismic damage of buildings in the wenchuan earthquake[J]. Journal of Building Structures, 2008,29(4):1-9.

[6] 梁岩.耐久性退化钢筋混凝土构件抗震性能及设计方法研究[D].长沙：中南大学，2014.

[7] 梁岩,罗小勇,张艳芳.反复荷载作用下锈蚀高强钢筋的性能变化[J].建筑材料学报,2015,18(1): 145-149.

LIANG Yan, LUO Xiaoyong, ZHANG Yanfang. Property changes of corroded high-strength steel bars under cycling load[J]. Journal of Building Materials, 2015, 18(1): 145-149.

[8] 梁岩，罗小勇,陈代海.锈蚀钢筋混凝土构件基于地震损伤的恢复力模型研究[J].振动与冲击,2015, 34(5):199-206.

LIANG Yan, LUO Xiaoyong,CHEN Daihai. Restoring force model of corroded reinforced concrete members undergoing seismic damage[J]. Journal of Vibration and Shock, 2015, 34(5): 199-206.

[9] 梁岩，陈淮，罗小勇.一般大气环境下钢筋混凝土构件抗震性能时随特征[J]．湖南大学学报，2016，43(3)：104-112.

LIANG Yan, CHEN Huai, LUO Xiaoyong. Time dependent seismic performance of reinforced concrete member under common atmosphere environment[J]．Journal of Hunan University，2016，43(3)：104-112.

[10] 梁岩，李杰，罗小勇.锈蚀钢筋混凝土构件抗震动力性能研究[J].振动工程学报,2016,29(1):140-147.

LIANG Yan, LI Jie,LUO Xiaoyong. Study on anti-seismic dynamic property of corroded reinforced concrete member[J].Journal of Vibration Engineering,2016,29(1): 140-147.

[11] 孙彬，牛荻涛，董振平.在役结构抗震评估地震作用取值研究[J]．西安建筑科技大学学报(自然科学版)，2003，35(4)：312-316.

SUN Bin, NIU Ditao, DONG Zhenping. Research on earthquake action for seismic assessment of existing structures[J]. J.Xi’an Univ. of Arch. & Tech. (Natural Science), 2003, 35(4): 312-316.

[12] 高小旺，鲍霭斌．地震作用慨率模型及统汁参数[J]．地震工程与工程振动，1985，5(1)：13-22.

GAO Xiaowang, BAO Aibin. Probabilistic model and its statistical for seismic load[J]．Earthquake Engineering and Engineering Vibration，1985，5(1)：13-22.

[13] 赵昕，董佩伟．高层建筑结构基于时变性能的抗震设计方法研究[J].地震工程与工程振动，2014，33(6)：115-121.

ZHAO Xin, DONG Peiwei. Tall building seismic design life-time time-dependent perfomance[J].Earthquake Engineering and Engineering Vibration，2014，33(6)：115-121.

[14] 刘恢先，广荣俭，陈达生．修订我国地震烈度表的一个建议方案[C]//地震工程研究报告集(第四集).北京：科学出版社，1981：1-13.

[15] PAULAY T，PRIESTLY M J N. Seismic design of reinforced concrete and masonry buildings[R]．New York：John Wiley，Inc., 1992.

[16] MANDER J B，PRIESTLY M J N，PARK R．Theoretical stress strain model for confined concrete[J].Journal of structural Engineering，ASCE，1998，114(8)：1804-1826．

[17] 周定松，吕西林，蒋欢军.钢筋混凝土框架梁的变形能力及基于性能的抗震设计方法[J].地震工程与工程振动，2005，25(4)：60-66.

ZHOU Dingsong,LÜ Xilin,JIANG Huanjun. Deformation capacity and performance-based seismic design method for RC frame beams[J]. Earthquake Engineering and Engineering Vibration，2005，25(4)：60-66.

[18] PRIESTLEY M J N. Brief comments on elastic flexibility of reinforced concrete frames and significance to seismic design[J].Bulletin of the New Zealand National Society for Earthquake Engineering，1998，31(4):245-259.

[19] 吕西林，周定松，蒋欢军.钢筋混凝土框架柱的变形能力及基于性能的抗震设计方法[J].地震工程与工程振动，2005，25(6)：53-61.

LÜ Xilin,ZHOU Dingsong, JIANG Huanjun. Deformation capacity and performance-based seismic design method for RC frame columns[J]. Earthquake Engineering and Engineering Vibration，2005，25(6)：53-61.

[20] 蔡立伦．含腐蚀钢筋之钢筋混凝土梁耐震行为[D]．台湾：国立台湾科技大学，2011.