基于噪声自检测的并行AdaBoost算法

徐 坚 陈优广

(华东师范大学 上海 200062)

0 引 言

数据分类问题作为数据挖掘领域中一个非常重要的研究方向，主要由两个阶段构成：学习和分类。学习阶段使用已知类别标记的数据集作为学习算法的输入，构筑分类器，而分类阶段则使用上一阶段得到的分类器预测未知标记数据的类别[1]。用于构筑分类器的方法有很多，如SVM、决策树和朴素贝叶斯模型等。在这些算法不断成熟完备的过程中，出现了诸如装袋(Bagging)、提升(Boosting)和随机森林等提高分类准确率的技术，这些被称为集成学习技术[2]。集成学习的原理为通过一定规则将一系列弱分类器集成提升为强分类器，再使用强分类器预测未知样本的类别标记。集成算法中，最具代表性的就是AdaBoost算法，该算法基于PAC框架提出,是集成算法中应用最为广泛的算法[3]。AdaBoost算法在诸如人脸识别，文本分类等诸多领域表现出众，算法通过反复迭代，可以将弱分类器的集合提升为强分类器,并且使训练误差以指数速度下降，训练集上的错误率趋近0[4]。但是AdaBoost算法同时也有一些缺点，Adaboost的每次迭代都依赖上一次迭代的结果，这就造成了算法需要严格按照顺序进行，随着迭代次数的升高，算法的时间成本也会相应的增大。基于这个缺点，Stefano Merler在2006年时提出了P-AdaBoost算法。利用AdaBoost在经过一定迭代次数的训练之后，并行地求出剩余弱分类器对应权重的训练误差，并证明了在经过足够次数的顺序迭代之后，并行AdaBoost的分类准确率跟传统AdaBoost相比基本相同甚至更高。然而他们没有考虑到数据集中存在的噪声会对结果造成负面的影响。AdaBoost本身是一个噪声敏感的算法，这是由于该算法在每次迭代时，都会将上次训练中分错的样本的权重加大，让本次训练的弱分类器更加关注这个被分错的样本。如果该错分样本是一个噪声，那么这个本来是噪声的样本的权重会在后续迭代过程中不断加大，导致后续弱分类器的分类准确率下降，最终导致整个模型的准确率随之下降[5]。

同时，在P-AdaBoost算法中，噪声比例的上升会导致算法构筑分类模型需要顺序迭代的次数变多，时间成本变高，得到的最终模型的分类准确度也会降低[6]。本文为了提高并行AdaBoost算法的分类准确率和健壮性，选择基于P-AdaBoost算法进行改进，在核心算法流程上保留了其构建模型时间较短的优势。同时通过修改权重分布的初始值，并利用噪声自检测方法减少数据集中的噪声对训练结果的影响，提出了一种名为ND-PAdaBoost (nosie-detection PAdaBoost)的算法，进一步提升算法训练结果的准确度。

1 AdaBoost算法概述

Adaboost的基本思想是通过不断迭代，利用已知类别标记的训练集训练出一系列弱分类器，然后将这些弱分类器线性结合在一起，得到一个分类准确率更高的强分类器。基分类器的训练算法种类很多，可以使用决策树、朴素贝叶斯等，还有学者提出也能使用神经网络作为算法的基分类器[7]。

AdaBoost算法流程如下：

输入：

1) 含有N个已知样本的训练集:

S={(x1,y1),(x2,y2),…,(xN,yN)}

(1)

2) 任意作为基分类器的分类算法。

输出：集成的最终模型G(x)。

步骤1初始化训练集每个样本的训练权重，均匀分布，每个样本赋值相同的权重。表示为：

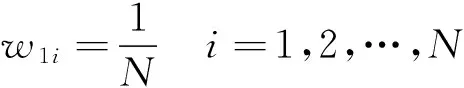
(2)

步骤2以T表示算法迭代的轮数，t表示是第t次迭代，Dt表示第t次迭代之后的样本权重分布，对于每一轮迭代有如下操作：

(1) 使用设置好权重Dt的训练集和选择的分类器算法进行训练，得到一个基分类器ht(x)∈{-1,+1}。

(2) 计算上一步中得到的分类器在训练集上分类的误差率，记为et：

(3)

其中：I(x)为指示函数，在x为真时取值为1，反之则为0。

(4) 利用得到的该分类器的误差率，计算该分类器对应的权重为：

(4)

该权重表示当前分类器在最终模型中的比重，也是最终模型中该分类器对应的系数。

(5) 更新训练数据集的样本权重，Dt+1=(wt+1,1,wt+1,2,…,wt+1,i,…,wt+1,N)，有：

(5)

(6)

其中：Zt作为归一化因子，用以确保每一轮的样本权重和为1。

步骤3将经过迭代后得到的一系列基分类器及其相应权重线性组合得到最终分类器，表示为：

(7)

2 P-AdaBoost算法概述

P-AdaBoost算法利用AdaBoost中权重分布的特性，通过一定次数的顺序迭代，用一种概率分布拟合样本权重的分布函数，使得后续训练得到的基分类器不用再通过上一次训练的结果更新计算本轮的权重，让后续的训练过程能够并行执行，优化了算法的时间成本，算法的建模效率得到明显提升。

2.1 权重动态分布

一权重的动态分布包含着许多关键的信息，这些信息在AdaBoost算法构建模型的时候起到了至关重要的作用[8]。AdaBoost训练基分类器时可以将样本简单地分为2类：易分类样本和难分类的样本。易分类样本在训练分类器的时候不容易被分错，根据AdaBoost算法原理，这些样本的权重会逐轮次降低，对新分类器训练起到的影响会越来越小。而难分类样本的权重并不会向一个固定值收敛，随着迭代次数的增加可能会发生随机波动。

一些研究人员的工作证明了难分类样本的权重分布遵从以下两个事实:(1) 对于任意一个难分类点，在基分类器数趋于无穷的情况下，该点的权重分布收敛于一个可确定的稳定分布；(2) 这一分布能够用参数选择适当的伽马分布来表示[9]，这使得算法能够并行计算出每轮迭代的样本权重。

2.2 P-AdaBoost算法流程

输入：

1) 含有N个已知样本的训练集S={(x1,y1),(x2,y2),…,(xN,yN)}；

2) 任意作为基分类器的分类算法。

输出：集成的最终模型G(x)。

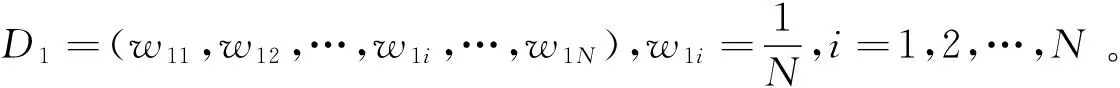
步骤2顺序迭代S轮的AdaBoost算法，保存每一轮的到的权重结果wi(s),s=1,2,…,S。

步骤4对S=S+1,S+2,…,T做如下操作(该循环能够并行执行)。

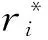
(3) 计算该模型对应的误差率es。

如果es<0.5，进行下一步。

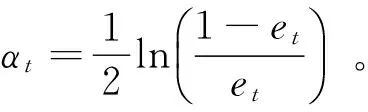
步骤5输出最终模型：

2.3 P-AdaBoost算法分析

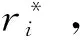
(8)

式中：α和θ的值是通过均值μ和方差σ2求解得到的，有如下关系：

μ=αθ

(9)

σ2=αθ2

(10)

3 ND-PAdaBoost算法概述

3.1 数据集不平衡问题

数据集中的数据分布不平衡问题在分类问题中经常出现，其主要表现为某一类的样本数远大于其他类别的样本数。而少数类又恰好是最需要学习的概念，由于少数类数据可能和某一特殊、重要的情形相关，造成了这类数据难以被识别。

诸如AdaBoost、P-AdaBoost等标准的学习算法考虑的是一个平衡数据集，当这些算法用到不平衡数据集时，可能会生成一个局部优化的分类模型，导致经常错分少数类样本[11]。因此AdaBoost和P-AdaBoost在平衡数据框架下分类准确率较高，然而在处理不平衡数据集时，分类准确率可能会下降。造成这种现象的主要原因如下：

(1) 分类准确率这种用以指导学习过程的，衡量全局性能的指标可能会偏向多数类，对少数类不利。

(2) 预测正例样本的分类规则可能非常的特殊，其覆盖率很低，训练过程中适应那些少数类的规则可能被丢弃。

(3) 规模非常小的少数类可能会被错误的当做噪声数据，同时真正的噪声会降低分类器对少数类的识别性能。

3.2 数据集中噪声样本的检测

真实世界中的数据集包含着各种各样的噪声。由于AdaBoost算法框架的特性，这些包含在数据集中的噪声会对算法生成的最终模型造成负面影响，导致过拟合的出现。造成这种结果的原因是AdaBoost算法在每次迭代之后会将之前分错的样本的权重提高，下一次迭代训练的分类器会着重针对这类权重高的样本学习，以此来最小化损失函数。然而由于大部分的噪声样本都不符合分类器的学习规则，导致噪声样本是很难被分类正确的。传统的AdaBoost没有对这种噪声样本进行处理，导致了这些样本随着迭代轮次的增长权重越来越大，后续训练的分类器偏向于这些权重大的噪声样本进行训练，使整个模型容易过拟合。而那些真正需要被正确分类的样本没有得到充分的学习，分类器的分类准确度下降，最终造成集成模型的分类准确度下降[12]。

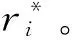
为了找出样本集中包含的噪声样本，本文考虑了这样的一种思路，因为每一个样本都是样本空间中的一个点。对于一个样本点(xi,yi)，已知一个分类模型ht(x)，如果该点在分类模型上取值yi与它邻近的点都不同，那么就有理由相信该点其实是一个噪声点。这是因为在分类的过程中，相同分类的点针对于一个已经训练出来的分类模型ht(x)的取值总是相近的。这标志了它们属于同一种分类并且这些点往往都集中分布在近邻的位置。如果这时有一个邻近点(其欧氏距离在一定范围内)的取值与其相邻的点在ht(x)上的取值都不同，这就说明了这个点即不能划归到另外一个分类。在欧氏距离上该点跟这些已分类点邻近，又不能将该点划为本分类，因为分类器的取值不同，所以该点就是一个噪声点。基于这一思想，本文提出了一种基于k邻近算法的噪声检测算法，并采用模拟随机噪声的方式进行验证，由于是随机噪声，所以无需在算法中针对噪声的分布做处理，算法流程如下：

输入：样本集S={(x1,y1),(x2,y2),…,(xN,yN)}，在S上训练得到的分类器ht(x)，k邻近算法的系数k。

输出：噪声样本集NS和非噪声样本集NNS。

步骤1对于每一个样本(xi,yi)循环进行如下操作：

计算(xi,yi)点可能为一个噪声点的概率为：

(11)

其中：I(x)为指示函数，在x为真时取值为1，反之则为0。

步骤2计算此概率在整个样本集上的平均为：

(12)

步骤3对于S上的每一个样本(xi,yi)做如下操作：

3.3 算法流程

考虑到迭代部分和并行部分对噪声处理的需求不同，本文在顺序迭代部分只将噪声的权重置为0，在进入并行流程之前用当前的分类器对数据集进行一次噪声监测，只保留非噪声样本为新的训练数据集。

详细的算法流程如下：

输入：

1) 含有N个已知样本的训练集S={(x1,y1),(x2,y2),…,(xN,yN)}，其中xi为样本矢量，yi∈{-1,+1}；

2) 任意作为基分类器的分类算法。

输出：集成的最终模型G(x)。

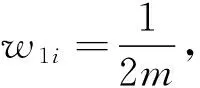
步骤2顺序迭代S轮的AdaBoost算法，在得到本轮训练生成的分类器ht(x)时，使用分类器对当前数据集运行噪声检测算法，将标记为噪声样本的权重设置为0，非噪声样本的权重按照传统算法进行更新。保存每一轮的到的权重结果wi(s)，s=1,2,…,S；

步骤3使用当前生成的集成分类器：

对数据集运行噪声检测算法,得到NS和NNS，使用NNS作为新的数据集S′；

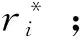
步骤5对S=S+1,S+2,…,T做如下操作(该循环能够并行执行)：

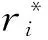
(3) 计算该模型对应的误差率es。

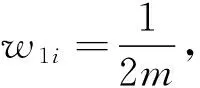
如果es<0.5，进行下一步；

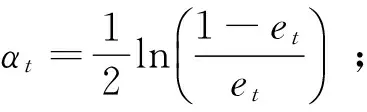
步骤6输出最终模型：

4 实 验

4.1 数据集

本文采用UCI(加州大学欧文分校)提供的机器学习公共数据集(见表1)，用以验证本文的算法相比于P-adaBoost、传统的AdaBoost和Bagging算法在相同数据集下分类结果的准确率更高。

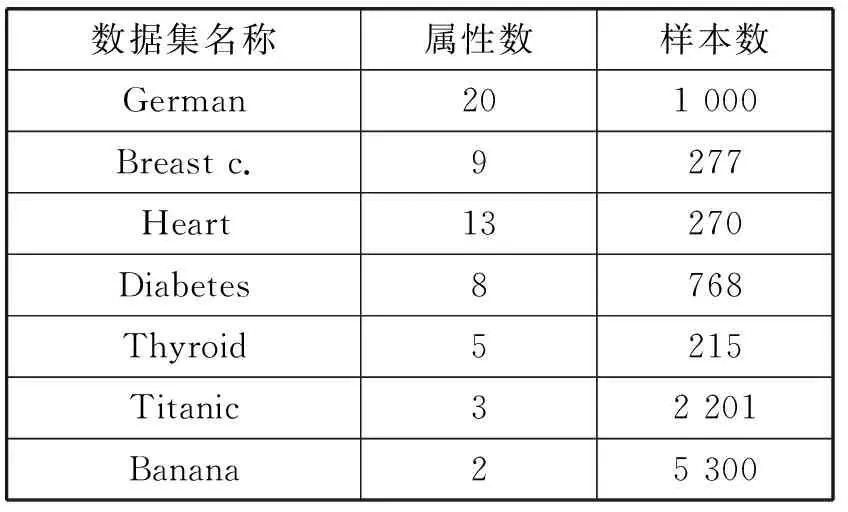
表1 数据集

4.2 实验方法

本文实验基于Weka平台，使用Java语言实现了ND-PAdaBoost算法。由于受实验条件所限,只模拟了ND-PAdaBoost算法并行运行的情况，由于模拟并不改变算法更新权重值的逻辑，所以其结果的分类准确率与算法真正并行运行的分类准确率一致，不影响对ND-PAdaBoost算法的评估和比较。实验对比了本文提出的ND-PAdaBoost算法和P-AdaBoost、传统AdaBoost、Bagging这四种算法在无噪声情况下的分类准确率。由于这四种算法流程上存在并行训练和连续迭代训练的区别，为了能充分验证本文提出算法ND-PAdaBoost的效果，该实验规定除Bagging算法外，其他含有连续迭代过程的算法的迭代轮次为100次。保证前三种算法的时间成本基本相同，并且本文通过反复实验证明了100次的顺序迭代足够使ND-PAdaBoost和P-AdaBoost算法估计出可信的样本权重分布。同时规定ND-PAdaBoost、P-AdaBoost和Baggaging这三种并行算法训练的总基分类器数目为500个，k邻近算法的系数设置为5%。实验记录各算法在无噪声下的分类准确率。

此外，为了说明本文改进权重初始值对算法分类准确率的提高产生了正面影响。本文在上述所有数据集上分别使用不同的初始值下的ND-PAdaBoost算法训练分类模型，NDP-AdaBoost的其余条件保持不变。通过比较最终分类模型的准确率来证明修改后的权重初始值有助于提高最终模型的分类准确率。

4.3 实验结果

实验结果如表2所示，其中加粗部分是每组数据集中正确率最高的，下划线部分是每组数据集中分类正确率最低的。通过该实验结果表明，ND-PAdaBoost算法即使在无噪声的数据集上的分类准确率相比于其他三种算法也有所提升。

表2 无噪声下各算法的分类准确率(100次迭代)

取Titanic、Diabetes数据集为例，比较前三种算法在不同噪声比例下的分类准确率。结果如表3所示。

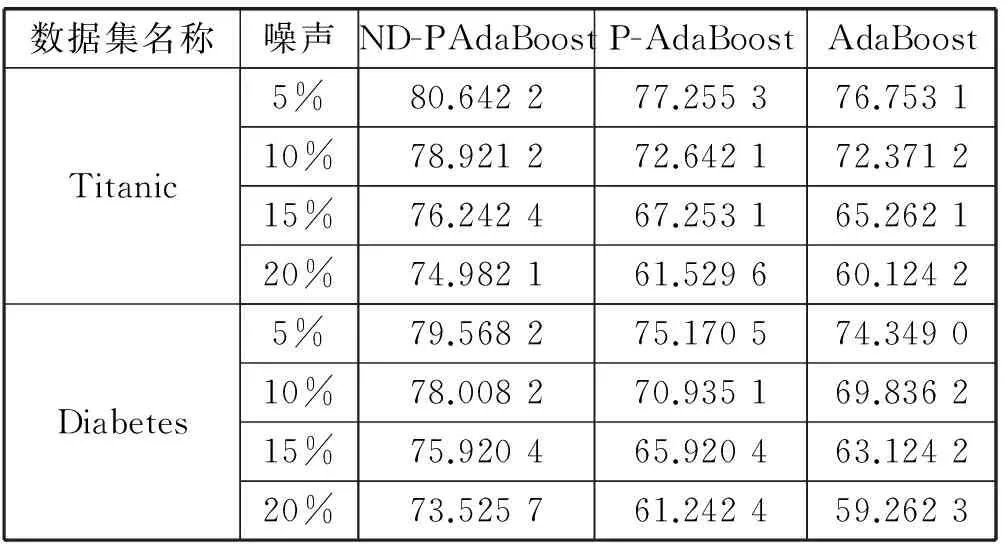
表3 不同噪声比例下各算法分类准确率

根据每组在不同噪声比例下的分类准确率绘制如图1和图2所示。

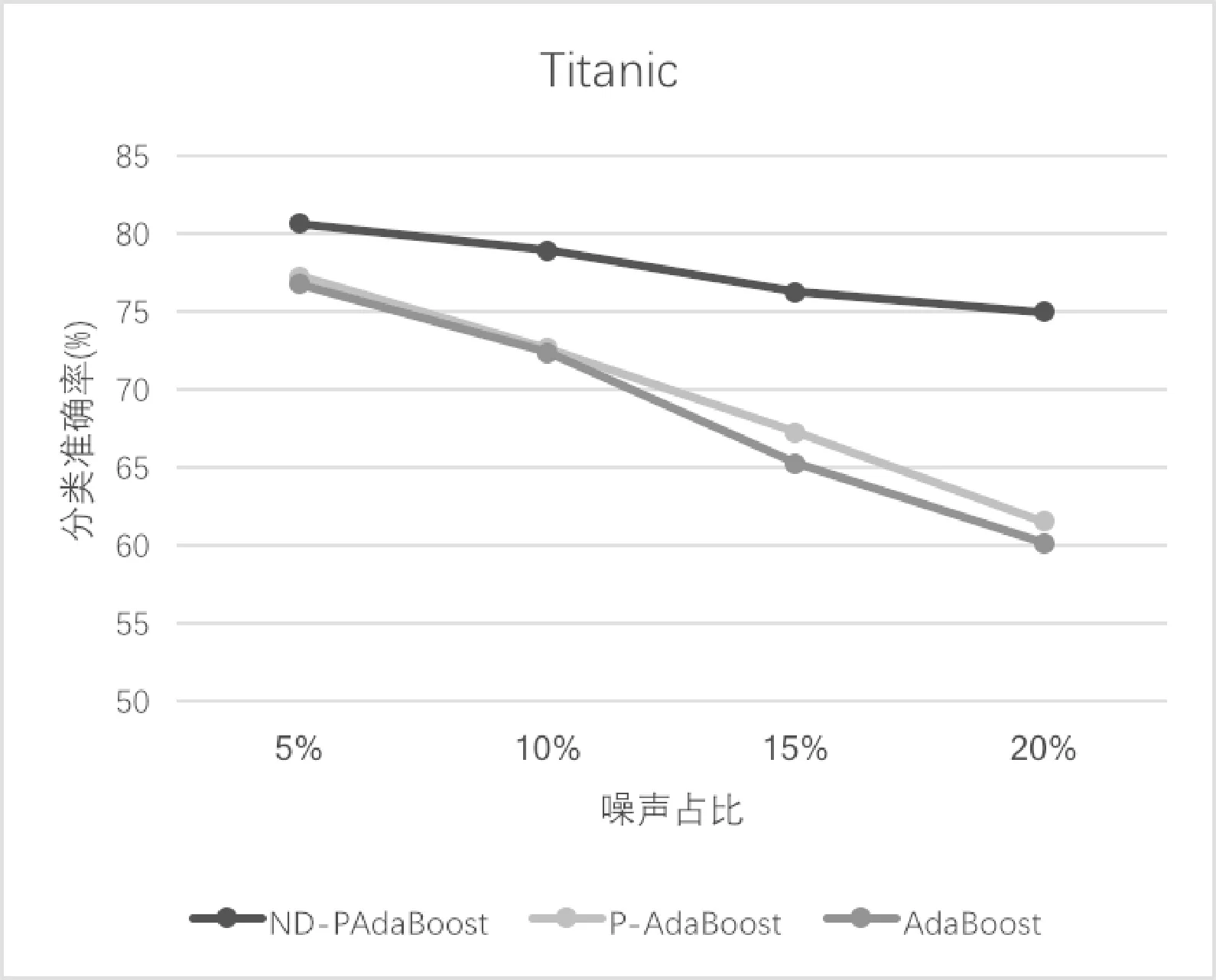
图1 Titanic数据集折线图

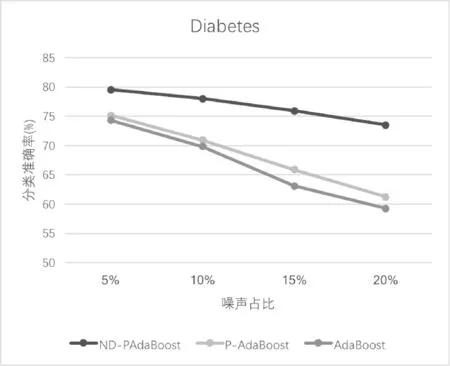
图2 Diabetes数据集折线图

由图1、图2可以看出，ND-PAdaBoost算法相比于P-AdaBoost和传统的AdaBoost对噪声有更好的兼容性，能够在含有噪声的数据集上取得更稳定的表现。随着噪声比例的增加，ND-PAdaBoost算法的分类准确率与P-AdaBoost和AdaBoost差距明显，一直维持在较高的水平。

表4 不同权重初始值下ND-PAdaBoost算法分类准确率

5 结 语

本文从AdaBoost算法的框架出发，基于AdaBoost的并行改进算法P-AdaBoost,针对P-AdaBoost对噪声敏感，含有噪声的数据集会严重影响P-AdaBoost分类准确度的问题，提出了一个噪声自检测方法,并修改了原始样本权重分布的初始值。本文使用了UCI数据集对提出的改进方法进行了多番验证。实验结果表明，本文提出的算法在输入数据集含噪声的场景下具有更好的分类准确率。然而，本文提出的模型只准对二分类问题有效，如果需要推广到多分类问题上，还需要对模型进行修改。本算法中所需顺序迭代次数的取值是通过反复实验测定的，关于这个取值的最优数值还需要进一步的研究和探讨。

[1] 周志华.机器学习[M].北京:清华大学出版社,2016:121-145.

[2] Breiman L.Bagging predictors[J].Machine Learning,1996,24(2):123-140.

[3] Breiman L.Random Forests[J].Machine Learning,1996,24(2):123-140.

[4] Nie Q,Jin L,Fei S.Probability estimation for multi-class classification using AdaBoost[J].Pattern Recognition,2014,47(12):3931-3940.

[5] 曹莹,苗启广,刘家辰,等.AdaBoost算法研究进展与展望[J].自动化学报,2013,39(6):745-758.

[6] Merler S,Caprile B,Furlanello C.Parallelizing AdaBoost by weights dynamics[J].Computational Statistics & Data Analysis,2007,51(5):2487-2498.

[7] 李翔,朱全银.Adaboost算法改进BP神经网络预测研究[J].计算机工程与科学,2013,35(8):96-102.

[8] Caprile B,Furlanello C,Merler S.Highlighting Hard Patterns via AdaBoost Weights Evolution[J].Lecture Notes in Computer Science,2002,2364:72-80.

[9] Collins M.Logistic regression,Adaboost and bregman distances[J].Machine Learning,2002,48(1):253-285.

[10] Htike K K.Efficient determination of the number of weak learners in AdaBoost[J].Journal of Experimental & Theoretical Artificial Intelligence,2016,29(5):1-16.

[11] Lee W,Jun C,Lee J.Instance categorization by support vector machines to adjust weights in AdaBoost for imbalanced data classification[J].Information Sciences,2017,381:92-103.

[12] Barrow D K,Crone S F.A comparison of AdaBoost algorithms for time series forecast combination[J].International Journal of Forecasting,2016,32(4):1103-1119.