仔细探索规律，准确确定范围

吉沙娟

在圆锥曲线中，很多同学在求点的轨迹方程时常常把握不住范围，其实范围的确定是有一定的规律可循的，下面通过例题来揭示这些规律.

一、定义中的限制条件带来的范围

例1已知一个动圆M与两定圆C1：（x＋4）2＋y2＝1，C2：（x-4）2＋y2＝9均外切，求动圆圆心M的轨迹方程.

解析设动圆圆心M（x，y），动圆的半径为r，则根据题意得

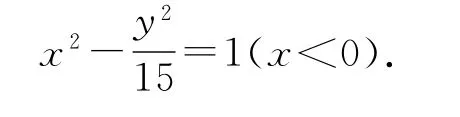
反思小结由于双曲线的定义中有“差的绝对值”这个限制条件，所以如果仅是“差”，那么动点的轨迹往往是双曲线的一支.据此可知，定义中的限制条件带来了轨迹方程中的限制范围.

总结所有圆锥曲线的定义的限制条件如下：

1.双曲线的定义中有两个限制条件，一个是“差的绝对值”，一个是“差必须小于两个定点的距离”；

2.椭圆的定义中有一个限制条件，就是“和必须大于两个定点的距离”；

3.抛物线的定义中有一个与椭圆、双曲线都不一样的限制条件是“定点不在定直线上”；

4.圆锥曲线的统一定义是“平面内到一个定点F和到一条定直线l（F不在l上）的距离的比等于常数e的点的轨迹”，其中也有一个限制条件，就是“F不在l上”，不仅如此，还需要关注点F是在l的左方还是右方，或者是上方还是下方，以便确定范围.

二、题设中的限制条件带来的范围

例2已知一个等腰三角形的顶点A（3，20），一个底角顶点为B（3，5），求另一个底角顶点C的轨迹.

解析设点C（x，y），根据题意有AB＝AC，则15，即（x-3）2＋（y-20）2＝225.

考虑到三角形的三个顶点是不共线的，所以x≠3，故所求顶点C的轨迹就是以顶点A（3，20）为圆心、15为半径的圆（除去点B（3，5）和点（3，35））.

例3动圆C：（x-1）2＋y2＝1，过原点O作圆的任意一条弦，求弦的中点的轨迹方程.

解法1（直接法）设OQ为过O的任一条弦，P（x，y）是其中点，由题知CP⊥OQ，即所以 （x-1，y）·（x，y）＝0，即.考虑到弦的中点在动圆C内，所以x≠0，即所求的轨迹方程为

解法2（定义法）因为∠OPC＝90°，动点P在以圆心，OC为直径的圆上，所以所求点的轨迹方程为

解法3（参数法）设动弦OQ的方程为y＝kx，由得：（1＋k2）x2-2x＝0.

设O（0，0），Q（x2，y2），OQ的中点为P（x1，y1），则：

反思小结题设中的限制条件有时是显性的，有时是隐性的.比如条件中“三角形”“弦的中点”分别是显性和隐性的，不管是哪类都需要转化才能获得正确的范围，如果多运用数形结合的思想将有利于转化.

三、推理运算过程中带来的范围

例4已知动点P（x，y）的坐标满足（为参数），求动点 的坐标 ，tPxy满足的普通方程.

解析将两边平方，与y＝联立消去t，不难得到y＝x2-2，而x＝可知x≥2或x≤-2，所以动点P满足的普通方程是y＝x2-2（x≥2，或x≤-2）.

反思小结利用参数法是求动点的轨迹方程的一种方法，在消去参数的过程中要注意推理的等价性.

确定轨迹的范围是处理轨迹问题的难点，也是我们最容易出现错误的地方，所以在平时的学习和练习中，既要对基本的概念和公式理解透彻，也要准确理解题意，挖掘隐含条件.另外，这部分研究的对象是平面几何，所以图形是其本质，坐标法是解决问题的方法，在分析题意时多画图，也便于看清题目的本质.