例谈类比思维的运用

张圣官

类比推理就是根据两个对象或两类事物间存在着的一系列相同或相似的属性，猜测它们之间也可能具有的其他一些相同或相似的属性的思维方法.波利亚说过：“类比是某种类型的相似性，是一种更确定的和更概念性的相似.”类比推理的思维过程大致是：观察、比较→联想、类比→猜测新的结论.类比是提出新问题和作出新发现的一个重要源泉，是一种较高层次的信息迁移.下面以高考试题为例给予分类剖析，希望能对大家有所启迪.

一、特殊向一般类比

由特殊向一般类比，提升同学们的发散思维、理性思维，也即是通常所讲的“推广”.

例1已知函数有如下性质：如果常数a＞0，那么该函数在上是减函数，在上是增函数.试研究函数（常数c＞0）在定义域内的单调性，并说明理由.

解（1）设

当n是奇数时，函数在上是减函数，在上是增函数，在上是增函数，在上是减函数；

当n是偶数时，函数在上是减函数，在上是增函数，在上是减函数，在上是增函数.

点评一般函数是特殊函数在形式上的推广，两者结构形式类似，可以进行类比.事实上，令u＝xn，则y＝即化为形如的函数，结论也更容易获得.

二、抽象向具体类比

将抽象问题向具体问题类比，锻炼我们思维的灵活性和化归能力.

例2已知f（x）是定义在R上的不恒为0的函数，且对于任意的a，b∈R都满足：f（ab）＝af（b）＋bf（a）.

（1）求f（0），f（1）的值；

（2）判断f（x）的奇偶性，并证明你的结论；

（3）若f（2）＝2，N*），求数列｛Un｝的前n项和Sn.

解（1）f（0）＝0，f（1）＝0；（2）f（x）是奇函数，证明略；（3）当ab≠0时令则g（ab）＝g（a）＋g（b）.

类比对数函数的性质，易得g（an）＝ng（a）.

所以f（an）＝ang（an）＝nang（a）＝nan-1f（a）.

因为f（2）＝2，所以

点评以上将抽象函数g（x）类比到对数函数，发现了相关结论，从而打开了解题思路.

三、低维向高维类比

由低维向高维类比，属于开放性题型，对于提高我们的探究能力和想象力大有帮助.

例3如图1，点P为斜三棱柱ABCA1B1C1的侧棱BB1上一点，PM⊥BB1交AA1于点M，PN⊥BB1交CC1于点N.

（1）求证：CC1⊥MN；

（2） 在 任意△DEF中有余弦定理：DE2＝DF2＋EF2-2DF·EFcos∠DFE，拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并予以证明.

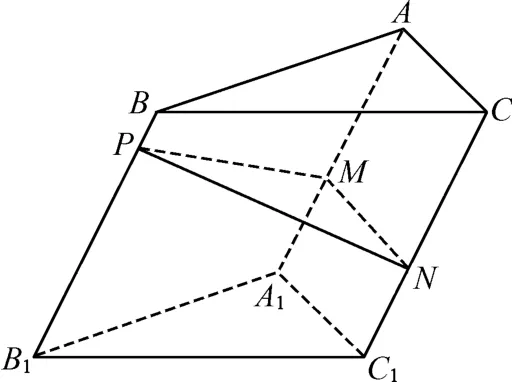
图1

解（1）因为CC1∥BB1⇒CC1⊥PM，CC1⊥PN，所以CC1⊥平面PMN⇒CC1⊥MN；

因为CC1⊥平面PMN，所以上述的二面角为∠MNP.

在△PMN中，

四、平行性类比

这是在两类相近事物的性质间进行的类比，如等差数列与等比数列，椭圆和双曲线等.

例4已知椭圆具有性质：若M，N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM，PN的斜率都存在，并记为kPM，kPN时，那么kPM·kPN是与点P位置无关的定值.试对双曲线（a＞b＞0）写出具有类似特性的性质，并加以证明.

解若M，N是双曲线（a＞b＞0）上关于原点对称的两个点，点P是双曲线上任意一点，当直线PM，PN的斜率都存在，并记为kPM，kPN时，那么kPM·kPN是与点P位置无关的定值.

证明如下：设M（x1，y1），则N（-x1，-y1），又设P（x，y），

五、方法性类比

这是将某一数学内容的处理方法迁移到另一数学对象中的一种手段，如课本上的方法类比到课外习题中，是较高层次上的类比.

例5设，利用课本推导等差数列前n项和公式的方法，可求得f（-5）＋f（-4）＋…＋f（0）＋…＋f（6）的值为________.

解析类比等差数列求和的倒序相加法，由，可得：

设S＝f（-5）＋f（-4）＋…＋f（0）＋…＋f（6），

则S＝f（6）＋f（5）＋…＋f（0）＋…＋f（-5），

所以2S＝[f（-5）＋f（6）]＋[f（-4）＋f（5）]＋…＋[f（6）＋f（-5）]＝

所以f（-5）＋f（-4）＋…＋f（0）＋…＋f（6）的值为

点评课本是知识之本、方法之根，课本上的题目、概念、方法看似简单，但却是最基本、最重要的，从课本出发，加以类比、推广、拓展，可以进而解决复杂问题，切不可轻视课本啊！

巩固练习

1. 已知两个圆：x2＋y2＝1 ①与x2＋（y-3）2＝1 ②，则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广，即要求得到一个更一般的命题，而已知命题应成为所推广命题的一个特例.推广的命题为____________________.

2. 在等差数列｛an｝中，若a10＝0，则有等式a1＋a2＋…＋an＝a1＋a2＋…＋a19-n（n＜19，n∈N*）成立.类比上述性质，相应地：在等比数列｛bn｝中，若b9＝1，则有等式_________________成立.

参考答案

1.本题是由圆（特殊的）到圆（一般的）之间的类比，也就是数学研究中的一般化方法，即从特例中抽象出共同的特性.本题的关键之处是两圆半径必须相等，即由圆方程（x-a）2＋（y-b）2＝r2①与（x-c）2＋（y-d）2＝r2②（a≠c或b≠d）相减，可得它们的对称轴方程为2（c-a）x＋2（d-b）y＋a2＋b2-c2-d2＝0.

2.这是由一类事物（等差数列）到与其相似的一类事物（等比数列）间的类比.在等差数列｛an｝前19项中，其中间一项a10＝0，则a1＋a19＝a2＋a18＝…＝an＋a20-n＝an＋1＋a19-n＝2a10＝0，所以a1＋a2＋…＋an＋…＋a19＝0，即a1＋a2＋…＋an＝-a19-a18-…-an＋1.又因为a1＝-a19，a2＝-a18，…，a19-n＝-an＋1，所以a1＋a2＋…＋an＝-a19-a18-…-an＋1＝a1＋a2＋…＋a19-n.相似地，在等比数列｛bn｝的前17项中，b9＝1为其中间项，则可得结论b1b2…bn＝b1b2…b17-n（n＜17，n∈N*）成立.