基于有限元分析的潜艇直流输电线路电感计算
2018-02-26王琦袁建生赵启明
王琦,袁建生,赵启明
1武汉科技大学信息科学与工程学院,湖北武汉430081
2清华大学电机工程与应用电子技术系,北京100084
0 引 言
潜艇直流输电网络具有电压低、线路短、网络结构简单的特点,其电压等级通常不高于直流电1 000 V,输电电缆长度通常不超过1 km,为干馈式电网结构。在正常运行工况下,输电线路的计算参数以电阻为主,但在对电网进行短路故障分析计算时,输电线路电磁特性对短路电流影响较大,此时线路电感值不能忽略。目前,针对潜艇直流电网的电源和负载的研究较多[1-3],对线路电缆的研究主要集中在交、直流混合供电时的电磁干扰情况下[4-5],而针对输电电缆电感参数的计算较少。在潜艇直流电网设计中,通常根据厂家给定电缆册中的电缆参数进行电感计算。然而,直流输电线路实际电感参数值受线路形成的回路、电缆敷设环境、电缆间距等环境的影响。在不同的环境中,线路实际电感值与传统方法得到的计算值差别较大。输电线路电感值会影响系统暂态特性计算,进而影响相应的设计指标。针对陆地电网中的多端直流输电电网,近年来公开发表了多篇文章,主要分析其输电线路模型和参数计算方法。董艺等[6]研究了不同回流方式、回流线和金属护套下的电缆正序,特别是零序的阻抗的计算方法,提高了高压电缆参数计算的准确性;Akkari等[7]讨论了采用不同直流电缆等效电路模型对陆地高压直流电网进行特性分析时所产生的不同影响;杜学龙等[8]提出了一种考虑大地影响的高速铁路轨道电路互阻抗快速计算方法,获得了较好的计算效果。与上述研究中的电网对象相比,潜艇直流电网中的直流电压等级较低,电缆流过的直流电流大,且电缆在潜艇有限空间内排列更加紧密,因此需要分析现有方法在计算潜艇直流电网输电线路电感参数时的适用性。
本文将首先阐述潜艇直流输电电缆敷设特点,分析常用的线路电感计算式在潜艇直流输电线路电感计算中的适用性,并在ANSYS/Maxwell软件中搭建某潜艇直流电网短路试验系统的输电线路模型,采用有限元分析(Finite Element Analysis,FEA)法计算输电线路总电感值。然后利用Matlab/Simulink软件仿真试验系统,将仿真得到的短路电流波形和实验实测短路电流波形相比较,分析不同的输电线路电感计算方式得到的等效电感数值对系统短路电流波形的影响。
1 潜艇直流输电线路敷设状态
潜艇由于空间狭小,通常将多根输电电缆紧凑排列后进行敷设,并设计电缆导板,固定电缆位置。电缆穿舱导板如图1所示(材料相对磁导率接近于1),电缆间距相对于电缆导体半径很小,输电线路电感计算需要充分考虑电缆本身的结构、敷设以及电缆使用方式。
2 潜艇直流输电线路电感分析
2.1 回路等效电感
由文献[9]可知,一个回路如果通以电流I,由此电流所建立的与该回路交链的磁链ψ与电流I的比值称为该回路的自感系数,简称自感,用L表示,即
从式(1)可知,一个回路构成电感,I为通入回路的电流,ψ为回路围成的面积上的磁链。
对电力系统进行分析计算时,通常需要建立系统等效电路模型。在电路[10]中,电感元件是1组线圈,反映了电流产生磁通和磁场能量储存这一物理现象,其元件特性是磁通链ψ与电流I的代数关系:
在这里,容易将回路等效电感和电感元件混淆。对电感元件而言,其电感值是确定值。而回路等效电感则由所在回路确定。在电缆设计手册中,电缆厂家通常会给出50 Hz的电缆电感值,但由于该电感值的测试环境与潜艇输电电缆实际敷设环境相差甚远,即构成的回路不相同,而且回路总电感受电缆之间距离和电缆半径等综合环境的影响,所以采用电缆铭牌值中的单位长度电感值进行短路电流计算时易导致较大误差。
2.2 常用电感计算公式适用性分析
2.2.1 内自感和外自感的计算
根据电感的定义,其计算式如下[9]:
式中:Li为内自感,等于与导线的部分电流交链的磁链与导线电流之比;Le为外自感,等于与导线的全部电流交链的磁链与导线电流之比。利用毕奥—赛伐尔定律对其形成的磁场中的磁链进行积分,可分别得到其内自感和外自感计算公式:
式中:μ0=4π×10-7H/m ,为真空磁导率;r1为芯线半径;r2为外层导体圆半径;l为电缆长度。
通过分别求回路内自感、外自感来获得回路总电感值的传统计算方法,只有在能够区分内、外磁链区域,即内、外磁链无重叠时,才能精确计算总电感。采用传统方法计算长直平行双导线电感时,线间距离和导线半径的比值越小,计算误差越大。
2.2.2 单根圆柱形长导线单位自感的计算
在电力系统分析[11]中,通常采用的单根圆柱形长导线的电感计算公式为
2.3 实艇输电线路电感值分析
在潜艇中常用到2种电力电缆:一种不带屏蔽层;一种带屏蔽层。结构分别如图2和图3所示。电缆的使用方式也不同,对于不带屏蔽层的电缆,需要一根电缆导体连接电源正极,另一根电缆导体连接电源负极形成回路。对于带屏蔽层的电缆,可以由自身的导体与屏蔽层形成回路(图4),也可以通过两根电缆的导体形成回路(图5)。
当电缆的使用方式如图4所示时,导体和屏蔽层分别连接电源正、负极,回路所围面积全部在电缆内部,产生的磁场集中在电缆内,电缆外磁场为0。当多根屏蔽电缆采用这种回路接线方式并联输电时,每根电缆所产生的磁场互不影响。设一条输电线路的电缆阻抗为X1,当输电线路电缆根数从1增加到n时,线路等效阻抗为Xn,各条电缆之间无电磁串扰,存在线性关系
当电缆的使用方式如图5所示时,屏蔽电缆没有自成回路,正极线路和负极线路之间磁场所覆盖的面积不仅仅在电缆线内部,还包括电缆外的空间。多条回路产生的磁场会相互耦合,由多根电缆并联形成的输电线路总电感与单根电缆电感不存在线性关系,即在低频磁场分析中,由于屏蔽电缆中电流只在导线中流过,此时的屏蔽电缆回路电感计算与普通电缆、裸露导体无异。
3 基于有限元分析的电感计算
3.1 计算原理
有限元分析理论是采用有限数量的未知量去逼近无限未知量的真实系统,将复杂问题用简单的问题代替并求解。目前,有限元分析已经被大量运用到对场域的分析计算中,并取得了较好的效果。ANSYS/Maxwell是目前应用十分广泛的低频电磁场有限元软件之一,在工程电磁领域得到了广泛的应用[12-13]。在参数计算中,ANSYS/Maxwell软件利用磁场能量来计算。磁场能量与电感和电流的关系为
式中:Wm为磁场能量;L总为回路总电感;I总为回路总电流。
根据软件计算出的回路能量值,可得回路总电感为
能量是通过磁场在整个场域中的积分得到的,即
式中,H为磁场强度;B为磁感应强度;V为电缆的阻抗。
3.2 模型建立
实验系统采用艇用某型电池和直流电力电缆(JYJPJ85SC-1)。根据实艇电缆敷设情况,设计电缆导板,固定试验系统中的电缆位置。直接用开关连接正、负极电缆末端,控制开关的闭合来模拟系统发生短路故障。实验系统如图6所示。
在ANSYS/Maxwell软件中建立电缆模型,流程图如图9所示。
图10为电缆模型图,其中图10(a)为模型整体图,图10(b)为有限元网格局部放大图。图11显示了采用有限元分析计算所得出的输电线路磁场分布情况。从中可以看出,每条回路所产生的磁场耦合严重,而且磁路形态较为复杂,磁场总能量集中在回路所围的面积内。
3.3 电感计算结果与测量结果的对比分析
针对实验系统的输电线路,分别通过有限元法计算和实体测量,得到如表1所示的回路总电感数据。图12为回路总电感随频率变换的特性曲线,反映出回路总电感随着激励(电流)频率的升高而逐渐减小,最后趋于稳定。
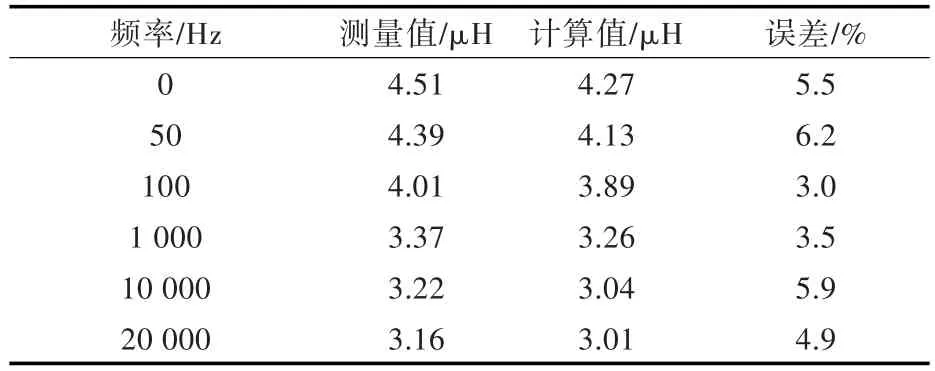
表1 回路总电感Table 1 Inductance values
如果忽略电缆之间的耦合关系,通过电缆铭牌值得到50 Hz时,回路总电感值为1.48 μH。从表1和图12中可知,采用有限元计算和实际测量所得出的回路总电感比采用电缆给定铭牌值计算得到的总电感要大,接近其3倍,说明实艇敷设状态使得各条并行回路之间耦合严重。
4 线路电感计算值对潜艇直流系统短路电流的影响分析
在实验过程中,经霍尔探头测量得到短路电流信号波形,在示波器中显示曲线如图13所示。将示波器中的数据导出后,得到图14中曲线①所示波形。
在Matlab/Simulink软件中,对实验系统的短路故障状态进行建模仿真,其中,蓄电池组通过电源串联自电阻和自电感来模拟。线路建模直接采用电阻串联电感的形式。将得到的短路电流仿真波形和实验实测波形相比较,得到了如图14所示的短路电流波形对比图。图14中:曲线①为实验系统实测短路电流波形;曲线②为输电线路用有限元分析计算总阻抗时得到的短路电流波形;曲线③为输电线路用电缆铭牌值参数得到的短路电流波形;曲线④为直流输电线路忽略电感采用纯电阻模拟时得到的短路电流波形。
从图14中可以看出,4条短路电流曲线均有一个暂态过程,最后达到稳态值。实际系统的短路电流波形时间常数为12.6 ms,经过0.5 s达到最大值。当T=10ms时,I1=5 489 A,I2=6 532 A,I3=7 988 A,I4=8 900 A。在直流系统暂态计算中,如果完全忽略线路电感的影响,则开关瞬时动作能力需要在10 ms时具备切断8 900 A电流的能力。而在实际系统中,此时的短路电流才达到5 489 A。采用不恰当的电感值会造成短路电流计算值过大,从而加大保护系统的设计难度。另从图14中也可知,采用有限元方法计算得到的电感值更加接近于实际系统,提高了计算精度。
5 结 论
本文通过搭建实艇短路试验系统模拟了潜艇直流电网短路故障,测量了实验电缆参数,建立了实验系统输电线路计算仿真模型,并采用有限元法进行了线路电感计算,对比分析了实验波形和仿真波形,主要研究结论如下:
1)由于潜艇直流主电网布置空间紧凑,各条输电回路存在强耦合,陆地电网中利用大地形成回路以及忽略电线间电磁影响的输电线路等效电感计算方法已不适用。
2)根据实艇电缆敷设情况建立模型,并采用有限元分析计算线路等效总电感值的方法,能够有效提高对潜艇直流输电线路等效总电感值计算的精度,更好地适应潜艇直流电网的暂态计算需求,从而减小直流电网暂态分析中的误差。
[1]AURILIO G,GALLO D,LANDI C,et al.A battery equivalent-circuit model and an advanced technique for parameter estimation[C]//2015 IEEE International Instrumentation and Measurement Technology Conference(I2MTC).Pisa:IEEE,2015:1705-1710.
[2]李大鹏,张晓东.俄罗斯非核动力潜艇推进系统的选择与发展趋势[J].中国舰船研究,2011,6(6):102-108.LI D P,ZHANG X D.Solutions and development trends of Russian navy's non-nuclear submarine propulsion system[J].Chinese Journal of Ship Research,2011,6(6):102-108(in Chinese).
[3]厉行军,赵建华,杨建冰,等.现代潜艇铅酸蓄电池充电模型[J].舰船科学技术,2011,33(4):58-61.LI X J,ZHAO J H,YANG J B,et al.Research on the charge model of lead-acid batteries onboard modern submarines[J].Ship Science and Technology,2011,33(4):58-61(in Chinese).
[4]范昕.舰船电力系统电磁兼容性研究现状综述[J].中国舰船研究,2013,8(3):78-84.FAN X.A review of the research status on the EMC of ship power systems[J].Chinese Journal of Ship Research,2013,8(3):78-84(in Chinese).
[5]李杰,单潮龙.DC电缆模型对电磁干扰仿真的影响[J].船电技术,2010,30(4):14-19.LI J,SHAN C L.DC cable model affection to simulation of EMI[J].Marine Electric&Electronic Technology,2010,30(4):14-19(in Chinese).
[6]董艺,胡铁军,张灿淋,等.高压电缆线路序阻抗参数的精确计算研究[J].电力科学与工程,2013,29(10):6-12.DONG Y,HU T J,ZHANG C L,et al.The accurate calculation of high voltage cable line's sequence impedance[J].Electric Power Science and Engineering,2013,29(10):6-12(in Chinese).
[7]AKKARI S,PRIETO-ARAUJOY E,DAI J,et al.Impact of the DC cable models on the SVD analysis of a multi-terminalHVDC system [C]//Proceedingsof 2016 Power Systems Computation Conference(PSCC).Hong Kong,China:IEEE,2016:1-6.
[8]杜学龙,王智新,邹军.考虑大地影响高速铁路轨道电路互阻抗快速计算简化公式[J].电工技术学报,2016,31(4):1-6.DU X L,WANG Z X,ZOU J.A fast and simplified formula for calculating the mutual impedance with the earth return of the high-speed railway track circuit[J].Transactions of China Electrotechnical Society,2016,31(4):1-6(in Chinese).
[9]马信山,张济世,王平.电磁场基础[M].北京:清华大学出版社,1995:128-142.
[10]邱关源.电路[M].4版.北京:高等教育出版社,1999:12-14.
[11]何仰赞.电力系统分析(上)[M].4版.武汉:华中科技大学出版社,2016:10-18.
[12]辛瑞昊,熊庆辉,王浚哲,等.基于Maxwell的电磁阀仿真与分析[J].长春理工大学学报(自然科学版),2015,38(2):113-116.XIN R H,XIONG Q H,WANG J Z,et al.Simulation and analysis of soleniod valves based on Maxwell[J].Journal of Changchun University of Science and Technology(Natural Science Edition),2015,38(2):113-116(in Chinese).
[13]何淼,CHEN G,LEWIN P L.内部缺陷对高压直流电缆电场分布影响的有限元分析[J].南方电网技术,2015,9(10):83-91.HE M,CHEN G,LEWIN P L.Analysis on influence of internal defect on electric field distortion of HVDC cable with finite element method[J].Southern Power System Technology,2015,9(10):83-91(in Chinese).
