纵横加筋圆锥壳振动特性多目标优化设计

刘东，王春旭，刘均，张攀，程远胜

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2中国舰船研究设计中心，湖北武汉430064

0 引 言

加筋圆锥壳是水下结构物轴系系统的支撑结构，其振动特性对于结构整体的振动以及声学性能有着重要影响。如何降低加筋圆锥壳结构在轴系转动激励下的结构响应，成为水下结构物声学设计需要解决的关键问题。为了优化外部激励下加筋圆锥壳的结构响应，国内外学者开展了许多研究。Liu等［1］提出了一种浸水变厚度圆锥壳在低频下的自由振动分析方法。Liu等［2］采用Flügge经典薄壳理论和环形加筋等效法，导出了流体载荷下环肋阶梯锥壳的运动微分方程。Wang等［3］提出了一种精确的传递矩阵，用来计算圆锥壳的结构及声学响应。周云泽等［4］采用幂级数法计算了圆锥壳固有频率的收敛性和准确性。陈美霞等［5］采用波动法建立了带框架肋骨加筋圆柱壳数学模型，并对其自由振动特性和频响特性进行了研究。瞿叶高等［6］提出了一种分区广义变分和最小二乘加权残值区域分解法，用来分析圆锥壳—圆柱壳—圆锥壳组合结构的自由振动。肖伟等［7］以容积重量比为目标，采用多目标分层序列优化法和遗传算法对纵横加筋圆柱壳进行了优化分析。李学斌等［8］针对环肋圆柱壳在静水压力作用下的多目标离散优化问题进行了研究，并给出了不同目标之间的Pareto前沿。叶文荣等［9］应用有限元软件对单层圆柱壳进行了基于离散变量的动态性能优化设计。但目前针对圆锥壳的声学特性多目标优化的研究还较少。

本文将以纵横加筋圆锥壳为研究对象，以壳板厚度和纵横筋尺寸为设计变量，以结构第1阶总体弯曲模态频率和低频范围加筋圆锥壳尾端载荷处加速度总级为优化目标，考虑结构重量约束条件，建立其多目标优化数学模型，并采用宽容排序法与遗传算法进行求解。最后，研究重量约束与宽容度对优化结果的影响。

1 加筋圆锥壳有限元模型

1.1 结构参数化表征

根据结构的特点，选取如表1所示的参数作为有限元参数化建模的基本参数。变厚度圆锥壳如图1所示。

1.2 有限元模型及结构分析

加筋圆锥壳有限元模型通过有限元软件ANSYS建立，壳体及壳体以上的纵筋和环筋的腹板均采用壳单元（Shell 181）模拟，纵筋和环筋的面板均采用梁单元（Beam 188）模拟。

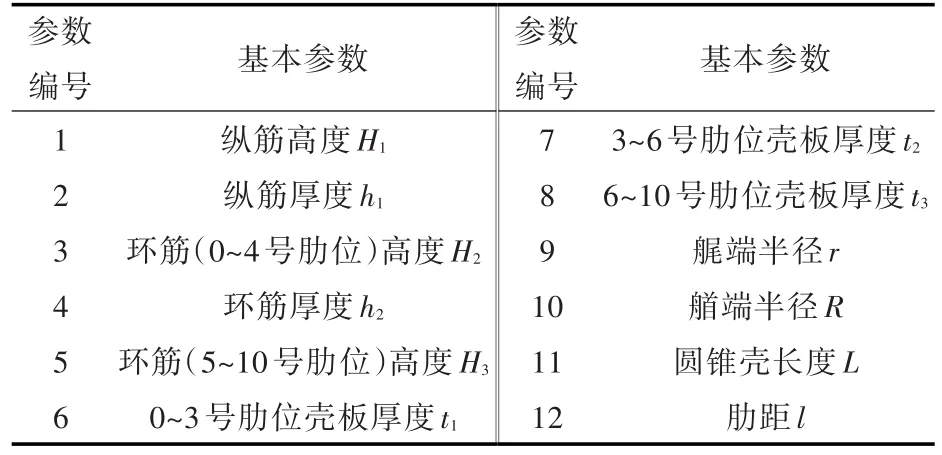
表1 基本参数Table 1 Basic parameters

壳体与纵筋、环筋均为钢质，材料密度为7 850 kg/m3，杨氏模量为 210 GPa，泊松比为 0.3。

边界条件为在艏端壳体上施加简支约束，激励为在壳体艉端中纵剖面上施加垂直向下的单位力，如图2所示。

网格收敛性计算分析表明，在纵筋和环筋腹板高度方向上划分3个单元，沿环向0～4号肋位在壳体上划分72个单元，沿5～10号肋位在壳体上划分48个单元，其余部分结构均采用200 mm的网格尺寸计算，结果即收敛。整个模型共有壳单元5 832个，梁单元1 128个（图3）。

以一结构方案为例，通过ANSYS谐响应计算，得到加载点在载荷方向（10～200 Hz）间隔1 Hz的加速度频响曲线（图4）。由图可见，首个峰值点处频率为166 Hz，而在模态计算中，此结构的一阶弯曲模态频率也是166 Hz。在优化参数取值范围内，随机选取多组不同参数的结构进行计算，其频响曲线与图4的形式类似，都有一个较大的峰值，峰值频率与结构一阶弯曲模态频率对应。优化中，提取ANSYS迭代计算的加速度频响曲线峰值处频率作为结构一阶弯曲模态频率。

2 加筋圆锥壳振动优化数学模型及求解方法

2.1 设计变量

对于1.1节确定的基本参数，在进行优化设计时，为了减少设计变量的个数，将编号9～12的参数取固定值，即圆锥壳长度L=6 000 mm，艏端半径R=2 000 mm，艉端半径r=500 mm，肋距l=600 mm。对部分变量进行关联处理：环筋与纵筋面板宽度取腹板高度的1/3，面板厚度比腹板厚度大4 mm。最终，将表1中编号1～8的参数作为设计变量，如表2所示，共可得到4 608种结构方案。

表2 设计变量取值空间Table 2 The value space of the design variable

表2中的x6为锥壳板厚组合方案。将壳板厚度分为3段，分别为t1（0～3号肋位）、t2（3～6号肋位）和t3（6～10号肋位），每段板厚可以在［14 16 18］范围内取不同的值。将所有板厚进行全排列组合，共得到27组板厚方案，考虑到工程实际情况：1）相邻两段板厚差小于3 mm；2）艉部段的板厚小于等于艏部段的板厚，即t3≤t2≤t1，最终的锥壳板厚组合方案为8种，如表3所示。

表3 板厚组合Table 3 The combination of shell thickness

2.2 约束条件

将加筋圆锥壳结构重量作为约束条件，约束方程为

式中：W为重量；Wtarget为目标重量。在2.1节的设计变量范围内，结构的重量范围为8.38～14.53 t。

2.3 目标函数

优化目标函数有2个：一是加筋圆锥壳结构第1阶总体弯曲模态频率极大化；二是载荷施加位置处垂向加速度响应总级极小化。

2.4 优化数学模型

为了将问题研究得更加透彻，将优化分为2个层次：一是单目标优化，分别以第1个目标和第2个目标作为目标函数进行单目标优化；二是多目标优化，采用宽容排序法［10］进行优化。

1）单目标优化数学模型。

第1次单目标优化：

第2次单目标优化：

式中，f1(X)和f2(X)分别为加筋圆锥壳结构的第1阶总体弯曲模态频率和载荷施加位置处的垂向加速度响应总级。

2）多目标优化数学模型。

采用宽容排序法进行多目标优化，将各分目标按重要程度进行顺序。

首先，对第1个优化目标进行有重量约束的优化：

在找到第1个优化目标的最优值后，根据宽容排序法的宽容准则设置宽容度，即将第1个优化目标的最优值酌情适当放宽，以作为下一轮优化的约束条件，然后继续对第2个优化目标进行优化。优化数学模型如下：

式中：δ为宽容度，0＜δ＜1；fW为谐响应分析中的扫频间隔，取fW=1 Hz；ai为加速度；a0为基准加速度，a0=10-6m/s2。

2.5 优化求解方法

基于Matlab平台，编写采用遗传算法与宽容排序法的优化主控程序，其中遗传算法中的选择概率取0.9，交叉概率取0.8，变异概率取0.01，设置种群数为50，代数为10（参数设置已经过收敛性分析）。

程序的运行过程如下：要优化主控程序，首先需根据设计变量的取值范围，采用遗传算法生成初始种群，并将相应的结构参数传递给有限元程序ANSYS进行结构响应分析；完成有限元分析后，将结果传递给优化主控程序，优化主控程序根据收敛条件判断程序是否终止，收敛条件为连续5代优化结果相同；若不终止，则优化主控程序根据遗传算法通过选择、交叉和变异操作生成新的种群，然后继续将新的结构参数传递给有限元程序，如此反复，直到优化程序终止。程序运行的流程图如图5所示。

3 加筋圆锥壳结构振动优化结果分析

3.1 弯曲模态频率单目标优化

对结构第1阶总体弯曲模态频率极大化进行无约束单目标优化。共计算了156个个体，占总方案数的3.4%，达到了收敛要求，优化方案的部分结果如表4所示。

分析优化结果，可知结构的第1阶总体弯曲模态频率最大值为185 Hz，对应有2种不同的方案，即方案1-1和方案1-2，这2种方案只是壳板厚度有差异，方案1-1的壳板厚度为［18 16 14］，方案1-2的壳板厚度为［18 16 16］。方案2-1，2-2和2-3以不同的设计参数达到了相同的第1阶总体弯曲频率。上述结果可为工程方案选择提供较大的余地。

3.2 加速度总级单目标优化

在结构第1阶总体弯曲模态附近频段内，对施加垂向载荷处的垂向加速度总级极小化进行无约束单目标优化。共计算了169个个体，占总方案数的3.7%，达到了收敛要求，优化方案的部分结果如表5所示。

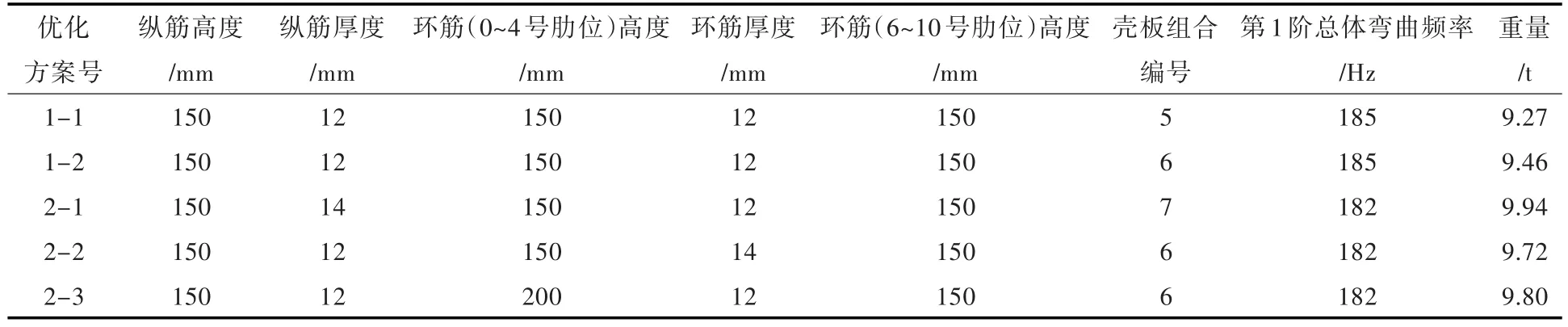
表4 第1阶总体弯曲模态频率单目标优化结果Table 4 Results of overall bending mode frequency optimization

表5 加速度总级单目标优化结果Table 5 Results of acceleration level optimization

通过分析表5的优化结果可知，最优解即方案3的纵、环筋高度以及纵、环筋厚度和壳板厚度均取得最大值，也即结构重量最大的方案。方案4-1，4-2，4-3和4-4以不同的设计参数达到了相同的加速度总级，为工程方案的选择提供了很大的设计空间。

3.3 多目标优化

在结构弯曲模态频率单目标优化结果中，设计变量的取值均接近于设计空间中的最小值，而在载荷处加速度总级单目标优化结果中，设计变量的取值均接近于设计空间中的最大值，即极大化结构第1阶弯曲模态频率与极小化载荷处，加速度响应总级这2种优化方案中的参数取值趋势相异，这为多目标优化提供了优化基础。

由单目标的优化结果可知，结构第1阶总体弯曲模态的频率最大值为185 Hz。在此基础上，设置0.05的宽容度，设置目标重量Wtarget=12 t，进行多目标优化。共计算了152个个体，占总方案数的3.3%，达到了收敛要求，优化方案的部分结果如表6所示。表中，方案5～7为满足约束条件的优化方案中加速度总级最小的3个方案，其中方案5为最优解。

将多目标优化最优方案与前面所述的2种单目标优化最优方案进行对比，结果如表7所示。

分析表7的优化结果可知，与2种单目标优化结果相比，多目标优化方案满足了宽容度的限制，在各个参数的取值上没有像单目标优化结果中那样较多地取上限或者是下限，并且其同时存在几组结构第1阶总体弯曲频率、结构重量和加速度总级都比较接近的设计方案，便于工程应用上综合考虑后选用。

表6 多目标优化结果Table 6 Results of muti-object optimization

表7 单目标与多目标优化结果对比Table 7 Comparison of single-object and multi-object optimization results

4 重量约束与宽容度对优化结果的影响

为了进一步研究宽容度以及重量约束条件对结构优化结果的影响，分别设置目标重量Wtarget=12，11和 10 t，设置宽容度分别为 0.025，0.05，0.1，0.15和0.2，群体规模仍为50×10。取优化结果中的最优方案进行对比，结果分别如表8～表10所示。

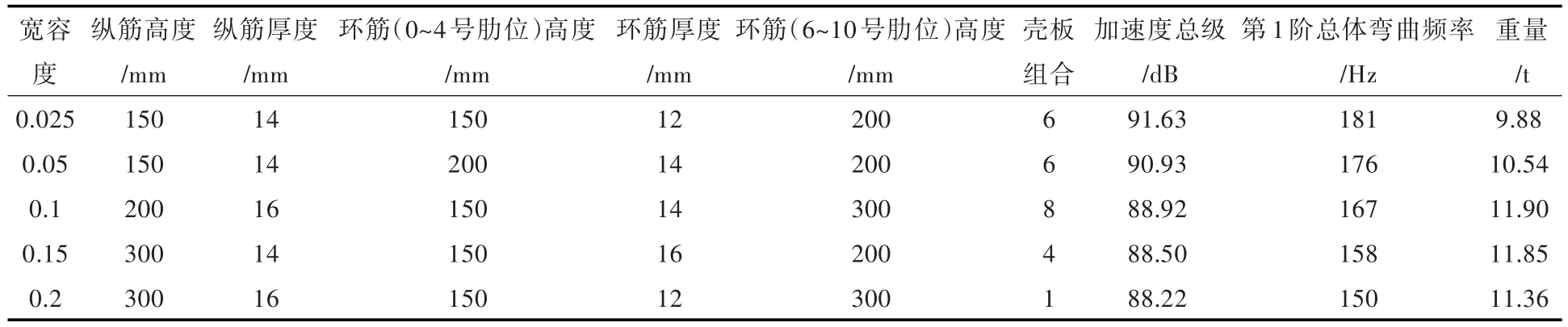
表8 12 t重量约束下不同宽容度优化结果Table 8 Optimization results under different tolerances at 12 t weight constraint

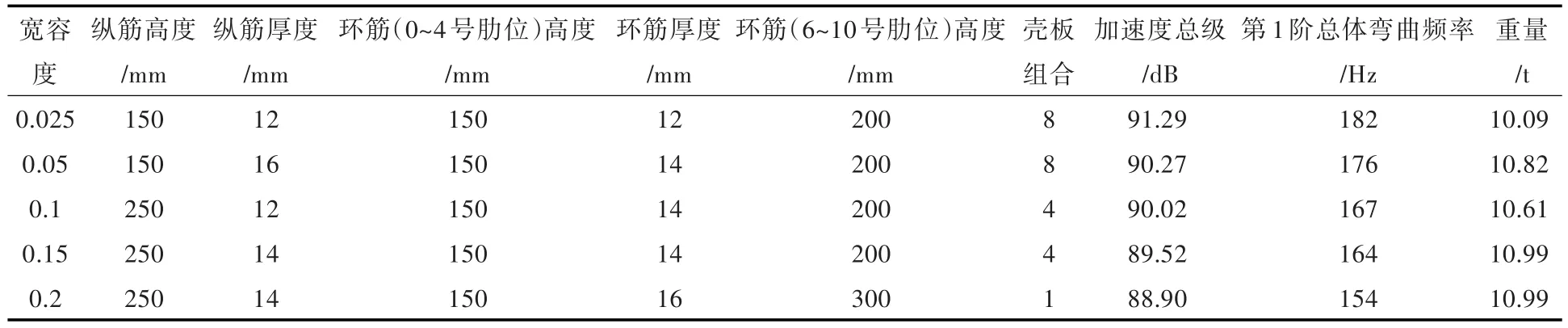
表9 11 t重量约束下不同宽容度优化结果Table 9 Optimization results under different tolerances at 11 t weight constraint

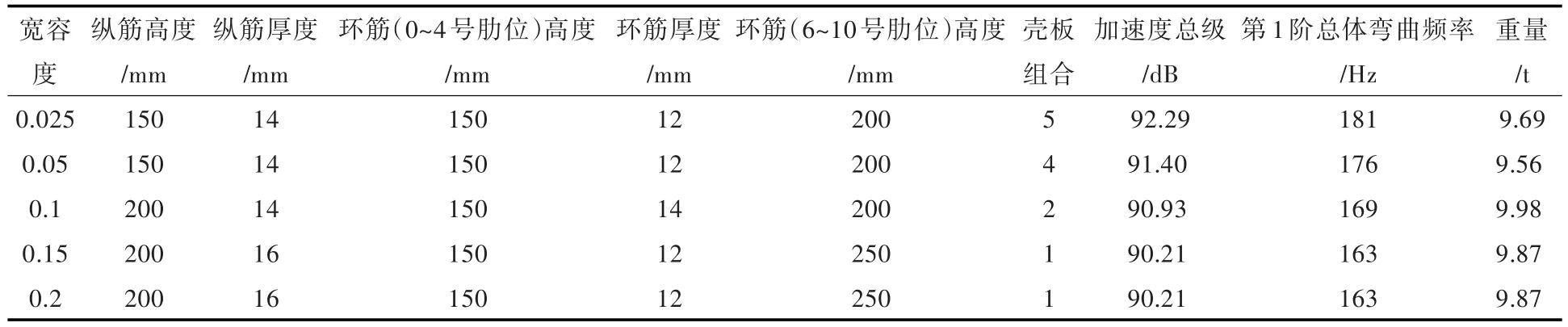
表10 10 t重量约束下不同宽容度优化结果Table 10 Optimization results under different tolerances at 10 t weight constraint

分析表8～表10中数据可知：

1）在相同的重量约束条件下，当结构的第1阶总体弯曲频率较大，即宽容度较小时，最优方案载荷处的加速度总级较大；当结构的第1阶总体弯曲频率较小，即宽容度较大时，最优方案载荷处的加速度总级较小。

2）在相同的宽容度下，载荷处的加速度总级基本呈随目标重量的增大而减小的趋势。

为了更直观、清晰地表示变化趋势，以宽容度、目标重量和载荷处加速度总级为x，y，z轴，绘制三维图（图6）。

5 结 论

本文采用遗传算法和宽容排序法，对纵横加筋圆锥壳的振动特性进行了多目标优化求解，主要结论如下：

1）在结构第1阶总体弯曲频率单目标优化的最优与次优方案中，结构纵、环筋设计变量的取值均为设计空间中的较小值；在载荷处加速度响应总级单目标优化的最优与次优方案中，结构设计变量的取值均为设计空间中的较大值。在2个单目标优化的优化方案中，设计参数的取值趋势相异，为多目标优化提供了优化基础。在本文的算例中，单目标优化同一个目标值，可以有多个方案与之对应，这为工程设计提供了多种选择。

2）随着宽容度以及目标重量的增大，最优方案结构载荷处的加速度总级减小；随着宽容度以及目标重量的减小，最优方案结构载荷处的加速度总级增大。目标重量和宽容度的设置在工程上具有明确的意义。

3）获得本文算例优化解的计算方案数占总方案数的3.3%～4.8%，说明提出的优化设计数学模型具有较高的效率。

［1］LIU M，LIU J，CHENG Y S.Free vibration of a fluid loaded ring-stiffened conical shell with variable thickness［J］.Journal of Vibration and Acoustics，2014，136（5）：051003.

［2］LIU J，YE X，LIU M，et al.A semi-analytical method of free vibration of fluid loaded ring-stiffened stepped conical shell［J］.Journal of Marine Engineering&Technology，2014，13（2）：35-49.

［3］WANG X Z，WU W G，YAO X L.Structural and acoustic response of a finite stiffened conical shell［J］.Acta Mechanica Solida Sinica，2015，28（2）：200-209.

［4］周云泽，赵应龙.简支截顶圆锥壳固有振动特性分析及仿真验证［J］. 舰船科学技术，2016，38（3）：45-49.ZHOU Y Z，ZHAO Y L.The natural vibrational characteristics of simply supported truncated conical shells and the simulation verification［J］.Ship Science and Technology，2016，38（3）：45-49（in Chinese）.

［5］陈美霞，谢坤，魏建辉.带框架肋骨圆柱壳振动特性分析［J］.华中科技大学学报（自然科学版），2014，42（3）：127-132.CHEN M X，XIE K，WEI J H.Vibration characteristics analysis of cylinder shell with frame rib［J］.Journal of Huazhong University of Science and Technology（Natural Science Edition），2014，42（3）：127-132（in Chinese）.

［6］瞿叶高，华宏星，孟光，等.圆柱壳—圆锥壳组合结构振动分析的新方法［J］. 工程力学，2013，30（3）：24-31.QU Y G，HUA H X，MENG G，et al.A new method for vibration analysis of joined cylindrical-conical shells［J］.Engineering Mechanics，2013，30（3）：24-31（in Chinese）.

［7］肖伟，程远胜，曾广武.纵横加筋圆柱壳结构的多目标优化设计［J］. 中国造船，2004，45（增刊 1）：106-111.XIAO W，CHENG Y S，ZENG G W.Multi-objective optimization design of longitudinal-transverse stiffened cylindrical shell［J］.Shipbuilding of China，2004，45（Supp 1）：106-111（in Chinese）.

［8］李学斌，朱学康.潜艇耐压圆柱壳的多目标优化设计［J］. 中国造船，2009，50（1）：10-18.LI X B，ZHU X K.Multi-objective optimization design of circular cylindrical ring-stiffened shell of submarine［J］.Shipbuilding of China，2009，50（1）：10-18（in Chinese）.

［9］叶文荣，张恒，缪旭弘，等.多点激励力下圆柱壳振动响应优化设计［J］.噪声与振动控制，2013，33（2）：36-39.YE W R，ZHANG H，MIAO X H，et al.Design of cylindrical shell for dynamic performance optimization under multi-excitations［J］.Noise and Vibration Control，2013，33（2）：36-39（in Chinese）.

［10］曾广武.船舶结构优化设计［M］.武汉：华中科技大学出版社，2004：72-78.