粒子群算法在约束型垫高阻尼结构动力学优化中的应用

易少强，何世平，王杰

海军工程大学动力工程学院，湖北武汉430033

0 引 言

随着现代科学技术的发展，振动、噪声和冲击的控制日益成为一个复杂而迫切的问题［1］。为此，各国学者一直致力于机械系统的减振降噪。其中，基于垫高层的设计理念，是在传统约束型阻尼结构的基层与阻尼层之间加上垫高层，其能杠杆放大阻尼层的剪切变形，改善结构的损耗因子。垫高层材料可以采用蜂窝状或蓬松的硬泡沫，该材料能显著降低结构的整体质量，因此被广泛应用于航空航天和交通运输等领域的减振降噪工程中。

随着对约束型垫高阻尼结构研究的不断深入，国内外学者在动力学建模、参数分析以及优化设计等方面取得了许多成果。Falugi［2］对约束型垫高阻尼结构的减振机理进行了分析，并进行了实验验证。Rogers等［3］对约束型垫高阻尼结构试样梁进行了参数研究，结果表明，在垫高层厚度增加20%的情况下，振动响应的幅值降低16.4%。Huang等［4］对约束型垫高阻尼梁进行了振动实验，证明使用微孔泡沫作为垫高层可以将振幅降低80%。Chaudry等［5］分别利用传递函数法和有限元法建立了约束型垫高阻尼结构的动力学方程，同时，通过对分段和未分段约束型垫高阻尼结构进行频率响应分析，验证了理论模型的有效性。燕碧娟等［6］针对农业机械中的管状过渡阻尼结构，使用ANSYS子问题逼近法进行了参量优化。随后，燕碧娟等［7］利用分布参数传递函数法对层间过渡约束阻尼悬臂板进行动力学响应特征分析，探讨了过渡层参数对动力学特性的影响。

约束型垫高阻尼结构在理论和工程应用方面越来越成熟，然而结构振动级的要求也越来越严格，为使约束型垫高阻尼结构各项性能指标达到最佳，需要对其动力学性能进行优化。传统的优化策略往往是针对连续域变量，获得的最优解的实用性有待商榷，特别是当拥有最优解属性的材料不容易获得或难以研制出来时，该优化结果对实际工程的指导意义不大。为此，本文拟通过改进通用性和有效性较佳的粒子群算法，来对约束型垫高阻尼结构连续域变量（结构厚度）和离散域变量（材料类型）进行优化设计，以期将获得的最优解直接用于指导约束型垫高阻尼结构的设计。

1 约束型垫高阻尼结构动力学模型

1.1 基本假设条件

约束型垫高阻尼板的物理模型如图1所示，包含约束层、阻尼层、垫高层和基层，其中H1，H2，H3和H4分别表示基层、垫高层、阻尼层和约束层上表面到基层中面的距离。基于如下假设条件对其进行动力学分析［8］：

1）阻尼结构服从小变形理论，且同一截面任一点具有相同的横向位移。

2）各层之间无相对滑移，层间位移保持连续性。

3）垫高层和阻尼层主要发生剪切变形。

4）基层和约束层的几何关系满足Kirchhoff假设，其剪切效应小。

5）忽略各层转动惯量的影响。

1.2 本构关系

根据薄板弯曲理论，可以得到各层板内任一点的位移：

式中：h2和h3分别为垫高层与阻尼层厚度；u，v，w分别为基层和中面沿x，y，z方向的位移；U，V，W为各结构层内任一点沿x，y，z方向的位移；αx和αy分别为垫高层沿x轴和y轴方向的剪切变形；βx和βy分别为阻尼层沿x轴和y轴方向的剪切变形。

在微小位移和微小变形情况下，根据应变—位移关系，可以得到各层板内任一点的应变：

式中：εx和εy分别为沿x轴和y轴方向的应变；γxy为切应变。根据广义胡克定律，可以得到各层的应力—应变关系：

式中：σx和σy分别为沿x轴和y轴方向的应力；τxy为切应力；E为弹性模量；υ为泊松比。

1.3 能量方程

根据薄板弯曲理论和能量原理，可得约束型垫高阻尼结构势能的表达式为：

式中：UE为拉伸变形和弯曲变形贡献的势能；UG为剪切变形贡献的势能；G2为垫高层剪切模量；G3为阻尼层剪切模量；Δ为单元的位移向量；KE为发生拉伸和弯曲变形单元的刚度矩阵；KG为发生剪切变形单元的刚度矩阵。约束型垫高阻尼结构的刚度矩阵的表达式为

约束型垫高阻尼结构动能的表达式为：

式中：Tu为拉伸变形贡献的动能；Tw为弯曲变形贡献的动能；ρi为各层密度；Mu为发生拉伸变形单元的质量矩阵；Mw为发生弯曲变形单元的质量矩阵。约束型垫高阻尼结构刚度矩阵的表达式为

根据Hamilton变分原理，得到约束型垫高阻尼板的动力学方程为

式中：为加速度；X为位移向量；F为外部激励载荷向量。

利用模态应变能法求解时，将自由振动解代入式（12），得到特征方程：

式中，ω*为角频率复数形式的特征值。

求解式（13），得到约束型垫高阻尼板各阶模态频率和损耗因子：

2 约束型垫高阻尼结构的优化

2.1 粒子群算法

粒子群算法是由 Kennedy等［9］和Eberhart等［10］于1995年提出的一种仿生优化计算方法。算法通过模拟自然界生物群体行为，将每个潜在解比拟为某个群体中的个体，这些个体被称为“粒子”。粒子之间存在信息交流和协作机制，使整个群体有序地向可能解方向演化，直至找到最优解。

设D维目标搜索空间中，种群粒子个数为N，其中第i个粒子的位置和速度分别为x=在每次迭代寻优过程中，根据适应度值的大小评价各粒子的优劣，确定粒子目前的最佳位置pbest和群体目前的最佳位置gbest。通过跟随这两个最佳位置，然后根据式（16）和式（17）对粒子进行更新操作［11］。

式中：λ为惯性权重，c1和c2为学习因子；r1和r2为［0，1］之间均匀分布的随机数，控制粒子飞行的随机性。为了防止粒子盲目地搜索最优解区域，需对粒子位置和速度区间进行控制，如果粒子的位置和速度超过阈值，则可以让粒子的位置和速度取边界值。

2.2 改进的粒子群算法

约束型垫高阻尼结构的优化设计包括结构层厚度及材料类型的优化，其中结构层厚度的优化属于连续域的优化问题，结构层材料类型的优化属离散域的优化问题。考虑到粒子群算法在连续域变量优化以及离散域变量优化（任务分配［12］、路径规划［13］、车间调度［14］等）方面的通用性和有效性，对粒子群算法中的粒子更新机制进行改进，以解决该组合优化问题。

为有效求解材料类型优化配置的离散域问题，以背包问题为背景，通过改进粒子群算法的离散机制及更新机制，达到优化设计的目的。对材料类型的设计变量采用正整数编码的方式，设有s个设计变量，且含有n1个离散变量，n2个连续变量，则种群中第i个粒子表示约束型垫高阻尼结构的设计变量为，其中xi,j表示初始种群粒子的位置，j=1,2,…,n1，n为材料类型的数目，当xi,j=1时表示采用第1种材料，当xi,j=n时表示采用第n种材料。因此，这样的编码方式能较好地表达各结构层采用的材料类型。针对种群中反映材料类型的位置的更新问题，将利用式（17）得到的新材料类型的位置与其编号集合中的每一个元素作差，并取绝对值，然后逐一进行排序，最后提取最小绝对值所对应的元素作为此次更新后所选择的材料类型。通过Matlab实现的主要程序代码为：

其中：nk为材料类型集合中的任意元素，该离散化处理不同于向上取整或向下取整，而是逐渐逼近离散值，更有利于快速、准确地求解优化问题；为第t代种群粒子的位置；abs表示函数取绝对值；sort表示函数按照升序排列；consort和index为可以任意赋值的变量。

2.3 算法的基本流程

优化约束型垫高阻尼结构的粒子群算法的基本流程如图2所示，其主要步骤［15］如下。

1）粒子位置和速度的初始化。种群中的各粒子代表相应的设计变量，由此可以根据垫高阻尼结构的设计变量来确定优化问题的维数以及种群粒子的个数。在Matlab中实现种群中各粒子速度和位置初始化的主要程序代码如下：

其中：rands表示在［-1，1］区间均匀分布的随机数；unidrnd表示产生的随机离散整数；rand表示在［0，1］区间均匀分布的随机数；xmin和xmax分别为各连续变量的下限值和上限值。取初始位置为粒子最佳位置pbest。

2）群体最佳位置的选择。调用ANSYS有限元模型，得到模态参数，代入适应度函数评价群体各粒子的优劣，并与粒子目前的最佳位置pbest对比，挑选更优者作为群体最佳位置gbest。

3）速度和位置的更新。根据式（16）和式（17）以及排序取整原则代码，更新粒子的速度和位置。

4）粒子最佳位置的更新。再次调用有限元模型，得到模态参数，代入适应度函数评价新群体各粒子的优劣，并与粒子目前的最佳位置pbest对比，挑选更优者作为粒子的最佳位置pbest。

5）群体最佳位置的更新。将新群体各粒子的适应度值与群体目前的最佳位置gbest进行对比，挑选更优者作为群体的最佳位置gbest。

6）终止条件的判断。终止条件通常有2种方式：一种方式是预设寻优代数，当寻优代数达到设置的最大值时，结束搜索；另一种方式是指定运算精度，当搜寻的最优值与问题最优值的误差小于运算精度时，结束搜索［16］。选择第1种方式，若满足条件，则寻优结束，输出结果，否则返回步骤3），继续搜索。

2.4 数学模型优化

为进一步优化约束型垫高阻尼结构的振动特性，仍以前5阶模态损耗因子的最佳化为目标函数，以各结构层厚度、材料类型为设计变量，阻尼处理的附加厚度、附加质量为状态变量，则优化问题的数学模型为：

式中：η0i为初始结构的第i阶模态损耗因子；ηi为优化配置后结构的第i阶模态损耗因子；h1为初始结构基层厚度，h4为优化配置后的约束层厚度；m1为初始结构基层质量，m2，m3和m4分别为优化配置后的垫高层、阻尼层和约束层质量；为约束系数，其中κ1为附加厚度约束系数，用于限制阻尼处理的厚度，κ2为附加质量约束系数，用于限制阻尼处理的质量，取引入初始结构前5阶模态损耗因子η0i的目的是使目标函数无量纲化。

2.5 算例分析

约束型垫高阻尼结构的初始模型选择四边简支阻尼板，基本参数包括：基层长度为0.3 m，宽度为0.2 m；基层、垫高层和阻尼层的厚度均为3 mm，约束层厚度为1 mm；基层和约束层采用钢材料，弹性模量为2.06×1011Pa，密度为7 800 kg/m3，泊松比为0.30；垫高层采用Dyad606材料，弹性模量为 2.9×108Pa，密度为 1 200 kg/m3，泊松比为0.35；阻尼层材料采用文献［17］中的粘弹性阻尼材料，弹性模量为6×107Pa，密度为1 140 kg/m3，泊松比为0.49，材料损耗因子为0.65。通过ANSYS软件进行仿真计算，得到初始结构前5阶模态频率和损耗因子，结果如表1所示。

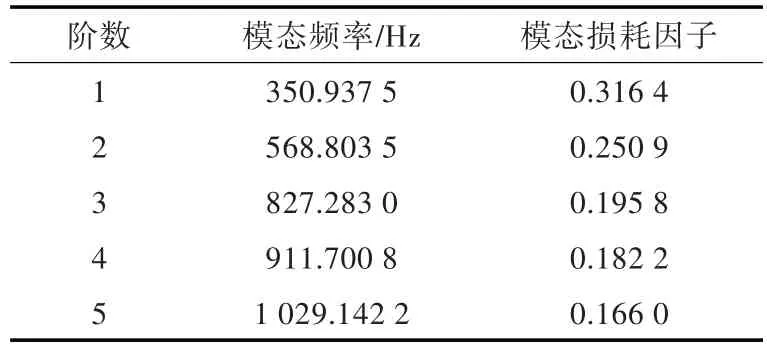
表1 初始结构前5阶模态频率和损耗因子Table 1 The first five modal frequencies and loss factors of the initial structure

对材料类型进行优选时，可供选择的垫高层、阻尼层和约束层的材料类型如表2所示。

考虑变量优化的维度以及效率，粒子群算法的参数设置如下：种群个数为30，最大迭代次数为30。为了使算法迭代初期有较大的全局搜索能力，迭代后期有较强的局部搜索能力，本文采用非线性的惯性权重和学习因子，其数学表达式为：

式中：λmax=0.9，λmin=0.4，分别为惯性权重的最大值和最小值；cmax=2，cmin=0.5，分别为学习因子c1的最大值和最小值；，分别为学习因子c2的最大值和最小值；d和Imax分别为当前迭代次数和最大迭代次数。

算法迭代搜索最优解区域的进程如图3所示。由图3可知，随着迭代寻优的递进，各代种群的最佳适应度随之下降，当迭代达到12次时适应度趋于稳定。这证明了算法的收敛性，且能快速、准确地得到约束型垫高阻尼结构的优化结果。

约束型垫高阻尼结构的优化结果如表3所示。由表3可以看出：由于粒子群算法迭代寻优时具有一定的随机性，且考虑到设置的算法最大迭代次数有限，所以连续5次优化后搜索得到的群体最佳位置gbest会在最优值附近发生轻微的浮动。将第1次优化配置后的约束型阻尼结构与初始结构进行对比发现：其附加厚度增加了28.56%，附加质量减小了23.35%；前5阶模态损耗因子和初始结构相比分别提高了2.69%，18.29%，29.88%，32.71%和36.02%，前5阶模态频率和初始结构相比分别增加了32.77%，29.94%，26.51%，25.57%和24.41%；同时可以看出，随着模态阶数的增加，前5阶模态损耗因子的变化率随之增加，而前5阶模态频率的变化率则随之减小，说明该优化对高阶模态损耗因子的改善效果更好。

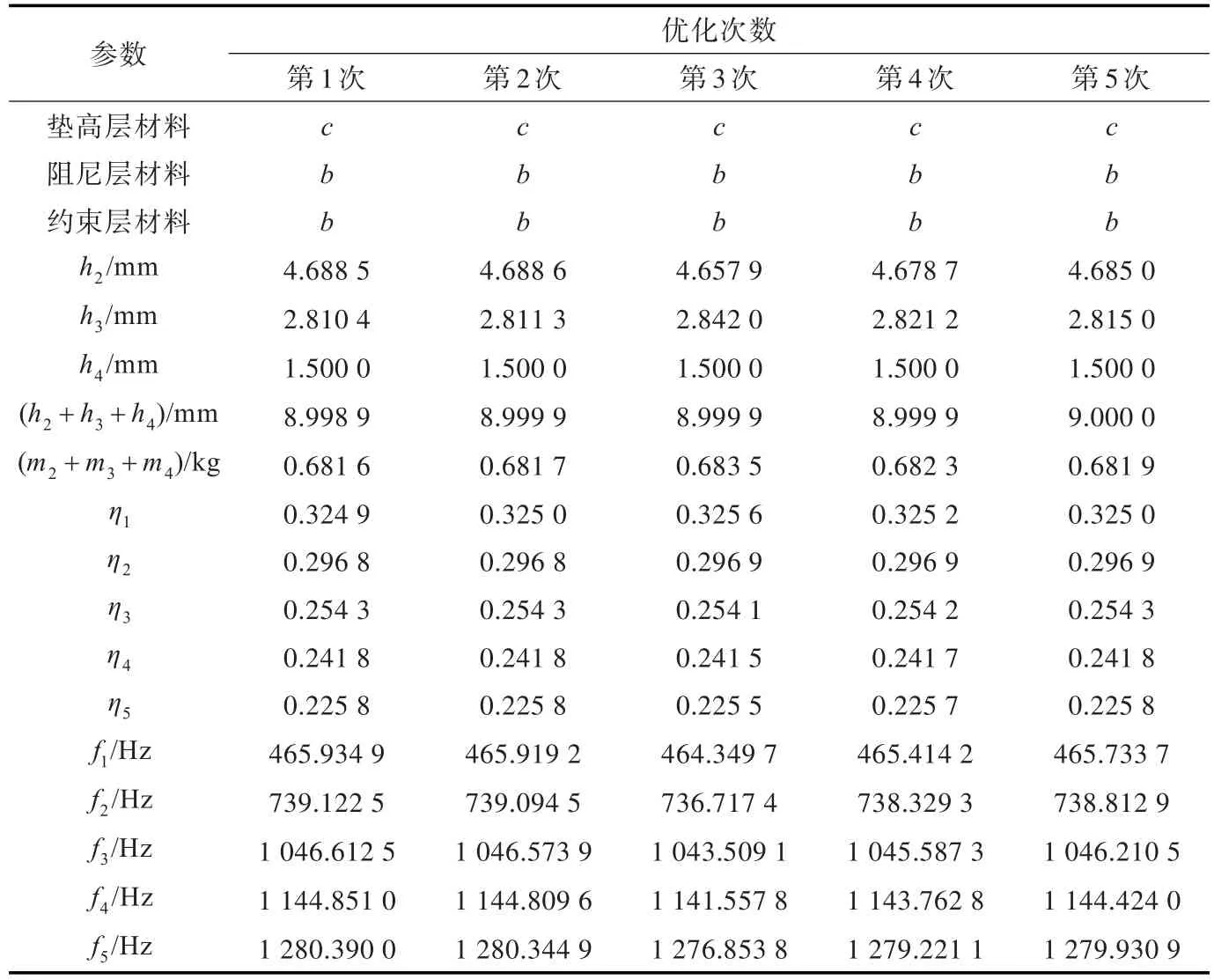
表3 约束型垫高阻尼结构的优化结果Table 3 Optimization results of constrained stand-off layer damping structure

3 结 论

针对约束型垫高阻尼结构含连续变量（结构厚度）和离散变量（材料类型）的优化问题，本文通过改进粒子群算法，利用Matlab调用ANSYS有限元模型及两者间数据的传递，实现了对约束型垫高阻尼结构的动力学优化，从而能保证结构振动特性达到最佳。

1）采用改进的粒子群算法能快速、有效地实现约束型垫高阻尼结构的动力学优化，不仅充分发挥了结构的阻尼特性，而且最大限度地减少了附加质量的引入，满足了结构轻量化的设计原则，同时对材料类型的优选可以直接应用于工程设计，具有一定的工程指导意义。

2）利用改进的粒子群算法和ANSYS有限元软件进行联合仿真，能有效实现结构的优化设计。但粒子群算法只是智能算法的一种，后续可进一步研究应用其他智能算法进行约束型垫高阻尼结构的动力学优化，以实现高效、可靠的优化。

［1］刘棣华.粘弹阻尼减振降噪应用技术［M］.北京：宇航出版社，1990.

［2］FALUGI M.Analysis of a five layer viscoelastic constrained layer beam［C］//Proceedings of Damping'91.San Diego，United States：Wright Laboratory，1991：2.

［3］ROGERS L C，PARIN M.Experimentalresultsfor stand-off passive vibration damping treatment［C］//Proceedings of the SPIE 2445，Smart Structures and Materials 1995：Passive Damping.San Diego，United States：SPIE，1995：374-383.

［4］HUANG P Y H，REINHALL P G，SHEN I Y，et al.Use of microcellular foam materials in constrained layer damping treatments［J］.Cellular Polymers，2001，20（2）：101-114.

［5］CHAUDRY A，BAZ A.Vibration control of beams using stand-off layer damping：finite element modeling and experiments［C］//Proceedings of the SPIE 6169，Smart Structures and Materials 2006：Damping and Isolation.San Diego，United States：SPIE，2006：61690R.

［6］燕碧娟，孙大刚，张文军，等.农业机械管状过渡阻尼结构参数分析及优化［J］.农业工程学报，2015，31（22）：56-62.YAN B J，SUN D G，ZHANG W J，et al.Parameter analysis and optimization of tubular transitional layer damping structure for agricultural machinery［J］.Transactions of the Chinese Society of Agricultural Engineering，2015，31（22）：56-62（in Chinese）.

［7］燕碧娟，张文军，李占龙，等.层间过渡约束阻尼结构动力响应的分布参数传递函数解［J］.振动与冲击，2016，35（5）：186-190，233.YAN B J，ZHANG W J，LI Z L，et al.Distributed parameter transfer function method for dynamic response of a constrained damping structure with transition layer［J］.Journal of Vibration and Shock，2016，35（5）：186-190，233（in Chinese）.

［8］李攀.约束阻尼结构动力学拓扑优化方法研究［D］.重庆：重庆大学，2013.

［9］KENNEDY J，EBERHART R.Particle swarm optimization［C］//Proceedings of 1995 IEEE International Conference on Neural Networks.Perth，Australia：IEEE，1995：1942-1948.

［10］EBERHART R，KENNEDY J.A new optimizer using particle swarm theory［C］//Proceedings of the 6th International Symposium on Micro Machine and Human Science.Nagoya，Japan：IEEE，1995：39-43.

［11］余胜威.MATLAB优化算法案例分析与应用［M］.北京：清华大学出版社，2014.

［12］张琪新，孙富春，许斌，等.基于离散粒子群算法的多飞行器在轨服务任务分配［J］.中国空间科学技术，2012，32（2）：68-76.ZHANG Q X，SUN F C，XU B，et al.Multiple spacecrafts on-orbit service task allocation based on DPSO［J］.Chinese Space Science and Technology，2012，32（2）：68-76（in Chinese）.

［13］王慧，王光宇，潘德文.基于改进粒子群算法的移动机器人路径规划［J］.传感器与微系统，2017，36（5）：77-79.WANG H，WANG G Y，PAN D W.Mobile robot path planning based on modified particle swarm optimization algorithm［J］.Transducer and Microsystem Technologies，2017，36（5）：77-79（in Chinese）.

［14］陈明，胡言乐，刘晋飞.基于粒子群算法的多目标柔性作业车间调度问题研究［J］.机电一体化，2017，23（1）：11-15，60.CHEN M，HU Y L，LIU J F.Multi-objective flexible job-shop scheduling problem based on particle swarm optimization［J］.Mechatronics，2017，23（1）：11-15，60（in Chinese）.

［15］高芳.智能粒子群优化算法研究［D］.哈尔滨：哈尔滨工业大学，2008.

［16］龚纯，王正林.精通MATLAB最优化计算［M］.北京：电子工业出版社，2009.

［17］施磊.车身壁板多孔阻尼优化与车内噪声控制［D］.重庆：重庆大学，2012.