后艉轴承刚度对潜艇结构振动与声辐射的影响
2018-02-26王路才周其斗杨常青
王路才,周其斗,杨常青
1海军大连舰艇学院航海系,辽宁大连116018
2海军工程大学舰船工程系,湖北武汉430033
0 引 言
潜艇在水下航行时,其声频信号是敌方探测和打击的重要信号,因而声隐身技术一直受到各国海军的高度重视[1-2]。了解潜艇的噪声辐射机理,并在设计阶段研究其减振降噪措施、预估其减振降噪效果,是提高潜艇声隐身性能的有效途径。
潜艇航行时,由于艉流场的不均匀性,螺旋桨除了提供推力驱动潜艇前进外,还会产生不定常激励力作用在艇体结构上,这是引起艇体振动的重要激励源[3]。由螺旋桨不定常激振力诱发的艇体结构辐射声是潜艇水下辐射噪声的重要组成部分,也是潜艇减振降噪领域的一个综合性难题。螺旋桨不定常激励力主要包含沿艇体轴线方向的轴向激振力和垂直于艇体轴线方向的径向激振力。轴向激振力主要通过艉轴和推力轴承传递到推力轴承基座上,进而激起艇体结构的振动与声辐射,且一般发生在中、高频。径向激振力主要通过艉轴和艉轴承传递到艉轴承支座上,进而激起艇体结构的振动和声辐射。对于潜艇结构而言,由螺旋桨径向激振力引起的艇体结构振动和声辐射主要发生在低频段,对潜艇水下航行的声隐身性能影响较大。
目前针对螺旋桨轴向激振力引起的艇体结构振动与声辐射的研究较多[4-7],并建立了相关计算方法和控制措施。而对螺旋桨径向激振力引起的艇体结构振动和声辐射的重视程度不够,相关研究较少,研究集中在轴系的横向振动特性上,主要包括轴承刚度、轴承支撑长度及间距等对船舶轴系振动特性的影响[8-10],且一般关注点为轴承的润滑性能,并没有深入到对潜艇艇体振动和声辐射的层面。
轴承是轴系与艇体的连接结构,也是激振力与振动传递的中间环节。螺旋桨径向激振力对艇体结构的激励作用主要通过轴系及相关轴承结构传递到艇体上[11]。轴承的结构参数既影响轴系的振动,也对轴系振动向艇体的传递产生影响,如何通过改变轴承结构参数,在传递路径上控制振动的传递,达到减振降噪的目的,是值得研究的问题。
本文将采用SUBOFF艇型,建立包含螺旋桨和轴系实体结构单元的潜艇整艇结构模型,采用通用有限元程序NASTRAN计算其在真空中的振动特性,并采用附加质量附加阻尼算法计算其在水下的振动和声辐射特性。通过计算潜艇整艇结构在螺旋桨垂向激振力作用下的振动与声辐射特性,着重考虑后艉轴承刚度对潜艇整艇结构振动与声辐射的影响规律,为在声学设计阶段潜艇关键部位结构参数的选取提供参考。
1 潜艇整艇结构建模
SUBOFF潜艇模型是美国国防部高级研究计划署(Defence Advanced Research Projects Agency,DARPA)资助的 SUBOFF 计划所使用的模型[12]。本文模型在标准模型的基础上进行缩比,并参考现有SUBOFF试验模型艇,缩比后整艇艇长为9.91 m(螺旋桨尾部至艇艏),螺旋桨采用通用的五叶桨。本文采用MSC.PATRAN软件对缩比后的SUBOFF潜艇整艇模型进行有限元建模,其中艇体结构主要采用三角形面单元和四边形面单元,对艇体结构中的加强筋和肋骨等采用梁单元建模,前艉轴承和推力轴承采用刚性MPC连接模拟,同时为了尽可能反映潜艇真实振动情况,螺旋桨和轴全部采用体单元建模,依据后续自编流固耦合计算软件的要求,潜艇湿表面结构采用3节点三角形单元形式。
由于潜艇模型激振力施加在螺旋桨中心处,因而螺旋桨的振动比较复杂。为了能够真实反映结构的振动,螺旋桨部分单元尺度取为20 mm,艇体部分单元尺度取为80 mm。
图1~图4为SUBOFF潜艇结构有限元模型,其中图1为SUBOFF潜艇整艇结构有限元模型,图2为隐藏掉湿表面后的整艇内部结构有限元模型,图3为隐藏掉湿表面后整艇艉部结构有限元模型,图4为螺旋桨和轴结构有限元模型。
结构模型螺旋桨部分的材料为镍铝青铜,其余部分的材料为钢,镍铝青铜和钢的材料参数如表1所示。

表1 钢和铜的材料参数Table 1 Parameters of steel and copper
2 附加质量附加阻尼算法
潜艇结构水下振动与声辐射问题是流体与结构相互作用的流固耦合问题。本文采用结构有限元耦合流体边界元的附加质量附加阻尼算法[13-14],计算潜艇整艇结构的水下振动与声辐射。该方法采用由流体到结构进行解耦的方式实现流固耦合问题的解耦。基于此,研发了大型水下结构流固耦合振动与声辐射计算程序,可以通过FORTRAN和DMAP语言混合编程实现流固耦合问题的解耦,并利用通用有限元软件NASTRAN实现大型复杂结构流固耦合振动和声辐射问题的计算[15]。经过与美国学者的声学试验结果进行对比[15-16],验证本文所采用的计算程序的正确性和有效性。
考虑如图5所示的流体与结构相互作用的系统:流体外域Ω0被潜艇结构湿表面S0分开,流体外域中流体密度为ρ0,声速为c0。
对结构域S0,考虑其稳态响应问题,并进行有限元离散,可得
式中:ω为圆频率;KS,MS,CS分别为结构刚度、质量和阻尼矩阵;aˉ为节点位移向量;f为直接作用在结构上的节点力;pout为艇外流体对结构作用的等效节点力。
艇外流体对结构作用的等效节点力可以采用文献[11]与文献[12]所述的方法求得
式中:L为单元匹配矩阵,为艇外流体对结构作用所产生的全局附加质量和附加阻尼矩阵。自由液面的反射影响考虑与否可通过设置不同的格林函数实现[11-12]。
把式(2)代入到式(1)中并简化可以得到流体与结构相互作用的动力方程为
由式(3)可以得到结构位移并提取湿表面上的节点位移,从而得到湿表面法向位移向量U。
由公式
可以得到湿表面的辐射声功率W和均方法向速度式中:为第j号湿表面单元上的压力幅值;为第j号湿表面单元上的法向位移幅值;Sj为第j号湿表面单元的面积;“*”表示取相应量的共轭值;me表示湿表面的个数。
由公式
可以相应地得到辐射声功率级以及均方法向速度级。式中:Wref=10-12W,为辐射声功率的参考值;,为均方法向速度的参考值。
3 真空中后艉轴承刚度对潜艇结构振动的影响
一般而言,艉轴承不限制轴沿艇长方向(x方向)的位移,只限制其在径向方向的位移,即yz方向的位移。本文着重考虑后艉轴承刚度对潜艇整艇结构振动与声辐射的影响,如图6所示。后艉轴承的前端、后端和中部与艉轴之间分3组各采用12个刚度相同的弹簧相连,各组相邻弹簧之间的角度为30°,共36根弹簧。本文中yz方向刚度指螺旋桨轴与艉轴承之间单个弹簧的刚度,如表2所示。本文设置了4种不同的单个弹簧刚度值作为计算工况,分别为yz方向刚性连接,yz方向刚度5.0×107N/m,yz方向刚度5.0×106N/m和yz方向刚度1.0×106N/m,以此来考察不同后艉轴承刚度对潜艇结构振动的影响。
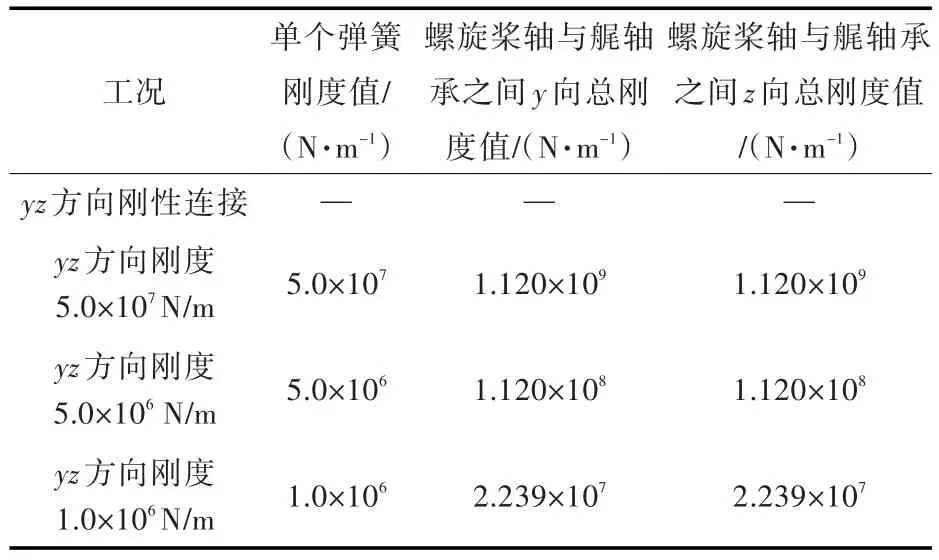
表2 SUBOFF整艇结构在真空中激振的工况设置Table 2 Subcases of the structure of SUBOFF submarine in vacuum
首先采用通用有限元程序MSC.NASTRAN对具有不同后艉轴承刚度的潜艇整艇模型进行模态分析。表3列出了4种工况下模型潜艇的前3阶整体垂向弯曲模态频率。由表3可以看出,随着后艉轴承刚度的减小,模型潜艇的整体垂向弯曲模态频率逐渐降低,尤其第2阶和第3阶整体垂向弯曲模态。
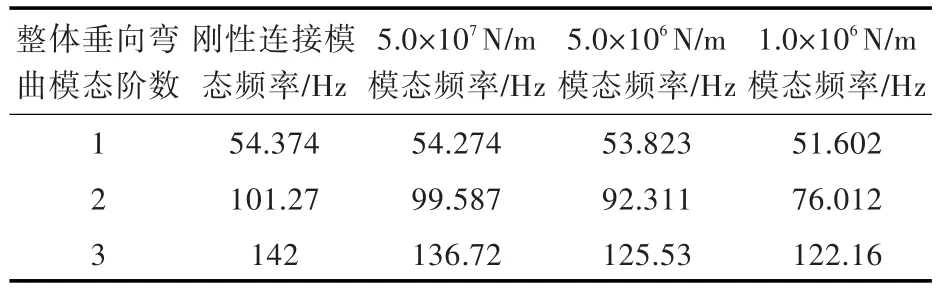
表3 4种工况下模型潜艇的前3阶整体垂向弯曲模态频率Table 3 The first three overall bending modal frequencies of submarine under four subcases
图7列出了yz方向刚性连接情况下模型潜艇的前3阶整体垂向弯曲模态振型。
如图1所示,在模型螺旋桨的中心处施加幅值为100 N的激振力,激振力方向竖直向上(由于后艉轴承并不限制轴沿艇长方向的位移,本文的相关计算分析没有考虑螺旋桨水平方向的激振力),对具有不同后艉轴承刚度的SUBOFF潜艇整艇模型进行结构在真空中(计算时不考虑空气对结构振动的影响,为真空理想状态)的频率响应计算,计算频率步长为:频率范围在10~200 Hz时,步长取1 Hz;频率范围在200~800 Hz时,步长取2 Hz。图8为真空中具有不同后艉轴承刚度的SUBOFF潜艇整艇结构均方法向速度级频响曲线。由图8可以看出,随着艉轴承与轴之间yz方向刚度的减小,SUBOFF潜艇整艇结构均方法向速度级频响曲线的第1个峰值频率基本不变,第2个和第3个峰值频率逐渐向低频移动,且第2个和第1个峰值逐渐增大,第3个峰值逐渐减小,在第2个峰值频率(模型潜艇的第2阶整体弯曲模态频率)以上的频段,减小后艉轴承的刚度,对降低整艇结构的振动有利。
4 后艉轴承刚度对潜艇结构水下振动与声辐射的影响
选取后艉轴承和艉轴yz方向刚性连接和yz方向刚度为1.0×106N/m的2种模型进行结构水下振动和声辐射计算。计算时考虑了自由液面的反射作用,艇体中心距水面25 m。图9表示了整艇结构在水中的位置,激振力边界与真空中一致,水下计算频率和步长为:频率范围在10~200 Hz时,步长取2 Hz;频率范围在200~800 Hz时,步长取5 Hz。
采用附加质量附加阻尼算法对SUBOFF潜艇整艇结构水下振动和声辐射特性进行计算,图10为2种工况潜艇整艇结构水下振动与声辐射频响曲线,其中图10(a)为均方法向速度级频响曲线,图10(b)为辐射声功率级频响曲线。由图10可以看出,对于潜艇整艇结构,yz方向刚度为1.0×106N/m相较于yz方向刚性连接,在90 Hz以下结构的振动和辐射声增大,在90~240 Hz结构的振动和辐射声减小,而在240 Hz以上,2条曲线则相互交错。yz方向刚度变小,整艇结构的均方法向速度级频响曲线和辐射声功率级频响曲线的第1个峰值增大,峰值频率不变,第2个峰值增大且峰值频率向低频移动,第3个峰值频率向低频移动,但峰值开始减小,yz方向刚度变小使整艇结构振动的能量和辐射出去的能量都主要向第1个和第2个峰值频率处集中,尤其第2个峰值频率处表现得较为明显,第2个峰值频率成为声能量辐射的主要频率。
图11为SUBOFF潜艇结构振型图,其中图11(a)为工况“yz方向刚性连接”的第1个峰值频率(34 Hz)振型图,图 11(b)为工况“yz方向刚度1.0×106N/m”的第 1个峰值频率(32 Hz)振型图,图11(c)为工况“yz方向刚性连接”的第2个峰值频率(74 Hz)振型图,图11(d)为工况“yz方向刚度1.0×106N/m”的第2个峰值频率(62 Hz)振型图。由图11可以看出,2种工况第1个峰值频率和第2个峰值频率的振型图基本一致。对比模型结构真空中的模态振型可以发现,水下结构的均方法向速度级和辐射声功率级频响曲线的前3个峰值频率正好与其前3阶整体弯曲模态频率一一对应,后艉轴承刚度主要影响模型结构的整体弯曲模态,特别是第2阶整体弯曲模态。
由图11可以看出,在整艇结构振动与声辐射频响曲线的第1个峰值频率处,潜艇整艇结构的振型主要表现为1阶弯曲,潜艇尾部表现为整体振动,后艉轴承刚度对潜艇整艇结构振动与声辐射的影响不大;在第2个峰值频率处,潜艇尾部的整体弯曲开始显现,螺旋桨轴系主要表现为1阶的垂向弯曲模态,降低后艉轴承刚度会使螺旋桨部分振动位移增大,同时传递到艇体结构上的激振力增大,从而导致整艇结构振动增大;在第2个峰值频率以上的频段,降低后艉轴承刚度使经轴系传递到艇体结构上的激振力降低,后艉轴承的隔振作用开始显现。如果把后艉轴承简化为弹簧,艇体简化为质量点,由艉轴承弹簧、艇体质量组成单自由度弹簧质量系统,螺旋桨激振力经后艉轴承弹簧传递到艇体结构上,对艇体结构进行激振。在单自由度弹簧质量系统的固有频率处,弹簧会把激振力放大,而越过这个固有频率,弹簧的隔振效果才会显现;降低弹簧刚度,使单自由度系统的固有频率降低,在固有频率处对激振力的放大效果增强,传递到艇体结构上的激振力增大,使艇体结构振动和声辐射增大;对于固有频率以上的频段,弹簧的隔振效果增强,传递到艇体上的激振力变小,使艇体结构振动和声辐射减小。这也就是降低后艉轴承刚度使整艇结构振动和声辐射频响曲线第2个峰值向低频移动且峰值增大、第2个峰值频率以上的频段振动和辐射声降低的作用机理。
由以上分析可以得出,降低后艉轴承刚度使结构振动与声辐射的能力主要向整艇结构第2阶整体弯曲模态频率处集中,且模型第2阶整体弯曲模态频率向低频移动;在第2阶整体弯曲模态频率以上的频段,降低后艉轴承刚度能够有效降低潜艇整艇结构的振动和声辐射。
以振动均方法向速度和辐射声功率在某频段内的总级作为衡量结构振动大小与声辐射能力强弱的另一标准。在某频段内,如果结构的振动均方法向速度总级大,则相应的结构振动大,反之则结构振动小;而如果结构的辐射声功率总级大,则相应的噪声辐射能力强,反之则噪声辐射能力弱。若工况“yz方向刚性连接”在10~800 Hz频率范围内均方法向速度频响曲线下的面积为,辐射声功率频响曲线下的面积为;工况“yz方向刚度1.0×106N/m”相应频率曲线下的面积分别为,则在10~800 Hz频率范围内,对于振动均方法向速度总级,工况“yz方向刚度1.0×106N/m”比工况“yz方向刚性连接”高出的分贝数为对于辐射声功率总级,工况“yz方向刚度1.0×106N/m”比工况“yz方向刚性连接”高出的分贝数为
分别计算10~80 Hz,80~300 Hz和300~800 Hz这3种频率范围内,对于振动均方法向速度总级和辐射声功率总级,工况“yz方向刚度1.0×106N/m”比工况“yz方向刚性连接”高出的分贝数,如表4所示,负值表示较工况“yz方向刚性连接”低,正值表示较工况“yz方向刚性连接”高。
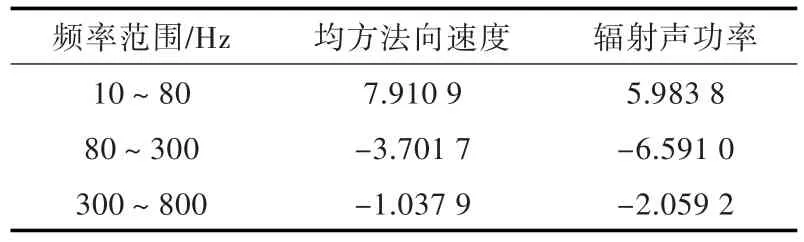
表4 工况“yz方向刚度1.0×106N/m”高出工况“yz方向刚性连接”的分贝数Table 4 The dB number of“1.0×106N/m”being above“rigid connection”
表4进一步验证了降低后艉轴承刚度对潜艇整艇结构振动和声辐射的影响规律,即:后艉轴承刚度降低使结构振动与声辐射的能力主要向其第2阶整体弯曲模态频率处集中,且模型第2阶整体弯曲模态频率向低频移动(在10~80 Hz范围内,降低后艉轴承刚度使潜艇整艇结构的振动和声辐射增大,高出的分贝数均为正值);在第2阶整体弯曲模态频率(工况“yz方向刚性连接”为74 Hz)以上的频段,降低后艉轴承刚度能够有效降低潜艇整艇结构的振动和声辐射(在80 Hz以上频段,高出的分贝数均为负值)。
5 结 论
本文采用SUBOFF艇型,建立了具有螺旋桨结构的潜艇整艇模型,计算了其在垂向力作用下真空中的振动频率特性,并采用附加质量附加阻尼算法计算了其在水下的振动和声辐射特性,对具有不同后艉轴承刚度的潜艇整艇结构振动和声辐射能力进行了对比分析,讨论了后艉轴承刚度对SUBOFF潜艇整艇结构振动和声辐射的影响规律,得到如下结论:
1)降低后艉轴承刚度,使潜艇整艇均方法向速度级和辐射声功率级频响曲线的第2个峰值频率向低频移动,且峰值增大,结构辐射声的能力主要向第2个峰值频率(第2阶整体弯曲模态频率)处集中;
2)在模型第2阶整体弯曲模态频率以上的频段,降低后艉轴承刚度能够有效降低潜艇整艇结构的振动和声辐射。
本文所得结论是针对SUBOFF试验艇得出的,所得结论主要为在声学设计阶段潜艇关键部位结构参数的选取提供参考。
[1]汤智胤,金广文,何琳.潜艇声隐身状态快速评估研究[J].振动与冲击,2008,27(7):113-117.TANG Z Y,JIN G W,HE L.Research on fast evaluation of acoustic stealth condition of submarine[J].Journal of Vibration and Shock,2008,27(7):113-117(in Chinese).
[2]苏强,王桂波,朱鹏飞,等.国外潜艇声隐身前沿技术发展综述[J].舰船科学技术,2014,36(1):1-9.SU Q,WANG G B,ZHU P F,et al.Summarize of foreign submarine acoustic stealth frontier technologies development[J].Ship Science and Technology,2014,36(1):1-9(in Chinese).
[3]KANE J R,MCGOLDRICK R T.Longitudinal vibrations of marine propulsion-shafting systems[J].Transactions of the Society of Naval Architects and Marine Engineers,1949(57):193-252.
[4]LI L W,ZHAO Y,LI T Y,et al.Parameters optimization of the dynamic absorber to control the axial vibration of marine shafting system[J].Journal of Ship Mechanics,2012,16(3):307-319.
[5]周瑞,江祎,管文生.船舶推进轴系纵振计算方法及影响因素分析[J].中国舰船研究,2011,6(6):17-22.ZHOU R,JIANG Y,GUAN W S.Calculation method of ship propulsion shafting longitudinal vibration and influencing factors[J].Chinese Journal of Ship Research,2011,6(6):17-22(in Chinese).
[6]胡芳.推进轴系纵向振动主动控制方法研究[D].上海:上海交通大学,2015.HU F.Research on active control of the longitudinal vibration of propulsion shafting systems[D].Shanghai:Shanghai Jiao Tong University,2015(in Chinese).
[7]杨丽红.螺旋桨纵向力引起的轴系圆柱壳耦合系统振动特性研究[D].哈尔滨:哈尔滨工程大学,2013.YANG L H.Study on vibration of coupled shafting and cylindrical shell caused by propeller longitudinal exciting force[D].Harbin:Harbin Engineering University,2013(in Chinese).
[8]俞强,王磊,刘伟.舰船推进轴系的螺旋桨激励力传递特性[J].中国舰船研究,2015,10(6):81-86,94.YU Q,WANG L,LIU W.Transmission characteristics of propeller excitation for naval marine propulsion shafting[J].Chinese Journal of Ship Research,2015,10(6):81-86,94(in Chinese).
[9]王滨.轴承刚度对船舶轴系振动特性的影响研究[J].齐齐哈尔大学学报,2009,25(6):55-60.WANG B.Effect of bearing stiffness on ship shafting system vibration performance[J].Journal of Qiqihar University,2009,25(6):55-60(in Chinese).
[10]周春良,刘占生,郑洪涛.轴承支承长度及间距对船舶轴系振动特性影响[J].船舶工程,2007,29(5):16-18,55.ZHOU C L,LIU Z S,ZHENG H T.Bearing stiffness to ship shafting system vibration performance[J].Ship Engineering,2007,29(5):16-18,55(in Chinese).
[11]CHERTOCK G.Forces on a submarine hull induced by the propeller[J].Journal of Ship Research,1965,9(2):122-130.
[12]GROVES N C,HUANG T T,CHANG M S.Geometric characteristics of DARPA SUBOFF models[R].Bethesda:David Taylor Research Center,1989.
[13]纪刚,张纬康,周其斗.静水压力作用的水下结构振动及声辐射[J].中国造船,2006,47(3):37-44.JI G,ZHANG W K,ZHOU Q D.Vibration and radiation from underwater structure considering the effect of static water preload[J].Shipbuilding of China,2006,47(3):37-44(in Chinese).
[14]王路才,周其斗,纪刚.肋骨侧向加强对环肋圆柱壳水下振动与声辐射的影响[J].中国舰船研究,2013,8(2):84-89.WANG L C,ZHOU Q D,JI G.Effects of lateral reinforced plates on underwater vibro-acoustic features of ring-stiffened cylindrical shells[J].Chinese Journal of Ship Research,2013,8(2):84-89(in Chinese).
[15]ZHOU Q,JOSEPH P F.A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J].Journal of Sound and Vibration,2005,283(3-5):853-873.
[16]CHEN L H,SCHWEIKERT D G.Sound radiation from an arbitrary body[J].The Journal of the Acoustical Society of America,1963,35(10):1626-1632.
