基于GM（1，N）模型的碳钢腐蚀速率预测

郑如炎，彭飞，牟金磊

1海军驻上海江南造船（集团）有限公司军事代表室，上海201913

2海军工程大学舰船工程系，湖北武汉430033

0 引 言

一般来说，在许多工程应用领域普遍存在金属腐蚀的问题，它涉及面广且危害大，如舰船装备的腐蚀往往会影响舰船的安全航行，抑制舰船战斗力的发挥［1］。在碳钢应用广泛的海洋领域，它具有成本低、工艺性强等优点，约占海洋用金属材料的4/5以上［2］，其腐蚀现象受到普遍关注。因此，研究在海洋环境下影响碳钢腐蚀的主要因素及其腐蚀速率有着非常重要的意义。

为解决碳钢腐蚀速率预测的问题，国内学者邓聚龙教授于1982年提出了灰色理论，研究影响碳钢腐蚀的主要因素，以此达到对碳钢腐蚀速率进行预测的目的。灰色理论主要是基于建模方法对含有部分确知信息、部分不确知信息的灰色系统进行研究，主要解决一些含有未知因素领域的问题，现已广泛应用于地质、农业等学科领域。海洋环境下的腐蚀问题具有高度的复杂性，腐蚀因素部分已知，具体的腐蚀机理未知，这就为灰色理论的应用提供了理论基础。

国内许多学者基于灰色理论也开展了金属腐蚀的预测研究。白真权等［3］基于灰色理论对油气管线腐蚀的剩余寿命进行了预测。喻西崇和谭开忍等［4-5］分别对水管道腐蚀速率以及海底管道腐蚀寿命进行了灰色预测。王海涛等［6］基于GM（1，1）模型对碳钢的腐蚀速率进行了研究，探讨了影响海水腐蚀的主要因素。任竞争等［7］建立了GM（1，N）模型对钢材腐蚀速率进行了预测。刘海霞等［8］运用灰色理论针对大气腐蚀情况下金属材料的使用寿命进行了预测。

总体上，国内学者对于碳钢等船用金属腐蚀速率的灰色理论应用研究主要局限于GM（1，1）模型，少部分采用GM（1，N）模型。对于GM（1，1）模型，根据灰色理论的“新信息优先”理论，新信息的作用或价值大于老信息，即赋予多方面的新信息较大权重可有效提高所建模型的效能［9］，但GM（1，1）模型的精度有待提高；而对于现有的GM（1，N）模型，虽然精度有所提高，但仍存在限制条件多的问题。

本文将主要以碳钢腐蚀速率为应变量，腐蚀因素为自变量进行灰关联分析，以得到影响腐蚀速率的关键因素。在此基础上建立最优GM（1，N）灰色模型，以对碳钢腐蚀速率进行预测，进而为船用金属腐蚀寿命的研究提供理论支撑。

1 碳钢腐蚀速率和环境因素的灰关联分析

1.1 灰关联分析方法的步骤

灰关联分析方法［9］是依据各因素间的相异或相似度（亦称“灰关联度”）作为衡量各影响因素间关联度的一种方法，其主要步骤如下：

1）对海洋环境因素和碳钢腐蚀数据进行无量纲处理。本文采用常用的均值化处理方法，如式（1）所示。

式中：Yi为因素均值数列，i=0时为母因素的均值数列，i=1,2,…,N时为子因素的均值数列；为因素序列，i=0时为母因素序列，i=1,2,…,N时为子因素序列。其中,i为因素排列位置，N为子因素个数，k为某因素排列位置对应的变量序列号，m为各因素中包含的序列个数。

2）计算灰关联系数ξi。

灰关联系数可由式（2）计算得到：

式中：ξi(k)为灰色理论定义的灰关联系数；α为分辨系数，取值在0～1之间，绝大多数取为0.5；Y0(k)为母因素均值数列；Yi(k)为子因素均值数列，i≠0。

3）计算灰关联度。

灰关联度可由式（3）计算得到：

式中，γi为灰关联度，由其构成的序列γ1,γ2,γ3,…,γN描述各子因素对结果的影响情况，其中γi越大，影响程度就越大。

1.2 碳钢腐蚀与海洋环境因素的灰关联分析

关于我国4个海域海洋环境因素及Q235碳钢在上述海域1年内的腐蚀数据［10］如表1所示。

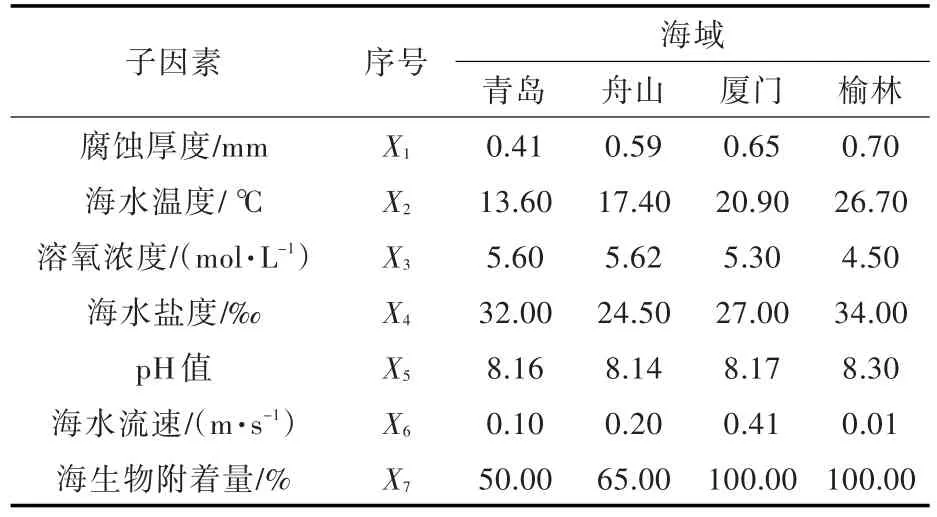
表1 海洋环境因素及腐蚀数据Table 1 Sea environmental factors and corrosion data

2 GM（1，N）腐蚀速率预测模型

GM（1，N）是多维灰色模型的符号，其中“1”指一阶，“N”指变量（子因素）个数，变量又包含1个自变量和N-1个因变量。建模的具体步骤如下［11］：

1）建立初始序列。

2）初始序列集的一阶累加生成。

式中，t和l为变量序列号。

3）建立微分方程。

式中：a为系统发展系数；为系统驱动项，其中bi为系统驱动系数；为第1个变量的初始k序列；为相邻累加生成序列和的均值。

4）求解灰参数。

式中，b2,b3,…,bN与式（6）同理，为系统驱动系数；B，YN为系统参数包PN的矩阵因子。由此可根据基于微分方程的最小二乘法求解灰参数，即

5）还原间隔方程。

通过式（8）求得的灰参数还原间隔方程［13］为

3 GM（1，N）模型实例验证

3.1 腐蚀速率预测模型

关于腐蚀速率的预测模型［13-14］一直是防腐领域的研究热点问题。本文主要参考表1提供的数据和灰色理论，选择碳钢在相关海域1年内的平均腐蚀速率为自变量，海水温度、海生物附着量、pH值和海水盐度等为因变量，构成初始序列如下：

根据最小二乘法可求得PN为

碳钢腐蚀速率预测方程为

关于舟山、厦门和榆林海域海洋环境下影响腐蚀速率的实测值、预测值、相对误差结果，如表2所示。由表可知，改进型GM（1，5）模型得到的预测值与实测值非常接近，平均相对误差约为6.77%。

3.2 GM（1，N）模型优选

1）不同维数模型优选。

为验证GM（1，5）模型是否为最优GM模型，建立了4，6和7维的GM模型与GM（1，5）模型进行对比，其中GM模型仍按因素的影响程度排列。具体初始序列如下：

采用不同维数的GM模型对碳钢在不同海域海洋环境下的腐蚀速率进行预测，预测结果与在上述海域的实测值进行了对比，如表3和图1所示。由此可知，GM（1，5）模型精度最高。

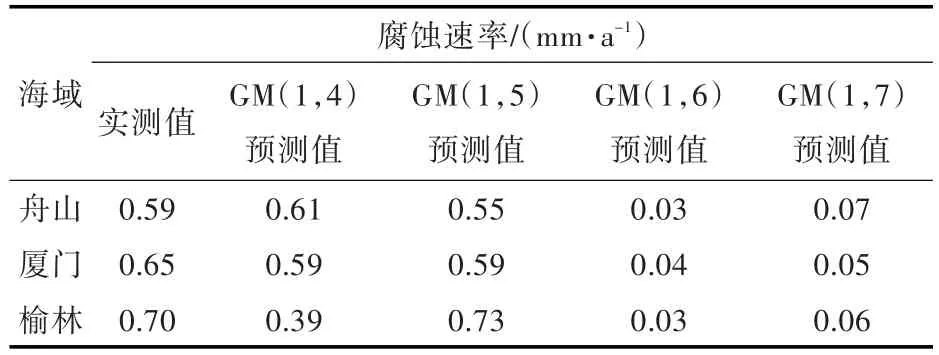
表3 不同维数的GM模型预测值和实测值对比Table 3 Comparison of prediction data and measuredresults based on different dimensions'GM model

2）基于变量顺序的GM（1，5）模型优选。

为验证GM（1，5）模型的变量顺序是否影响模型精度，另外建立了2种GM（1，5）模型进行对比分析，具体初始序列如下：

按照不同变量顺序，运用GM（1，5）模型对碳钢在舟山、厦门和榆林海域海洋环境下的腐蚀速率进行预测，其结果与在上述海域的相应实测结果进行对比，如表4和图2所示。由此可知，GM（1，5）模型中按照影响因素的影响程度排列的模型精度最高。

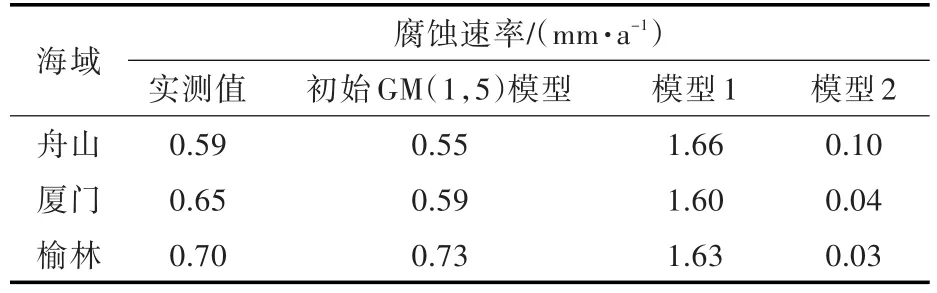
表4 不同变量顺序的GM模型预测值和实测值对比Table 4 Comparison of prediction data and measured results based on the different sequence of variables'GM model

由上述结果可知，本文所建GM（1，5）模型在确保精度的同时还减少了计算量，为所建GM模型中的最优模型。

3.3 两种预测方法的结果比较

文献［15］给出了一种基于回归分析的古柏近似函数模型（以下称Cooper模型）求解腐蚀速率的方法，具体表达式为

式中：dm为规定腐蚀厚度；p为最大腐蚀厚度小于或等于dm的概率；x为最大腐蚀厚度的随机变量；xˉ为平均腐蚀厚度；xm为最大概率密度的腐蚀厚度。

表5所示为厦门和榆林海域采用Cooper模型的预测值与实测值之间的误差分析结果。结合表2得到腐蚀速率随不同海域变化的柱状图（图3）。从表2，表5和图3可以看出，腐蚀实测值在GM模型应用中，最大相对误差为9.23%，平均相对误差为6.77%；应用Cooper模型预测的结果最大相对误差为21.54%，平均相对误差为21.49%。通过与Cooper模型预测结果的比较，基于GM（1，N）模型对碳钢腐蚀速率的预测能够得到误差较小的结果，且预测精度较高。

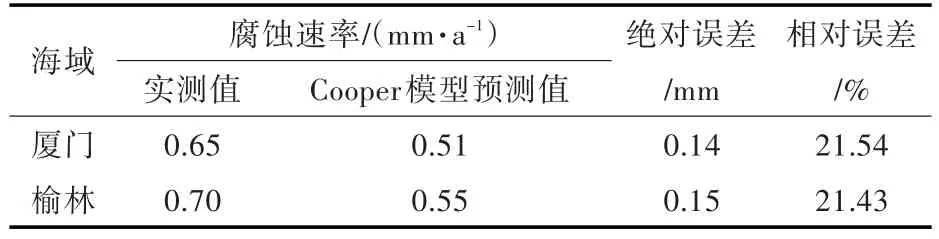
表5 Cooper模型预测值与实测值的精度误差分析Table 5 Precision and error analysis between Cooper model and measured results

4 结 论

为了研究碳钢在海洋环境下影响腐蚀速率的因素，本文以碳钢腐蚀速率为应变量、腐蚀因素为自变量进行了灰关联分析，得到影响腐蚀速率的关键因素。在此基础上，建立了GM（1，N）灰色模型，并对碳钢在不同海域下的腐蚀速率进行了预测，得到如下结论：

1）在我国青岛、舟山、厦门、榆林海域海洋环境下影响碳钢腐蚀速率的主要因素是海水温度、海生物附着量、pH值和海水盐度。

2）基于灰色理论建立的GM（1，5）模型可有效预测碳钢腐蚀速率，且具有较高精度；通过该模型对舟山、厦门、榆林海域海洋环境下腐蚀速率的预测结果与实测值的对比发现，平均相对误差仅为6.77%；相较于其他多维数以及不同变量顺序的模型，GM（1，N）模型也最优，与Cooper模型相比，精度更高。

3）建立的GM（1，N）模型可有效预测碳钢腐蚀速率，同时可为腐蚀剩余寿命预测方法的研究提供参考，具有一定的应用价值。

4）鉴于建立的多种对比模型计算量较大，可考虑用Matlab编写GM（1，N）模型通用程序，进而可极大地减少计算量，但对于该模型能否适用于多年海洋环境下碳钢的腐蚀速率预测仍需进一步验证。

本文仅考虑了几种海洋环境下的影响因素，下一步有必要对包括海生物附着的种类等更大的可能影响因素和温度数据的有效性进行研究。

［1］牟子方，魏汝祥.基于维修规划的舰船船体腐蚀防护经济性分析［J］.中国舰船研究，2016，11（3）：122-127.MU Z F，WEI R X.Cost effectiveness assessment of ship hull corrosion protection based on the maintenance plan［J］.Chinese Journal ofShip Research，2016，11（3）：122-127（in Chinese）.

［2］夏兰廷，黄桂桥，丁路平.碳钢及低合金钢的海水腐蚀性能［J］.铸造设备研究，2002（4）：14-17.XIA L T，HUANG G Q，DING L P.Sea water corrosion properties of carbon steel and low alloy steel［J］.Research Studies on Foundry Equipment，2002（4）：14-17（in Chinese）.

［3］白真权，路民旭，赵新伟.油气管线腐蚀剩余寿命预测研究现状分析［J］.天然气与石油，1998，16（1）：31-34.BAI Z Q，LU M Q，ZHAO X W.Study on corrosion remaining life of oil&gas pipeline［J］.Natural Gas and Oil，1998，16（1）：31-34（in Chinese）.

［4］喻西崇，赵金洲，邬亚玲，等.利用灰色理论预测注水管道腐蚀速率的变化趋势［J］.腐蚀与防护，2003，24（2）：51-54，69.YU X C，ZHAO J Z，WU Y L，et al.Using gray model to predict corrosion rate variation with time in injecting pipeline［J］.Corrosion and Protection，2003，24（2）：51-54，69（in Chinese）.

［5］谭开忍，肖熙.基于灰色理论的海底管道腐蚀剩余寿命预测方法［J］.上海交通大学学报，2007，41（2）：186-188，193.TAN K R，XIAO X.The forecast of remaining life of corrosive submarine pipelines based on grey theory［J］.Journal of Shanghai Jiaotong University，2007，41（2）：186-188，193（in Chinese）.

［6］王海涛，韩恩厚，柯伟.灰色理论对碳钢、低合金钢海水腐蚀的预测和分析［J］.腐蚀与防护，2005，26（9）：373-374.WANG H T，HAN E H，KE W.Prediction and analysis of seawater corrosion of carbon steel and low alloy steels by gray theory［J］.Corrosion and Protection，2005，26（9）：373-374（in Chinese）.

［7］任竞争，谭世语，周志明，等.GM（1，N）模型进行钢材腐蚀速度预测及腐蚀因素敏感性分析［J］.材料保护，2010，43（8）：21-24.REN J Z，TAN S Y，ZHOU Z M，et al.Prediction of corrosion rates and sensitivity analysis of corrosion factors of steels based on GM（1，N）model［J］.Materials Protection，2010，43（8）：21-24（in Chinese）.

［8］刘海霞，程学群，李晓刚，等.A1060纯Al的海洋大气环境腐蚀寿命预测模型研究［J］.中国腐蚀与防护学报，2016，36（4）：349-356.LIU H X，CHENG X Q，LI X G，et al.Corrosion prediction model of Aluminum 1060 in marine atmospheric environment［J］.Journal of Chinese Society for Corrosion and Protection，2016，36（4）：349-356（in Chinese）.

［9］刘思峰，郭天榜，党耀国.灰色系统理论及其应用［M］.北京：科学出版社，2015.

［10］黄桂桥.碳钢在我国不同海域的海水腐蚀行为［J］.腐蚀科学与防护技术，2001，13（2）：81-84，88.HUANG G Q.Corrosion behavior of carbon steels immersed in sea areas of China［J］.Corrosion Science and Protection Technology，2001，13（2）：81-84，88（in Chinese）.

［11］晋小莉，解志坚，李宗虎，等.转管武器射速研究的GM（1，N）模型方法［J］.火炮发射与控制学报，2006（3）：1-5.JIN X L，XIE Z J，LI Z H，et al.Model GM（1，N）method study about rate of fire of gatling gun［J］.Journal of Gun Launch&Control，2006（3）：1-5（in Chinese）.

［12］邓聚龙.灰预测与灰决策［M］.武汉：华中科技大学出版社，2002.

［13］IVANOV L D，SPENCER J，WANG G.Probabilistic evaluation of hull structure renewals for aging ships［C］//Proceedings of the 8th International Marine Design Conference（IMDC）.Athens，Greece：IMDC，2003.

［14］MELCHERS R E.The changing character of long term marine corrosion of mild steel［J］.Centre for Infrastructure Performance and Reliability，2010，30（6）：770.

［15］曹楚南.腐蚀试验数据的统计分析［M］.北京：化学工业出版社，1988.