基于M估计的转子不平衡量的识别

魏巍，张海鹏，谈演

摘 要：转子不平衡问题是旋转机械故障中经常发生的问题，因此对不平衡量大小相位的识别至关重要。利用传统的最小二乘法计算的转子不平衡量受异常值影响较大。加权最小二乘法需要对振动数据的处理较为繁琐并且权重大小难以确定。现提出一种基于M估计的转子不平衡量的识别方法，该方法具有稳健性，受异常值的影响较小，且便于计算权重。通过实验证明，该方法可以得到转子的不平衡量。

关键词：动平衡；影响系数法；最小二乘法；M估计

中图分类号：V231.9 文献标志码：A 文章编号：2095-2945（2018）06-0087-03

Abstract： Rotor unbalance is a common problem in rotating machinery fault， so it is very important to identify the phase of unbalance. The rotor unbalance calculated by the traditional least square method is greatly affected by the outliers. The weighted least square method needs to deal with the vibration data more cumbersome and the weight is difficult to determine. In this paper， a method of rotor unbalance recognition based on M estimation is proposed. This method is robust， less affected by outliers， and easy to calculate weights. It is proved by experiments that the unbalance of rotor can be obtained by this method.

Keywords： dynamic balance influence coefficient method； least square estimation； M estimation

引言

转子的不平衡量对转转子影响非常大，过大的不平衡量会直接损坏机器，所以对转子不平衡量的准确识别具有很大的意义。传统的影响系数法可以简单方便识别，但存在病态方程。最小二乘法和影响系数法的结合能够解决病态方程，但不具有稳健性；加权最小二乘法需要对转子的振动数据进行深入分析。本文通过M估计对转子的不平衡量进行识别，具有较好的稳健性，通过实验证明，M估计可以有效识别转子的不平衡量。

1 转子回归模型

影响系数法是转子动平衡最常用的方法。但是影响系数法存在病态方程，所以现经常采用影响系数法和最小二乘法相结合。影响系数矩阵可采用有限元模型或历史平衡记录获得。根据线性振动理论，在m个转速，n个测振点，q个平衡平面下，转子平衡方程为：

[L]=[L0]+[A]×[W]（1）

其中，[L]为各测点的残余振动；[L0]为转子在不平衡量下引起的各测点的初始振动；[A]为影响系数；[W]为校正质量。

矩阵形式表达为：

[L]、[L0]为p=m×n的列阵，[W]为q个平衡质量列阵。{A}是影响系数p×q的矩阵。当P=q时，方程有唯一解，而在实际平衡过程中经常出现P>q的情况，此时，需要对方程采用最小二乘法的原理，即最小化残差平方和，用矩阵形式表示有：

[W]=-（[A]T[A]）-1[A]T[L]

式（2）又可以转化为多元回归问题：

li=l0i+ai1·w1+ai2·w2+…+aiq·wq（i=1，2，3，…，p）（3）

2 M估计

稳健估计基本可以分为三大类型：M估计、L估计、R估计。其中M估计（Maximum Likelihood Type Estimates）是经典极大似然估计的推广，称为广义极大似然估计，本文主要讨论M估计。

设观测样本L1L2…Ln，X为待估参数，观测值的分布密度为f（li，■），极大似然估计准则为

■lnf（li，■）=max

用ρ（*）代替-lnf（*），则极大似然估计准则可以改为

■ρ（li，■）=min

对上式求导，得：

■φ（li，■）=0

其中：φ（li，■）=■

由以上可知，有一个ρ函数，就定义了一个M估计。

几种常见的ρ函数

（1）huber函数

通常情况下k=1.345，既能保證稳健性，又具有较高的估计效率。

（2）tukey函数

通常k=4.685，估计方法既稳健又有较高的估计效率。

（3）Hampel函数

通常取a=1.5，b=3，c=8，Hampel函数更为复杂一些，但当|u|>c时权因子取到了0，因此它具有更好的稳健性。

其中u=■

■为尺度参数，取绝对离差中位数：■=median（|v-median（v）|）

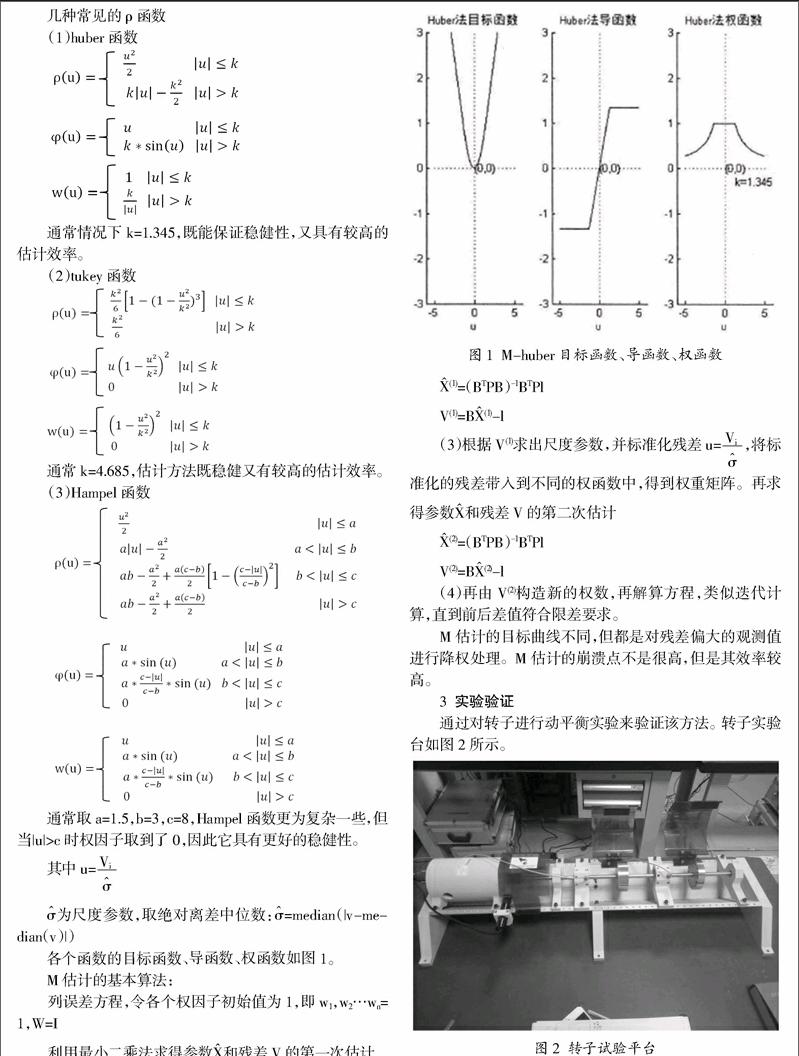
各个函数的目标函数、导函数、权函数如图1。

M估计的基本算法：

列误差方程，令各个权因子初始值为1，即w1，w2…wn=1，W=I

利用最小二乘法求得参数■和残差V的第一次估计

■（1）=（BTPB）-1BTPl

V（1）=B■（1）-l

（3）根據V（1）求出尺度参数，并标准化残差u=■，将标准化的残差带入到不同的权函数中，得到权重矩阵。再求得参数■和残差V的第二次估计

■（2）=（BTPB）-1BTPl

V（2）=B■（2）-l

（4）再由V（2）构造新的权数，再解算方程，类似迭代计算，直到前后差值符合限差要求。

M估计的目标曲线不同，但都是对残差偏大的观测值进行降权处理。M估计的崩溃点不是很高，但是其效率较高。

3 实验验证

通过对转子进行动平衡实验来验证该方法。转子实验台如图2所示。

转子影响系数矩阵通过多次实验得到。在确定转子无故障前提下，在平衡面A处0°位置添加已知不平衡量0.8g，测量转子在此不平衡下两个测点的振动信息如图3所示。

现已知不平衡质量，对计算效率和稳健性等因素综合考虑，采用M-huber。用最小二乘法和M-huber估计计算转子不平衡量的大小和相位，结果如表1所示。采用不平衡量实际值w和估计值■的相对误差比较两种方法的效果，相对误差为

M-huber估计在各个转速下的权重如图4所示

通过以上结果可知，利用M-Huber估计可以更好的识别转子的不平衡量，相对误差大大减少。根据M-huber估计得到的权重在转子一阶临界转速下减小，与转子一阶临界转速下转子振动数据存在异常值一致。

4 结束语

在综合考虑计算效率和稳健性等因素，采用M-huber估计。通过M估计得到的不平衡质量与传统的最小二乘法影响系数法相比较，具有更高的精确度，相对误差大大降低。应用M估计识别转子不平衡量，降低了转子一阶临界转速附近的权重，与转子一阶临界转子下振动数据存在异常一致。

参考文献：

[1]缪海林.基于模型的转子系统不平衡量识别的鲁棒方法研究[D].南京航空航天大学，2012.

[2]王海娜.线性回归模型的若干稳健估计方法及应用实例[D].山东大学，2013.

[3]Pennacchi P，Chatterton S，Ricci R.Rotor balancing using high breakdown-point and bounded-influence estimators[J].Mechanical Systems and Signal Processing，2010，24（3）：860-872.

[4]杨庆华.用最小二乘法影响系数法对高速柔性转子的动平衡研究[J].机电工程，1998.

[5]Pennacch P，Vania A，Bachschmid N.Increasing the robustness of fault identification in rotor dynamics by means of m-estimators[J].Mechanical Systems and Signal Processing.2007，21（8）：3003-3029.