调节阀空化噪声数值分析

陈修高，张希恒，王世鹏，王 雁

（兰州理工大学 石油化工学院，兰州 730050）

随着社会工业的发展，调节阀被广泛应用于国民经济的各个领域，其主要作用是控制管路中介质的流向、流量、压力等，工业控制阀的应用趋向于成套化、大型化、标准化，但是调节阀中极易出现的空化问题成为影响其发展的重要因素。空化的产生通常会造成阀体的剥蚀、振动、噪声，严重时导致阀门失效，缩短使用寿命。

目前利用空化噪声信号进行空化状态程度识别已经成为空化检测的重要方法[1]，研究者们已经对离心泵、螺旋桨、水翼等进行了空化噪声研究工作[2-5]。而使用数值分析方法研究阀门空化噪声的却很少，陆亮[6]用理论和实验的方法对节流阀空化流动及其噪声进行了研究；杨国来等[7]利用CFD（Computational Fluid Dynamics）研究了调节阀内的空化位置，使用理论计算的方法研究了空化噪声的影响因素。随着计算机数值仿真技术的发展，新的联合仿真技术成为研究空化噪声的有效方法[2-3,8]，联合仿真技术是将两个及以上软件有机地结合起来，利用各个软件的优点对实际工程问题进行数值分析，具有成本低、周期短，准确性高的优点，同时可以获得更多的数据资源。

本文利用CFD和LMS Virtual lab联合仿真方法研究调节阀空化程度不同时的声场特征并建立两者的关系，目的是为通过声学信号定量检测调节阀空化程度提供帮助，同时也为工业阀门空化噪声问题的研究提供一种新方法，对于工程应用具有重要意义。

1 流场计算

1.1 几何模型

本文以一种轴流式调节阀为分析对象，研究由于阀内空化现象而产生的噪声问题。使用Solidworks2016建立调节阀的三维模型，并对模型进行适当的简化处理，为了使阀内流体流动充分均匀以及噪声振动数值计算接近实际工况，对阀门进出口两端加长管道。然后使用ANSYS Workbench提供的DM（Design Modeler）模块反向建模，抽取内部流道区域，调节阀结构与内部流道区域如图1所示。

图1 调节阀结构与内部流道

利用ANSYS ICEM CFD对流体区域划分网格，网格采用混合网格划分技术，为了使计算结果准确，对阀门内部网格进行局部加密处理，网格划分结果如图2所示。

图2 流体区域网格划分

在数值模拟当中网格的数量会直接决定计算结果的准确性，计算之前需对网格密度进行无关性检验，无关性检验如表1所示。

表1 网格无关性检验

划分5种不同数量的网格方案，比较阀门出口的平均质量流量，当网格数量增加至5.79×105以上后，阀门出口的平均质量流量基本保持稳定，网格数量为2.98×105时计算结果相对误差较大，考虑计算时间，选择网格数量为5.79×105较为合理。

1.2 计算方法

声振耦合声学响应计算需要CFD流场信息作为激励信号，利用CFD软件Fluent对调节阀内部空化流场进行稳态和瞬态计算。

首先需要进行稳态计算，采用有限体积法，使用Pressure-Based求解器求解，选择Steady稳态类型，使用Mixture混合模型和RNGk-ε湍流模型[9]，近壁面处理采用标准壁面函数（Standard Wall Functions）法[10]。压力项、密度、动量、湍动能的离散采用2阶迎风格式，边界条件如表2所示，待稳态计算收敛后，进行瞬态计算。

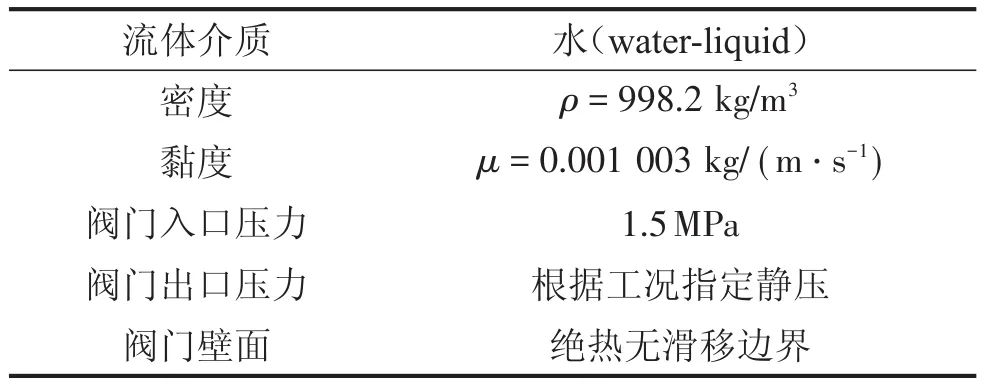
表2 边界条件设置

瞬态计算以稳态计算结果为初值，使用LES大涡模拟，进行瞬态流场计算，将瞬态流场的计算信息作为声场计算的激励信号。在瞬态计算中，时间步长设置为5×10-5s，采样频率为20 kHz，根据采样定律，最大分析频率可达到10 kHz。

LES大涡模拟能够描述小尺度湍流流动，但是计算量远小于DNS直接数值模拟[11-12]。其控制方程如下，经空间滤波运算的滤波操作后，Navier-Stokes方程表达式为

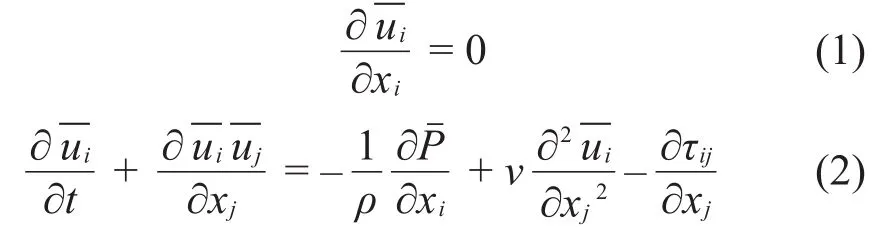
式中：i,j=1,2,3；ui表示与xi相关联的速度分量，表示经过滤波后的平均速度分量；ν为流体的运动黏性系数，ρ为流体的密度；τij是亚格子应力，代表了小尺度运动对大尺度运动的影响

根据Boussinesq假设，亚格子应力张量表达式为

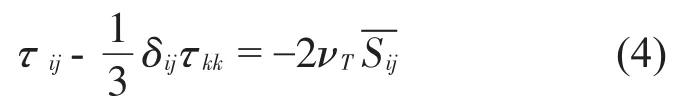
其中：νT是亚格子涡黏性系数，为涡团速度尺度和长度尺度的函数；为雷诺尺度应变张量

将式(4)和式(5)代入式(2)中可得

方程式（6）即为LES大涡模拟的控制方程。

1.3 空化模型与空化数

通过对Zwart-Gerber-Belamri模型、Kunz模型和Schnerr-Sauer模型3种空化模型进行对比分析，得出Zwart-Gerber-Belamri空化模型更能体现出空化核数量对空化行为的影响[9]，计算结果更加接近于实际值[2,13-14]，所以采用Zwart-Gerber-Belamri空化模型。其控制方程如下：

当Pv≥P时

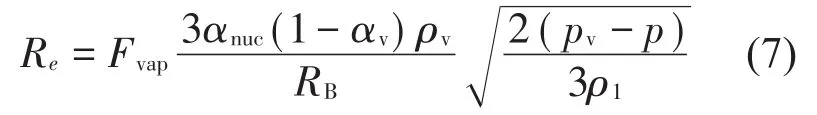
当Pv＜P时

式中：Pv为饱和蒸汽压，αnuc为空化汽相成核处体积分数，αv为蒸汽相体积分数，RB为空泡半径，Re为蒸发相生成率，Rc为凝结相生成率，Fvap为汽化校正系数，Fcond为凝结校正系数。

空化数为描述空化程度的无量纲参数，由阻止液流空化的力与促进液空化的力之比计算得到，空化数越小，空化程度越强。空化数定义式如下

式中：p0为基准点压力，u0为基准点速度，pv为液体饱和蒸气压。

2 声场计算

2.1 Lighthill声类比理论

声场计算需要通过Lighthill声类比理论方程提取声源项，由流体力学中的N-S方程推导得到了Lighthill声类比理论方程：

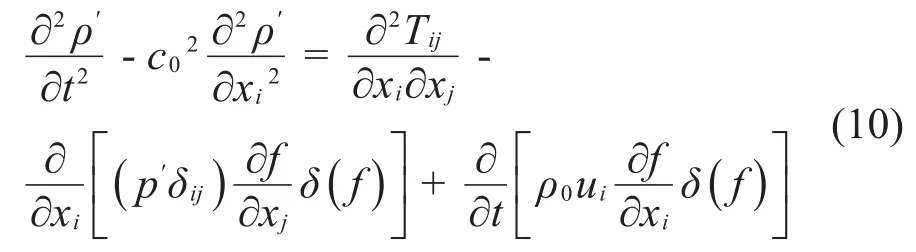
式中，T为Lighthill应力张量，δij为Kronecker函数，c0为等熵条件下的声速，ρ'=ρ+ρ0，ρ和ρ0分别是受扰动时和未受到扰动时的流体密度，ui为流体速度，p'为流体所受到的压强变化量，f为边界控制函数。

2.2 计算方法

将通过Fluent瞬态计算得到的脉动信息CGNS文件作为激励信息导入到LMS Virtual Lab进行声振耦合和辐射声场计算。

声场计算的结构网格、声学网格和场点网格划分如图3所示。结构与声学网格为四面体类型，声学网格即为结构网格的外壁面。在划分声学网格时，网格大小要一致，不能出现过大或者过小的情况，局部网格划分过小也并不能提高计算精度，还会增加计算时间[15]。设置场点网格目的是计算外部辐射声场，网格类型为正方形。

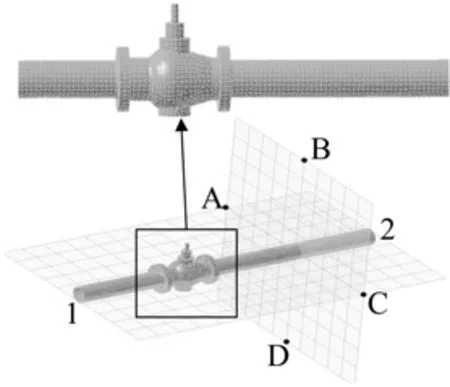
图3 声学网格与场点网格

根据最新标准《IEC 60534-8-2-2015工业过程控制阀第8-2部分噪声的考虑：通过控制阀的流体产生的噪声的实验室测量》的规定，噪声监测点应距离阀出口处大于等于1 m，且距离管道壁面为1 m。设置四个监测点A、B、C、D，如图3所示，与阀门出口距离为1 m，且与管道壁面距离为1 m。

2.3 边界条件及参数设置

根据调节阀的实际使用工况，需要对调节阀的管路系统添加约束，进口管段1固定，出口管段2简支，如图3所示。

设置结构材料属性：杨氏模量为1.75×1011N﹒m-2，泊松比为0.3，密度为7 800 kg/m3。外部辐射声场流体域为空气，所以设置声学网格的流体材料为空气，属性定义密度为1.225 kg/m3，声速为340 m/s。

将流场激励信息通过快速傅里叶变换（FFT，Fast Fourier Transformation）转移至结构网格上，同时对时域数据进行FFT转化到频域，最后进行声振耦合响应计算，得到外部声场分布特征以及声压级频率响应函数。

2.4 理论预测方法

根据最新标准《IEC60534-8-4-2015工业过程控制阀第8-4部分噪声的考虑：液体动力流产生噪声的预测》中关于调节阀内有空化流的噪声计算公式，对距离阀门出口为1 m且距离管道壁面为1 m处的位置，进行理论预测计算。计算方法如下[16]：

空化流状态下频率为fi的内部声压级

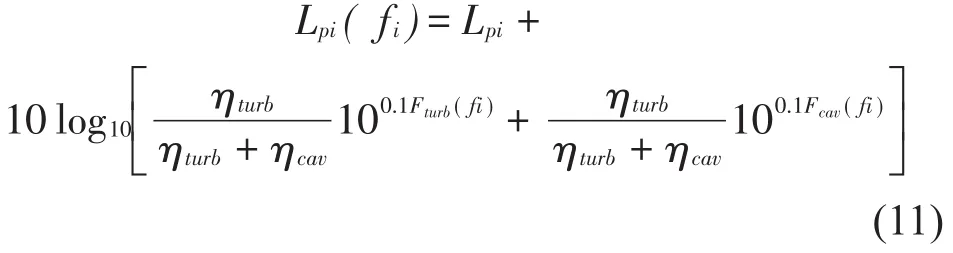
频率为fi时的传播损失

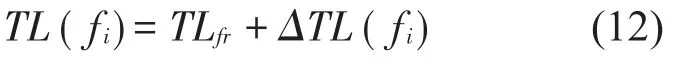
频率为fi时外部1 m处的声压级

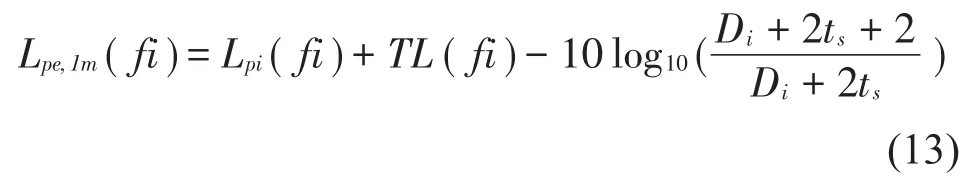
外部1 m处总声压级为

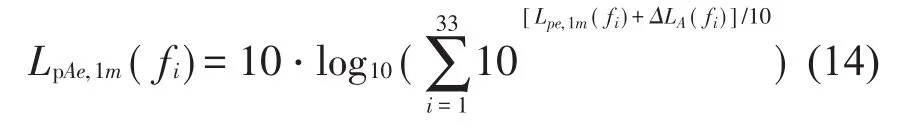
式中：Lpi(fi)为fi频率下的内部声压级，Lpi为内部声压级，ηturb和ηcav分别是湍流和空化流状态下的声效系数，Fturb(fi)和Fcav(fi)分别为湍流和空化流状态下频率分布函数，TLfr为环形频率最小传播损失，ΔTL(fi)为修正fi的传播损失，Di和ts分别为下游管道内径和管道壁厚，ΔLA(fi)为“A”权重因子。

3 计算结果与分析

3.1 阀门开度对空化噪声的影响

采用调节阀比较容易实现空化以及常用的20%、30%、40%和50%4个相对开度，出口压力统一设为0.55 MPa，对其进行声振耦合数值分析。

图4是出口压力在0.55 MPa时4个相对开度下节流截面处空化区域图。由图4可得，开度不同，阀芯移动造成流通截面积不同，使得各开度下的空化程度不同，随着开度的增大，空化程度呈先减小、后增加的趋势。

图5为50%开度时设置的四个监测点处的总声压级与理论计算得到的总声压级对比曲线图，从图5中可以得到，监测点处总体声压级基本一致，符合噪声传播的实际分布规律，同时理论计算得到的结果与数值计算结果相对误差在6%以内，证明了数值计算的准确可行性。

图6是各开度下在监测点A的声压级频率响应曲线，从图6中可以看出，各开度下的数值计算结果整体趋势基本一致但具体数值不同，说明同一阀门空化噪声的特征基本相似，但具体总噪声级不同。声压级在低频160 Hz和260 Hz时具有两个明显的峰值点，在中频820 Hz和1 700 Hz处有两个峰值点，这些峰值点是调节阀空化噪声的主要组成部分。

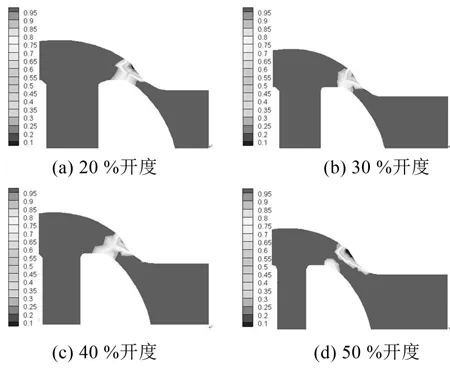
图4 出口压力为0.55 MPa时各开度下节流处空化区域图

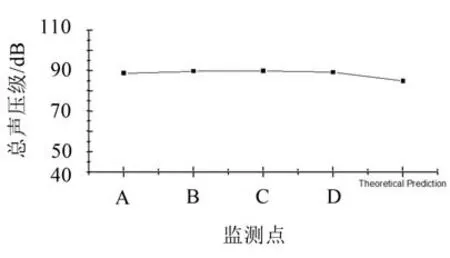
图5 监测点处和理论预测的总声压级

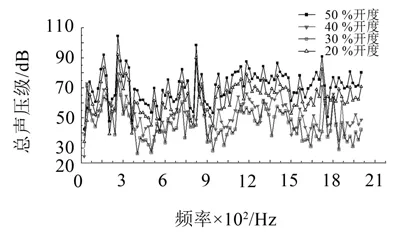
图6 各开度下监测点A处声压级频率响应曲线

图7是调节阀管阀系统4个开度下在频率为160 Hz时的声压级分布云图，从图7中可得，由于阀门节流处有空化现象，所以声压级峰值也主要集中分布在阀门此处的阀体外部，声压级是沿调节阀管阀系统呈现对称分布的，此现象符合噪声辐射实际分布规律。

图8为通过B-spline插值法拟合得到的各开度下监测点A的总声压级变化趋势图，总声压级随着开度的增加同样呈现出先减小后增大的趋势，与文献[17]中的规律相似。由于小开度下流通面积较小，节流程度很大，导致压降很大，空化程度较强，噪声强度较大；随着开度增大，流通面积增大，节流程度减小，空化程度减小，噪声强度减小；但当开度继续增大时，流量增大，流速增加，空化程度增大，噪声强度也随之增大。

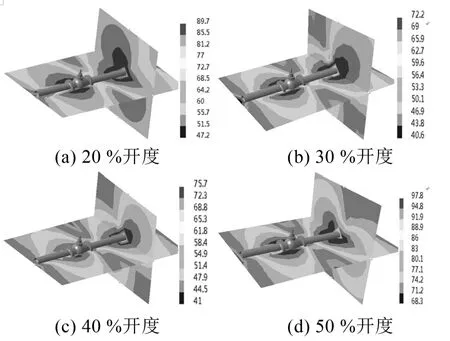
图7 各开度下频率为160 Hz时的声压级分布云图

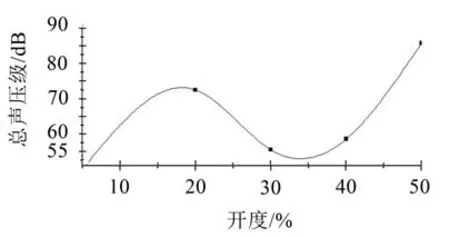
图8 各开度下监测点A的总声压级变化曲线

通过计算空化数来表征空化程度的强弱，计算结果如表3所示，表3即为阀门各开度下监测点A处空化强度与总声压级的对应关系。

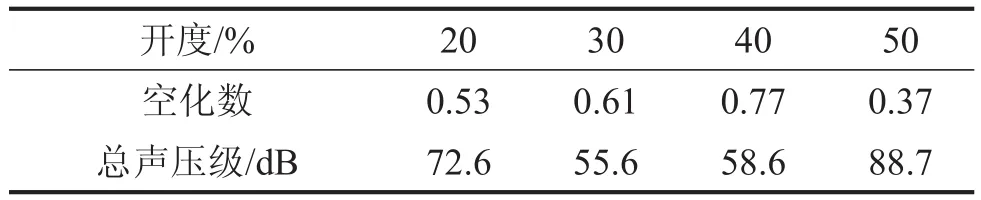
表3 各开度下监测点A处空化强度与总声压级关系

3.2 压差对空化噪声的影响

固定调节阀为50%开度，分别对出口压力为0.45 MPa、0.55 MPa、0.75 MPa和0.95 MPa时的工况进行数值分析。

图9是阀门50%开度时，不同出口压力下节流截面处空化区域图。由图可9得，出口压力越小，压差越大时，空化区域越大、程度越强；反之，则越小越弱。在出口压力为0.45 MPa时，气泡的产生已经非常强烈，气泡开始阻塞流道，严重时会使阀门失去调节作用。

图10为阀门在50%的相同开度下不同压差时监测点A的声压级响应曲线，从图10中可以明显看出，在相同开度时，不同压差时的声压级频率响应曲线趋势基本一致，但在具体数值上明显不同。图11为在峰值点频率260 Hz下的声压级分布云图，声压级辐射沿调节阀管阀系统呈现对称分布的规律，最大噪声基本出现在空化区域的阀体外部附近。

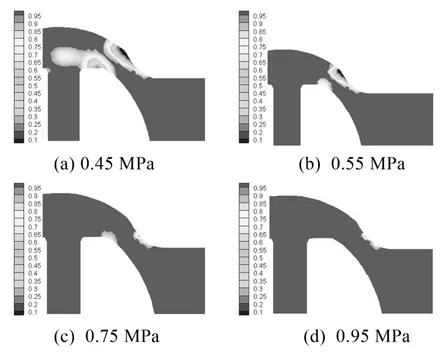
图9 开度为50%时不同出口压力下节流处空化区域图

图10 不同出口压力下监测点A处声压级频率响应曲线

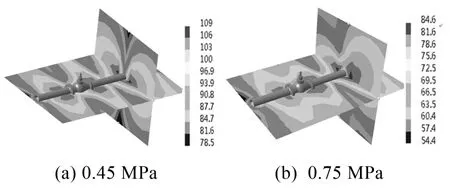
图11 不同出口压力下频率为260 Hz时的声压级分布云图

图12是不同压差下监测点A的总声压级变化曲线，由图可以得到，不同出口压力下总声压级明显不同，在空化程度越强的压差下，产生的噪声也越大，且可以明显区分；在空化程度较弱的压差下，噪声也很小，由于出口压力0.75 MPa和0.95 MPa的空化程度相差不大，所产生的噪声级也相差很小。

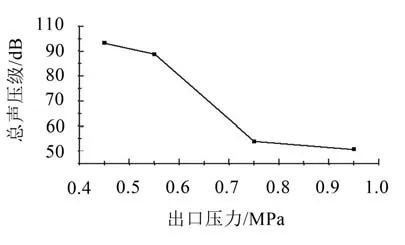
图12 不同出口压力下监测点A的总声压级变化曲线

计算各压差下的空化数来表征其空化程度的强弱，表4所示为阀门各开度下监测点A处空化强度与总声压级的对应关系。

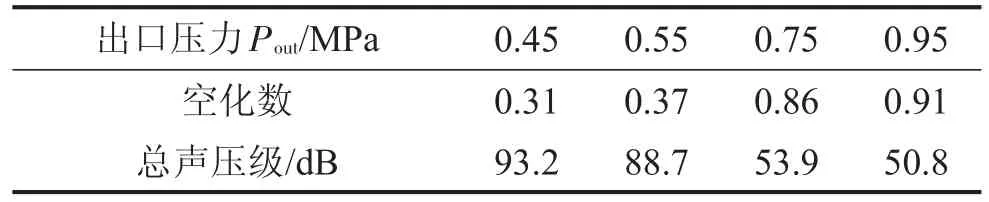
表4 不同出口压力下监测点A处空化强度与总声压级关系

可以使用数值分析技术来为声学检测提供数据支持，建立空化程度与噪声的关系，再利用声学在线监测技术来监测阀门在不同工况下空化程度。在工程应用上也可以用其分析调节阀的空化噪声辐射分布情况，为阀门空化噪声分析提供一定参考。

4 结语

通过CFD和LMS Virtual lab联合仿真声振耦合数值分析方法研究调节阀开度与进出口压差对空化噪声的影响，得到如下结论：

（1）调节阀空化噪声随着开度的增加呈先减小后增大的趋势，当调节阀位于小开度时，压差较大，容易产生空化，且声压级迅速增大；随着开度的增大，压差减小，声压级开始降低；当开度继续增大时，流速迅速增加，声压级也随之增大。

（2）随着调节阀进出口压差的增大，空化噪声也随之增大，在出口压力为0.45 MPa时，空化程度已经非常强烈，产生的气泡开始阻塞流道，严重时会使阀门失去调节作用，且噪声也达到93.2 dB。因此应避免调节阀在压差过大的工况下使用。

（3）通过对调节阀开度和进出口压差两种影响因素下声压级分布云图的对比分析，得到声压级的峰值出现在空化区域附近，声压级沿调节阀管阀系统呈现对称分布，符合噪声辐射的规律。

（4）可通过计算空化数来表征空化的强弱程度。不同空化程度所产生的噪声大小不同，可以建立阀门空化程度与噪声级大小的关系，将通过数值计算得到的噪声大小作为判断空化程度的依据，为用声学检测阀门空化程度的方法提供数据支持。