具有马氏切换的脉冲时滞神经网络的均方指数稳定性分析

谢小韦,印凡成

(1.南京铁道职业技术学院 社科部，南京 210031) (2.河海大学 理学院，南京 210098)

自约翰-霍普菲尔德在1982年提出了Hopfield神经网络模型,该网络模型就得到了广泛的研究关注,并在分类、模式识别、联想记忆和优化计算等方面具有广阔的应用前景．Hopfield神经网络的稳定性是该模型应用的保障和前提,因而受到大量学者的广泛关注[1-3]．

近年来,具有马尔可夫切换的神经网络受到了越来越多研究者的关注[4-6]．具有马尔可夫跳跃参数的神经网络是一个具有两个分量x(t)和r(t)的混合系统．这类神经网络以一种随机的方式从一种模态切换到另一种模态,这是由连续时间的马尔可夫链r(t)决定的．马尔可夫跳跃神经网络比确定性神经网络更为普遍和复杂．

在实践中,时间延迟、脉冲扰动可能导致神经网络不稳定和性能差．在真实的神经网络中经常遇到时滞,从而导致神经网络的振荡或不稳定,这对神经网络的应用是有害的．同时,神经网络经常受到冲动的干扰,在某些瞬间发生突变,从而改变其运动轨迹．这种现象称为脉冲．时滞脉冲神经网络的动力学行为,已有大量结果被报道[7-11]．此外，当一个系统的长时间的动力学行为时,因受到环境的扰动的影响,系统的参数将会随着时间的变化而改变．

近年来,关于具有马氏切换的脉冲/非脉冲、自治/非自治的时滞神经网络稳定性的研究：文献[3-6, 11-12]中,非自治和脉冲因素都没有被考虑；文献[1,2,7-10,13]研究脉冲神经网络的稳定性,但是忽略了非自治因素；文献[14-19]研究非自治神经网络的稳定性,但是忽视了脉冲扰动．目前具有马氏切换的非自治脉冲时滞神经网络的稳定性尚未被充分研究，因此文中研究一类具有马氏切换的脉冲时滞Hopfield神经网络指数稳定性问题，通过将经典的Razumikhin技巧和随机分析工具相结合,建立新颖的向量Halanay不等式,基于该不等式结合脉冲系统分析技巧,得到系统指数稳定性的充分条件．

1 预备知识

令R+[0,+∞],τ>0．定义PCC([-τ,0],Rn)为分段右连续函数φ:[-τ,0]到[-τ,0]映射的集合,且有‖φφ(θ)|．定义(Ω,F,{Ft}t≥0,P)为完备概率空间．定义定义为有界的、F0可测的、PC值随机变量φ,其范数定义为‖φφ(θ)|2<∞,其中E为该随机过程的期望．

考虑具有Markovian切换的非自治脉冲时滞Hopfield神经网络模型:

(1)

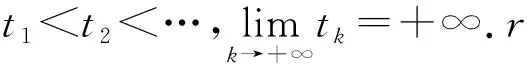
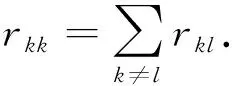
LV(x,y,t,k)=Vt(x(t),t,k)+Vx(x(t),t,k)×[-D(t,k)x+A(t,k)f(x)+

式中：

D(t,k)=diag(d1(t,k),…,dn(t,k))，

A(t,k)=(aij(t,k))n×n,B(t,k)=(bij(t,k))n×n.

假设1对一切x,y∈Rni=1,2,…,n,存在正常数Fi,使得

|fi(x)-fi(y)|≤Fi|x-y|,i,j=1,2,…,n.

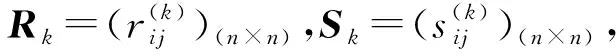
定义1系统(1)是均方指数稳定的,若存在非负整函数λ(·)以及正常数C,使得对于任何有初始条件φ∈C([-τ,0],Rn)的解x(t,φ),都有

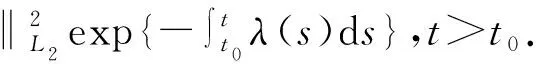
2 主要结论

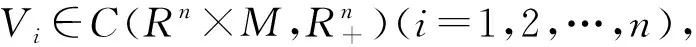
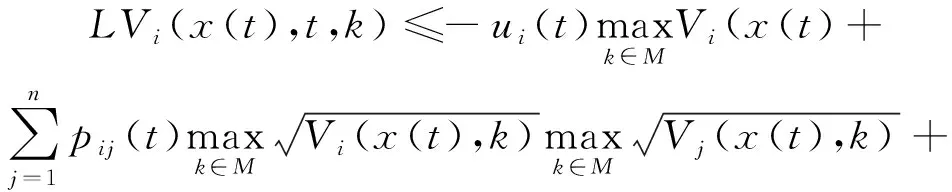
(2)

且存在正函数λ(·)使得

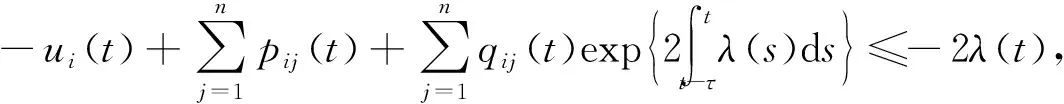
(3)

则对于任意的i=1,2,…,n有

(4)

若初始条件满足

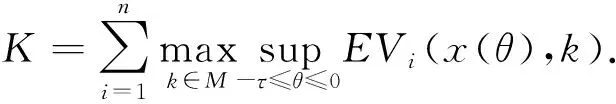
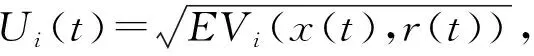
(5)

要证式(6),可先证对于任何非负常数ε,i=1,2,…,n有

t≥t0

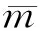
(6)

Ui(t)≤yε(t),t∈[t0-τ,t*]i=1,2,…,n

(7)

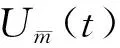
式中：D+为Dini-导数.结合条件(2)可得：

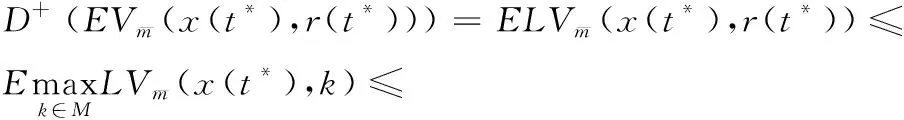
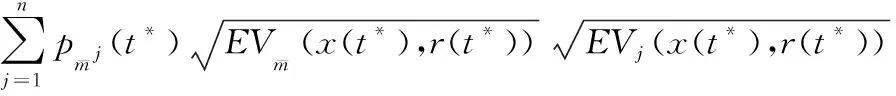
故：

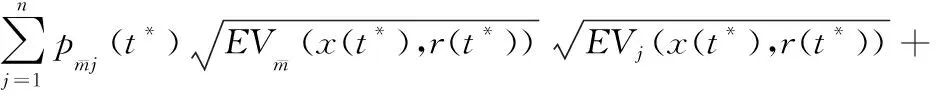
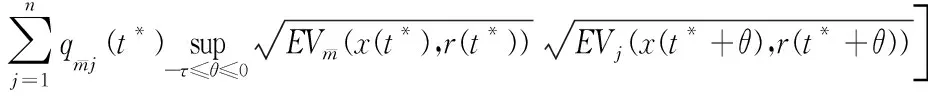
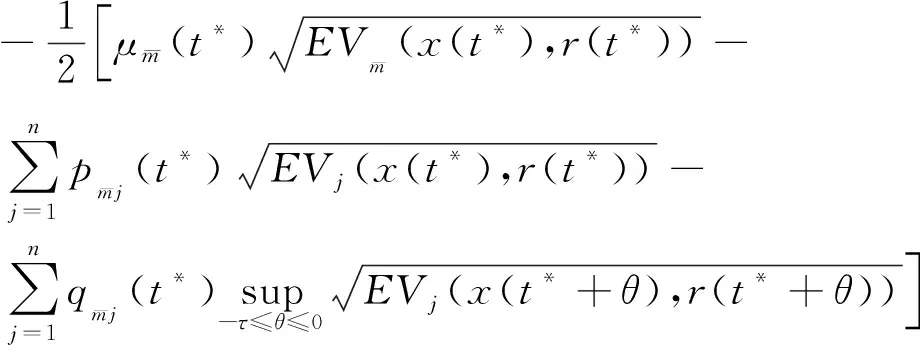
与式(7)矛盾,所以对于任意的t≥t0,式(6)成立．令ε→0,可得：

t≥t0,i=1,2,…,n

证毕．

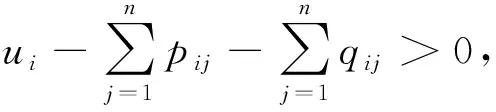
注2相对于文献[20-21],文中建立的向量Halanay不等式具有时变系数,更适合由于非自治神经网络系统的稳定性分析．

定理1假设存在正对角矩阵S(k)=diag{s1(k),s2(k),…,sn(k)},k∈M,和正函数λ(·)使得

-2λ(t)t≥t0,i=1,2,…,n

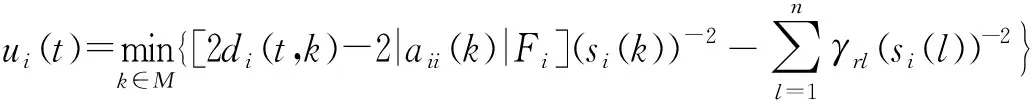
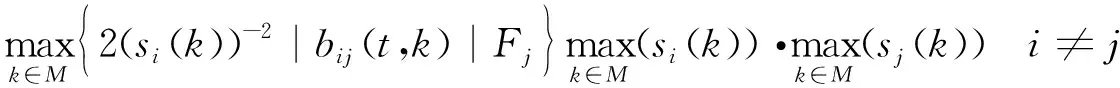
并且

式中：

则系统(1)是均方指数稳定的．

证明:对Vi(x(t),k)=(si(k))-2|xi(t)|2,i=1,2,…,n,k=1,2,…,m使用It公式,可得

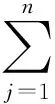
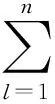
由Vi定义可得：

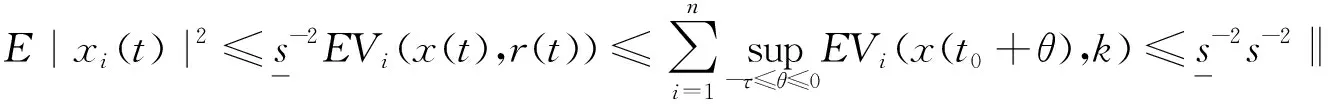
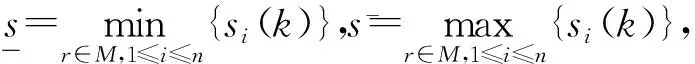
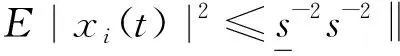
故由引理1可得：

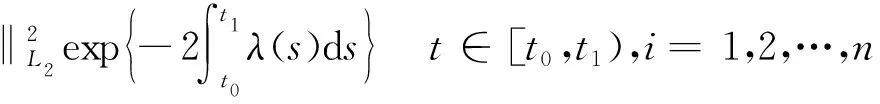
(8)

现用数学归纳法证明:

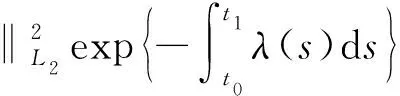
t≥t0,i=1,2,…,n

假设对于任意的s=1,2,…,k,有

E|xi(t)|2≤

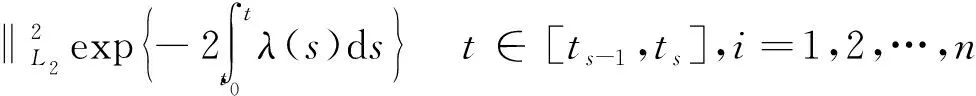
(9)

式中：δ0=1．由式(8)可知s=1时结论成立,则根据假设2有:

sik(x1((tk-τi1(tk))-),x2((tk-τi2(tk))-),…,xn((tk-τin(tk))-))]2≤

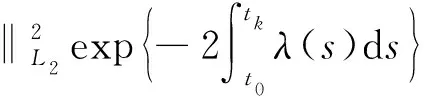
i=1,2,…,n

又由式(9)可得：

E|xi(t)|2≤

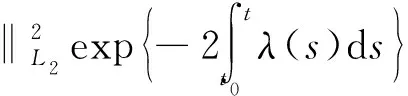
t∈[-τ,tk),i=1,2,…,n

根据引理1可得：

E|xi(t)|2≤

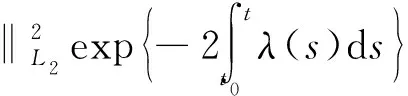
t∈[tk,tk+1),i=1,2,…,n

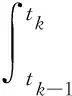
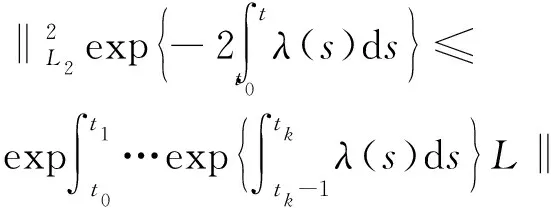
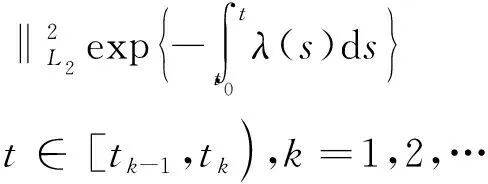
证毕．

当di(t,r(t))≡di(r(t)),aij(t,r(t))≡aij(r(t)),bij(t,r(t))≡bij(r(t)),系统退化为自治系统,则由定理1可得如下推论:

推论1假设存在正对角矩阵S(k)=diag{s1(k),s2(k),…,sn(k)},k∈M使得

并且存在一个正的常数α,使得

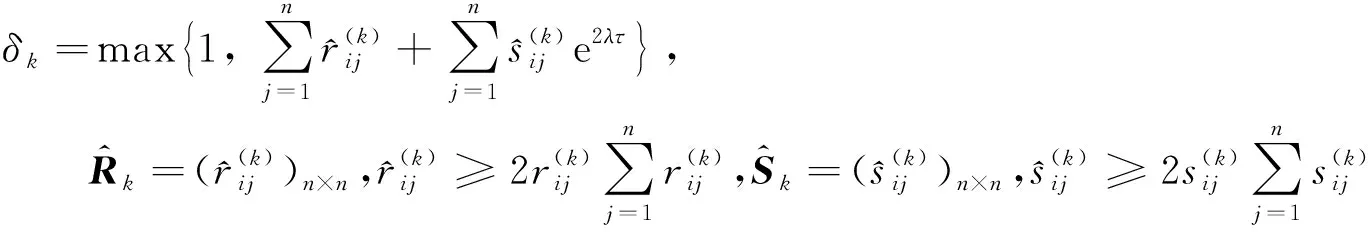
成立,则系统(1)相应的自治系统是均方指数稳定的．

当不考虑脉冲因素时,系统退化为非自治系统马氏切换神经网络,则由定理1可得如下推论:

推论2假设存在正对角矩阵S(k)=diag{s1(k),s2(k),…,sn(k)},k∈M,和正函数λ(·)使得：

式中：

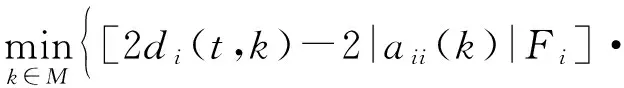
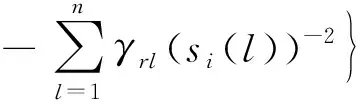
则系统(1)相应的无脉冲系统是均方指数稳定的．

注3现有文献中关于针对具马氏切换时滞脉冲神经网络的稳定性的判据是基于线性矩阵不等式方法[1,4-5,12-13]，其优点是可借助MATLAB中专有的工具箱求解,但是对系统有较强的限制:要求时滞函数的导数不超过1．文中提出的充分性判据不受这个条件限制,因而相对于文献中的判据有广泛的使用范围．

注4文献[3,22-23]基于Halanay不等式方法研究了时滞神经网络的稳定性．相对现有文献中的Halanay不等式,文中建立的Halanay不等式体现了交叉项,并和系统结构及所研究的稳定性类型有极强的契合度,避免了现有文献中因通过使用初等不等式放缩带来的保守性．

注5文中基于建立的变系数向量Halanay不等式,将处理脉冲因素和马氏切换的分析技巧有机结合,研究同时具有非自治、脉冲和马氏切换时滞神经网络的均方稳定性,建立充分性判据．相对现有文献[3,20-23],研究结果具有更大的广泛性．

3 数值例子

考虑以下模型:

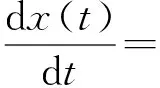
(10)

式中：f(x)=0.2x,x∈R,τ(t)=sin(t),tk-tk-1=0.3k;系统的系数为:

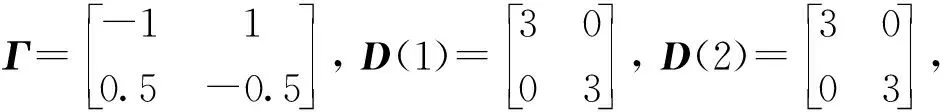
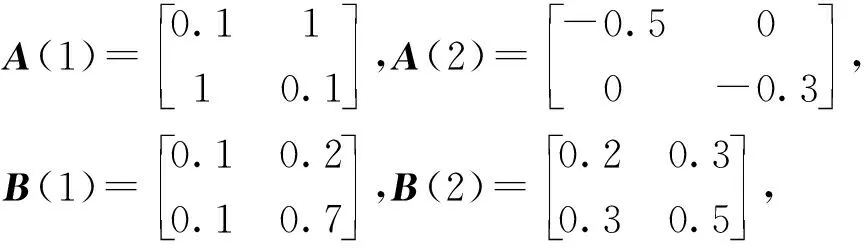
以及对k=1,2,有

r1k(x1,x2)=0.25e0.02kx1-0.05e0.02kx2,

r2k(x1,x2)=-0.25e0.02kx1+0.2e0.02kx2,

s1k(x1,x2)=0.25e0.02kx1,

s2k(x1,x2)=-0.25e0.02kx2

定理1中的参数为：

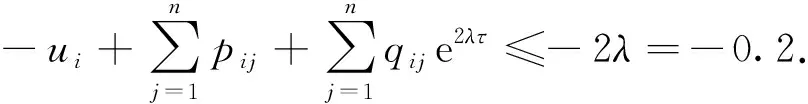
对k=1,2,简单计算易得:

定理1的所有条件被满足,系统(10)是均方指数稳定的(图1)．

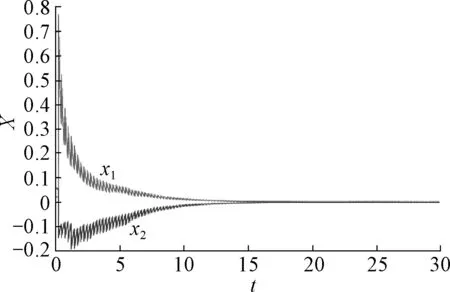
图1 系统(10)的一条轨道Fig.1 A track of system(10)

4 结论

文中研究一类具马氏的非自治脉冲时滞Hopfield神经网络的均方稳定性，得到如下结论:

(1) 通过使用新颖的技巧克服了同时考虑切换、脉冲和非自治因素带来的困难,建立了该Hopfield神经网络系统的均方稳定性的充分条件.

(2) 通过随机分析工具和Razumikhin技巧建立与所研究系统结构相兼容的向量Halanay不等式.

(3) 所得的判据具有较小的保守性,并且放宽了对时间变化率的要求．