六自由度摇摆台反解建模与仿真

梁东生,王利娟,冯兆缘

(1.江苏科技大学 镇江四洋柴油机制造有限公司, 镇江 212003) (2.江苏科技大学 能源与动力工程学院, 镇江 212003)

英国学者Stewart于1965年提出了六自由度并联运动平台的典型机构—Stewart,经过50余年的发展,该平台己成为涉及机械工程、计算机科学、软件工程、控制工程和系统仿真等多学科领域的系统集成技术[1-4]，在柔性制造,运动空间姿态模拟等领域发挥了越来越显著的作用，并由此发展出并联机构理论.由于并联平台比串联平台更具有刚度大、稳定性好、承载能力强等优点,因此，其在机器人执行器、运动模拟器、并联机床等领域得到了广泛应用[5-8]．

文献[9]基于反解算法利用MATLAB构建了6-DOF的仿真平台，并对运动平台6个作动器的位移、速度等进行计算;文献[10]在 MATLAB中利用 xPC Target 技术和模块编程的思想对6-DOF进行正解和反解，但文献[9-10]的算法均过于复杂,控制成本较高,且仿真输入数据均未与实验数据进行比较，无法验证其算法的准确性．文献[6]建立并联6-DOF平台控制系统的数据通信通道,将海浪视觉模拟系统与并联六自由度平台控制系统联系起来，该方法为在MATLAB/Simulink建立的仿真系统的数据通信提供了良好的基础．文中以液压六自由度并联摇摆实验台为研究对象,推导6-DOF平台位姿的反解方程,利用MATLAB/Simulink搭建了反解模型,分析平台在6个自由度上的运动规律,为进一步开发平台的控制器,制定可靠的策略奠定了基础．

1 6-DOF平台反解模型的构建

1.1 6-DOF平台

6-DOF平台主要包括:上平台、下平台(固定)、6个液压缸、电液伺服阀、12个球铰等关键部件．其中,液压缸通过球铰以并联方式将上下平台连接成一柔性系统,通过6个液压缸的协同运动,实现上平台在空间6个自由度方向上的姿态变化[11-13]．文中研究的实验室液压6-DOF平台主要用于模拟器在颠簸路面或海面上波浪作用下的摇摆姿态模拟,检验所模拟的驾驶模拟器运动运行的状态，液压6-DOF并联摇摆实验台如图1．

图1 液压6-DOF并联摇摆实验台Fig.1 Hydraulic 6-DOF parallel swing test bench

1.2 6-DOF平台坐标体系的建立及变换

采用坐标变换的方式对6-DOF平台的动平台(上平台)进行位置分析,其方法为:

(1) 在静平台(下平台)上建立笛卡尔静坐标系O-XYZ,坐标系原点O与静定平台上各驱动杆铰接点所在圆面的圆心重合．

(2) 在动平台上建立动坐标系O′-X′Y′Z′,坐标原点O′与上平台各驱动杆铰接点所在圆面的圆心重合．当6-DOF平台处于初始状态时,上述两个坐标系的X、Y、Z轴的方向一致,Z-Z′轴重合,X-X′与Y-Y′相互平行,如图2．由Z轴方向投影,可得到上、下平台铰链点的分布,如图3．

图2 平台坐标系Fig.2 Platform coordinate system

图3 上、下平台铰链点Fig.3 Upper and lower platform hinge points

6-DOF平台的参数如表1．

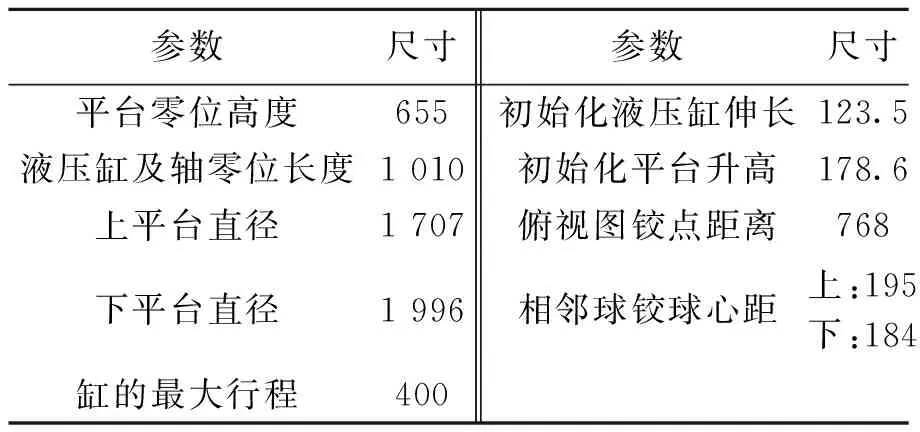
表1 6-DOF平台参数

将6-DOF平台参数代入图2的平台坐标系中，得到平台处于零位状态时各铰点的坐标,如表2．

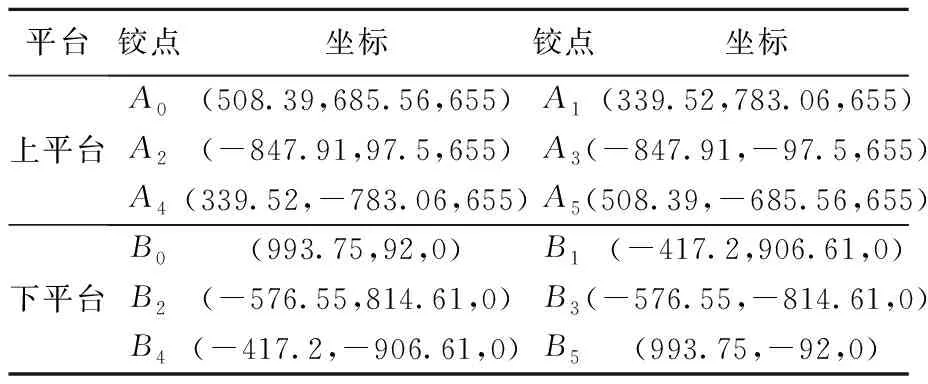
表2 上、下平台各铰点零位坐标

由6-DOF平台中上平台在空间中的姿态可求各液压缸的伸缩长度,即位置反解．对其进行反解,将动坐标系中铰链点的坐标向量变换到静坐标系中,再将变换得到的向量与静坐标系中铰链点的坐标向量相减得到液压缸的缸长矢量,从而求出缸长[14-15]．

采用欧拉角方式来描述动坐标系在静态坐标系中的姿态,对6-DOF平台运动姿态分析,通过3次平移变换,将静坐标系分别沿着X轴、Y轴、Z轴进行平移运动；再进行3次旋转变换,即沿X轴、Y轴、Z轴旋转．通过以上过程,可得到由静坐标系到动坐标系的坐标变换矩阵T=

(1)

1.3 6-DOF平台位置反解

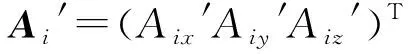
当平台动作时,上下相应铰支点间距离li的计算公式为:

(i=1,2,…,6)

(2)

Δli=li-l0

(3)

式中：Δli为液压缸缸长的伸缩量,l0为液压缸的初始长度.

2 6-DOF的运动学反解仿真

利用MATLAB中的Simulink模块建立了6-DOF平台反解仿真模型,如图4．模型包括期望信号输入模块、液压缸缸长反解算法模块、信号输出模块．将文中所提的6-DOF液压缸缸长反解算法以MATLAB Function模块写入整个仿真模型中,得到各液压缸的长度变化规律．

图4 6-DOF台运动学反解Simulink仿真模型Fig.4 Kinematics inverse solution of 6-DOFSimulink simulation model

让6-DOF平台分别仿真沿X轴平移、沿Y轴平移、沿Z轴平移、绕Z轴旋转运动,其中平移幅值为100 mm,频率为1 Hz,转动的幅值为π/6, 频率为1 Hz．通过反解算法模块得到6个液压缸缸长变化规律,用示波器Scope 模块,将缸长变化量以图像的形式输出．仿真时6个自由度的运动均为正弦运动,仿真结果见图5,图中曲线1～6代表1～6号液压缸．

图5 液压缸长度变化曲线Fig.5 Hydraulic cylinder length variation

图5直观地反映了6-DOF平台位姿变化时,6个液压缸缸长变化规律．所建仿真模型简单方便,为进一步研究6-DOF平台并能更好地完善其控制策略奠定基础．

将实验室中6-DOF并联摇摆实验台沿X轴的平移运动,得到各液压缸缸长实际值如图6，验证所建6-DOF平台反解算法及所建仿真模型的正确性．

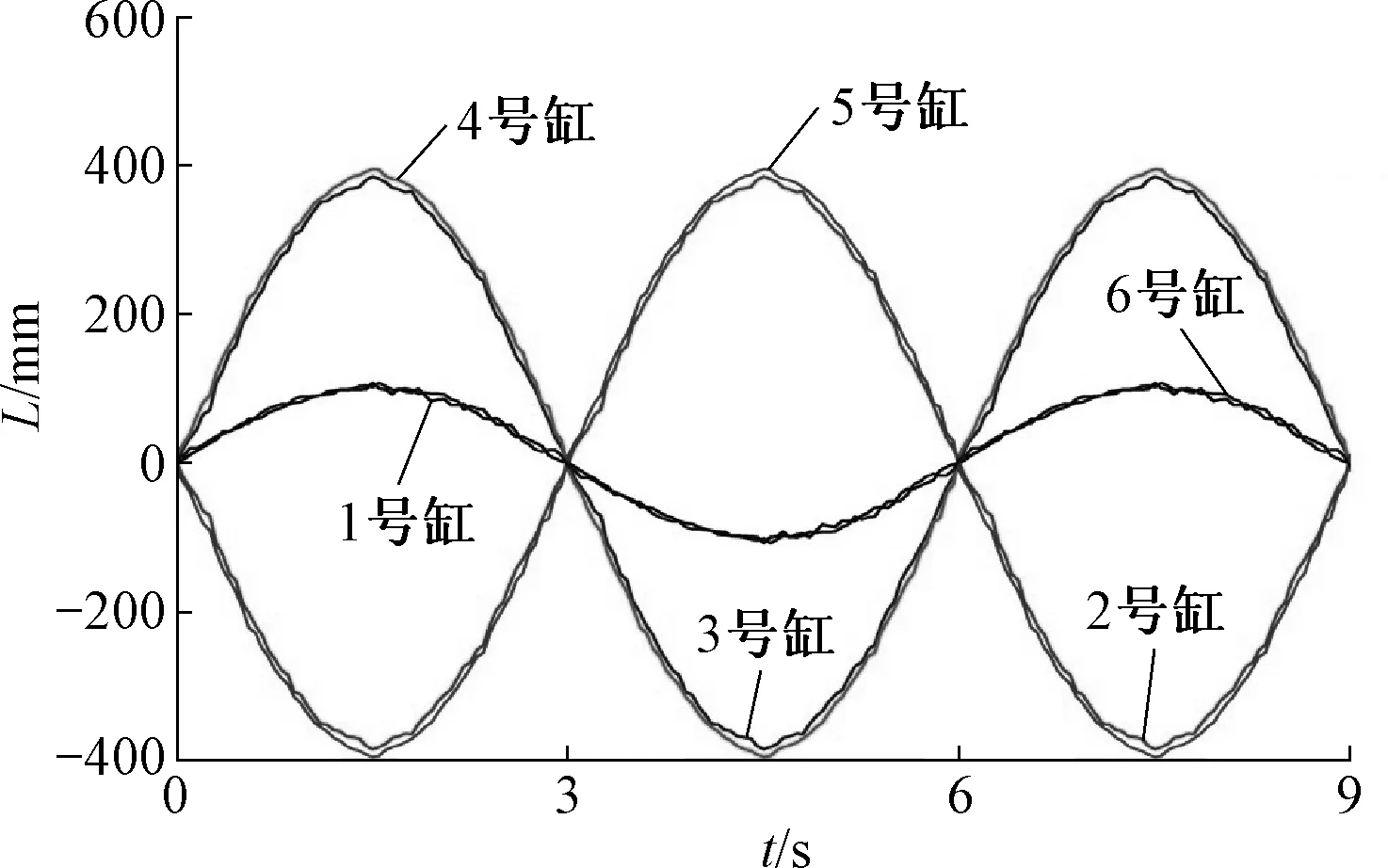
图6 沿X轴平移时液压缸缸长实际值Fig.6 Actual cylinder length when movingalong the X-axis

3 结论

(1) 通过建立6-DOF平台坐标及其换体系,推导6-DOF平台的反解算法,利用MATLAB中Simulink模块建立了6-DOF平台的仿真系统,直观地得到了各液压缸缸长变化规律,反解算法简便,仿真系统简单高效．

(2) 采用6-DOF平台仿真系统与试验台研究姿态变化运动,得到各液压缸缸长变化规律,验证反解算法及仿真模型的正确性,6-DOF平台的运动规律,为下一步深入研究6-DOF平台运动特性及其控制系统打下良好的基础．