基于粒子群算法的多Kinect校准

吴泽烨，田建曌，车武军，3

(1.中国科学院 自动化研究所，北京 100190；2.中国科学院大学 计算机与控制学院，北京 100049；3.北京未来影像高精尖创新中心，北京 100088)

1 引言

动作捕捉技术在游戏设计、动画、运动分析、虚拟现实等应用中有广泛的应用。动作捕捉技术主要分为基于标记点的方法和无标记点的方法。前者虽然采样精度高，但是系统整体造价高昂、操作复杂。无标记点的方法通过处理RGB相机或深度相机的数据来捕捉人物的动作。随着廉价的深度传感设备的普及，利用深度数据进行人体运动捕捉的技术受到学术研究与产业应用人员的共同关注。

使用单台深度相机进行动作捕捉[1，2]主要限制在于人物的遮挡。当前的一些算法虽然可以实现在人体发生遮挡之后重新出现时继续对其跟踪，但是这些算法对于在人体被遮挡期间的骨架信息仍然无法完整获取。而使用多台深度相机组成的系统[3-5]，可以提供一个更大的视野范围。Kinect v2是一款典型的TOF深度相机，配套SDK包含人体姿态跟踪、人脸识别等功能，但其性能当前与专业的设备相比还存在很大差距，SDK中提供的基于机器学习的骨架跟踪方法[6]捕捉速度快、计算量小，但捕捉结果严重依赖于学习样本，对正对设备的人体识别效果较好，而对自遮挡、复杂的人体姿势如蹲坐等识别效果较差，且不能分辨人体的正背面。因此，通过多个Kinect的传感数据融合来提高系统性能具有重要的研究意义。不同Kinect使用自身的坐标系定义数据，对来自不同Kinect的人体目标数据处理时，必须采取一定方法将多个Kinect视角下的数据校准到同一坐标系下，这样才能对数据进一步融合处理。目前标定kinect深度相机外参数主要有两种方法[7，8]。一是类似标定彩色相机，对棋盘格采集红外灰度图像，采用张氏标定法，但这种方法假设红外深度相机在生成红外图像与深度图像时的坐标系完全重合[9]，操作较为繁琐。Núez 等人[4]则是标定彩色相机的外参数用以代替深度相机外参数。二是为棋盘格设计具有深度特征的孔洞，从而用于标定深度相机，但空洞边缘的点可能会丢失，因此精度有所损失[10]。另外，Wei等人[11]提出KSCC校准算法，用于校准在远程训练系统中的任意位置的使用者的动作数据，该方法首先收集远程使用者的骨架数据，并利用该数据计算使用者与Kinect的相对位置，将不同初始位置的使用者坐标校正到同一个坐标系下。但KSCC算法有一定的限制，要求Kinect相机高度一致且朝向为水平。本文基于Kinect捕捉系统的特点，在KSCC算法基础上进行改进，提出了一种校准多个Kinect设备的人体数据的方法，使得操作更加简便灵活，无需辅助标定设备或严格摆放相机。

2 系统概览

校准系统总体结构如图 1所示：每个Kinect作为客户端，通过TCP通讯协议与服务器端相连接，在服务器端收集总体数据并计算校准参数。

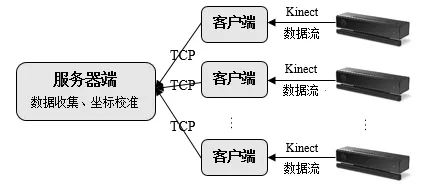
图1 系统结构

校准方法的流程如下：

a)系统收集静止站立使用者的骨架数据；

b)对每个Kinect，使用累积的数据计算平均骨架与骨架的中心点坐标；

c)设置某个Kinect的坐标系为系统世界坐标系；

d)使用粒子群优化算法计算出每个Kinect对应的刚体变换矩阵。

此后系统就可以利用该矩阵将捕获的人体数据如骨架坐标、点云数据等变换到统一的世界坐标系下，进行进一步的数据融合处理。

3 算法描述

3.1 骨架数据获取与计算

系统采集数据时，使用者站立在Kinect的有效数据采集重叠区域，人体在每个Kinect的视角中都不发生外部遮挡。Kinect SDK中一个人体骨架由25个关节点组成，每个关节点对应一个跟踪状态，则第i台Kinect中目标人物骨架的第j(1≤j≤25)个关节点坐标可表示为，vij=vij(x，y，z)关节点权重记为wij，与关节点跟踪状态Stateij有关，根据实验将wij取值如下：

当服务器对每个Kinect分别收集N帧数据后，开始计算平均骨架。一般N约为20至30，Kinect设备刷新帧率为30，则数据收集在一秒内结束。对于第i台Kinect，其中目标人物骨架的第j个关节点在N帧中坐标的加权和Sij为：

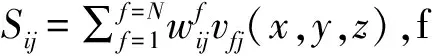
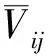
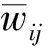
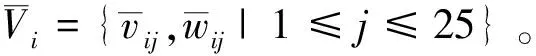
另外，由于Kinect根据深度信息追踪人体骨架时，无法确定用户是否正对设备，当用户背对Kinect摄像头时，其提供的骨架坐标是左右反转的。为此设定一个简易的初始姿势(如右手举起)辅助系统判断骨架的左右。计算出每台设备的加权平均骨架后，服务器利用姿势检测判断骨架正反面，并依此更新平均骨架。

3.2 求解刚体变换

服务器选择信息可信度最高(即加权骨架关节点权重和最高)的Kinect作为参考，其坐标系设为世界坐标系。对其他Kinect的平均骨架关节点做刚体变换，变换到参考Kinect的坐标系下。

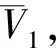
(1)

记任一非参考Kinect的最优刚体变换矩阵为M，则M含有6个自由度(3个旋转自由度、3个平移自由度)，变换矩阵M可由4*4矩阵简化为由(θx，θy，θz，tx，ty，tz)表示的数组，其中θx、θy、θz分别为骨架绕x，y，z坐标轴旋转的欧拉角，tx、ty、tz分别为骨架沿x，y，z坐标轴平移的距离。此时可利用最小优化算法找到使得F值最小的(θx、θy、θz，tx，ty，tz)，得到旋转变换矩阵R(θx、θy、θz)=Rz(θz)·Ry(θy)·Rx(θx)，由三个平移变量tx、ty、tz得出平移矩阵T(tx，ty，tz)，从而计算出变换矩阵为M(θx，θy，θz，x，y，z)=T(tx，ty，tz)·R(θx，θy，θz)。

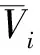
3.3 粒子群优化算法

对每个非参考Kinect，本文采用粒子群优化算法来求解使式(1)最小的变换矩阵，将该非参考Kinect的中心位置坐标与参考Kinect的中心坐标差值作为偏移量初始值中心进行随机初始化。具体算法过程如下：

1.初始化：

设置粒子群规模，初始化所有粒子，包括随机位置和随机速度；

2.迭代过程：

a)计算每个粒子p的适应值：

b)将每个粒子的计算出的适应值与该粒子历史最优值pbestp比较，如果计算得出的适应值小于历史最优值，则用当前位置替换历史最优位置；

c)找出粒子群中所有粒子的适应值最小值，与整个粒子群的历史最优值gbest作比较，如果比历史最优值小则用当前位置替换历史最优值；

d)更新每个粒子p的速度：

其中ω为粒子惯性参数，c1、c2为粒子的“学习”速度权重，r1、r2为介于0与1之间的随机数；

f)当最大迭代次数达到k次，或全局最优适应值连续φ次稳定在一个值附近时，达到迭代结束条件，否则转跳到计算粒子适应值的步骤继续寻找最优解。

粒子群优化中的全局最优适应值即为最优F值的近似。如果收敛后的适应值较大，说明校准结果精度较差，需要重新收集数据进行校准。

4 实验结果

为验证本文算法的有效性，进行如下实验：固定一台Kinect，将另一台Kinect摆放在3个不同的位置，分别进行10次校准，每次校准时对每台Kinect分别收集30帧骨架数据。

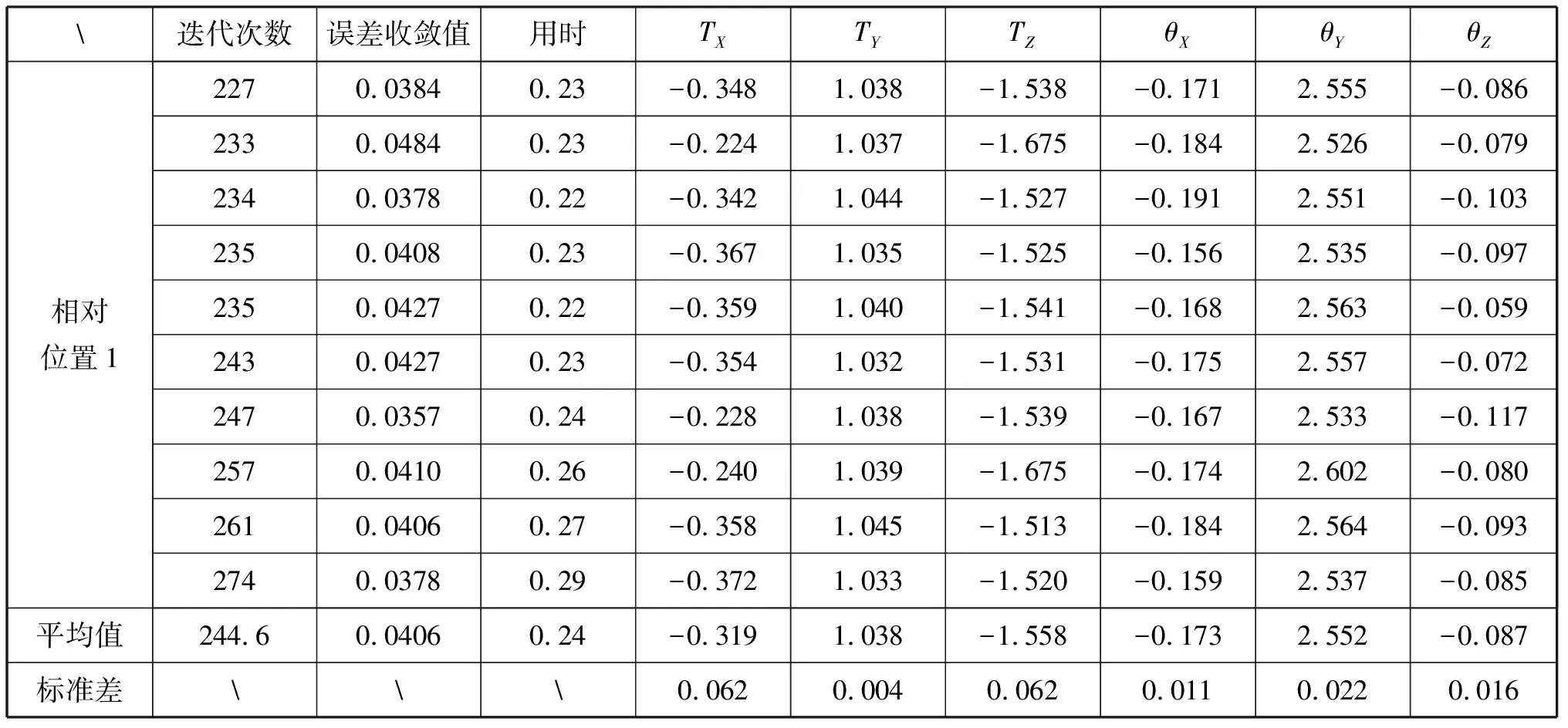
表1展示了30次校准实验的结果，可以看到误差收敛值一般低于0.08m，平移参数tx的标准差在0.04m左右，ty、tz的标准差在0.01m左右，欧拉角的角度误差约在1.2°左右。因此本校准算法的结果较为稳定，准确。图2为一次实验中两台Kinect坐标系校准前后的追踪数据，将同一人在两台Kinect下捕捉到的人体数据变换到校准的世界坐标系下，图中显示变换后的两个人体骨架基本重合，点云数据也能很好地融合。

实验中，校准算法单线程运行于主频3G的CPU，每次校准一台非参考Kinect所需迭代次数平均为240次，最多为274次，用时平均为0.24秒，最多不超过0.3秒。用4台Kinect就可较好地覆盖人体运动的360°视角范围，而4台Kinect所需要的校准时间约为1秒，故本校准算法运行效率较高，具有实用性。

本文算法基于Kinect的跟踪结果进行校准，当Kinect本身跟踪骨架误差过大时，校准平均误差也会随之增大，导致校准失败，需重新收集数据校准。因此初始累积数据时，需保证使用者在Kinect的合适捕捉范围内。

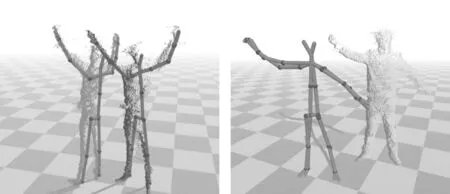
图2 两台Kinect校准前(左)、校准后(右)人体数据

迭代次数误差收敛值用时TXTYTZθXθYθZ相对位置12270.03840.23-0.3481.038-1.538-0.1712.555-0.0862330.04840.23-0.2241.037-1.675-0.1842.526-0.0792340.03780.22-0.3421.044-1.527-0.1912.551-0.1032350.04080.23-0.3671.035-1.525-0.1562.535-0.0972350.04270.22-0.3591.040-1.541-0.1682.563-0.0592430.04270.23-0.3541.032-1.531-0.1752.557-0.0722470.03570.24-0.2281.038-1.539-0.1672.533-0.1172570.04100.26-0.2401.039-1.675-0.1742.602-0.0802610.04060.27-0.3581.045-1.513-0.1842.564-0.0932740.03780.29-0.3721.033-1.520-0.1592.537-0.085平均值244.60.04060.24-0.3191.038-1.558-0.1732.552-0.087标准差\.0620.0040.0620.0110.0220.016

注：表1在3个相对位置各进行10次校准实验的结果。从左至右的参数列分别为迭代次数，误差收敛值(m)，用时(s)，平移参数tx、ty、tz(m)，旋转参数、Qx、Qy、Qz(rad)

5 结束语

本文提出了一种校准多Kinect人体数据的算法，基于单Kinect捕捉系统来校准多个Kinect的人体数据，为后期的数据融合提供方便。本算法具有以下优势：

1)操作简单。不需要辅助的标定物体，而是基于Kinect本身提供的骨架数据进行校准，对Kinect的摆放与使用者的相对位置姿态无严格要求；

2)基于粒子群算法优化，校准速度快，精确度较高；

3)可扩展性好。对于利用单个深度传感器进行跟踪识别的系统，均可使用本文算法框架，从而利用多个传感器提供的更广泛的范围、通过数据融合提升系统表现。

另外，本算法也可以简单地扩展为多次校准，即获取人体在不同位置的多个骨架信息，减少系统噪音的影响，以取得更好的校准精度。但是，受限于原始数据的准确度，现实环境的复杂等，本文算法也有一些局限性，如当Kinect设备提供的骨架位置信息误差过大时需重新收集初始数据等，在下一步工作中将重点解决这些问题。