房地产调控政策下北京市住宅价格预测
2018-02-15郭峻言张辉
郭峻言,张辉
(中国传媒大学,数据科学与智能媒体学院,北京 100024)
1 引言
1.1 研究背景
近年来,为了保障房地产行业的健康发展,为了避免房价过快增长以及过度波动对人民生活产生影响,我国各地出台了系列的房地产调控政策,产生了一定的效果,以北京为例,北京市从2010年4月30日出台“京十二条”正式拉开了房地产调控的序幕,随后,北京陆续出台了一系列的房地产调控政策,2017年3月,为了贯彻习近平总书记关于“房住不炒”的要求,遏制北京住房从“住”到“炒”转化的现象,北京市出台了“最严限购令”,主要内容包括住房首付比例提高、非京籍纳税要求变严、银行贷款门槛提升等。北京市住房价格2003年、2008年住房价格出现了重大拐点(激增、跌落),2009年在政策背景下回升并在后续年份中趋于稳定,由此可以发现,房地产政策的出台及其挥作用,使得住宅价格产生波动。
1.2 相关研究
近年来对于房价的研究角度愈发多元,学者们也不断尝试利用新的研究方法,利用新的模型对于房价的演变做出解释和预测。
在关于北京房价的影响因素方面,韦靓(2012)在提出,北京房地产市场是一个很复杂的市场,其波动受到包括国内金融市场在内的多个因素的制约。关海玲(2015)进一步提出北京市房地产价格波动受到宏观经济因素、首都战略政策因素、土地市场供求因素和房地产假设投资因素影响。
在关于房价的预测方面,国内研究者的研究方法多集中于灰度系统GM(1,1)(王莹(2017)等)、ARMA模型(曹阳(2017)等)以及BP神经网络预测。研究普遍对政策影响与预测模型修正思路少有涉及,政策量化仍为待探索领域。
从限购政策本质出发,王敏、黄滢(2013)构建了动态模型,发现限购政策对于房价降低影响不大,市场表现出“价高量低地”的情况;安辉、王瑞东(2013)发现房地产调控政策对房地产价格具有重要影响作用;黄振宇认为中国土地出让制度和税费制度缺陷是住宅价格快速上涨的基础原因;余华义(2010)也认为中国房价受政策影响较大。李晓曼(2017)通过实证检验证明,影响房地产价格的两个重要因素一是限购政策,另一个是公积金政策,并认为,开展政策调控时,在短期内,住宅价格为出现下降,但当调控放松时,政策对房价的抑制作用减弱。
1.3 研究方法
北京市住宅价格从数字特征出发包含着一定的长期规律,使用与长期记忆规律和体现方差效应的函数组进行处理。本文利用时间序列的全距和标准差的关系建立统计量Qn:
(1)
其中,Rn是样本区间累计离差的极差,Sn为样本的标准差。Rn的计算过程中,首先要定义第j个区间的离差,并计算离差和的极差:
(2)
Hurst指数采用最小二乘法:
log(R/S)=log(c)+H×log(n)
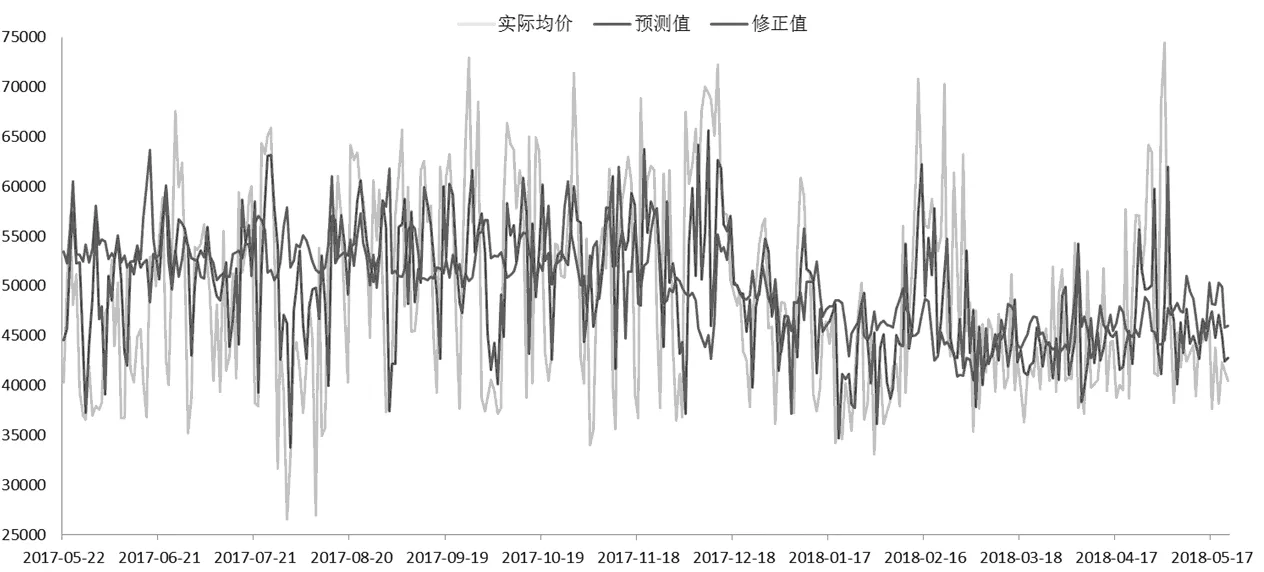
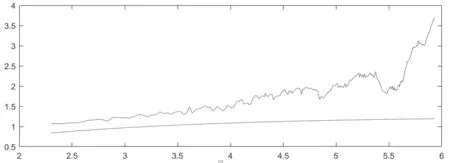
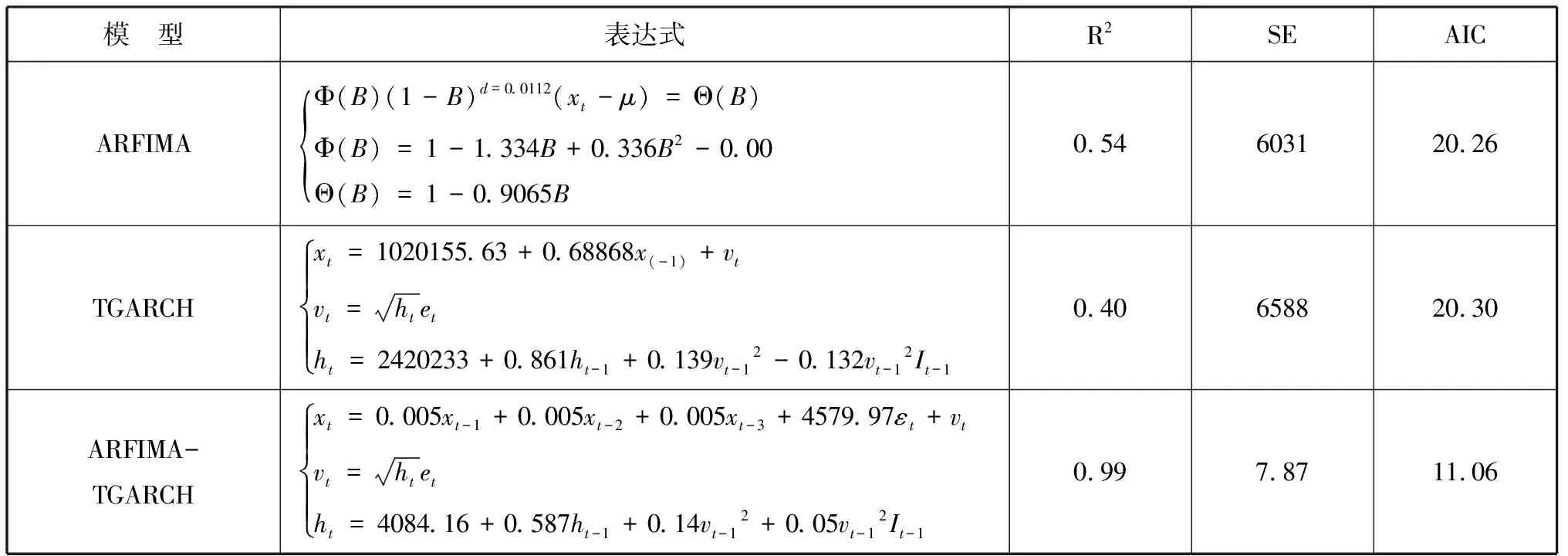
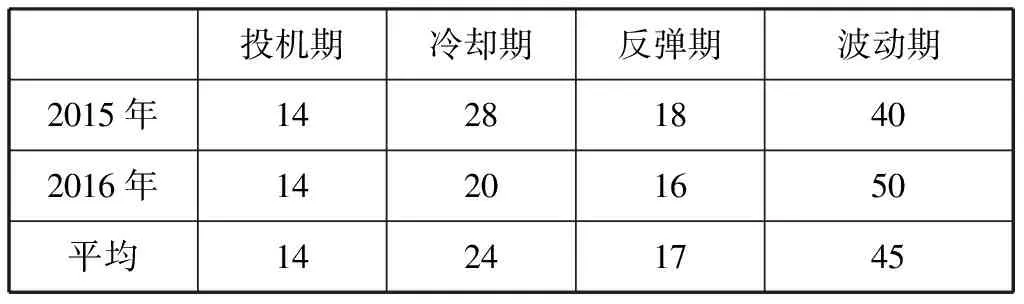
当H=0.5时,时间序列可用随机游走表述,当0.5 (3) ARFIMA模型在处理具有长记忆性的时间序列数据时,效果优于仅基于长记忆的差分模型和ARMA模型的单独使用。 当时间序列具有ARCH效应时,方差波动将对模型产生影响。GARCH模型族将出现异方差效应的时间序列模型的残差的方差进行拟合。GARCH模型本身存在着一定的不足:条件严格,异方差拟合参数必须非负;条件方差平稳,参数有界,且残差平方参数和与异方差函数参数和之和需小于1;正负扰动对称,残差平方和的系数不能影响未来预期,且效应出现较慢,信息存在严重的不对称性,影响预测和拟合精度。TGARCH模型可解决这种不对成性,其公式为: (4) 其中,It-1为虚拟变量,当εt-1<0时,示性函数=1,否则为0。即在正干扰下的影响为β,负干扰影响为β+γ,γ>0,则杠杆效应存在。EGARCH模型实质是进行了指数变化,根据陈鹏和李星野的研究,两种模型拟合效果几乎一样,TGARCH甚至效果更佳,本文将选用TGARCH模型。 结合ARFIMA模型与TGARCH模型,既包含了房价数字特征所包含的数字规律,也考虑了外界环境变化所导致的数据局部方差的变化。ARFIMA-TGARCH模型族可表示为: (5) 本文选取网易房产北京住宅销售日度数据进行研究。为量化2017年3月17日起发布的系列限购政策对北京市住房销售数量的影响,对政策未实施阶段与政策实施后阶段售房数量与均价数据进行独立正态性检验(Shapiro-Wilk检验)。经检验,Shapiro-Wilk检验的p值为0.0008和0.0001,小于置信度α=0.05,数据不符合正态分布,故拒绝原假设。因此采用非参数方法Wilcoxon符号秩检验对政策未实施阶段与政策实施后阶段售房数量与均价数据是否有显著变化进行检验。 表1 Shapiro-Wilk检验与Wilcoxon符号秩检验 经Wilcoxon符号秩检验,政策公布前后1个月内住宅均价与售房数量总体上出现变化的p值分别为0.7204和0.6343,由于均大于置信度α=0.05,所以不能拒绝原假设,即为政策在1个月内起到了显著影响。从简单统计量出发,4月售房均价为45886元,比之3月上涨了7.2%,说明可能存在一定延后性。 由于整体指标未见显著差异,所以初步可得出以限购政策推出时间为分界对于1个月及以上周期(小于2个月)的房地产行业无显著影响的结论。以4月30日为分界,5月份房价均值为43746.73元,环比下降5.07%,5月份日售房数量均值为81.77套,环比下降10.96%。 由此可见,将时间分界线改变后,所得结论出现较大差异,说明政策的实际影响有一定的滞后性。从量化分析结果出发,2017年3月推行的系列限购政策在这一分界线上的宏观层面有一定效果,该效果在4月底最为显著。 以北京市月售房均价(P)为因变量,供给量(S)为自变量进行线性回归,所得R2值为0.899,方程显著性为0.015,两个变量间线性关系显著,经残差分析,残差项在95%置信水平满足同方差,所得回归方程为: (6) 对北京市月售房均量与供给量做相关分析,Person分析所得关系值为0.237,双尾检验显著度为0.459,因此北京售房均量与供给量不满足线性关系。调整关系,因变量为北京市月售房数量(N),自变量改为供给量(S),通过Cubic回归,所得R2值为0.791,F值为10.074大于F0.05(1,10)=4.96,回归关系显著。 2016年10月数据属于极端特殊数据,若排除该数据则可认为北京市月售房均量与供给量满足线性关系,该方程为: (7) 从数据可发现通过改变北京市房屋供给量的确能够分别对月售房均价与月售房均量造成负向和正向的影响(同一需求量,供给增加,价格下跌;同一需求量,在平衡数量以内,供给量增加,实际销售量增加),但不能得出北京市房地产行业数据波动符合市场经济规律的结论,仍需进一步进行因果检验。 量化结果表明:在限购政策出台的滞后周期内,房地产行业出现部分房产抛售,价格骤升现象,在政策正式生效后,供应量减少,整个市场处于观望状态。而从这个状态观望,在未来的半年内,房价会有局部降低,宏观稳定,但若无法达到供销平衡,在后半期会有骤然上升状态,这是对政策调控房地产行业市场的一次市场反弹。 本部分使用的数据来源于网易房产数据中心,时间段为2015年5月1日至2017年5月21日,数据内容为北京市住宅销售价格的日度数据,共752条,其中54条为0(当天无成交),但不能说明房产在该日的实际价格为0,因此采用5期移动平均法对未售数据进行拟合。对获取的房价数据除以该月CPI处理,消除物价水平因素。 对R(离差极差)与S(样本标准差)进行测算后,取对数处理,并通过最小二乘线性拟合,计算Hurst指数。图1中红线展示了拟合函数logRS=C+H×logn,其中斜率为Hurst指数=0.5112,蓝线为logn的趋势,可看出,曲线约在logn=4.8的时候出现拐点,周期数约为exp(4.8)=122天。 ARFIMA模型d值等于0.5112-0.5=0.0112,通过Grangery与Joyeux的长记忆研究中的差分迭代模型,得到新的适合ARFIMA模型拟合的数据序列。通过拟合,ARFIMA((1,2,3),0. 01,1)与ARFIMA((1,2),0,(1,2))各级指标完全相同,随机选用前一模型进行拟合。通过进一步检验,ARCH效应显著。经计算,相关诊断系数如表2所示。 图1 Logn~LogRS图像 表2 三种模型下的最优表达式与系数 横向比较三种模型(其中式一所给出的形式仅为清晰结构,变形后可继续运算),ARFIMA-TGARCH模型族的拟合效果最佳,更适合用于描述房价走势,ARFIMA模型拟合效果一般,TGARCH模型的拟合效果不佳。考虑到A-T模型族由于计入了政策、经济等环境因素导致的方差波动,因此在政策(周期)等环境发生较大变化时,ARFIMA模型的迁移效果更优,在后续预测中采用ARFIMA((1,2,3),0.01,1)模型。 由于政策影响的存在,该模型下仅能模拟2017年5月前政策环境下的房价走势(包含了2015年9月银行房贷利率下降、2016年9月房贷政策、2017年3月限购政策等大型政策),而缺失了很多未来环境中可能承载的信息量。 北京市各政策周期内数据走势和变动有一定的规律性,然而区别于季节因子的提取,不同的政策周期对于季节因子的提取特征是有差异的,因此需要寻求一个在普适的基础上,更能贴合个例所处环境特征的模型拟合规律。以较大政策环境变化制定为时间节点,本文主要以2015年7月房贷利率下调,10%上浮、2016年提升外地居民首付比例及限制购买数量,2017年3月提升本地居民首付比例等为三个研究案例,结合数字特征,重大政策拐点间的住宅价格变化可以归结为一个政策“潮汐”周期。 假设各时期于周期内分布具有一致性,所研究政策周期内时间分布。 图2 北京限购政策效用“潮汐周期现象” 投机期冷却期反弹期波动期2015年142818402016年14201650平均14241745 2017年3月起,截至2017年5月22日,已经历40天的投机期,与50天的冷却期,后续时间段为修正对象,假设下一轮限购或购房贷款等政策发布日期为2018年3月31日,由经验政策周期分布,此轮周期内,投机期为40天、冷却期为69天、波动期为128天。根据潮汐现象,我们拟构造一个修正因子Ω,形如: (8) Ω的含义是政策周期内每个时期价格变化的趋势(当期与上一期价格变化值的比值),我们认为ARFIMA((1,2,3),0,1)模型拟合的结果缺少信息量,真实的预测结果应在ARFIMA预测结果基础上乘以Ω,实现对总体趋势结果的修正。Ω>1,说明该时期内,住宅价格有增长的趋势,限购政策取得了相反的预期效果;Ω<1,说明该时期内,住宅价格有下降的趋势,限购政策能够在一定程度上取得预期效果。 根据对2015年、2016年4个时期的测算,Ω的变化趋势总体相似,值域范围有所不同,以反弹期为例,2015年值域范围为1至1.5,而2016年约为1至1.25,值域范围的缩小与市场的可变性相关(合格购买力等),政策的紧缩会导致市场可变性的降低,波动期与反弹期出现了相似的变化。而投机期,Ω值的变化相对重合,冷却期值域变化相对重合。根据政策紧缩的情况,对2017年四阶段Ω值进行经验拟合,于投资期使用0.9至1的线性拟合,冷却期使用“左偏”的0.9-1.2-1的拟合函数,反弹期生成1.05-1.25-1.2的函数并通过正态随机数进行随机变化差值,波动期生成常数值与2016年相同的三角函数。 假设2018年3月再次提出住宅购买政策,“合格购买力”水平进一步降低,各阶段的抑制性增强,且假设金融机构贷款获得能力降低10%,根据对房价波动的格兰杰因果检验,房价也将受到抑制。在以上的修正下,对2017年5月-2018年5月预测数据的修正结果如图3所示。 由图像可看出,经政策潮汐修正的北京房价随时间变化曲线相较于ARFIMA模型的预测,更加贴合实际房价波动情况,总体误差平方和减少近30%(28.63%),尤其是在反弹期的反映上,有明显的提升。 本文通过研究发现调控政策对北京市住房销售、供应以及价格的影响均具有滞后现象,同时调控政策的影响表现出“潮汐周期”现象。根据这一成果,提出以下建议。 图3 北京房价预测修正结果 (1)建立房地产调控政策的长效机制。从研究成果我们可以发现,房地产调控政策对住宅的影响具有“潮汐周期”,这必然引起住宅的波动,因此,要充分考虑特定政策可能的影响周期,充分考虑住房调控政策的长期有效性,建立长效机制。 (2)加强调控政策的科学性。过度干预会对市场造成新一轮的冲击,可能会出现市场供应出现停滞、住房租赁市场价格上涨、住宅规划土地流拍等现象。因此,政策制定过程中,应充分兼顾市场与调控的双重作用,保证调控政策的科学性、合理性。2 北京市住房供求分析
2.1 政策对北京住宅销售的影响

2.2 北京住宅供求探究
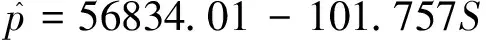

3 调控政策对北京住宅价格影响情况的研究
3.1 调控政策下北京住房价格波动预测
3.2 调控政策影响的“潮汐”现象

4 结论与建议